Prolog m Prolog concretiza o modelo de computao

Prolog m Prolog concretiza o modelo de computação abstracto da Programação em Lógica m escolher o golo mais à esquerda na resolvente (em vez da escolha não determinística da cláusula a usar na próxima redução) pesquisa sequencial das cláusulas em busca de unificação, acompanhada de retrocesso equivale a uma pesquisa em profundidade da árvore de pesquisa implementável por uma máquina de stack, onde se guardam os golos da resolvente 1

Paralelismo m outras opções no tratamento do não determinismo percorrer em paralelo todos os ramos da árvore de pesquisa (paralelismo ou nas várias alternativas de uma cláusula) p ¬ q 1, q 2 p ¬ q 3, q 4 p ¬ q 5 p q 1, q 2 q 3, q 4 q 5 executar em paralelo os vários golos de uma resolvente (paralelismo e) p p ¬ q 1(X), q 2(X), q 3 q 1(X) ou q 2(X) q 3 e Parlog, Concurrent Prolog, GHC 2

Retrocesso (backtracking) m um traço de uma computação pode continuar depois de uma falha m um f seguido a um golo significa golo falhado o golo seguinte é o que seria escolhido pelo mecanismo de retrocesso corresponde à chamada mais próxima em cujo procedimento existe uma cláusula alternativa a seguir às cláusulas já usadas o novo golo é idêntico e tem as mesmas variáveis que uma sua anterior ocorrência no traço, ao mesmo nível ponto de escolha armazenar substituições e estado da resolvente i. e. qual a cláusula seguinte, para poder regressar 3

Traço com retrocesso avo( abraao, X ) progenitor( abraao, Y ), progenitor( Y, X ) pai( abraao, Y ), progenitor( Y, X ) progenitor( isaac, X ) pai( isaac, X ) Ñ ; progenitor( isaac, X ) mae( isaac, X ) f progenitor( abraao, Y ), progenitor( Y, X ) mae( abraao, Y ), progenitor( Y, X ) f não há mais pontos de escolha ¶ ¶ {Y= isaac } {Y= isaac, X= jacob} ·{Y= isaac } · 4

Ordem das cláusulas determina a ordem por que as soluções são encontradas. • corresponde a trocar a ordem dos ramos na árvore de pesquisa (como o Prolog escolhe sempre o da esquerda. . . ) member( X, [X|Xs] ). member( X, [Z| Xs] ) ¬ member( X, Xs ). member( X, [X|Xs] ). member( X, [1, 2, 3] ) Ñ {X= 1} ; member( X, [1, 2, 3] ) member( X, [2, 3] ) Ñ {X= 2} ; member( X, [2, 3] ) member( X, [3] ) Ñ {X= 3} ; member( X, [3] ) member( X, [] ) f member( X, [1, 2, 3] ) member( X, [3] ) member( X, [] ) f member( X, [3] ) {X= 3} ; member( X, [2, 3] ) {X= 2} ; member( X, [ 1, 2, 3] ) {X= 1} ; no 5

Terminação m computação de um golo — cálculo de todas as soluções m troca de ordem das cláusulas não altera a árvore de pesquisa; só a percorre por ordem diferente se existir um ramo infinito a computação nunca termina não terminação — só com recursão caso perigoso: recursão à esquerda, golo recursivo é o primeiro no corpo programa irmao( X, Y ) ¬ irmao( Y, X ) traço irmao( lot, milcah ) irmao( milcah, lot ) irmao( lot, milcah ) • • • evitar a recursão à esquerda sao_irmaos( X, Y ) ¬ irmao( X, Y ). sao_irmaos( X, Y ) ¬ irmao( Y, X ). a terminação depende também do estado de instanciação dos argumentos — caso do append/3 com o 1º e 3º argumentos listas incompletas, ou member/2, com 2º variável 6

Ordem dos golos determina a árvore de pesquisa. m m m pode a ordem dos resultados ser alterada pode a árvore ser de dimensão muito diferente pode a diferença ser existir ou não um ramo infinito antepassado( A, X ) ¬ antepassado( Y, X) , progenitor( A, Y ). antepassado( A, X ) ¬ progenitor( A, X ). • definição recursiva à esquerda, com ramo infinito — trocar a ordem dos golos avo( A, N ) ¬ progenitor ( Y, N ) , progenitor( A, Y ). neto( A, N ) ¬ progenitor ( A, Y) , progenitor( Y, N ). • padrão de instanciação dos argumentos determina a ordem óptima dos golos • objectivo é falhar depressa! 7

Repetições m em muitas situações, convém evitar repetições nas soluções • minimum( X, Y, X ) ¬ X=< Y. • minimum( X, Y, Y ) ¬ X>= Y. minimum( 2, 2, M ) tem duas soluções iguais, M=2 basta corrigir a lógica para evitar a redundância • minimum( X, Y, Y ) ¬ X> Y. noutros casos, é necessário alterar até a semântica do predicado 8

Equação da PL Algoritmo = Lógica + Controlo m m ideal da PL o Prolog encarregar-se-ia do Controlo deixando aos utilizadores apenas a Lógica das definições axiomáticas estas seriam, por assim dizer, directamente executáveis infelizmente, é necessário conhecer pormenores do modelo de execução do Prolog 9

Aritmética avaliada m Objectivo: ter acesso ao processador aritmético da máquina (eficiência) m soma( X, Y, Z ) ¬ Z is X + Y X, Y têm que estar instanciados a expressão é avaliada e o resultado colocado em Z Perde-se: múltiplos usos do predicado (especializa-se para um uso: soma( X, 2, 5) dá erro) e a estrutura recursiva dos números (não se pode usar unificação mas sim cálculo explícito) % factorial( N, F ) ¬ F é o n-ésimo factorial( N, F ) ¬ N > 0, N 1 is N-1, factorial( N 1, F 1 ), F is N * F 1. factorial( 0, 1 ). 10

Predicados de sistema Aritméticos +, -, *, /, mod Comparação <, =<, >=, =: =, == Avaliação is Z is 2+4 {Z=6} 4 is 2 + X erro, se X não for exp aritmética yes, se X for 2 no, se X for inteiro 2 2+4 = 3+3 no X= 5 -2 {X= 5 -2} unifica 2+4 =: = 3+3 yes avalia 2*3 =< 24/4 yes X = 8 no não unifica 8 mod 3 = 2 yes 8 mod 3 == 2 no X is X + 3 erro, se X não for exp aritmética no, cc 7 is 28/4 yes 11

Iteração m implementação da recursão: cada chamada implica guardar uma estrutura na stack com as variáveis temporárias que podem vir a ser precisas m espaço ocupado linear no número de chamadas recursivas não há construções iterativas, mas há implementações iterativas de programas recursivos quando o golo recursivo é o último do corpo da cláusula, não há mais pontos de escolha e portanto o espaço ocupado pela chamada anterior pode ser reaproveitado 12

Programa iterativo ao chamar, N e T já não são mais precisos e F é sempre o mesmo, pois só na última chamada recebe o valor no acumulador trata-se de recursão à direita ou recursão na cauda comparar com factorial/2 atrás, que não tem recursão à direita % factorial ¬ F é o factorial de N factorial( N, F ) ¬ factorial( N, 1, F ). factorial( N, T, F ) ¬ N > 0, T 1 is T*N, N 1 is N-1, factorial( N 1, T 1, F ). factorial( 0, F, F ). 13

Pontos de escolha m na variante 1 não se criam pontos de escolha m variante 2: cria ponto de escolha m a unificação do golo com a outra cabeça é impossível, pelo que não há cláusulas alternativas utilizáveis a criação de um ponto de escolha é pesada: armazenar o ponto da execução, mais o estado de instanciação das variáveis está-se a atrasar a unificação para dentro do corpo da cláusula, em vez de resolver logo com a unificação na cabeça Variante 1 lista([]). lista([X|Xs]) : - lista( Xs ). Chamada: lista( [1, 2, 3]) m Variante 2 lista(Xs) : - Xs = []. lista(X) : - X=[X|Xs], lista( Xs ). Chamada: lista( [1, 2, 3]) 14

Meta-variável m em Prolog, tanto os dados como os programas são representados como termos lógicos é possível manipular os programas como se fossem dados e vice -versa através do meta-predicado call(X) • meta-predicado, porque a sua execução é chamar o seu argumento como se fosse um golo [read( G ), call( G ) — lê um termo da entrada e executa-o] meta-variável — simplificação sintáctica: em vez de call( X ) usar simplesmente X [read( G ), G ] • definição da disjunção: % X ; Y ¬ X ou Y X ; Y ¬ X. X ; Y ¬ Y. • se, no momento da chamada, a meta-variável estiver por instanciar, dá erro 15

Programa errado % fib( N, F ) ¬ F é o número de Fibonnacci de ordem N fib( 1, 1 ). fib( 2, 1 ). fib( N, F ) ¬ N 1 is N-1, N 2 is N-2, fib( N 1, F 1 ), fib( N 2, F 2 ), F is F 1+F 2. • série: 1 1 2 3 5 8 13 21 34. . . 16

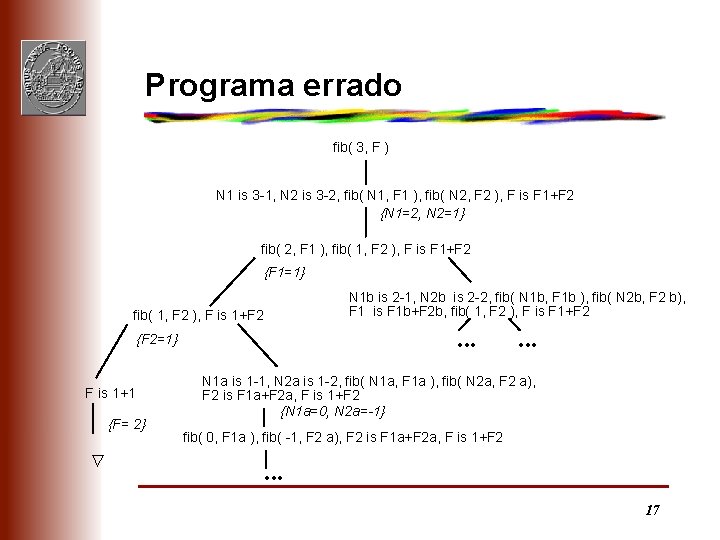
Programa errado fib( 3, F ) N 1 is 3 -1, N 2 is 3 -2, fib( N 1, F 1 ), fib( N 2, F 2 ), F is F 1+F 2 {N 1=2, N 2=1} fib( 2, F 1 ), fib( 1, F 2 ), F is F 1+F 2 {F 1=1} N 1 b is 2 -1, N 2 b is 2 -2, fib( N 1 b, F 1 b ), fib( N 2 b, F 2 b), F 1 is F 1 b+F 2 b, fib( 1, F 2 ), F is F 1+F 2 fib( 1, F 2 ), F is 1+F 2 {F 2=1} F is 1+1 {F= 2} Ñ • • • N 1 a is 1 -1, N 2 a is 1 -2, fib( N 1 a, F 1 a ), fib( N 2 a, F 2 a), F 2 is F 1 a+F 2 a, F is 1+F 2 {N 1 a=0, N 2 a=-1} fib( 0, F 1 a ), fib( -1, F 2 a), F 2 is F 1 a+F 2 a, F is 1+F 2 • • • 17

Solução com guarda % fib( N, F ) ¬ F é o número de Fibonnacci de ordem N guarda • • fib( 1, 1 ). fib( 2, 1 ). fib( N, F ) ¬ N>2, N 1 is N-1, N 2 is N-2, fib( N 1, F 1 ), fib( N 2, F 2 ), F is F 1+F 2. a guarda funciona como uma espécie de extensão da unificação na cabeça a provocar um retrocesso superficial (logo no 1º golo) assim o programa computa só as soluções pretendidas 18

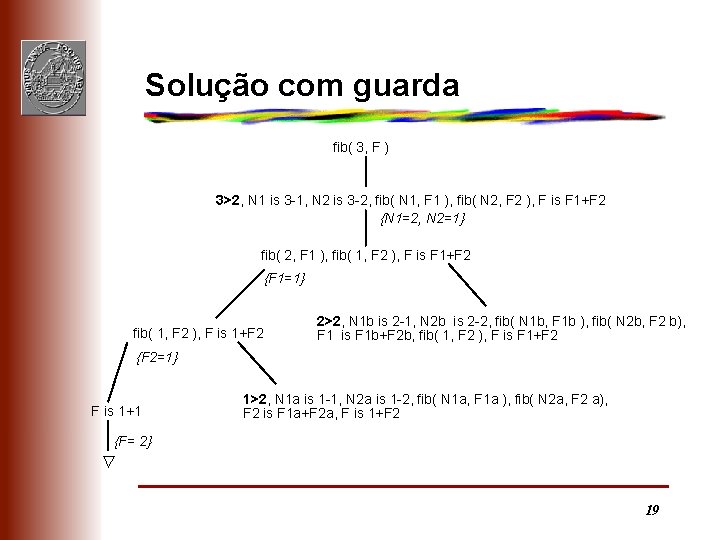
Solução com guarda fib( 3, F ) 3>2, N 1 is 3 -1, N 2 is 3 -2, fib( N 1, F 1 ), fib( N 2, F 2 ), F is F 1+F 2 {N 1=2, N 2=1} fib( 2, F 1 ), fib( 1, F 2 ), F is F 1+F 2 {F 1=1} fib( 1, F 2 ), F is 1+F 2 2>2, N 1 b is 2 -1, N 2 b is 2 -2, fib( N 1 b, F 1 b ), fib( N 2 b, F 2 b), F 1 is F 1 b+F 2 b, fib( 1, F 2 ), F is F 1+F 2 {F 2=1} F is 1+1 1>2, N 1 a is 1 -1, N 2 a is 1 -2, fib( N 1 a, F 1 a ), fib( N 2 a, F 2 a), F 2 is F 1 a+F 2 a, F is 1+F 2 {F= 2} Ñ 19

Solução com cut % fib( N, F ) ¬ F é o número de Fibonnacci de ordem N fib( 1, 1 ) ¬ !. fib( 2, 1 ) ¬ !. fib( N, F ) ¬ N 1 is N-1, N 2 is N-2, fib( N 1, F 1 ), fib( N 2, F 2 ), F is F 1+F 2. • fib/2 fica determinista 20

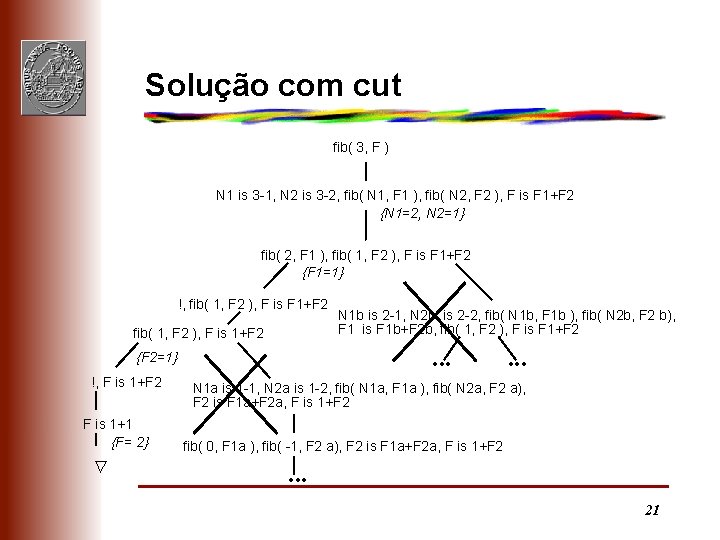
Solução com cut fib( 3, F ) N 1 is 3 -1, N 2 is 3 -2, fib( N 1, F 1 ), fib( N 2, F 2 ), F is F 1+F 2 {N 1=2, N 2=1} fib( 2, F 1 ), fib( 1, F 2 ), F is F 1+F 2 {F 1=1} !, fib( 1, F 2 ), F is F 1+F 2 fib( 1, F 2 ), F is 1+F 2 {F 2=1} !, F is 1+F 2 F is 1+1 {F= 2} Ñ N 1 b is 2 -1, N 2 b is 2 -2, fib( N 1 b, F 1 b ), fib( N 2 b, F 2 b), F 1 is F 1 b+F 2 b, fib( 1, F 2 ), F is F 1+F 2 • • • N 1 a is 1 -1, N 2 a is 1 -2, fib( N 1 a, F 1 a ), fib( N 2 a, F 2 a), F 2 is F 1 a+F 2 a, F is 1+F 2 fib( 0, F 1 a ), fib( -1, F 2 a), F 2 is F 1 a+F 2 a, F is 1+F 2 • • • 21

Cut o cut (!) é um predicado de sistema que expressa determinismo • se um golo unificou com a cabeça fib( 1, 1 ), não há hipótese de encontrar outra solução, usando outra cláusula Tratamento do cut — o golo cut sucede e comete o Prolog com todas as escolhas feitas desde que o golo pai unificou com a cláusula onde o cut ocorre. o cut corta todas as cláusulas abaixo dele (na definição do mesmo predicado) o cut corta todas as soluções alternativas dos golos que lhe ficam à esquerda na cláusula o cut não corta os golos que lhe ficam à direita na cláusula • estes podem produzir várias soluções em retrocesso • retrocesso no cut falha e provoca a escolha da última alternativa antes da escolha da cláusula que contém o cut 22

Cut verde m cut verde — cut que, se retirado, não afecta as soluções produzidas m só serve para evitar ao Prolog o trabalho de percorrer ramos falhados da árvore de pesquisa [seria o caso de fib/3 com cuts e com a guarda N>2] problema: a formulação do efeito do cut é muito operacional e destrói, em muitos casos, a declaratividade das definições de predicados só simulando a execução se percebe o comportamento do programa 23

Predicado determinista m exemplo de cuts verdes — predicado determinista, isto é, em cada caso só uma cláusula é aplicável optimização da recursão na cauda, garantida pondo um cut antes do último golo, porque deixa de haver pontos de escolha para a computação do golo dessa cláusula % fusao( Xs, Ys, Zs ) ¬ Zs é a lista ordenada com a fusão das listas ordenadas Xs e Ys fusao( [X|Xs], [Y|Ys], [X|Zs] ) ¬ X<Y, !, fusao( Xs, [Y|Ys], Zs ). fusao( [X|Xs], [Y|Ys], [X, Y|Zs] ) ¬ X=Y, !, fusao( Xs, Ys, Zs ). fusao( [X|Xs], [Y|Ys], [Y|Zs] ) ¬ X>Y, !, fusao( [X|Xs], Ys, Zs ). fusao( Xs, [], Xs ) ¬ !. fusao( [], Ys ) ¬ !. 24

Cut vermelho m cut vermelho — cut que, se retirado, altera as soluções produzidas usa-se para implementar (parcialmente) a negação por falha; para eliminar soluções indesejadas [a segunda cláusula de ordena/2 só se atinge se não se passar pelo cut na primeira]: é perigoso! Basta alterar a ordem das cláusulas para ter resultados errados; evitar o cálculo de ordenada/1, a negação da condição de cima % ordena( Xs, Ys ) ¬ Ys é a lista ordenada dos elementos de Xs ordena( Xs, Ys ) ¬ append( As, [X, Y|Bs], Xs ), X>Y, !, append( As, [Y, X|Bs], Xs 1 ), ordena( Xs 1, Ys ). ordena( Xs, Xs ). % ¬ ordenada( Xs ), !. 25

Implementação da negação % nao( X ) ¬ não se consegue provar X nao( X ) ¬ X, !, fail. nao( X ). m m m este cut é vermelho (se o retirar, nao(X) sucede sempre) trocar a ordem das cláusulas não se limita a trocar a ordem das soluções — passa a dar soluções erradas a negação dá resultados inesperados se o golo for chamado com argumentos não fechados 26

Uso do cut % estudante_solteiro( X ) ¬ X é estudante e X não é casado estudante_solteiro( X ) ¬ nao( casado(X) ), estudante( X ). estudante( quim ). casado( ze ). golo estudante_solteiro( X ) falha porque casado( X ) sucede com X=ze, embora X=quim seja uma solução; trocando a ordem já sucede porque chama nao( casado( quim ) ) fechado 27

Se-então-senão % P -> Q ; R ¬ se P então Q, senão R P -> Q ; R ¬ P, !, Q. P -> Q ; R ¬ R. este cut é vermelho, porque se baseia na supressão da condição da 2ª cláusula • P -> Q ; R ¬ not P, R. • a vantagem é precisamente evitar a duplicação da avaliação de P % minimo( X, Y, Z ) ¬ Z é o mínimo entre X e Y minimo( X, Y, Z ) ¬ (X=<Y -> Z=X ; Z=Y). % minimo( X, Y, Z ) ¬ Z é o mínimo entre X e Y minimo( X, Y, X ) ¬ X=<Y, !. minimo( X, Y, Y ). 28