Projection Pursuit Projection Pursuit PP PCA and FDA



















- Slides: 22

Projection Pursuit

Projection Pursuit (PP) PCA and FDA are linear, PP may be linear or non-linear. Find interesting “criterion of fit”, or “figure of General transformation with merit” function, parameters W. that allows for low-dim (usually 2 D or 3 D) Index of “interestingness” projection. Interesting indices may use a priori knowledge about the problem: 1. mean nearest neighbor distance – increase clustering of Y(j) 2. maximize mutual information between classes and features

Kurtosis ICA is a special version of PP, recently very popular. Gaussian distributions of variable Y are characterized by 2 parameters: mean measure value: of non-Gaussianity of One simple projections is the variance: 4 -th moment of the of distribution, called These are the(cumulant) first 2 moments distribution; all kurtosis, measures “skewedness” of the higher are 0 for G(Y). Super-Gaussian distribution: longis: distribution. For E{Y} =0 kurtosis tail, peak at zero, k 4(y)>0, like binary image data. sub-Gaussian distribution is more flat

Correlation and independence Variables are statistically independent if their joint probability distribution is a product of probabilities for all variables: Features Yi, Yj are uncorrelated if covariance is diagonal, or: Uncorrelated features are orthogonal. Statistically independent features Yi, Yj for any functions give: This is much stronger condition than correlation; in particular the functions may be powers of variables; any non-Gaussian distribution after

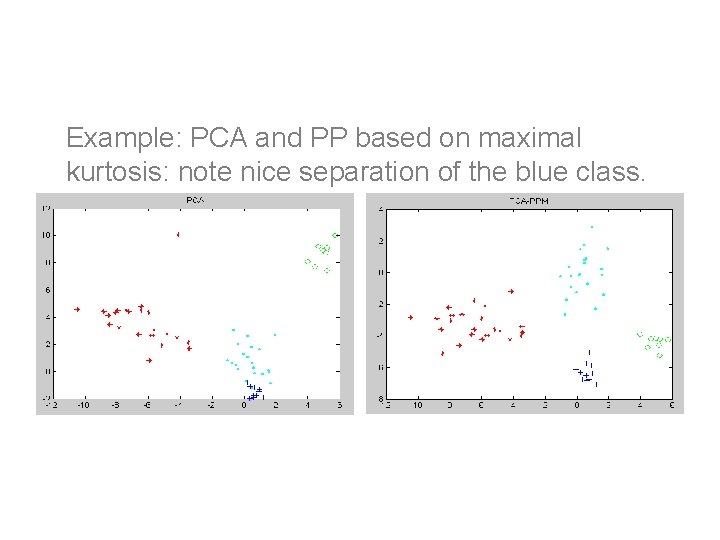
PP/ICA example Example: PCA and PP based on maximal kurtosis: note nice separation of the blue class.

Some remarks • Many formulations of PP and ICA methods exist. • PP is used for data visualization and dimensionality reduction. • Nonlinear projections are frequently Index I(Y; W) is considered, but solutions arebased more here numerically on intensive. maximum variance. Other components are found in the space T X viewed as PP, max (for • orthogonal PCA mayto also W 1 be standardized data): Same index is used, with projection on space orthogonal to k-1 PCs.

How do we find multiple Projections • Statistical approach is complicated: – Perform a transformation on the data to eliminate structure in the already found direction – Then perform PP again • Neural Comp approach: Lateral

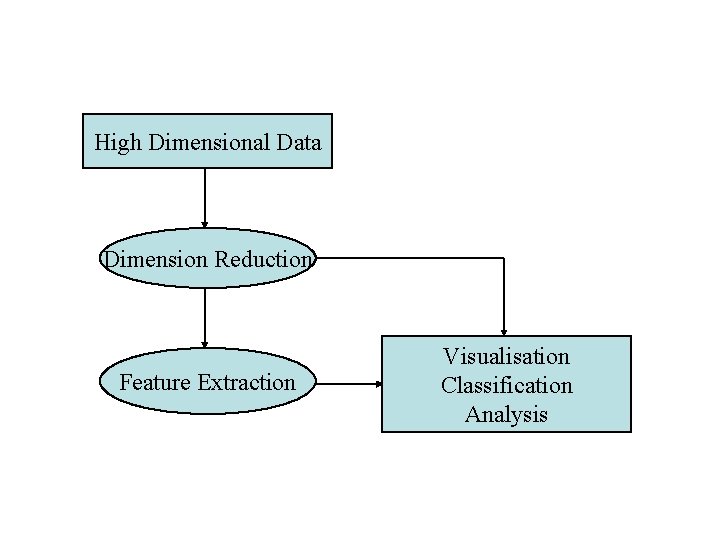
High Dimensional Data Dimension Reduction Feature Extraction Visualisation Classification Analysis


Projection Pursuit what: An automated procedure that seeks interesting low dimensional projections of a high dimensional cloud by numerically maximizing an objective function or projection index. Huber, 1985

Projection Pursuit • • • why: Curse of dimensionality Less Robustness worse mean squared error greater computational cost slower convergence to limiting distributions … • Required number of labelled samples increases with dimensionality.

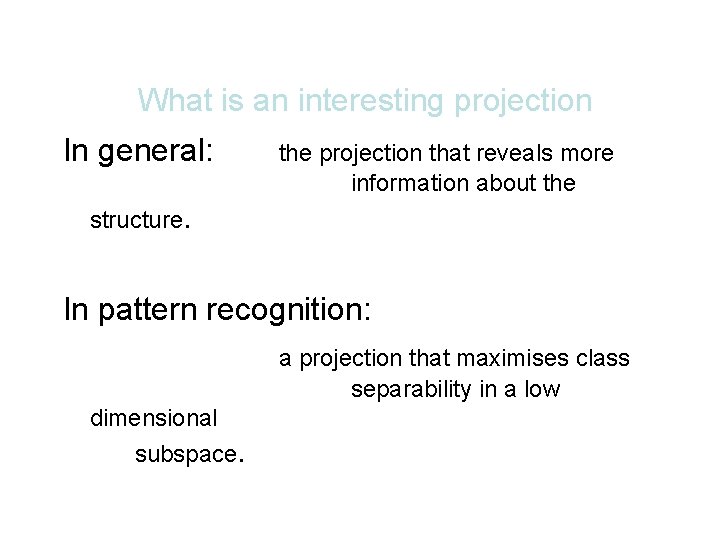
What is an interesting projection In general: the projection that reveals more information about the structure. In pattern recognition: a projection that maximises class separability in a low dimensional subspace.

Projection Pursuit Dimensional Reduction Find lower-dimensional projections of a high-dimensional point cloud to facilitate classification. Exploratory Projection Pursuit Reduce the dimension of the problem to facilitate visualization.

Projection Pursuit How many dimensions to use • for visualization • for classification/analysis Which Projection Index to use • measure of variation (Principal Components) • departure from normality (negative entropy) • class separability(distance, Bhattacharyya, Mahalanobis, . . . ) • …

Projection Pursuit Which optimization method to choose We are trying to find the global optimum among local ones • hill climbing methods (simulated annealing) • regular optimization routines with random starting points.

Timetable for Dimensionality reduction • Begin 16 April 1998 • Report on the state-of-the-art. 1 June 1998 • Begin software implementation 15 June 1998 • Prototype software presentation 1 November 1998

ICA demos • ICA has many applications in signal and image analysis. • Finding independent signal sources allows for separation of signals from different sources, removal of noise or artifacts. Both W and Y are unknown! This is a blind Observations X are a linear mixture W of separation problem. unknown sources Y How can they be found? If Y are Independent Components and W linear Play with ICALab PCA/ICA Matlab software for mixing the problem is similar to FDA or PCA, signal/image analysis: only the criterion function is different. http: //www. bsp. brain. riken. go. jp/page 7. ht

ICA demo: images & audio Example from Cichocki’s lab, http: //www. bsp. brain. riken. go. jp/page 7. html X space for images: take intensity of all pixels one vector per image, or take smaller patches (ex: 64 x 64), increasing # vectors • 5 images: originals, mixed, convergence of ICA iterations

Self-organization PCA, FDA, ICA, PP are all inspired by statistics, although some neural-inspired methods have been proposed to find interesting solutions, especially for their non-linear versions. • Brains learn to discover the structure of signals: visual, tactile, olfactory, auditory (speech and sounds). • This is a good example of unsupervised learning: spontaneous development of feature detectors, compressing internal information that is needed

Models of self-organizaiton SOM or SOFM (Self-Organized Feature Mapping) – self-organizing feature map, one of the models. Howsimplest can such maps develop spontaneously? Local neural connections: neurons interact strongly with those nearby, but weakly with those that are far (in addition inhibiting some History: intermediate neurons). von der Malsburg and Willshaw (1976), competitive learning, Hebb mechanisms, „Mexican hat” interactions, models of visual systems. Amari (1980) – models of continuous neural tissue.

Computational Intelligence: Methods and Applications Lecture 8 Projection Pursuit & Independent Component Analysis Włodzisław Duch SCE, NTU, Singapore 21

Computational Intelligence: Methods and Applications Lecture 6 Principal Component Analysis. Włodzisław Duch SCE, NTU, Singapore http: //www. ntu. edu. sg/home/aswduch 22