Projection Projection Projection Conceptual model of 3 D

Projection

Projection

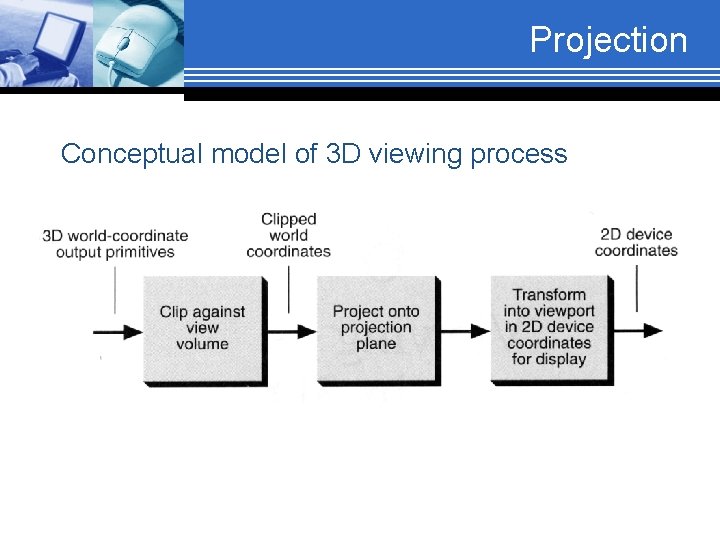
Projection Conceptual model of 3 D viewing process

Projection § In general, projections transform points in a coordinate system of dimension n into points in a coordinate system of dimension less than n. § We shall limit ourselves to the projection from 3 D to 2 D. § We will deal with planar geometric projections where: ³ The projection is onto a plane rather than a curved surface ³ The projectors are straight lines rather than curves

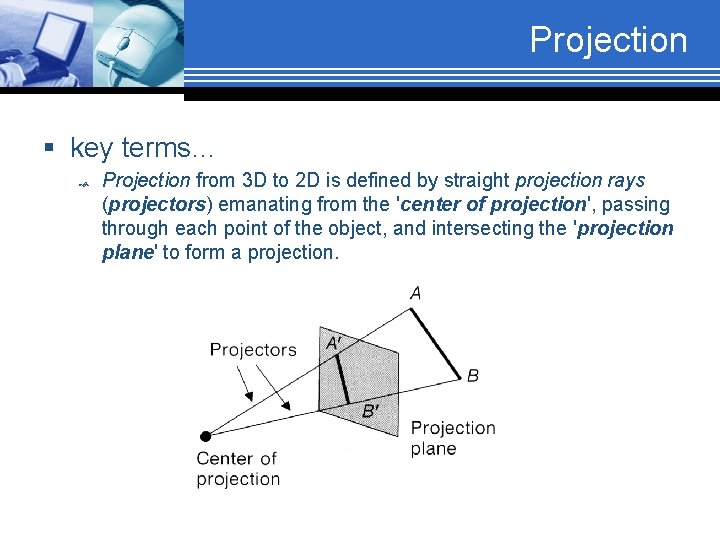
Projection § key terms… Projection from 3 D to 2 D is defined by straight projection rays (projectors) emanating from the 'center of projection', passing through each point of the object, and intersecting the 'projection plane' to form a projection.

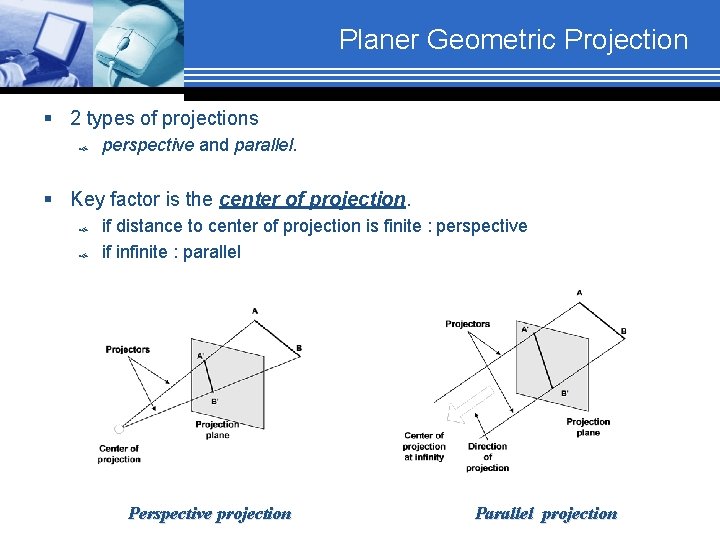
Planer Geometric Projection § 2 types of projections perspective and parallel. § Key factor is the center of projection. if distance to center of projection is finite : perspective if infinite : parallel Perspective projection Parallel projection

Perspective v Parallel § Perspective: visual effect is similar to human visual system. . . has 'perspective foreshortening' § size of object varies inversely with distance from the center of projection. Parallel lines do not in general project to parallel lines angles only remain intact for faces parallel to projection plane.

Perspective v Parallel § Parallel: less realistic view because of no foreshortening however, parallel lines remain parallel. angles only remain intact for faces parallel to projection plane.

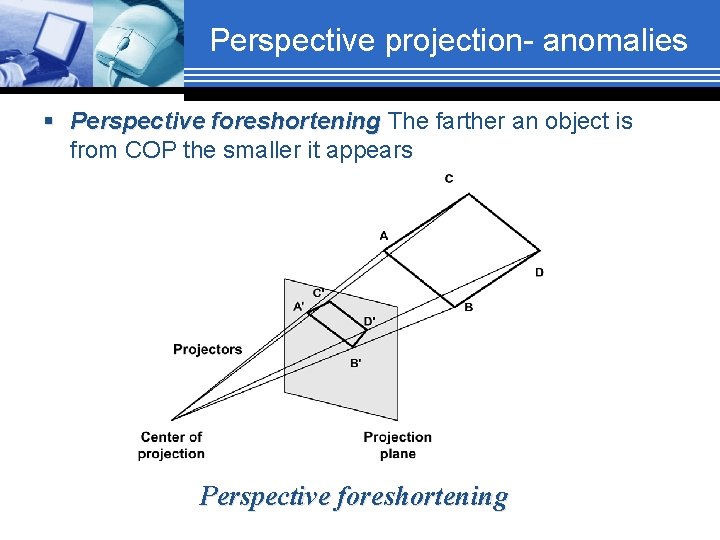
Perspective projection- anomalies § Perspective foreshortening The farther an object is from COP the smaller it appears Perspective foreshortening

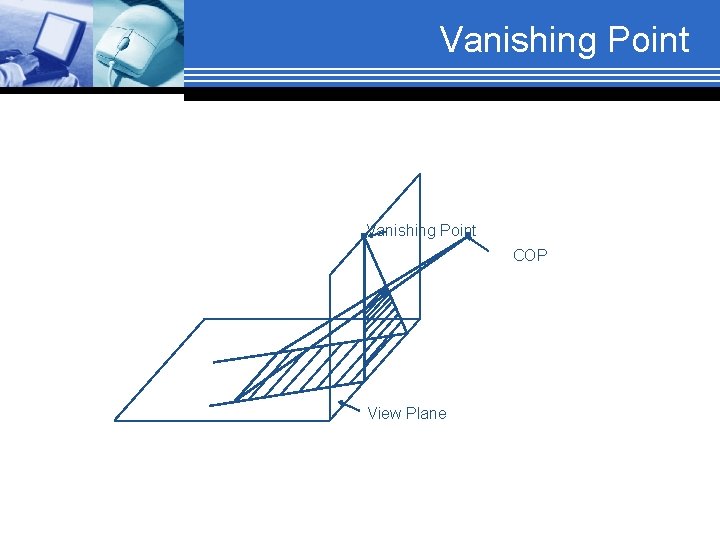
Perspective projection- anomalies § Vanishing Points: Any set of parallel lines not parallel to the view plane appear to meet at some point. There an infinite number of these, 1 for each of the infinite amount of directions line can be oriented Vanishing point

Perspective projection- anomalies § View Confusion: Objects behind the center of projection are projected upside down and backward onto the view-plane § Topological distortion: A line segment joining a point which lies in front of the viewer to a point in back of the viewer is projected to a broken line of infinite extent. P'3 P 1 Y Plane containing Center of Projection (C) P 3 C View Plane P 2 P'1 X Z

Vanishing Point COP View Plane

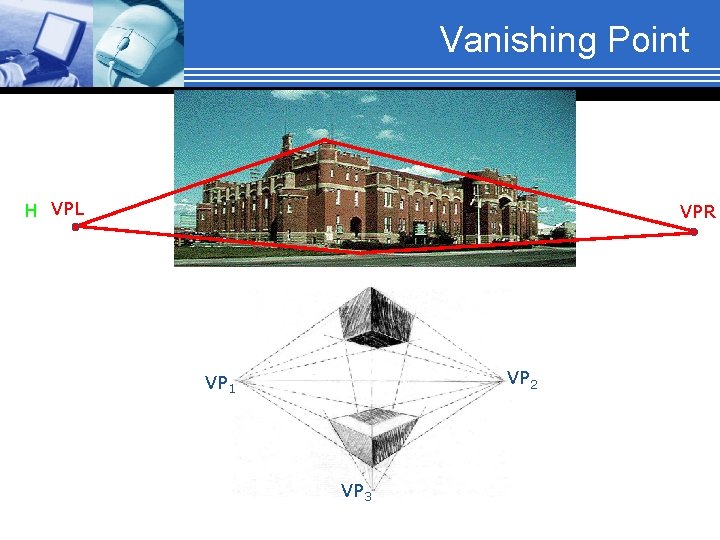
Vanishing Point § If a set of lines are parallel to one of the three axes, the vanishing point is called an axis vanishing point (Principal Vanishing Point). § § § There at most 3 such points, corresponding to the number of axes cut by the projection plane One-point: One principle axis cut by projection plane One axis vanishing point Two-point: Two principle axes cut by projection plane Two axis vanishing points Three-point: Three principle axes cut by projection plane Three axis vanishing points

Vanishing Point

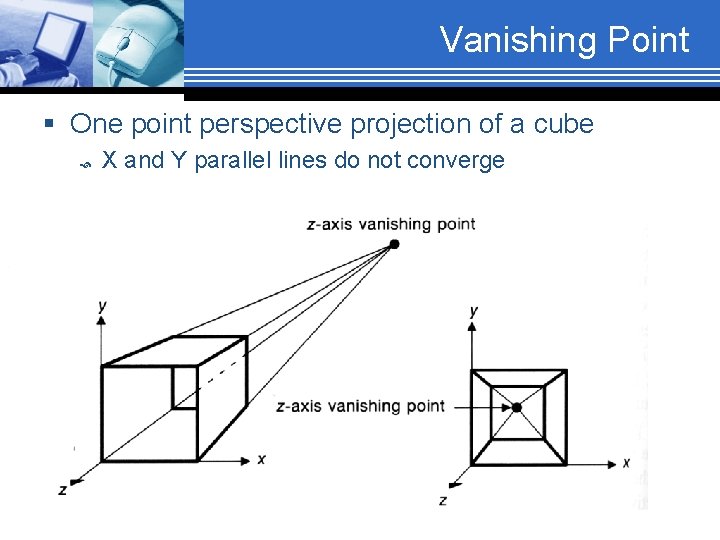
Vanishing Point § One point perspective projection of a cube X and Y parallel lines do not converge

Vanishing Point

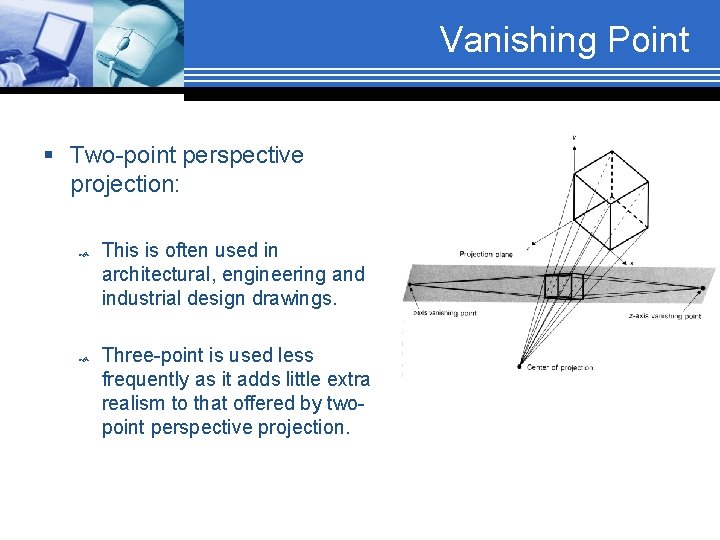
Vanishing Point § Two-point perspective projection: This is often used in architectural, engineering and industrial design drawings. Three-point is used less frequently as it adds little extra realism to that offered by twopoint perspective projection.

Vanishing Point H VPL VPR VP 2 VP 1 VP 3

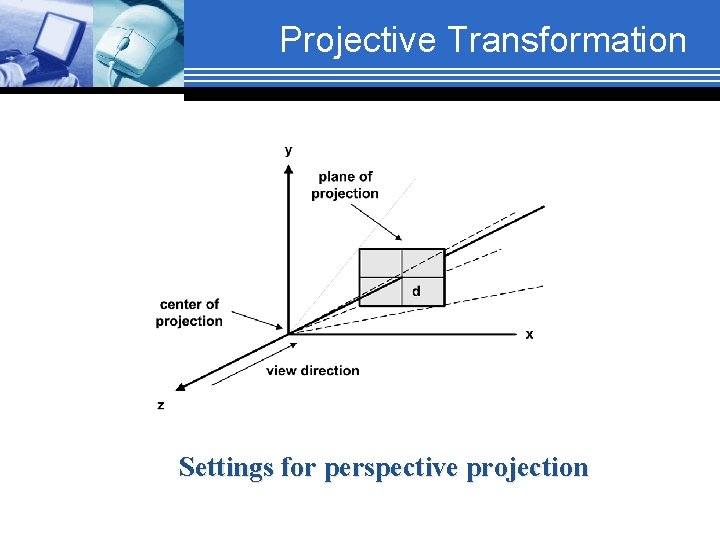
Projective Transformation Settings for perspective projection

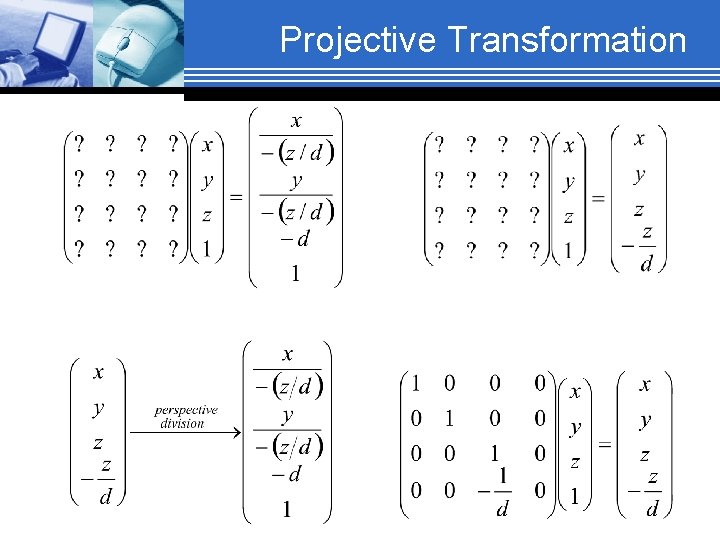
Projective Transformation

Projective Transformation

Parallel projection § 2 principle types: orthographic and oblique. § Orthographic : direction of projection = normal to the projection plane. § Oblique : direction of projection != normal to the projection plane.

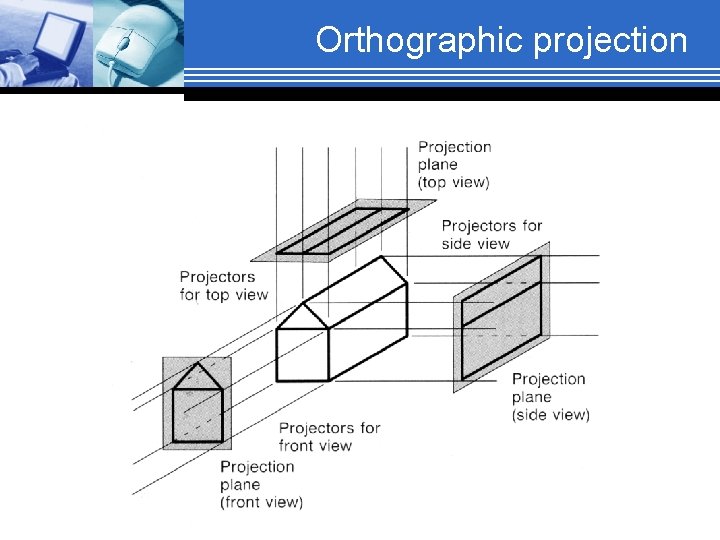
Orthographic projection § Orthographic (or orthogonal) projections: front elevation, top-elevation and side-elevation. all have projection plane perpendicular to a principle axes. § Useful because angle and distance measurements can be made. . . § However, As only one face of an object is shown, it can be hard to create a mental image of the object, even when several view are available

Orthographic projection

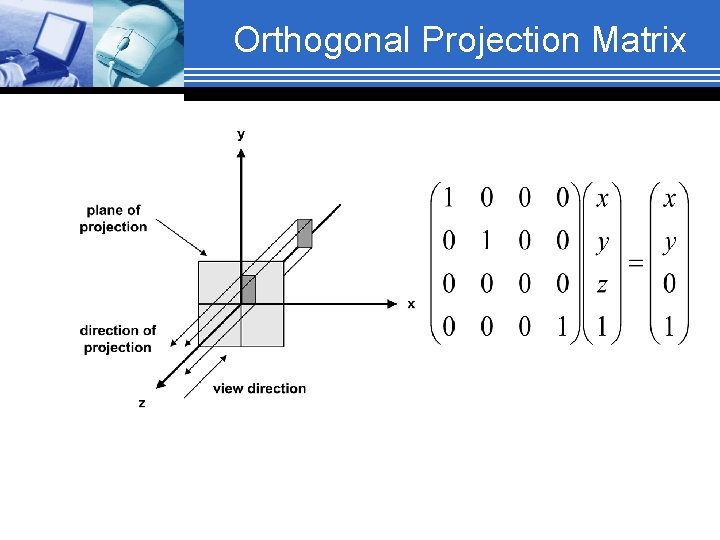
Orthogonal Projection Matrix

Axonometric projection § Axonometric Projections use projection planes that are not normal to a principal axis. On the basis of projection plane normal N = (dx, dy, dz) dz subclasses are: o Isometric : | dx | = | dy | = | dz | i. e. N makes equal angles with all principal axes. o Dimetric : | dx | = | dy | o Trimetric : | dx | != | dy | != | dz |

Axonometric vs Perspective § Axonometric projection shows several faces of an object at once like perspective projection. § But the foreshortening is uniform rather than being related to the distance from the COP. Isometric proj Projection Plane

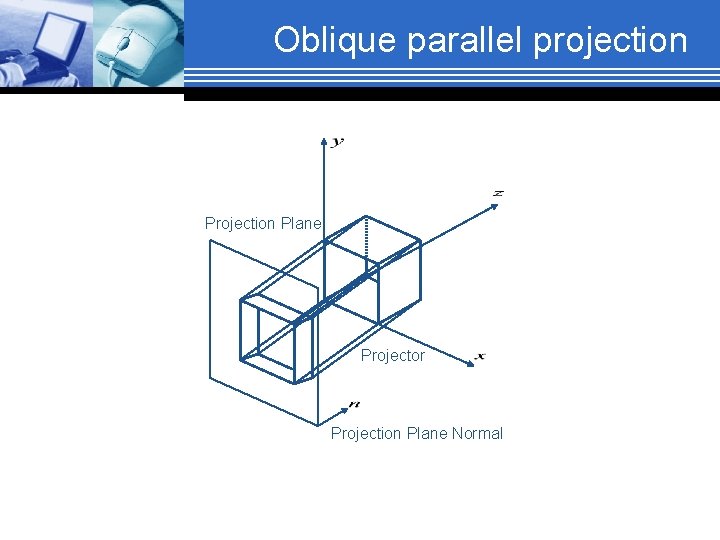
Oblique parallel projection § Oblique parallel projections Objects can be visualized better then with orthographic projections Can measure distances, but not angles * Can only measure angles for faces of objects parallel to the plane § 2 common oblique parallel projections: Cavalier and Cabinet

Oblique parallel projection Plane Projector Projection Plane Normal

Oblique parallel projection § Cavalier: The direction of the projection makes a 45 degree angle with the projection plane. There is no foreshortening

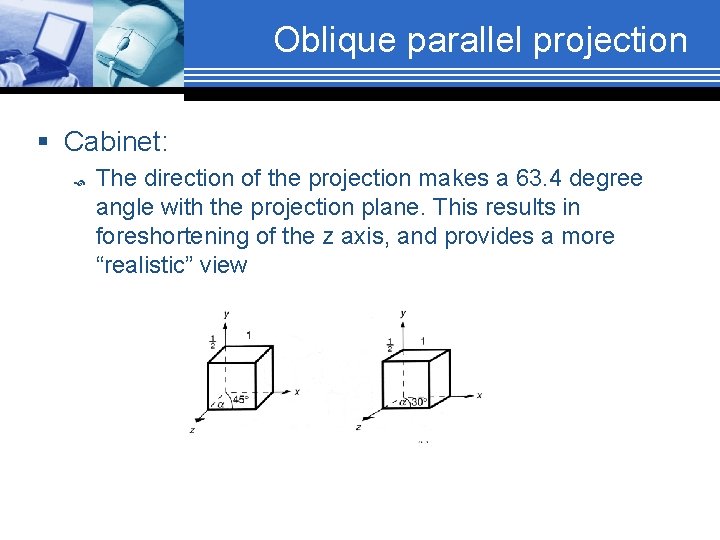
Oblique parallel projection § Cabinet: The direction of the projection makes a 63. 4 degree angle with the projection plane. This results in foreshortening of the z axis, and provides a more “realistic” view

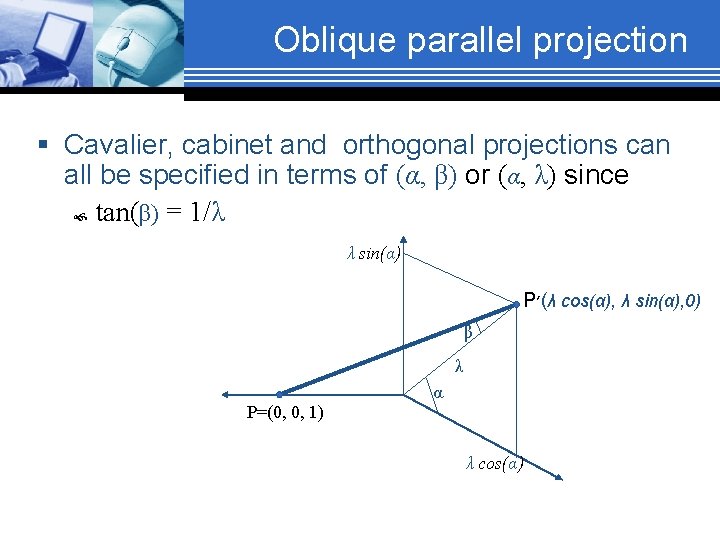
Oblique parallel projection § Cavalier, cabinet and orthogonal projections can all be specified in terms of (α, β) or (α, λ) since tan(β) = 1/λ λ sin(α) P (׳ λ cos(α), λ sin(α), 0) β λ P=(0, 0, 1) α λ cos(α)

Oblique parallel projection l=1 b = 45 Cavalier projection a = 0 - 360 l=0. 5 b = 63. 4 Cabinet projection a = 0 – 360 l=0 b = 90 a = 0 – 360 Orthogonal projection

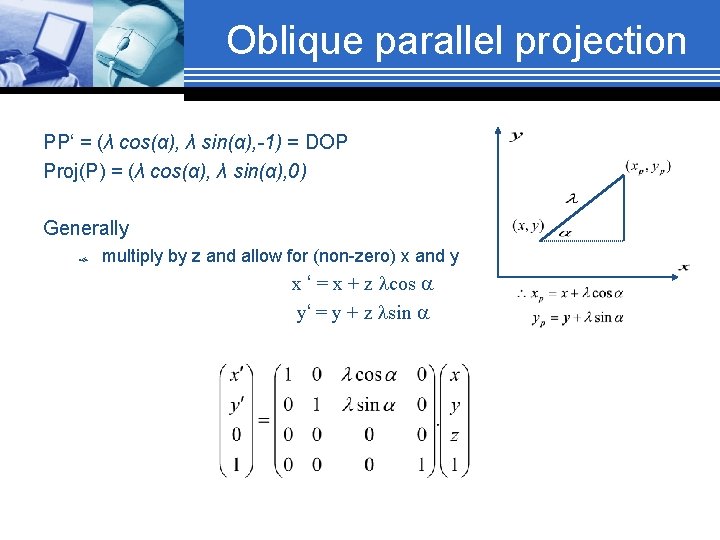
Oblique parallel projection PP‘ = (λ cos(α), λ sin(α), -1) = DOP Proj(P) = (λ cos(α), λ sin(α), 0) Generally multiply by z and allow for (non-zero) x and y x ‘ = x + z lcos a y‘ = y + z lsin a

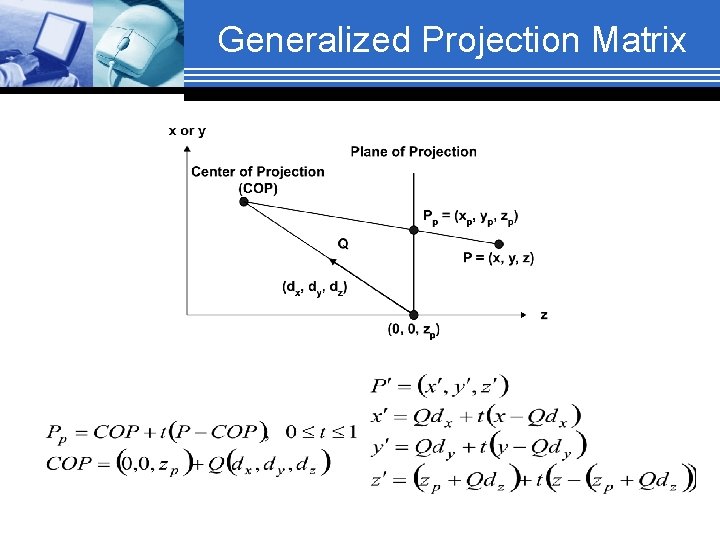
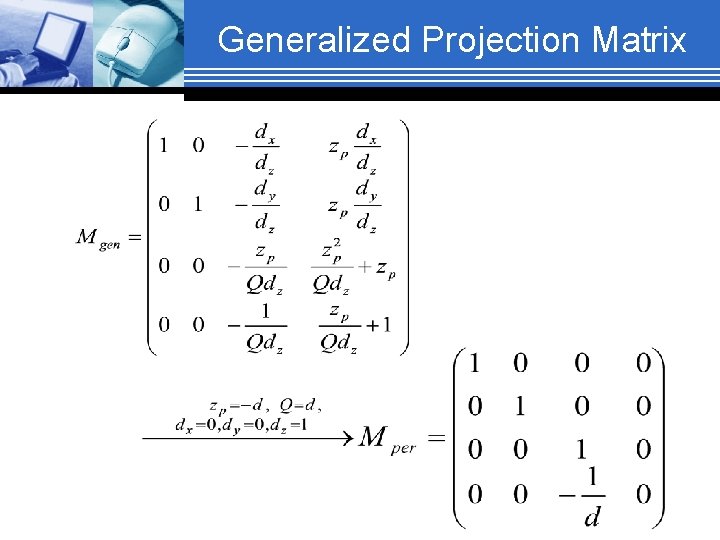
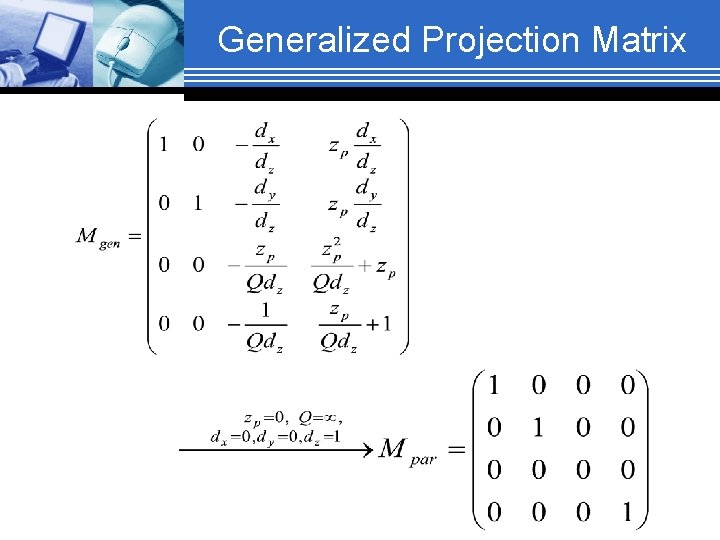
Generalized Projection Matrix

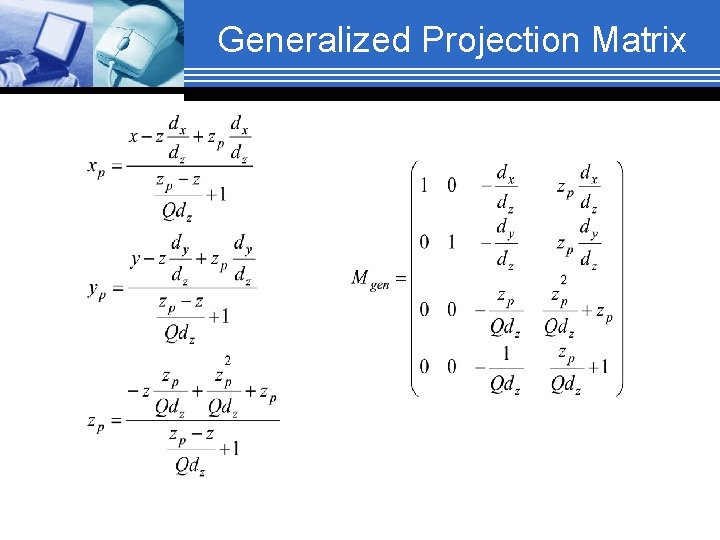
Generalized Projection Matrix

Generalized Projection Matrix

Generalized Projection Matrix

Generalized Projection Matrix

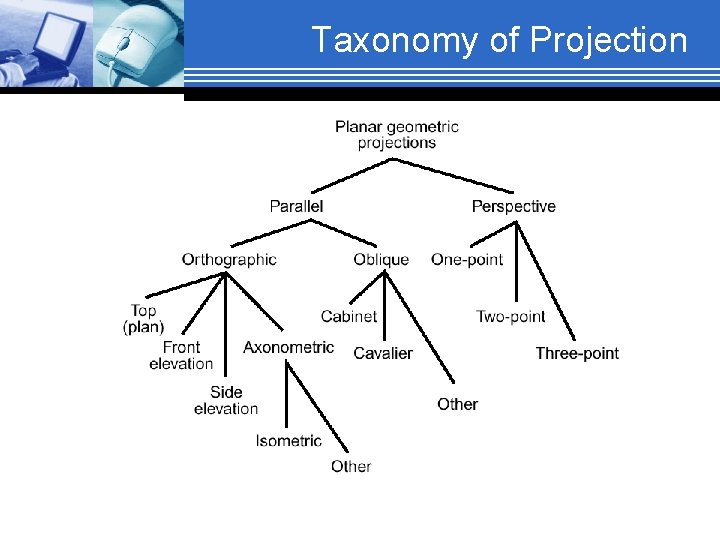
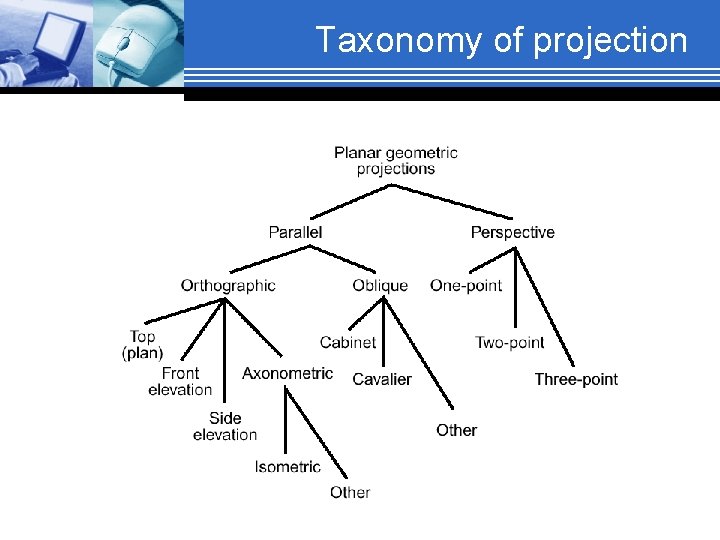
Taxonomy of Projection

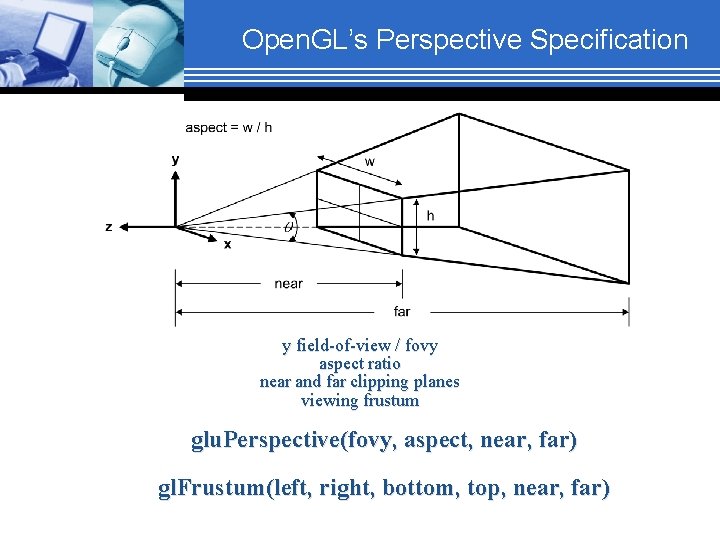
Open. GL’s Perspective Specification y field-of-view / fovy aspect ratio near and far clipping planes viewing frustum glu. Perspective(fovy, aspect, near, far) gl. Frustum(left, right, bottom, top, near, far)

Perspective without Depth • The depth information is lost as the last two components are same • But dept information of the projected points is essential for hidden surface removal and other purposes like blending, shading etc.

Perspective without Depth For ß < 0, z’ is a monotonically increasing function of depth.

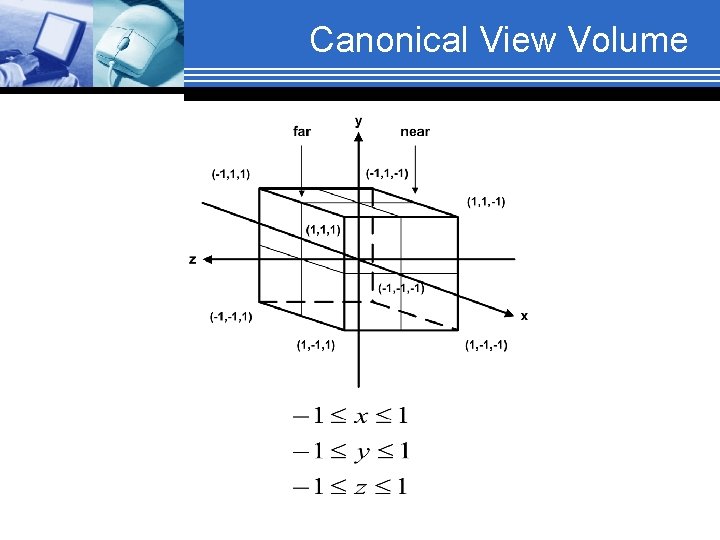
Canonical View Volume

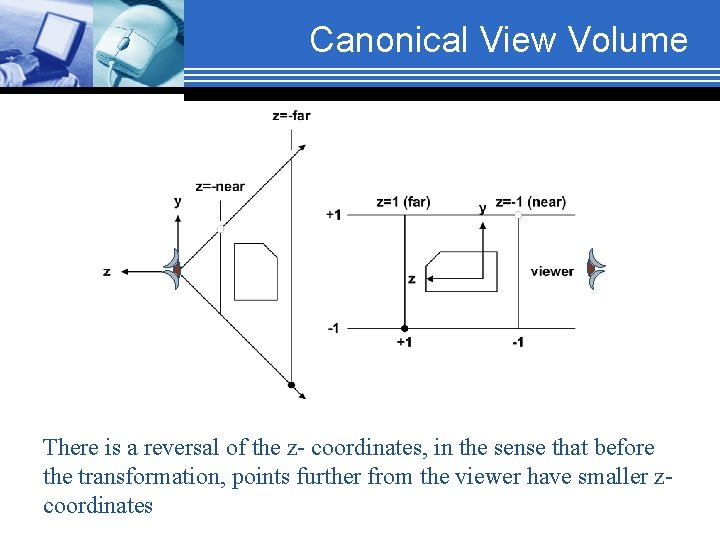
Canonical View Volume There is a reversal of the z- coordinates, in the sense that before the transformation, points further from the viewer have smaller zcoordinates

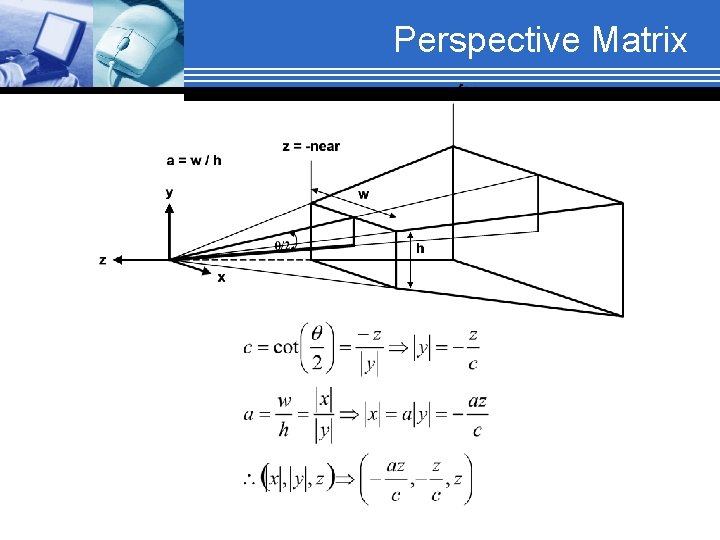
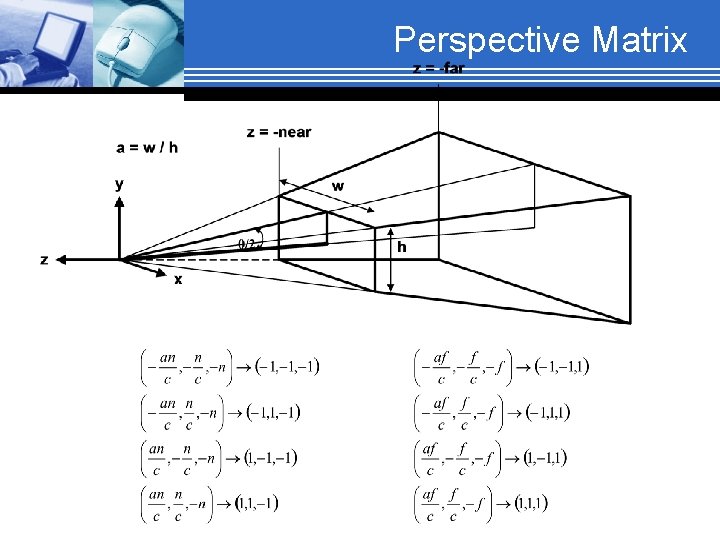
Perspective Matrix The matrix to perform perspective transformation: transformation

Perspective Matrix

Perspective Matrix

Perspective Matrix

Perspective Matrix

Perspective Matrix The matrix to perform perspective transformation: transformation

Taxonomy of projection

Generalized Projection § Using the origin as the center of projection, derive the perspective transformation onto the plane passing through the point R 0(x 0, y 0, z 0) and having the normal vector N = n 1 I + n 2 J + n 3 K y R 0=x 0 , y 0, z 0 P'(x', y', z') O z x P(x, y, z)

Generalized Projection N = n 1 I + n 2 J + n 3 K P'O = α PO x' = αx, y' = αy, z ' = αz y R 0=x 0 , y 0, z 0 N. R 0 P' = 0 n 1 x ' + n 2 y ' + n 3 z ' =n 1 x 0 + n 2 y 0 + n 3 z 0 = d 0 P'(x', y', z') O z x P(x, y, z)

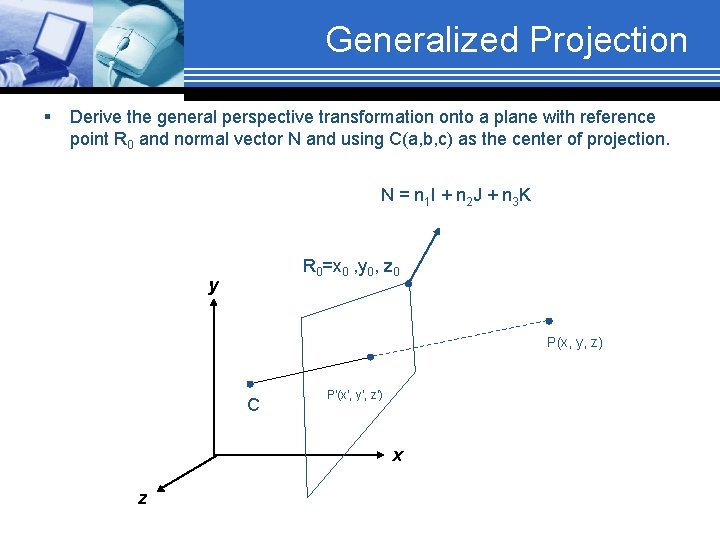
Generalized Projection § Derive the general perspective transformation onto a plane with reference point R 0 and normal vector N and using C(a, b, c) as the center of projection. N = n 1 I + n 2 J + n 3 K R 0=x 0 , y 0, z 0 y P(x, y, z) C P'(x', y', z') x z

Generalized Projection P'C = α PC x' = α(x-a) + a N = n 1 I + n 2 J + n 3 K n 1 x' + n 2 y' + n 3 z‘ = d 0 R 0=x 0 , y 0, z 0 y P(x, y, z d = (n 1 x 0 + n 2 y 0 + n 3 z 0) – (n 1 a + n 2 b + n 3 c) = d 0 – d 1 C P'(x', y', z') x z

Generalized Projection § Follow the steps – Translate so that C lies at the origin Per Translate back

Generalized Projection § Find (a) the vanishing points for a given perspective transformation in the direction given by a vector U (b) principal vanishing point. § Family of parallel lines having the direction U(u 1, u 2, u 3) can be written in parametric form as x = u 1 t+p, y = u 2 t+q, z = u 3 t+r here (p, q, r) is any point on the line § Let, proj(x, y, z, 1) = (x‘, y‘, z‘, h) x' = (d+an 1)(u 1 t+p) + an 2(u 2 t+q) + an 3(u 3 t+r) – ad 0 y' = bn 1(u 1 t+p) + (d+bn 2)(u 2 t+q) + bn 3(u 3 t+r) – bd 0 z' = cn 1(u 1 t+p) + cn 2(u 2 t+q) + (d+cn 3)(u 3 t+r) – cd 0 h = n 1(u 1 t+p) + n 2(u 2 t+q) + n 3(u 3 t+r) – d 1

Generalized Projection § The vanishing point (xv, yv, zv) is obtained when t=α xu = (x‘/h) at t= α = a + (du 1/k) yu = b + (du 2/k) zu = c + (du 3/k) k = N. U = n 1 u 1 + n 2 u 2 + n 3 u 3 § If k=0 then ? § Principal vanishing point when U=I § xu = a + d / n 1, yu = b, zu = c, U=J U=k

Ref. § FV: p. 229 -237, 253 -258 § Sch: prob. 7. 1 – 7. 15 § Perspective Proj. pdf