Projectile Motion With Air Resistance Comparing the trajectory

2 Dimensional Motion Projectile motion is 2 dimensional motion in which objects moving horizontally

Ideal Projectiles The initial velocity of a projectile launched at an angle should be

Ideal Trajectory: • The parabolic trajectory can be modeled mathematically with simple algebra. •

Real Projectiles • Real projectiles experience air resistance – Consequences: • Actual X velocity

Drag Force Fdrag = drag force magnitude (N) d = drag coefficient (kg/m 3)

Drag Force on Projectiles Drag force can be represented as one 2 -dimensional vector

Drag Force on Projectiles This is the same baseball on the way down. Fd

You will now use a spreadsheet to… • Adjust the time increment to find

Troubleshooting/Tips • The actual range (with air resistance) will be at the top of

Slides: 10

Download presentation

Projectile Motion With Air Resistance Comparing the trajectory of an ideal projectile to that of one that experiences drag force.

2 Dimensional Motion Projectile motion is 2 dimensional motion in which objects moving horizontally while being accelerated vertically down by gravity • Recall: Vector components V Vy Vx

Ideal Projectiles The initial velocity of a projectile launched at an angle should be resolved into horizontal (X) and vertical (Y) components. Y X • Horizontal component of motion is constant velocity. • Vertical component of motion is uniformly accelerated.

Ideal Trajectory: • The parabolic trajectory can be modeled mathematically with simple algebra. • The range or horizontal displacement can be calculated by hand. • Air resistance is disregarded.

Real Projectiles • Real projectiles experience air resistance – Consequences: • Actual X velocity is not constant nor is X acceleration • Actual Y acceleration is not uniform. • As a result the real range is smaller and the shape of the trajectory is different than in the ideal case in which range is predicted without air resistance.

Drag Force Fdrag = drag force magnitude (N) d = drag coefficient (kg/m 3) CSA = cross sectional Area (m 2) v = velocity (m/s) Drag force is always opposite the direction of motion.

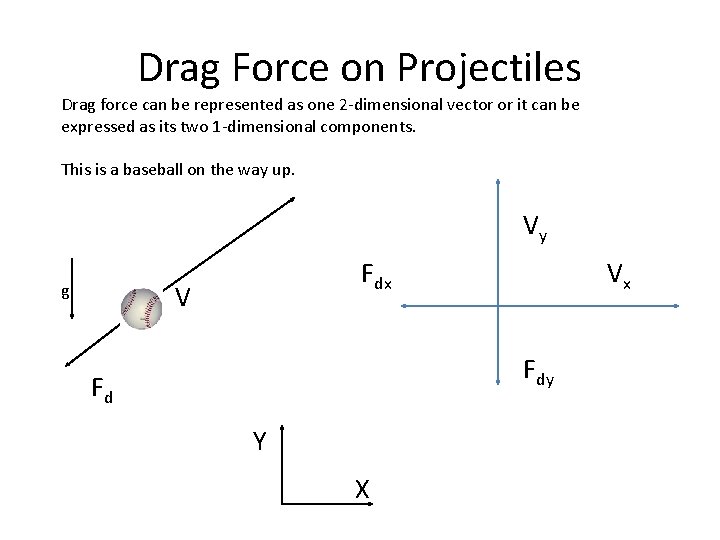
Drag Force on Projectiles Drag force can be represented as one 2 -dimensional vector or it can be expressed as its two 1 -dimensional components. This is a baseball on the way up. Vy Fdx V g Vx Fdy Fd Y X

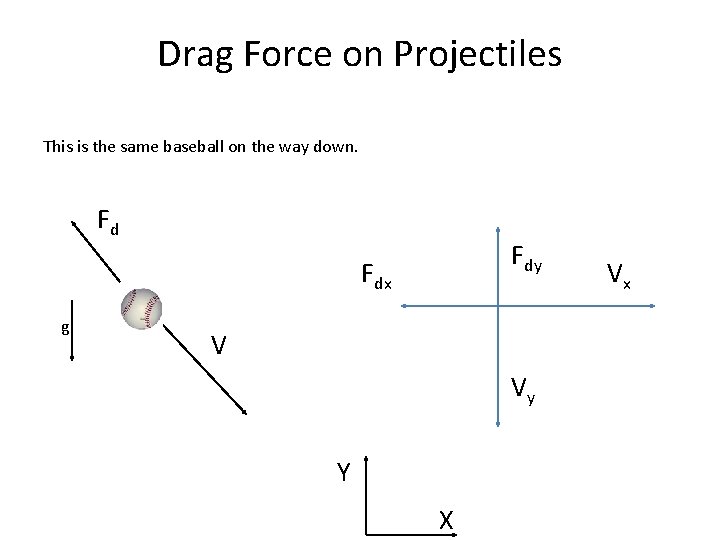
Drag Force on Projectiles This is the same baseball on the way down. Fd Fdy Fdx g V Vy Y X Vx

You will now use a spreadsheet to… • Adjust the time increment to find the range of a projectile experiencing air resistance. • Plot the ideal trajectory on the same axis as the real trajectory to compare their shapes. • Accurately predict the range of a projectile fired from a 16’’ cannon on the USS New Jersey.

Troubleshooting/Tips • The actual range (with air resistance) will be at the top of column O when it hits the ground (Y=0). To find the ideal range enter 0 for the drag factor (cell C 2) and look in the same place. • Highlight formulas as you write them into the spreadsheet. • Look at the equation that each formula is referring to in order to better understand its meaning. • Check each formula for accuracy after you have written it. Catching errors is going to save you some frustration if you need to search for a mistake.