Projectile Motion the motion of an object under

Projectile Motion - the motion of an object under the influence of gravity and inertia Trajectory – the path a projectile takes Range - the horizontal distance a projectile travels The motion is analyzed in the horizontal and vertical directions SEPARATELY!!

Accelerations in both directions are ALWAYS the same!!!! Vertical –> a = 9. 8 m/s 2 down Gravity is pulling a projectile down at all times Horizontal -> a = 0 Inertia keeps the object travelling with the same speed. There is no way it can speed up or slow down. (NAR)

Projectile Motion – Type 1 Projectiles that are initially moving horizontally Horizontal (0) and vertical (9. 8) accelerations are always known. Vertical initial velocity = 0

A stone is thrown horizontally at a speed of 5 m/s from the top of a cliff 78. 4 m high. a)How far from the base of the cliff does the stone hit the ground? b)What are the horizontal and vertical components of the stone’s velocity before it hits the ground?

A plane is flying horizontally at 115 m/s and must drop cargo that will land on an island that is 1000 m ahead horizontally. a)How high must the plane be when it drops its cargo? b) How fast is it going when it hits the ground?

A steel ball rolls with constant velocity across a tabletop 0. 95 m high. It rolls off and hits the ground 0. 352 m from the edge of the table. How fast was the ball rolling? (What was its horizontal vi? )

You take a running horizontal leap off a high-diving platform. You were running at 2. 8 m/s and hit the water 2. 6 s later. How high was the platform and how far out did you hit the water?

An arrow is fired horizontally with a speed of 30 m/s. The arrow drops 0. 5 m before striking the target. What is the range of the target?

Projectile Motion – Type 2 Projectiles that are initially moving DIAGONALLY. As in ALL proj mots, horizontal (0) and vertical (9. 8) accelerations are always known.

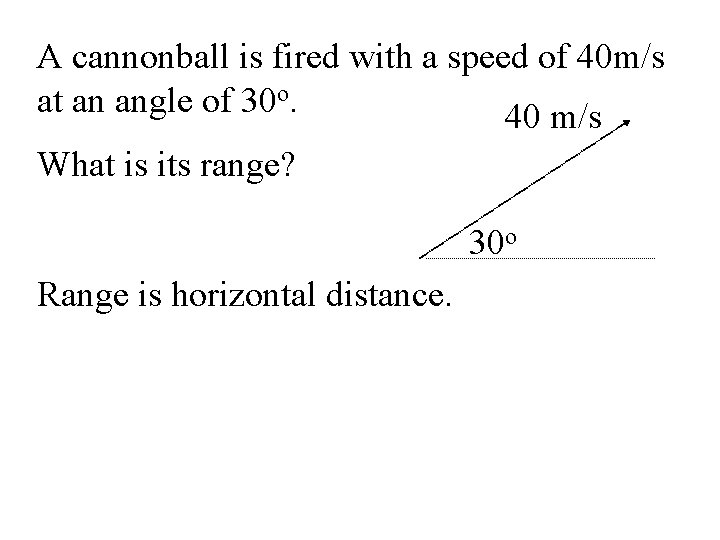
A cannonball is fired with a speed of 40 m/s at an angle of 30 o. 40 m/s What is its range? 30 o Range is horizontal distance.

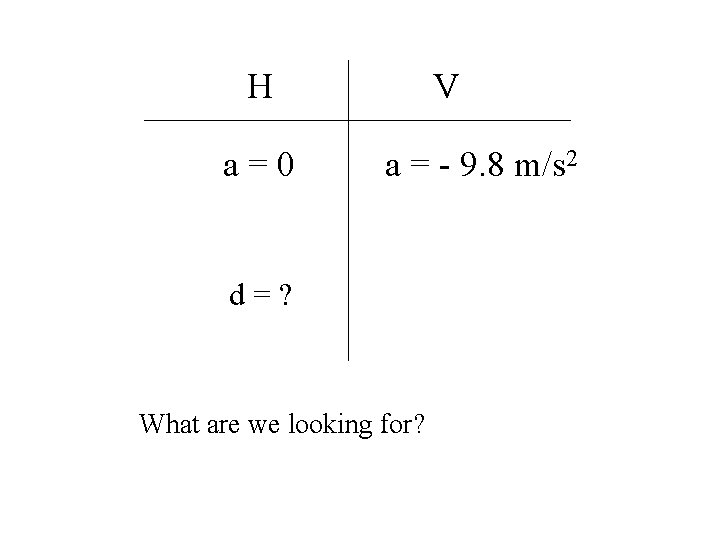
H a=0 V a = - 9. 8 m/s 2 d=? What are we looking for?

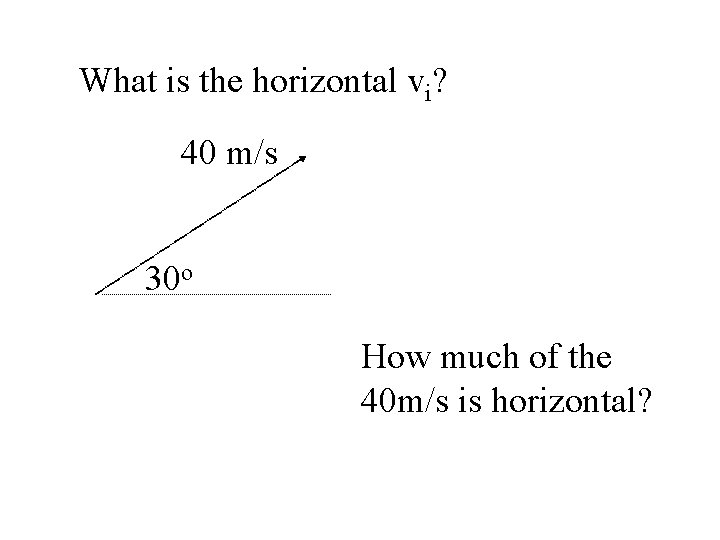
What is the horizontal vi? 40 m/s 30 o How much of the 40 m/s is horizontal?

Equations used to find the components of a vector: Ax = A cos q q = angle of vector A = magnitude of vector 40 m/s Ax = horizontal component of vector A 30 o

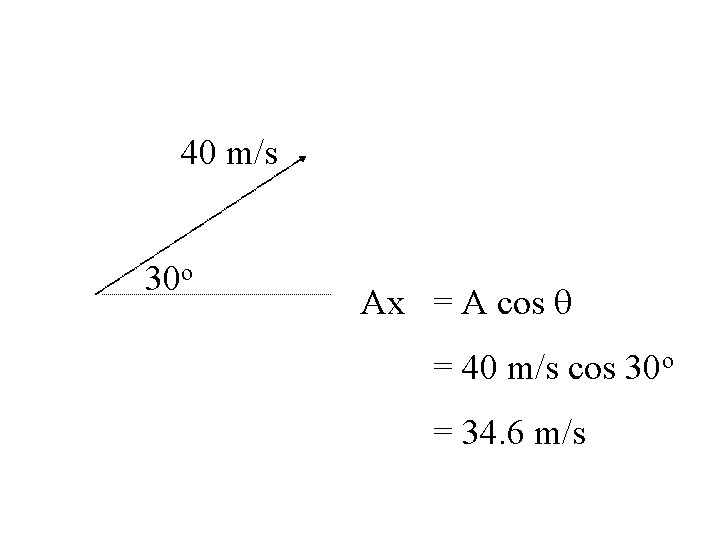
40 m/s 30 o Ax = A cos q = 40 m/s cos 30 o = 34. 6 m/s

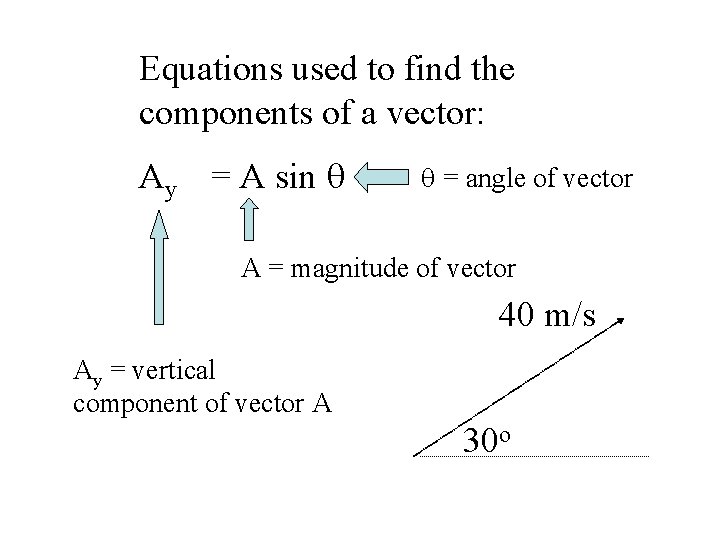
Equations used to find the components of a vector: Ay = A sin q q = angle of vector A = magnitude of vector 40 m/s Ay = vertical component of vector A 30 o

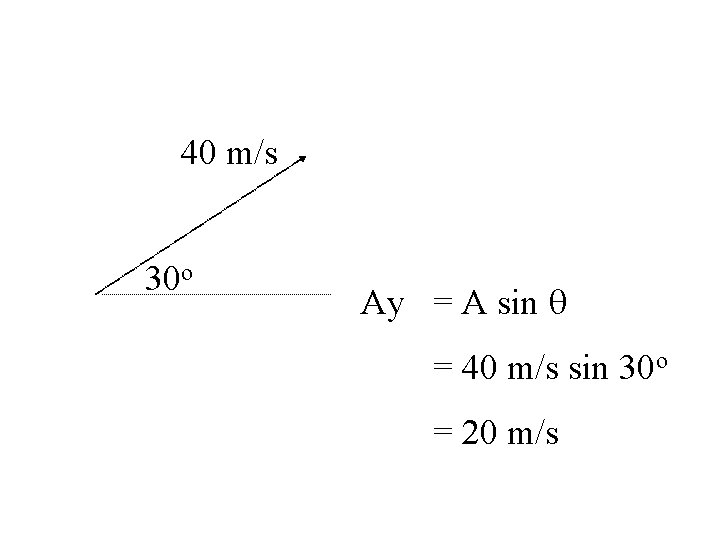
40 m/s 30 o Ay = A sin q = 40 m/s sin 30 o = 20 m/s

Equations for finding horizontal vi: Ax = A cos q Equations for finding vertical vi: Ay = A sin q

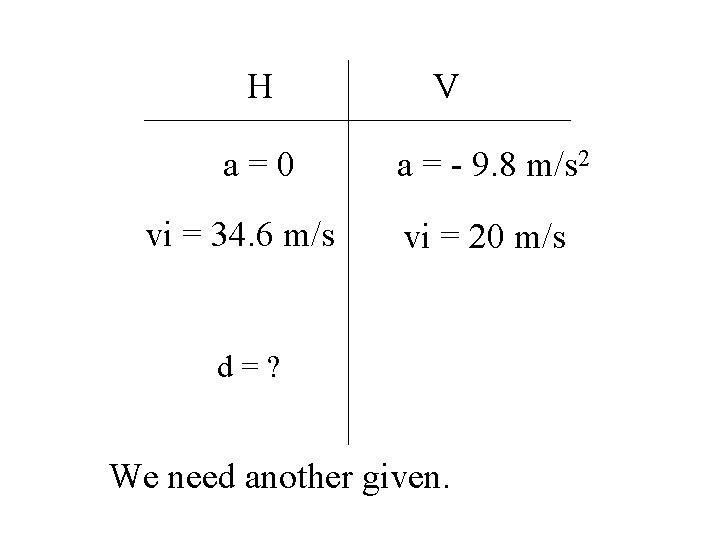
H a=0 vi = 34. 6 m/s V a = - 9. 8 m/s 2 vi = 20 m/s d=? We need another given.

What else do we know about this motion? What is its final vertical displacement (height)?

H a=0 vi = 34. 6 m/s V a = - 9. 8 m/s 2 vi = 20 m/s d=0 d=? Time to go BUCK WILD!!!

How high does this projectile go?

A motorcycle leaves a 45 o ramp going 25 m/s. How far does it travel horizontally? How high does it go?

Proj Mot Summary

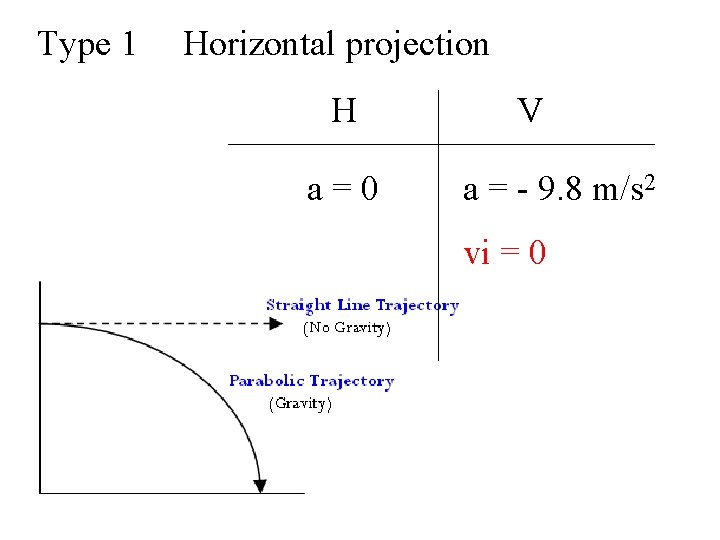
Type 1 Horizontal projection H a=0 V a = - 9. 8 m/s 2 vi = 0

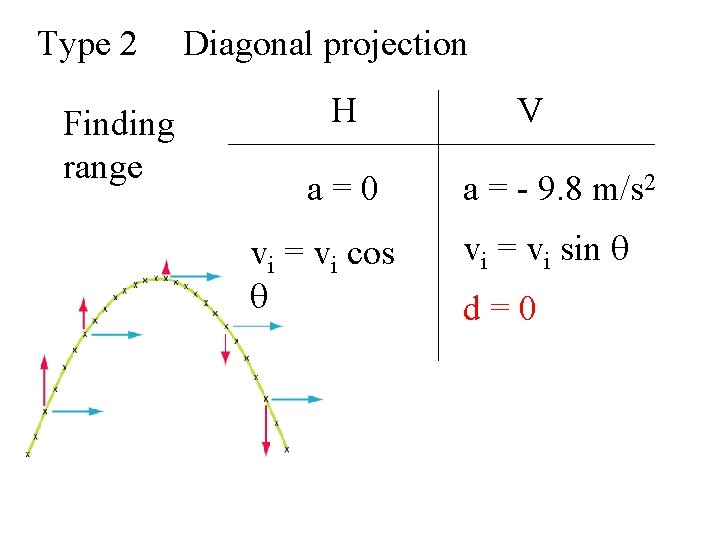
Type 2 Finding range Diagonal projection H a=0 vi = vi cos q V a = - 9. 8 m/s 2 vi = vi sin q d=0

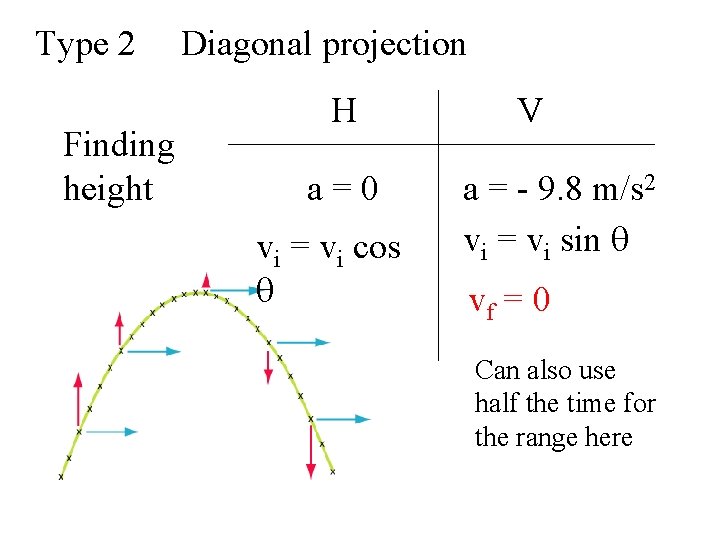
Type 2 Finding height Diagonal projection H a=0 vi = vi cos q V a = - 9. 8 m/s 2 vi = vi sin q vf = 0 Can also use half the time for the range here

A cannonball is shot at 37 o above the horizontal. Its velocity is 100 m/s and it hits a target on level ground. How far away is the target? H a=0 vi = 80 m/s t = 12. 2 s d = 980 m V a = - 9. 8 m/s 2 vi = 60 m/s d=0 t = 12. 2 s

A cannonball is shot at 37 o above the horizontal. Its velocity is 100 m/s and it hits a target on level ground. What is the maximum height the cannonball will attain? H a=0 vi = 80 m/s V a = - 9. 8 m/s 2 vi = 60 m/s vf = 0 m/s d = 184 m

A car drives off a horizontal cliff. It was driving at 45 m/s and hits the water 4. 1 s later. How high was the cliff and how far out did it hit the water? H a=0 vi = 45 m/s t = 4. 1 m/s d = 184. 5 m V a = - 9. 8 m/s 2 vi = 0 m/s t = 4. 1 m/s d = 82. 4 m