PROJECTILE MOTION Projectile Motion FThe path that a

PROJECTILE MOTION

Projectile Motion FThe path that a moving object follows is called its trajectory. FProjectile motion involves the trajectories and velocities of any object that has been launched, shot, or thrown.

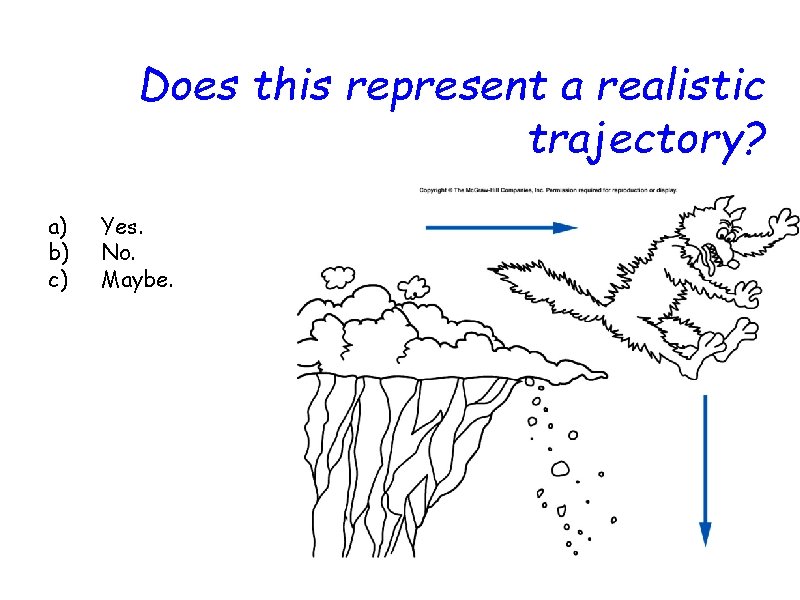
Does this represent a realistic trajectory? a) b) c) Yes. No. Maybe.

Does this represent a realistic trajectory?

Does this represent a realistic trajectory? a) b) c) Yes. No. Maybe. The coyote would not go straight horizontally, pause, and then fall straight down. You see unrealistic trajectories all the time in media. Can you think of any others?

RULES There are only a few rules we have to follow: All projectiles are freefalling vertically with an acceleration of 9. 8 m/s 2 downwards Horizontal motion is totally unaffected by gravity! Since there are no forces acting on it, a falling object’s horizontal velocity is constant!

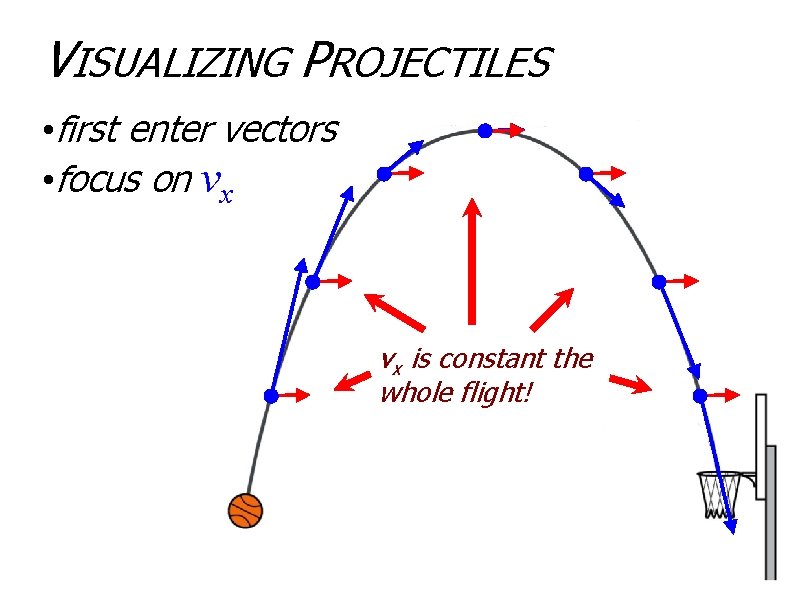
VISUALIZING PROJECTILES • first enter vectors • focus on vx vx is constant the whole flight!

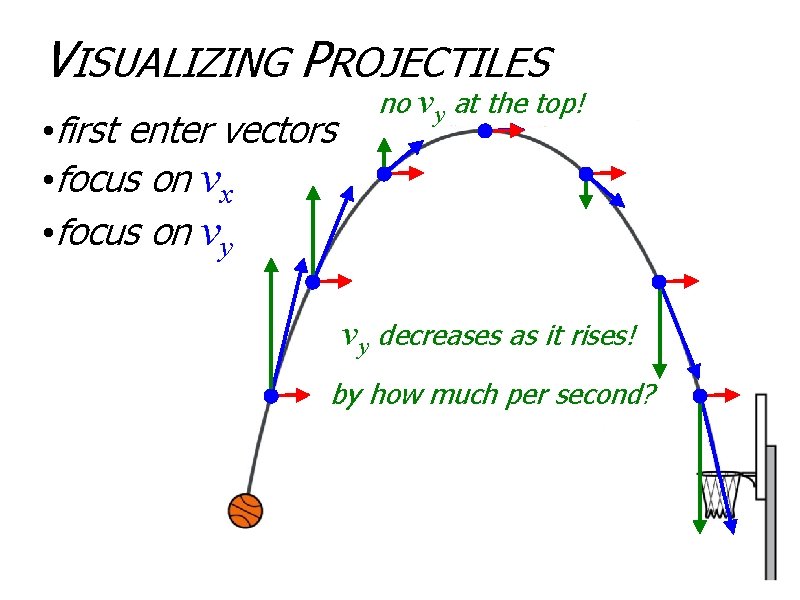
VISUALIZING PROJECTILES • first enter vectors • focus on vx • focus on vy no vy at the top! vy decreases as it rises! by how much per second?

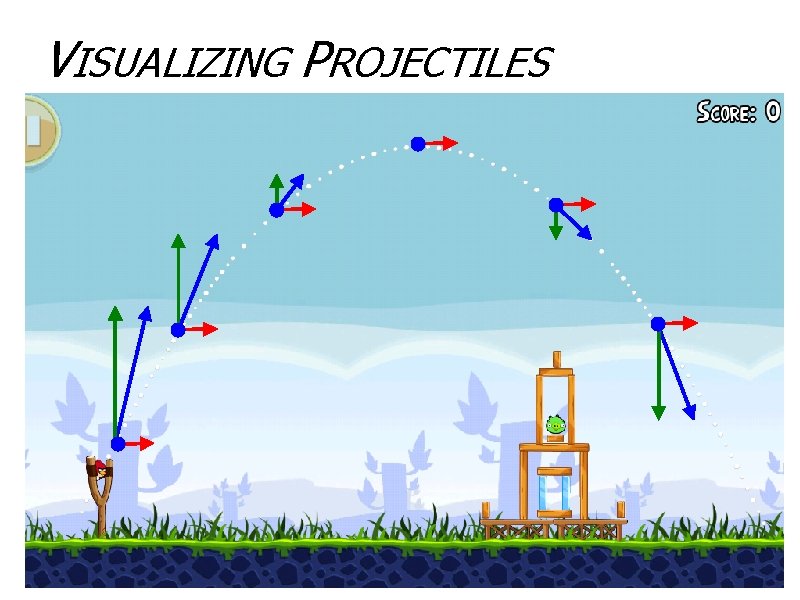
VISUALIZING PROJECTILES

X equations Y equations 0

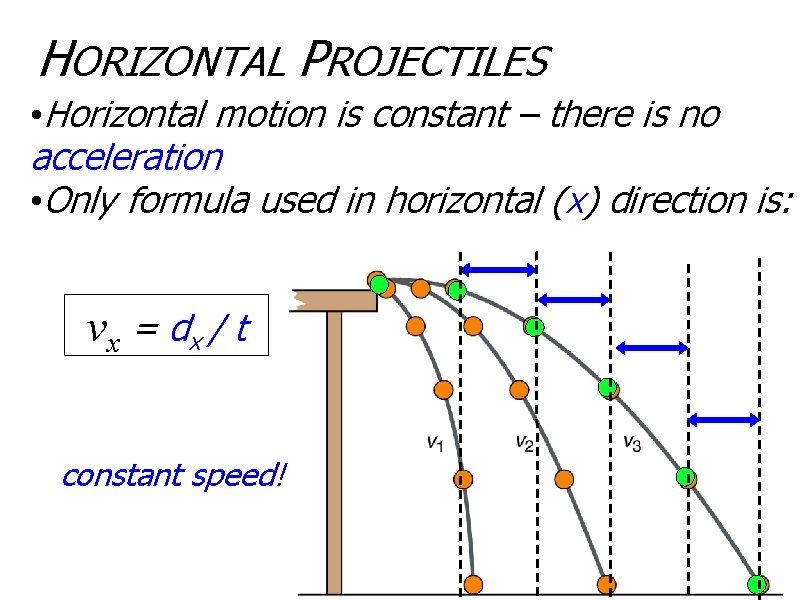
HORIZONTAL PROJECTILES • Horizontal motion is constant – there is no acceleration • Only formula used in horizontal (x) direction is: v x = dx / t constant speed!

HORIZONTAL PROJECTILES • Horizontal projectiles are not thrown up or down. They are moving horizontally and falling vertically • The only initial velocity is in the x direction • Vertical velocity (vy) is gained by freefall • viy = 0 • since viy is in freefall, • a = -9. 8 m/s 2

HORIZONTAL PROJECTILE pg 288 1. A rock is thrown horizontally from the top of a cliff at a constant speed of 15 m/s. Calculate the horizontal & vertical positions of the rock after each second and place these positions in the table below. Assume the rock is freefalling from rest.

ANGLED PROJECTILE pg 289 A rock is thrown at an angle of 30° from the top of a cliff. Calculate the horizontal & vertical positions of the rock after each second and place these positions in the table below.

X equations Y equations

LET’S ANALYZE THE JUMP dmax 1. Measure his height, Find the scale of the picture.

LET’S ANALYZE THE JUMP

Variable Definitions: vyi initial velocity in y direction vx = constant velocity in x direction v final velocity of projectile dx horizontal range dy Height dy Maximum altitude dy Vertical displacement

Hitting a Target ØIf the rifle is fired directly at the target in a horizontal direction, will the bullet hit the center of the target? ØDoes the bullet fall during its flight?

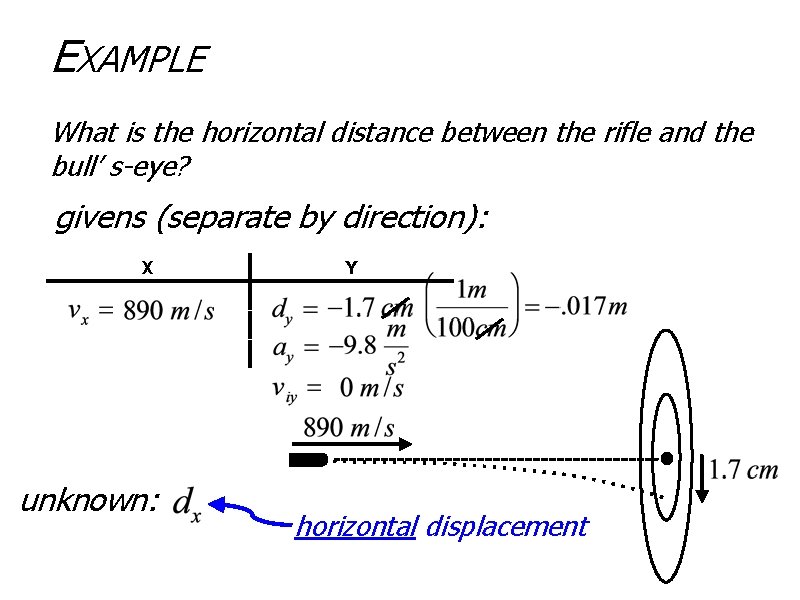
EXAMPLE A person decides to fire a rifle horizontally at a bull’s-eye. The speed of the bullet as it leaves the barrel of the gun is 890 m/s. He’s new to the ideas of projectile motion so doesn’t aim high and the bullet strikes the target 1. 7 cm below the center of the bull’s-eye. What is the horizontal distance between the rifle and the bull’ s-eye? start by drawing a picture: label the explicit givens with subscript. Ex: dx or dy

EXAMPLE What is the horizontal distance between the rifle and the bull’ s-eye? givens (separate by direction): X unknown: Y horizontal displacement

EXAMPLE which equation do we use? use rewrite equation for t to find time

EXAMPLE Use t and vx to solve for dx

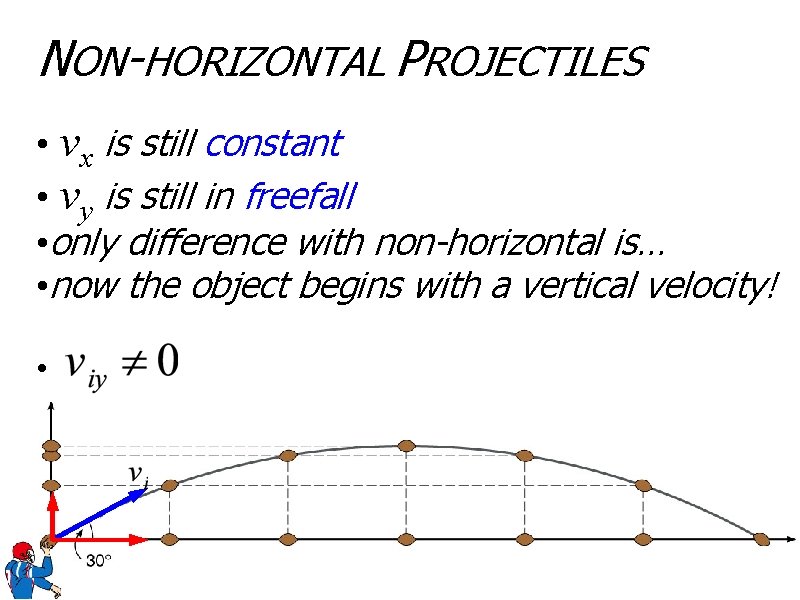
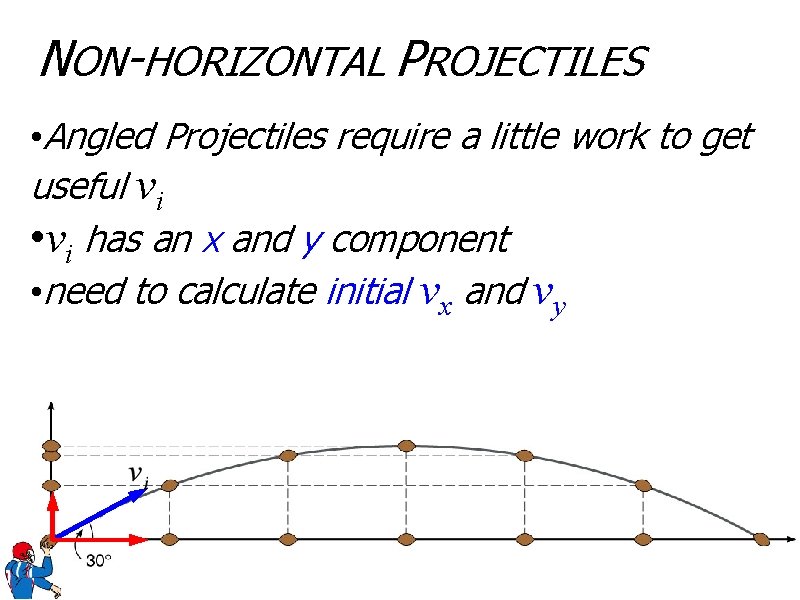
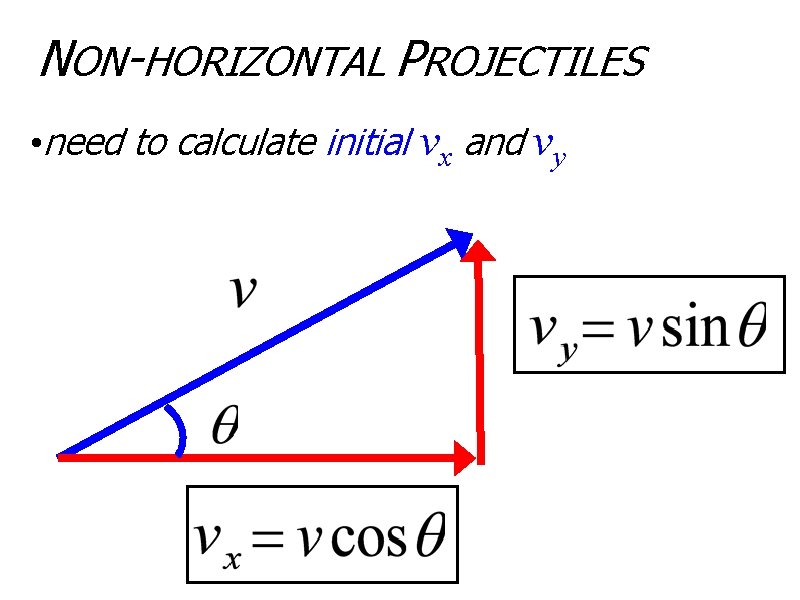
NON-HORIZONTAL PROJECTILES • vx is still constant • vy is still in freefall • only difference with non-horizontal is… • now the object begins with a vertical velocity! •

NON-HORIZONTAL PROJECTILES • Angled Projectiles require a little work to get useful vi • vi has an x and y component • need to calculate initial vx and vy

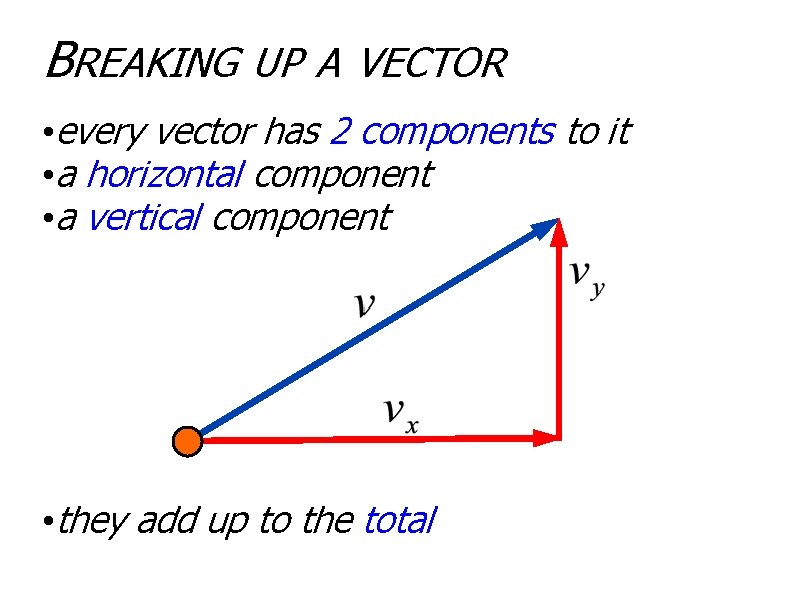
BREAKING UP A VECTOR • every vector has 2 components to it • a horizontal component • a vertical component • they add up to the total

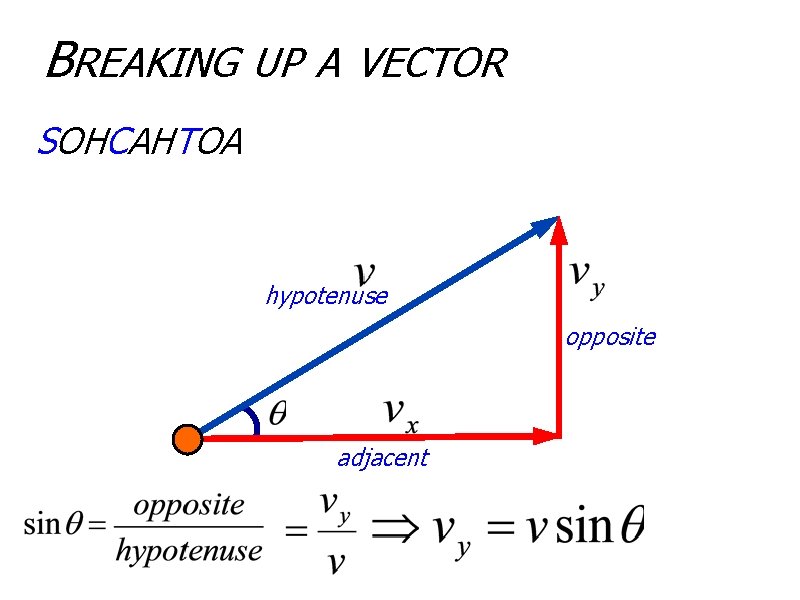
BREAKING UP A VECTOR SOHCAHTOA hypotenuse opposite adjacent

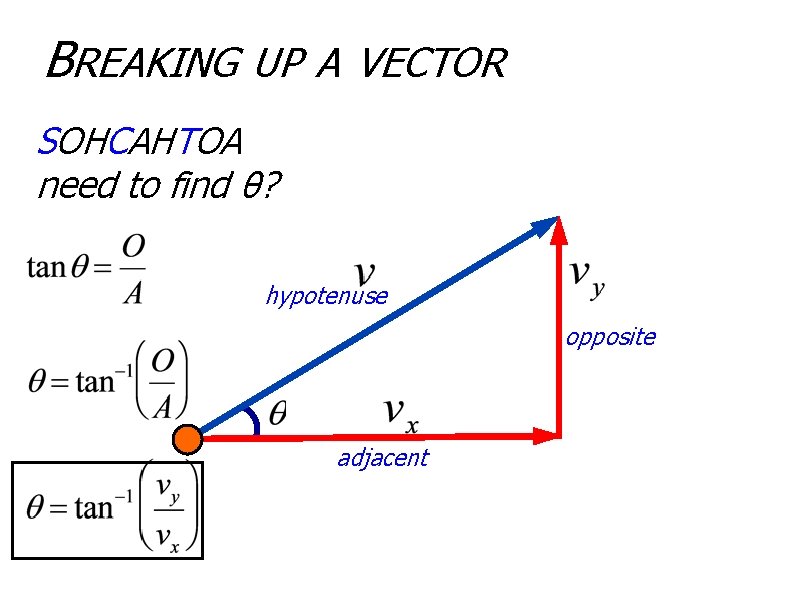
BREAKING UP A VECTOR SOHCAHTOA need to find θ? hypotenuse opposite adjacent

NON-HORIZONTAL PROJECTILES • need to calculate initial vx and vy

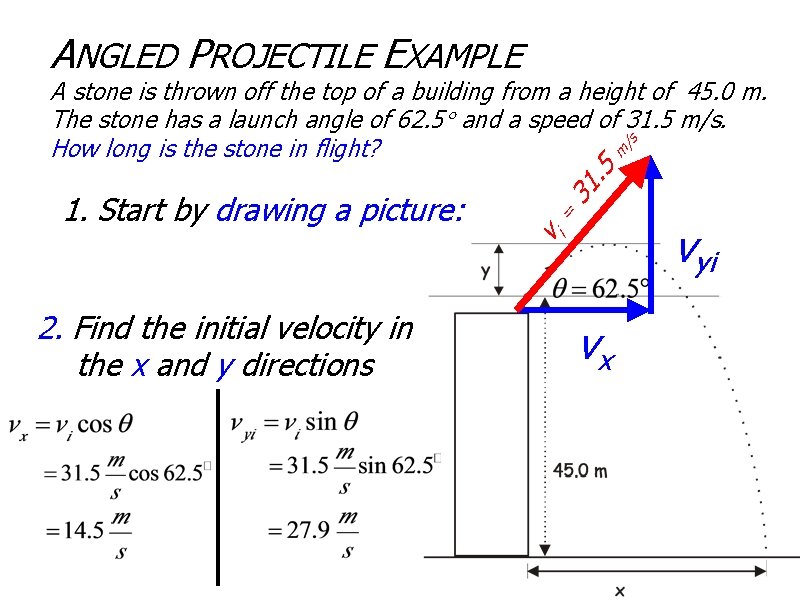
ANGLED PROJECTILE EXAMPLE A stone is thrown off the top of a building from a height of 45. 0 m. The stone has a launch angle of 62. 5 and a speed of 31. 5 m/s. /s How long is the stone in flight? m 1. Start by drawing a picture: 2. Find the initial velocity in the x and y directions vi = 3 5. 1 vx vyi

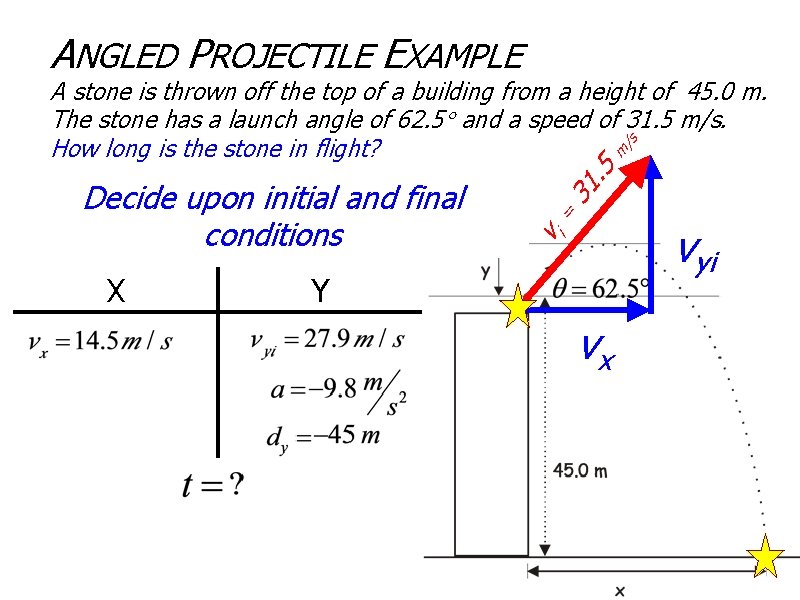
ANGLED PROJECTILE EXAMPLE A stone is thrown off the top of a building from a height of 45. 0 m. The stone has a launch angle of 62. 5 and a speed of 31. 5 m/s. /s How long is the stone in flight? m Decide upon initial and final conditions X vi = 3 5. 1 Y vx vyi

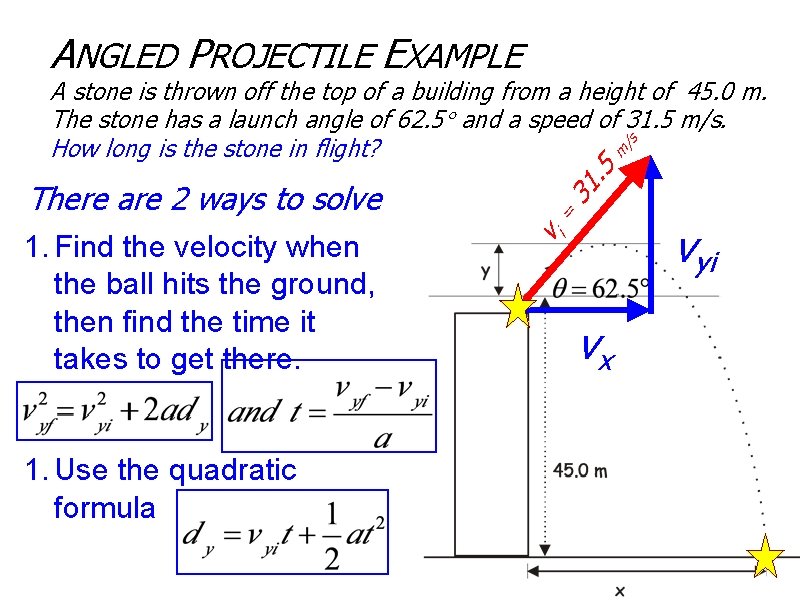
ANGLED PROJECTILE EXAMPLE A stone is thrown off the top of a building from a height of 45. 0 m. The stone has a launch angle of 62. 5 and a speed of 31. 5 m/s. /s How long is the stone in flight? m There are 2 ways to solve 1. Find the velocity when the ball hits the ground, then find the time it takes to get there. 1. Use the quadratic formula vi = 3 5. 1 vx vyi

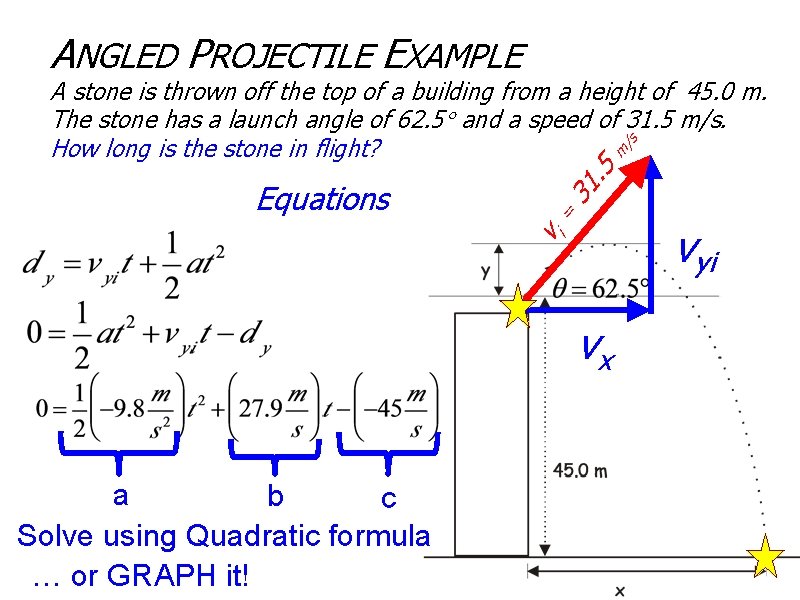
ANGLED PROJECTILE EXAMPLE A stone is thrown off the top of a building from a height of 45. 0 m. The stone has a launch angle of 62. 5 and a speed of 31. 5 m/s. /s How long is the stone in flight? m Equations vi = 3 5. 1 vx a b c Solve using Quadratic formula … or GRAPH it! vyi

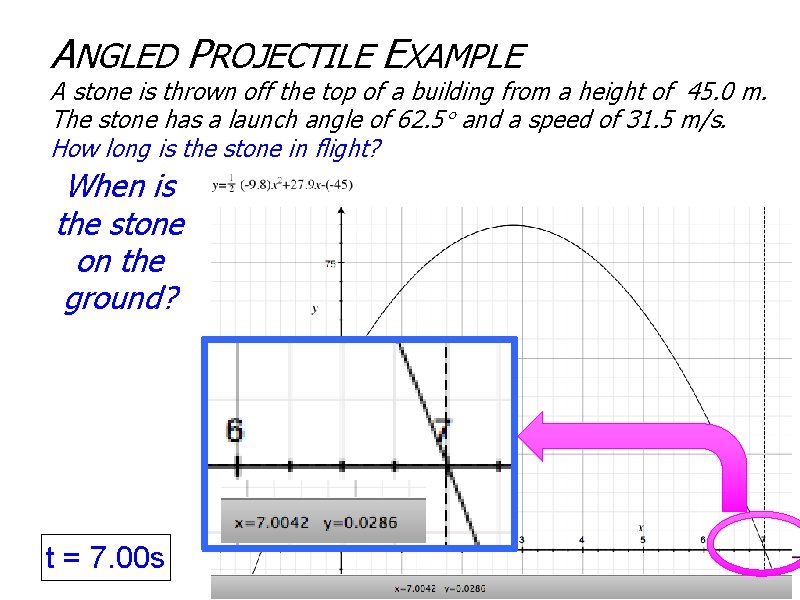
ANGLED PROJECTILE EXAMPLE A stone is thrown off the top of a building from a height of 45. 0 m. The stone has a launch angle of 62. 5 and a speed of 31. 5 m/s. How long is the stone in flight? When is the stone on the ground? t = 7. 00 s = /s v o 5 m. 1 3 vx vyo

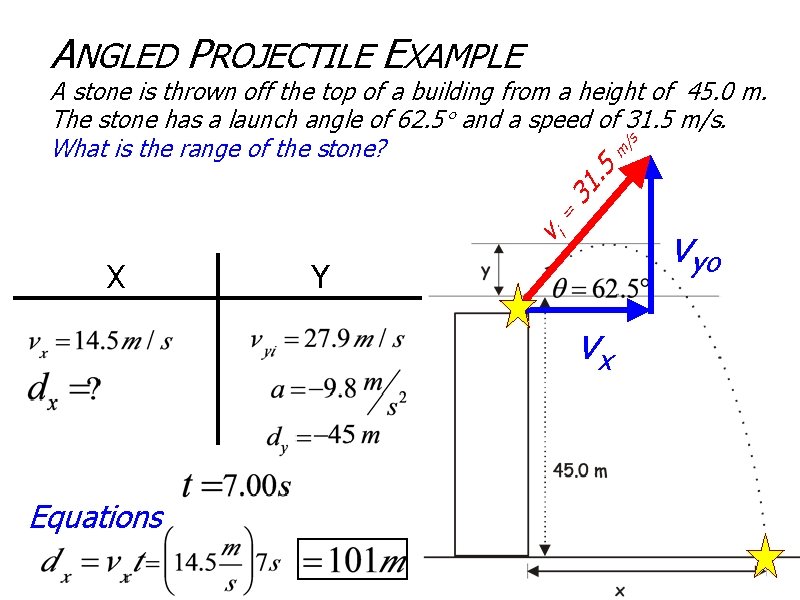
ANGLED PROJECTILE EXAMPLE A stone is thrown off the top of a building from a height of 45. 0 m. The stone has a launch angle of 62. 5 and a speed of 31. 5 m/s. /s What is the range of the stone? m vi X = 3 5. 1 Y vx Equations vyo

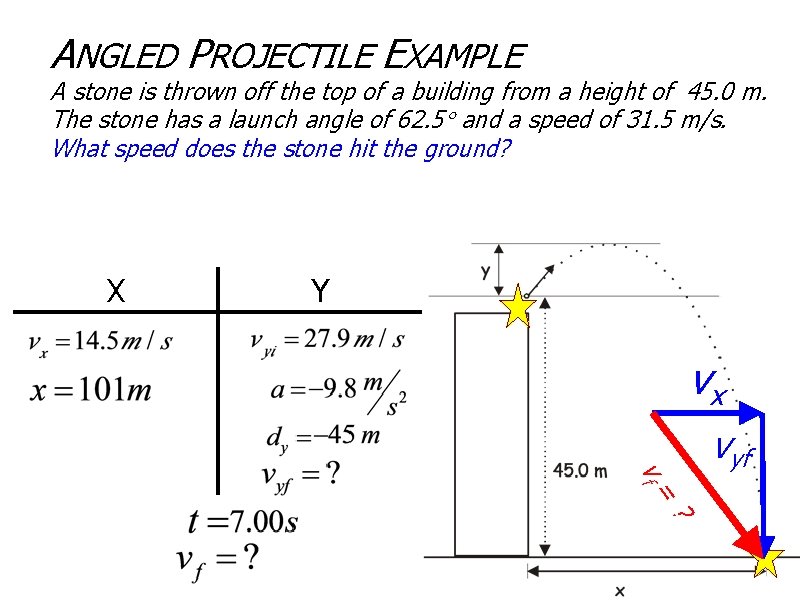
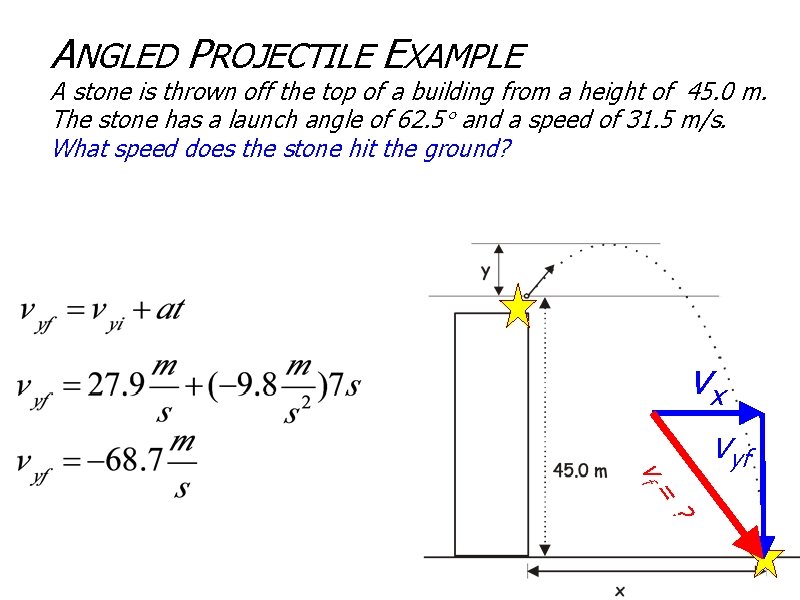
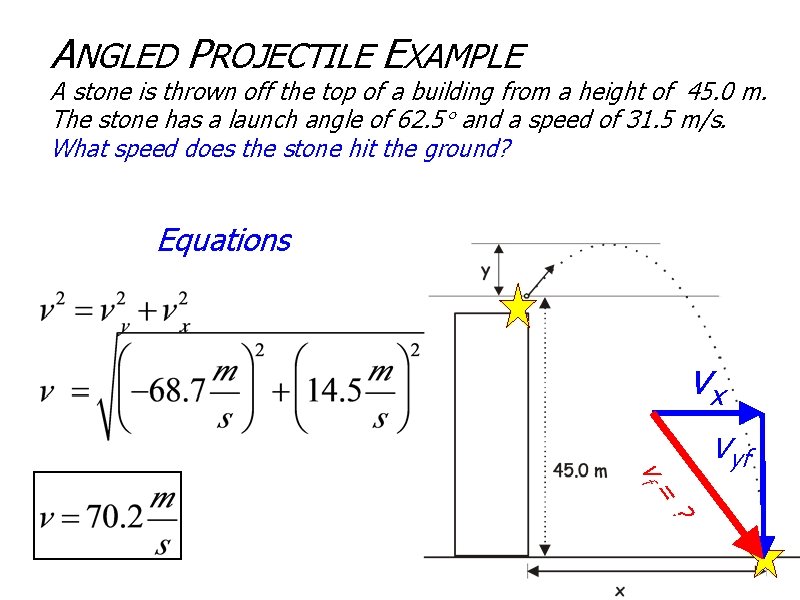
ANGLED PROJECTILE EXAMPLE A stone is thrown off the top of a building from a height of 45. 0 m. The stone has a launch angle of 62. 5 and a speed of 31. 5 m/s. What speed does the stone hit the ground? X Y vx vf vyf = ?

ANGLED PROJECTILE EXAMPLE A stone is thrown off the top of a building from a height of 45. 0 m. The stone has a launch angle of 62. 5 and a speed of 31. 5 m/s. What speed does the stone hit the ground? vx vf vyf = ?

ANGLED PROJECTILE EXAMPLE A stone is thrown off the top of a building from a height of 45. 0 m. The stone has a launch angle of 62. 5 and a speed of 31. 5 m/s. What speed does the stone hit the ground? Equations. Givens vx vf vyf = ?

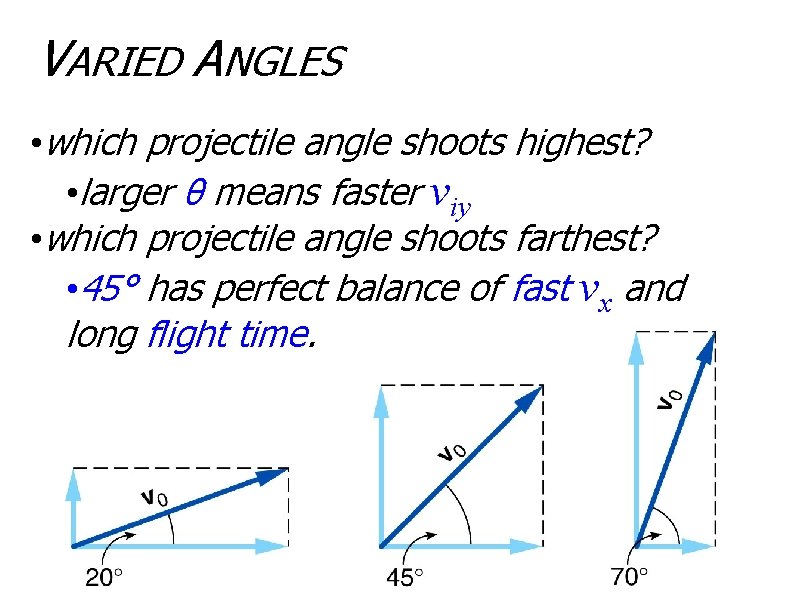
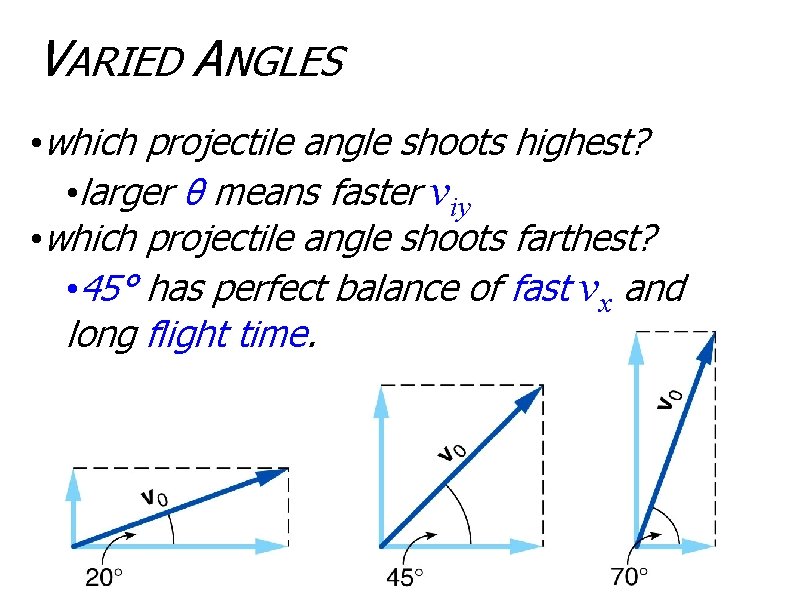
VARIED ANGLES • which projectile angle shoots highest? • larger θ means faster viy • which projectile angle shoots farthest? • 45° has perfect balance of fast vx and long flight time.

PRACTICE PG 298

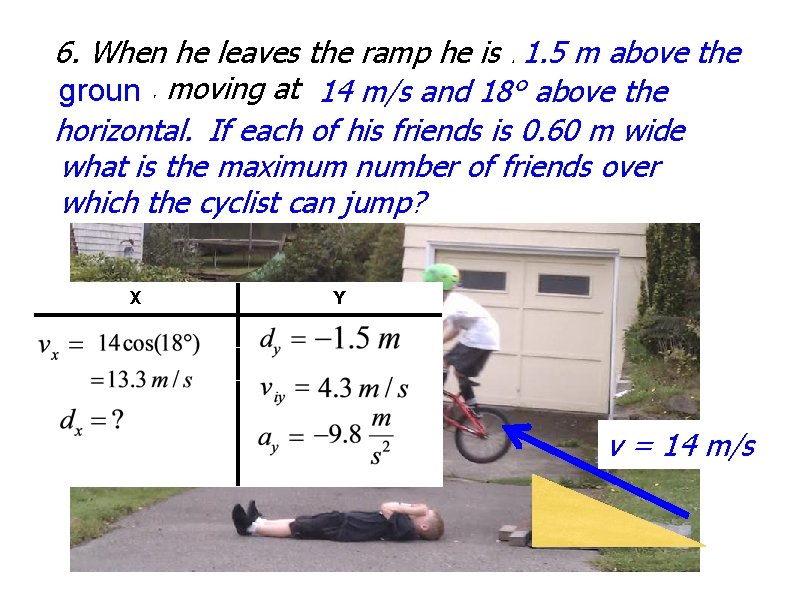
6. When he leaves the ramp he is 1. 5 mmabovethe ground, groun moving at 14 14 m/s m/sand 18° 18°abovethe horizontal. If each d horizontal. each of of his friends isis 0. 60 m m wide, wide what isis the maximum number of of friends over which the cyclist can jump? X Y v = 14 m/s

When he leaves the ramp he is 1. 5 m above the ground, moving at 14 m/s and 18° above the horizontal. If each of his friends is 0. 60 m wide, what is the maximum number of friends over which the cyclist can jump? X Y 1. Find t which equation do we use? We could use to find time But you would have to use the quadratic formula to solve for t because there is a t and t 2

When he leaves the ramp he is 1. 5 m above the ground, moving at 14 m/s and 18° above the horizontal. If each of his friends is 0. 60 m wide, what is the maximum number of friends over which the cyclist can jump? X Y 1. Find t which equation do we use? Instead, find vyf And then find t: vyf = - 6. 9 m/s t = 1. 14 s

When he leaves the ramp he is 1. 5 m above the ground, moving at 14 m/s and 18° above the horizontal. If each of his friends is 0. 60 m wide, what is the maximum number of friends over which the cyclist can jump? X Y vyf = - 6. 9 m/s t = 1. 14 s 3. How many friends? 2. Find dx

VARIED ANGLES • which projectile angle shoots highest? • larger θ means faster viy • which projectile angle shoots farthest? • 45° has perfect balance of fast vx and long flight time.

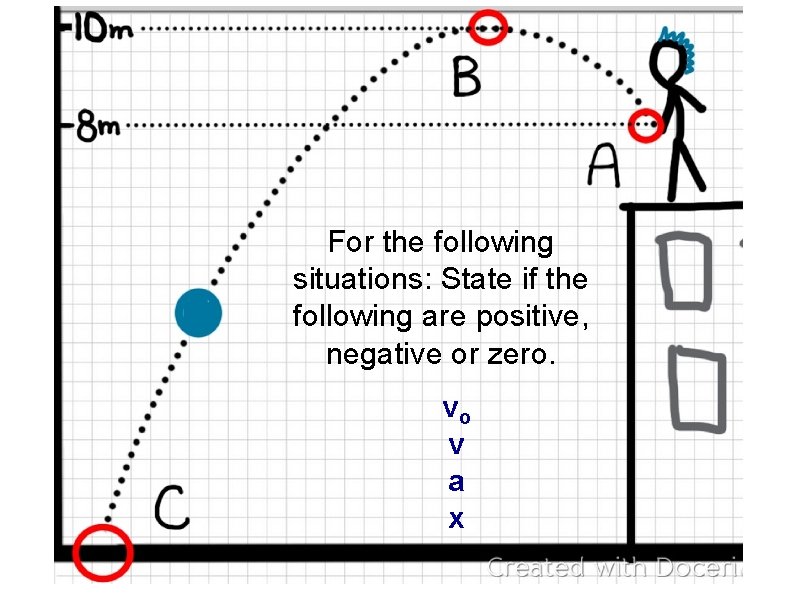
` For the following situations: State if the following are positive, negative or zero. vo v a x

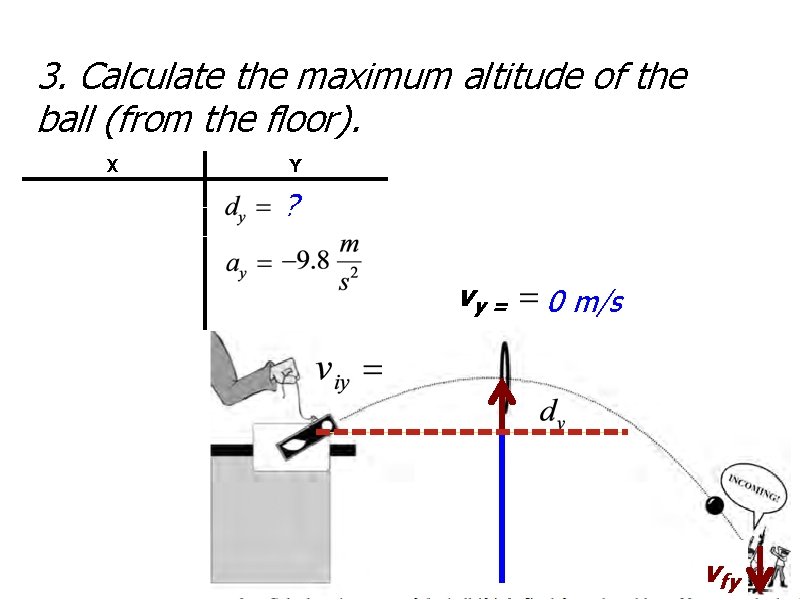
3. Calculate the maximum altitude of the ball (from the floor). X Y ? vvyfy= 0 m/s vfy

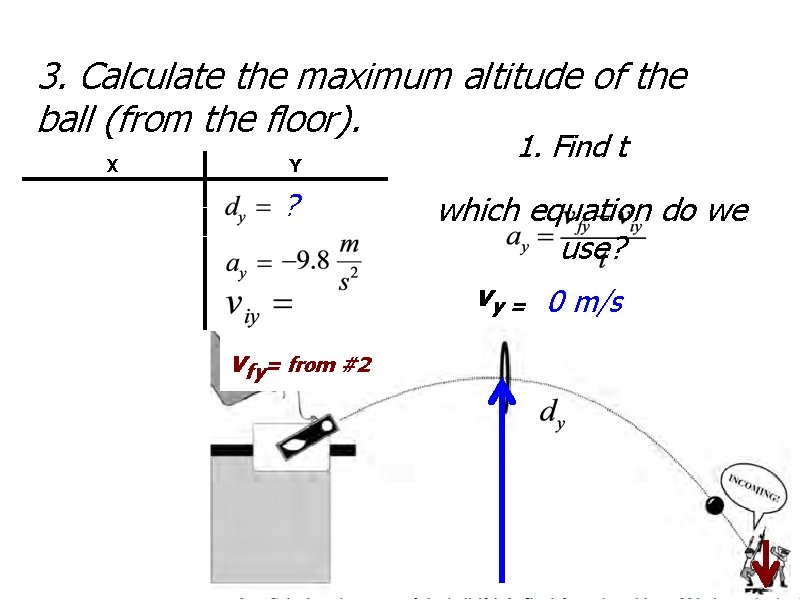
3. Calculate the maximum altitude of the ball (from the floor). X Y ? 1. Find t which equation do we use? vy = 0 m/s vfy= from #2

Percent Error Formula, last pg of text *Known = your calculation