Projectile Motion Part 2 projectiles launched at an

Projectile Motion: Part 2 (projectiles launched at an angle)

Vertical Launch Caused by: • Sending something into the air at an angle • Still has horizontal and vertical components that are independent of each other, but related by time (as in horizontal launch) • Can be represented as triangle

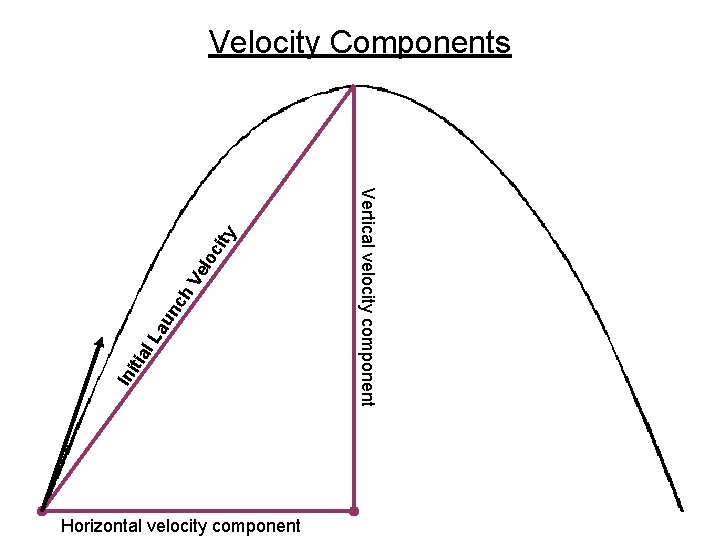
cit lo Ve h nc au al L iti In Horizontal velocity component Vertical velocity component y Velocity Components

Velocity Components • Horizontal velocity: – Is constant for the duration of the objects’ trip ( V in θ Vhorizontal (v. H) Vvertical (vv) al iti v )i Can be calculated by: cos θ = v. H / vi v. H = (cos θ)(vi)

Velocity Components • Vertical velocity: – Is constantly accelerated in the negative direction by gravity (-9. 8 m/s 2) ( V in θ Vhorizontal (v. H) Vvertical (vv) al iti v )i Can be calculated by: sin θ = vv / vi vv = (sin θ)(vi)

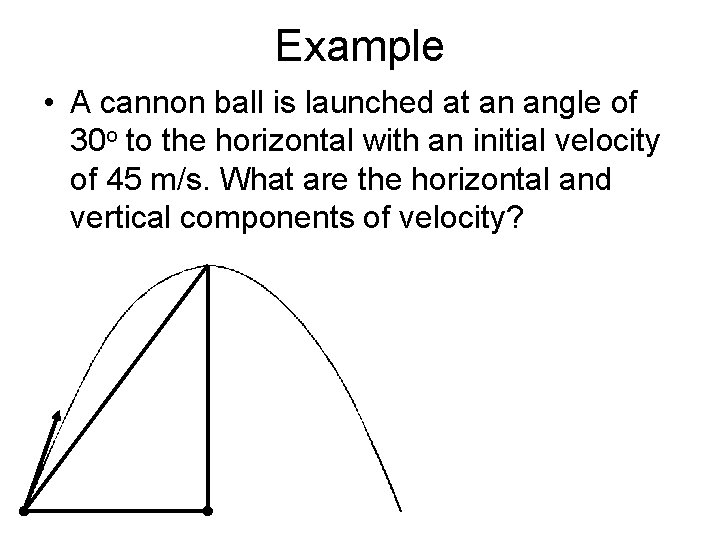
Example • A cannon ball is launched at an angle of 30 o to the horizontal with an initial velocity of 45 m/s. What are the horizontal and vertical components of velocity?

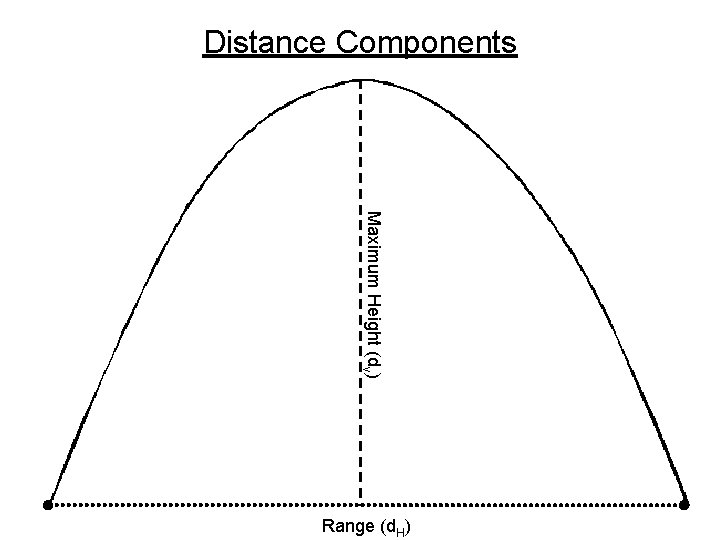
Distance Components Maximum Height (dv) Range (d. H)

Distance Components • Vertical Distance: the maximum height the projectile reaches during travel Can be calculated like a free fall problem: dv= at 2/2 (Often becomes a two part problem using a given initial velocity)

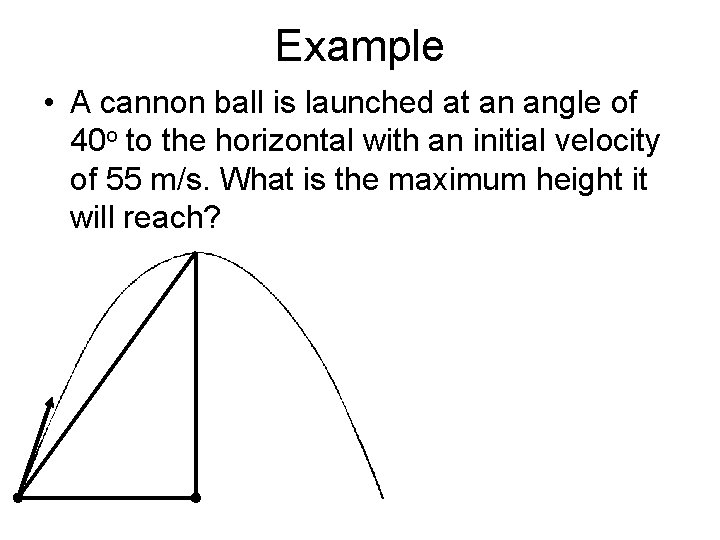
Example • A cannon ball is launched at an angle of 40 o to the horizontal with an initial velocity of 55 m/s. What is the maximum height it will reach?

Distance Components • Horizontal Distance: the maximum range the projectile will travel Can be calculated using linear motion equations: v. H = d. H/t d. H = (v. H)(t) (Often becomes a two-three part problem using a given initial velocity)

Example • A cannon ball is launched at an angle of 40 o to the horizontal with an initial velocity of 55 m/s. What is its maximum range?