Projectile Motion Horizontally Launched Projectiles which have NO

Projectile Motion

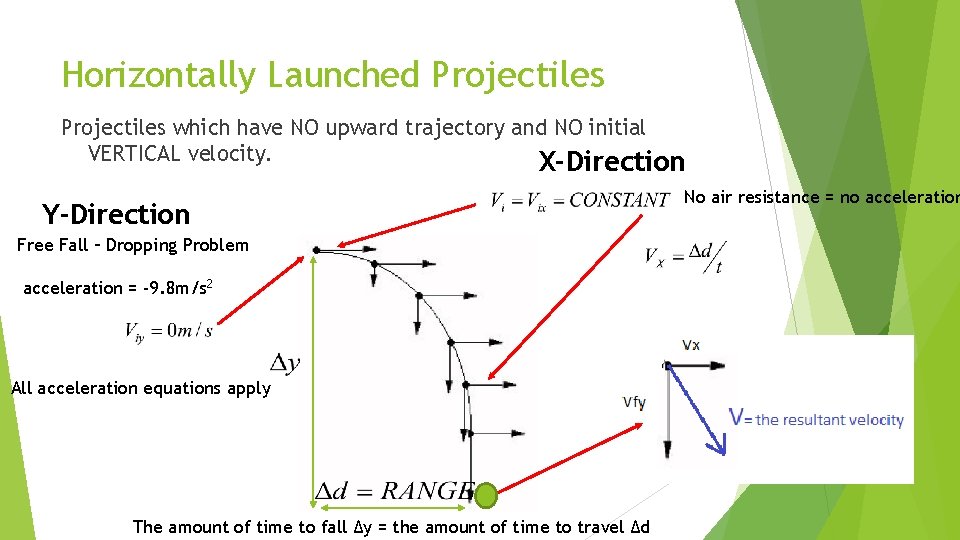
Horizontally Launched Projectiles which have NO upward trajectory and NO initial VERTICAL velocity. X-Direction Y-Direction Free Fall – Dropping Problem acceleration = -9. 8 m/s 2 All acceleration equations apply The amount of time to fall ∆y = the amount of time to travel ∆d No air resistance = no acceleration

Class Demo: Arrow Launcher

Example: In movies, you often see people jump from one building roof to another. If a person were to jump from a roof with a speed of 2. 5 m/s and the roof he wants to land on is 3. 5 m away and is 4. 5 m lower than the roof is jumping from, will he make it to the other roof?

Projectiles Launched At An Angle Y-Direction Since the projectile was launched at a angle, the velocity MUST be broken into components!!! X-Direction vi viy Free Fall – Up and Down Problem acceleration = -9. 8 m/s 2 q vix

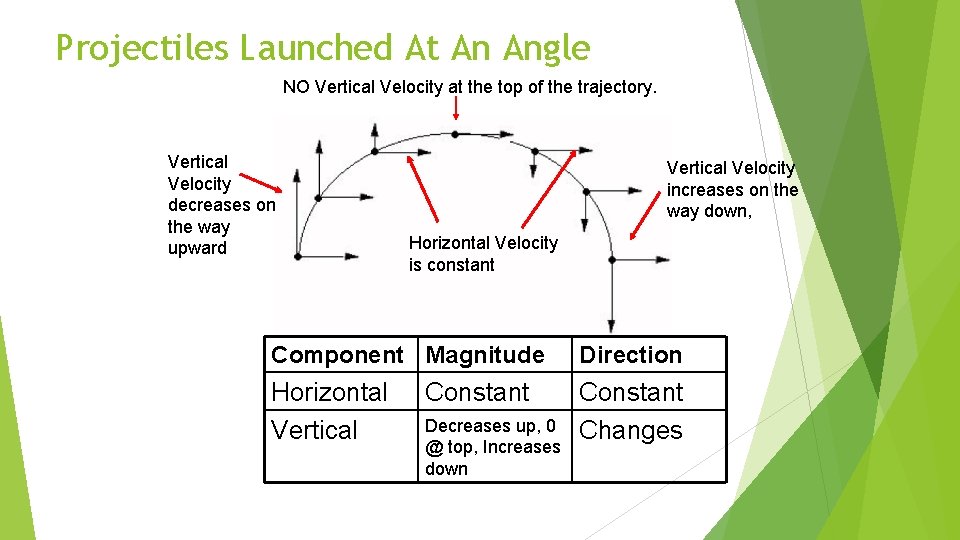
Projectiles Launched At An Angle NO Vertical Velocity at the top of the trajectory. Vertical Velocity decreases on the way upward Vertical Velocity increases on the way down, Horizontal Velocity is constant Component Magnitude Direction Horizontal Vertical Constant Changes Constant Decreases up, 0 @ top, Increases down

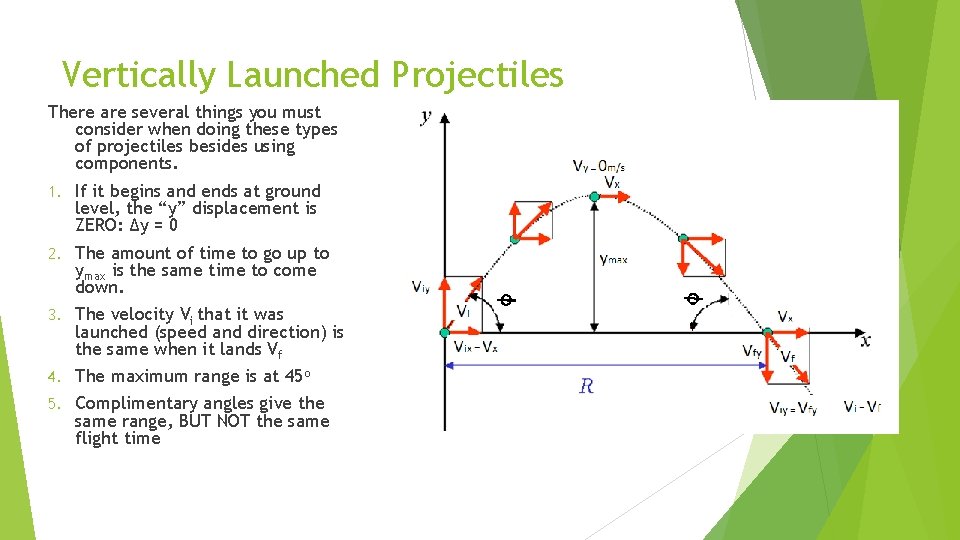
Vertically Launched Projectiles There are several things you must consider when doing these types of projectiles besides using components. 1. If it begins and ends at ground level, the “y” displacement is ZERO: ∆y = 0 2. The amount of time to go up to ymax is the same time to come down. 3. The velocity Vi that it was launched (speed and direction) is the same when it lands Vf 4. The maximum range is at 45 o 5. Complimentary angles give the same range, BUT NOT the same flight time

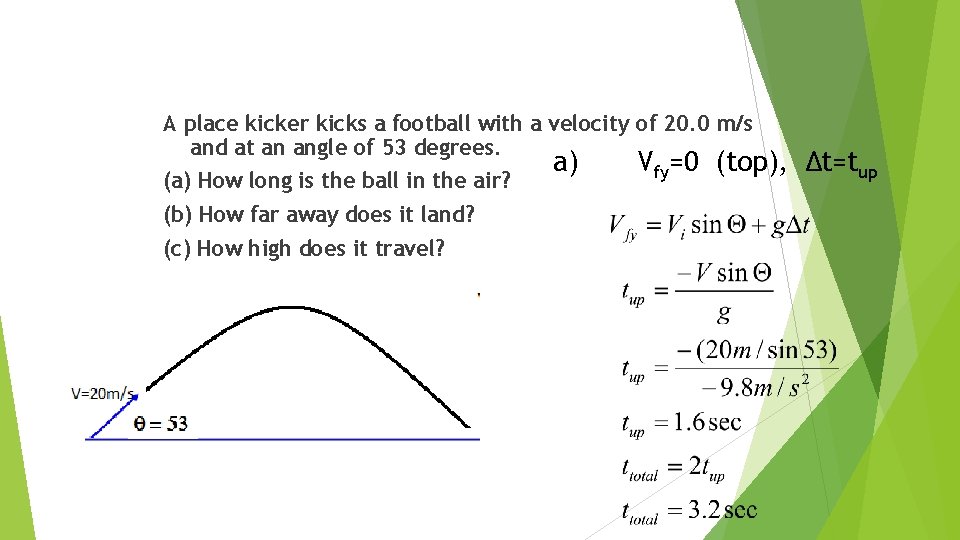
A place kicker kicks a football with a velocity of 20. 0 m/s and at an angle of 53 degrees. (a) How long is the ball in the air? (b) How far away does it land? (c) How high does it travel? a) Vfy=0 (top), ∆t=tup

b) ∆dt =? , need ttotal c) ∆ymax = ? Use Vfy = 0 m/s and tup