Projectile Motion Examples Example 4 3 The Long

Projectile Motion Examples

Example 4. 3: The Long Jump Problem: A long-jumper (Fig. 4. 12) leaves the ground at an angle θi = 20° above the horizontal at a speed of vi = 8. 0 m/s. a) How far does he jump in the horizontal direction? (Assume his motion is equivalent to that of a particle. ) b) What is the maximum height reached?

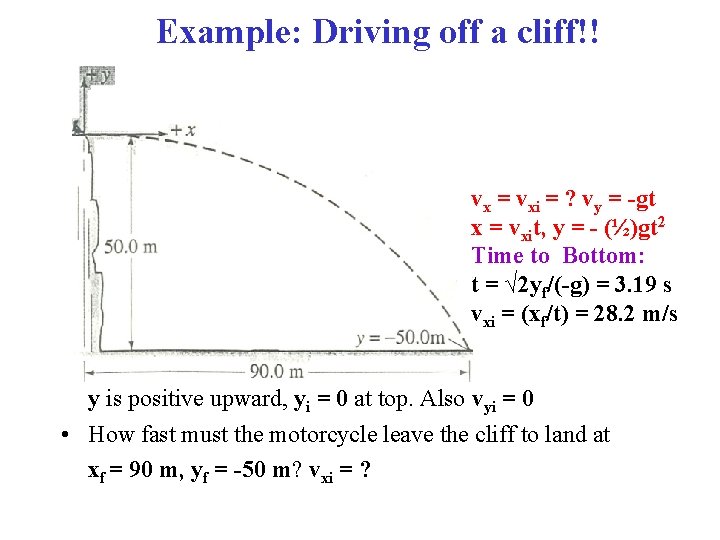
Example: Driving off a cliff!! vx = vxi = ? vy = -gt x = vxit, y = - (½)gt 2 Time to Bottom: t = √ 2 yf/(-g) = 3. 19 s vxi = (xf/t) = 28. 2 m/s y is positive upward, yi = 0 at top. Also vyi = 0 • How fast must the motorcycle leave the cliff to land at xf = 90 m, yf = -50 m? vxi = ?

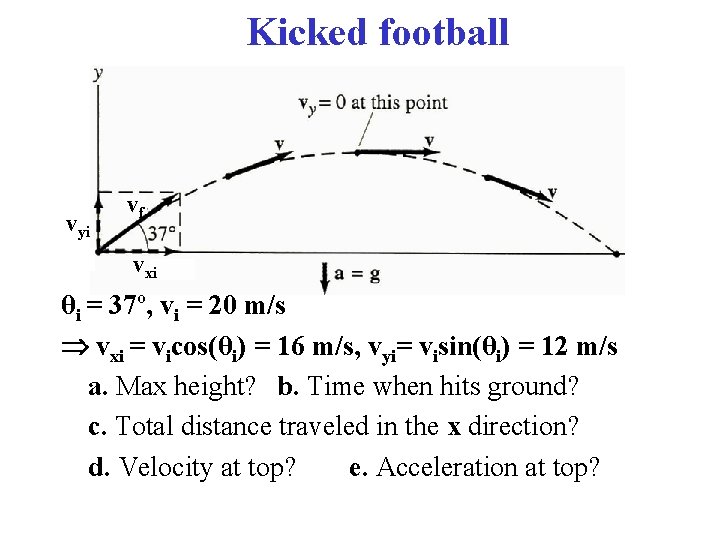
Kicked football vyi vf vxi θi = 37º, vi = 20 m/s vxi = vicos(θi) = 16 m/s, vyi= visin(θi) = 12 m/s a. Max height? b. Time when hits ground? c. Total distance traveled in the x direction? d. Velocity at top? e. Acceleration at top?

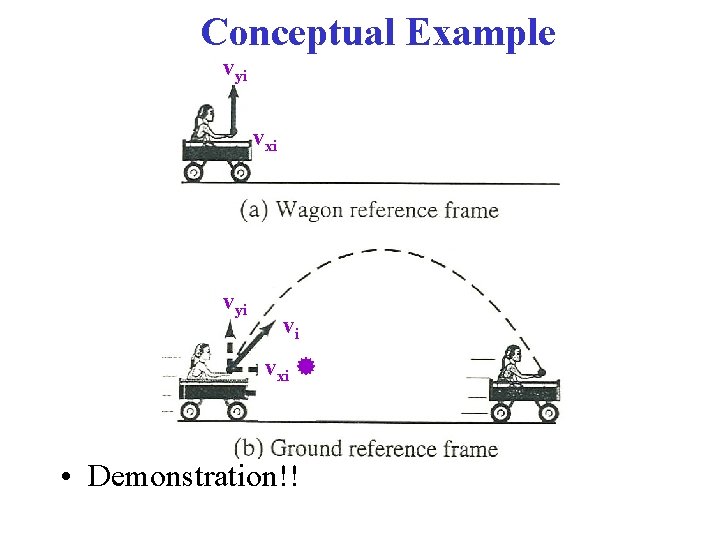
Conceptual Example vyi vxi vyi vi vxi • Demonstration!!

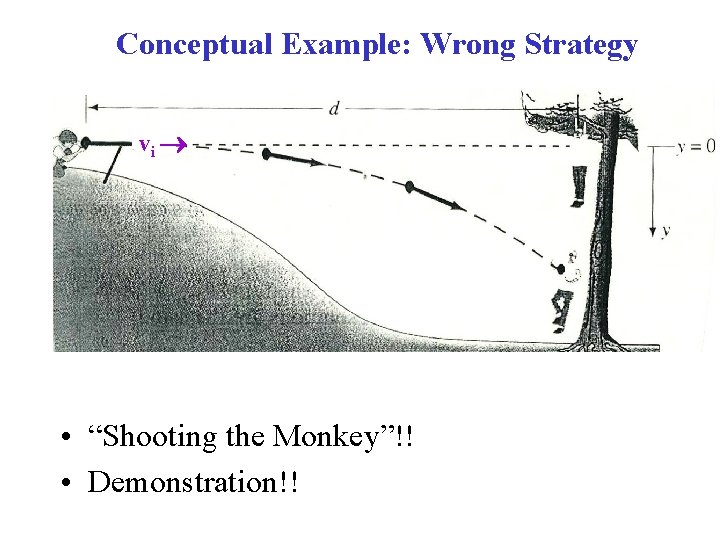
Conceptual Example: Wrong Strategy vi • “Shooting the Monkey”!! • Demonstration!!

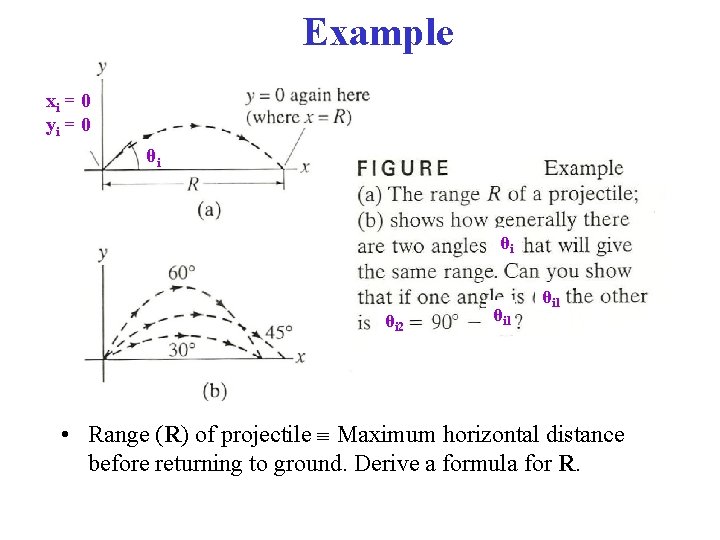
Example xi = 0 yi = 0 θi θi θi 2 θi 1 • Range (R) of projectile Maximum horizontal distance before returning to ground. Derive a formula for R.

• Range R the x where y = 0! • Use vxf = vxi , xf = vxi t , vyf = vyi - gt yf = vyi t – (½)g t 2, (vyf) 2 = (vyi)2 - 2 gyf • First, find the time t when y = 0 0 = vyi t - (½)g t 2 t = 0 (of course!) and t = (2 vyi)/g • Put this t in the x formula: xf = vxi (2 vyi)/g R R = 2(vxivyi)/g, vxi= vicos(θi), vyi= visin(θi) R = (vi)2 [2 sin(θi)cos(θi)]/g R = (vi)2 sin(2θi)/g (by a trig identity)

Example 4. 5: That’s Quite an Arm! Problem: A stone is thrown from the top of a building at an angle θi = 26° to the horizontal and with an initial speed vi = 17. 9 m/s, as in Fig. 4. 14. The height of the building is 45. 0 m. a) How long is the stone "in flight"? b) What is the speed of the stone just before it strikes the ground?

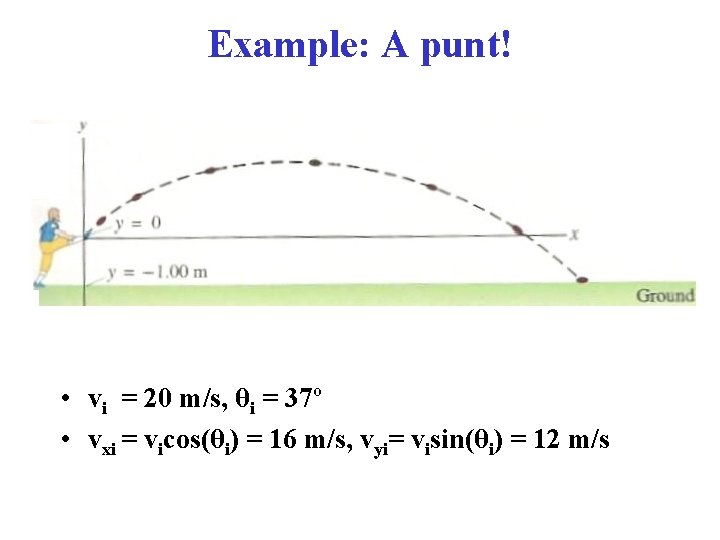
Example: A punt! • vi = 20 m/s, θi = 37º • vxi = vicos(θi) = 16 m/s, vyi= visin(θi) = 12 m/s

Proof that projectile path is a parabola • xf = vxi t , yf = vyi t – (½)g t 2 Note: The same time t enters both equations! Eliminate t to get y as a function of x. Solve x equation for t: t = xf/vxi Get: yf = vyi (xf/vxi) – (½)g (xf/vxi)2 Or: yf = (vyi /vxi)xf - [(½)g/(vxi)2](xf)2 Of the form yf = Axf – B(xf)2 A parabola in the x-y plane!!

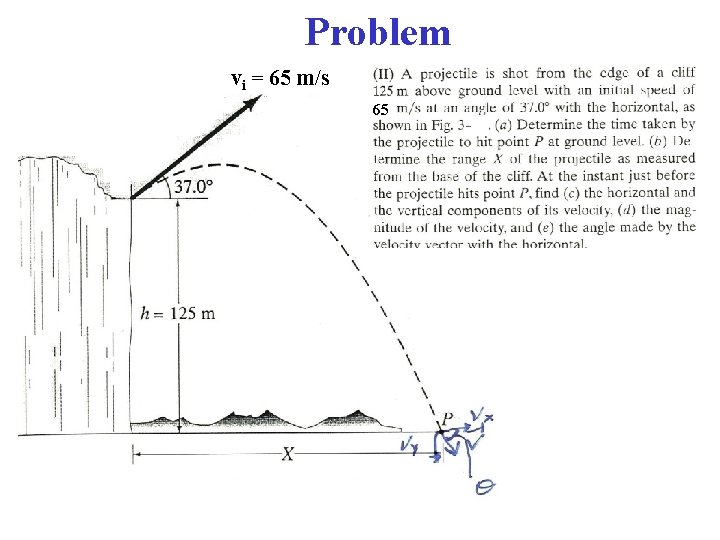
Problem vi = 65 m/s 65

Example 4. 6: The Stranded Explorers Problem: An Alaskan rescue plane drops a package of emergency rations to a stranded party of explorers, as shown in the picture. If the plane is traveling horizontally at vi = 42. 0 m/s at a height h = 106 m above the ground, where does the package strike the ground relative to the point at which it is released? vi = 65 m/s h