Projectile Motion Example Problem 3 In the previous

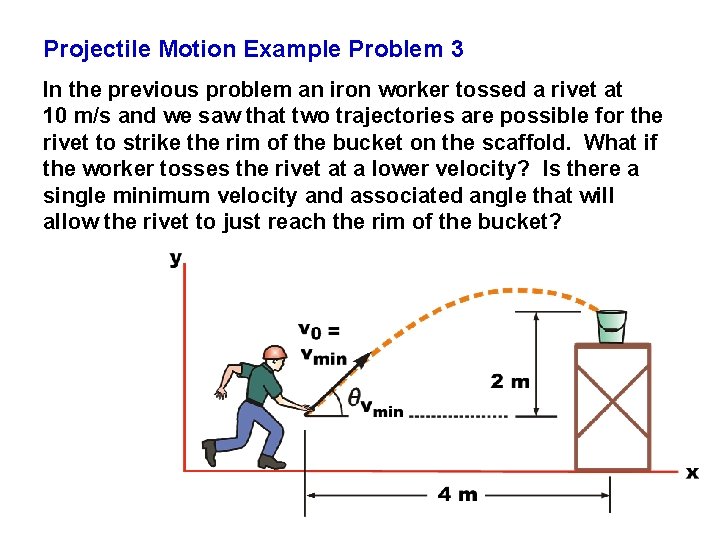
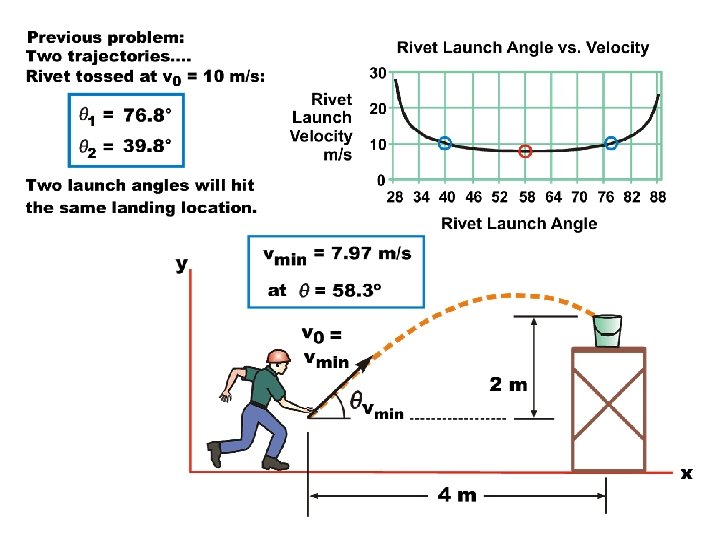
Projectile Motion Example Problem 3 In the previous problem an iron worker tossed a rivet at 10 m/s and we saw that two trajectories are possible for the rivet to strike the rim of the bucket on the scaffold. What if the worker tosses the rivet at a lower velocity? Is there a single minimum velocity and associated angle that will allow the rivet to just reach the rim of the bucket?

Where are we going? We’re seeking an equation relating v 0 and q.

This v = f(q) function defines the set (an infinite number) of all combinations of v 0 and q for trajectories that will hit the target.

Now that we have the v = f(q) function, take the derivative with respect to q, set it equal to zero, and find the minimum v and the associated angle.

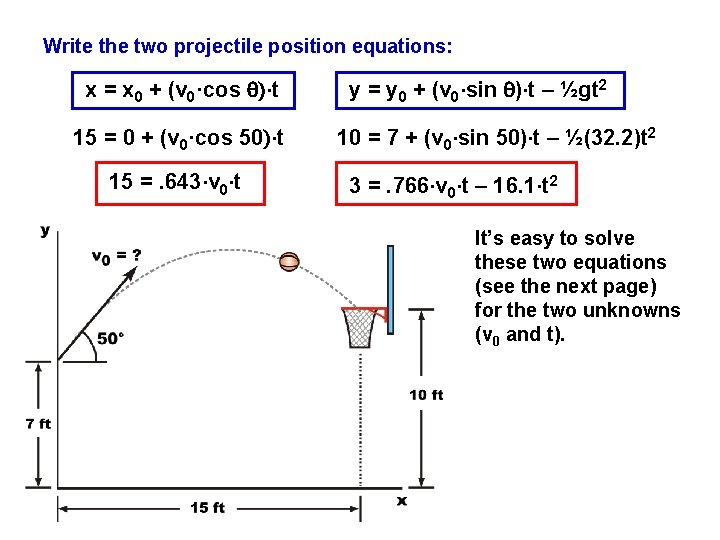
Write the two projectile position equations: x = x 0 + (v 0·cos q)·t 15 = 0 + (v 0·cos 50)·t 15 =. 643·v 0·t y = y 0 + (v 0·sin q)·t – ½gt 2 10 = 7 + (v 0·sin 50)·t – ½(32. 2)t 2 3 =. 766·v 0·t – 16. 1·t 2 It’s easy to solve these two equations (see the next page) for the two unknowns (v 0 and t).

There are several ways to solve for v 0 and t, but I prefer to substitute the v 0 t product from the first equation into the second: 15 =. 643·v 0·t 3 =. 766·v 0·t – 16. 1·t 2 23. 34 = v 0·t 3 =. 766·(23. 34)– 16. 1·t 2 = 17. 88 – 3 = 14. 88 t = 0. 961 sec 23. 34 = v 0·t v 0 = 24. 3 fps

Now find the height of the apex of the trajectory: v 0 = 24. 3 fps v 0 y = 24. 3(sin 50) = 18. 6 fps Easiest equation to use for this: vy 2 = v 0 y 2 – 2 g(y – y 0) 0 = (18. 6)2 – 2(32. 2)(y - 7) y = hmax = 12. 38 ft This is a low trajectory. A good free throw should have a larger launch and a higher arc.

Finally, find the speed angle of the ball as it passes through the rim: