Projectile Motion Example Problem 1 A player shoots

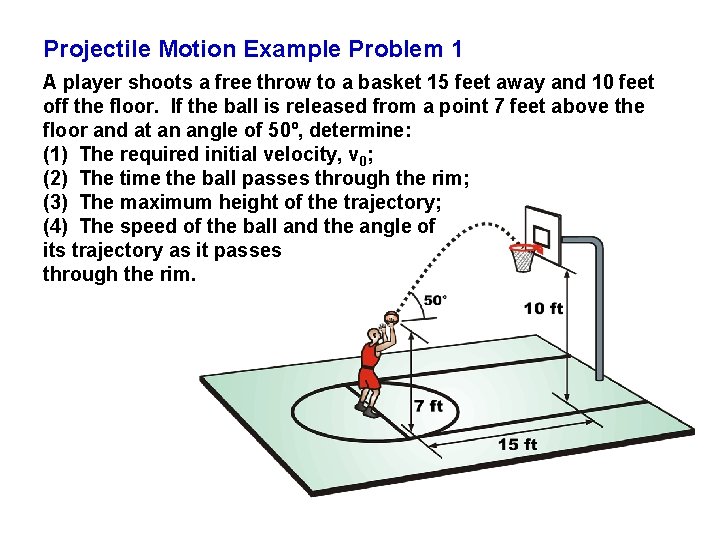
Projectile Motion Example Problem 1 A player shoots a free throw to a basket 15 feet away and 10 feet off the floor. If the ball is released from a point 7 feet above the floor and at an angle of 50º, determine: (1) The required initial velocity, v 0; (2) The time the ball passes through the rim; (3) The maximum height of the trajectory; (4) The speed of the ball and the angle of its trajectory as it passes through the rim.

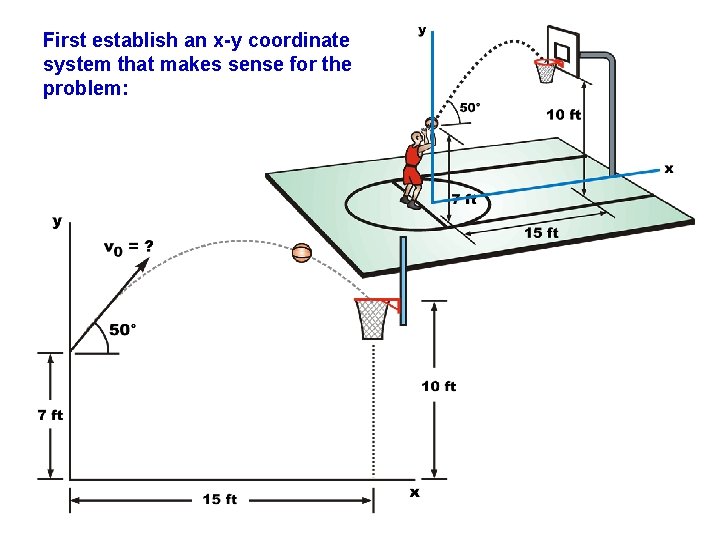
First establish an x-y coordinate system that makes sense for the problem:

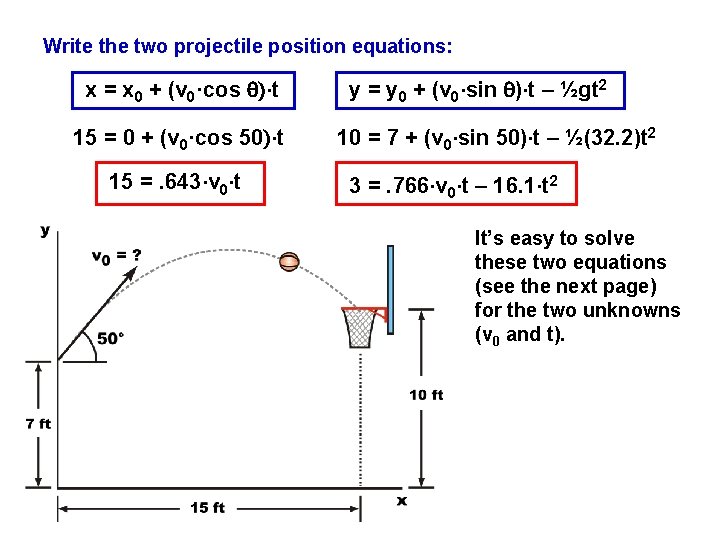
Write the two projectile position equations: x = x 0 + (v 0·cos q)·t 15 = 0 + (v 0·cos 50)·t 15 =. 643·v 0·t y = y 0 + (v 0·sin q)·t – ½gt 2 10 = 7 + (v 0·sin 50)·t – ½(32. 2)t 2 3 =. 766·v 0·t – 16. 1·t 2 It’s easy to solve these two equations (see the next page) for the two unknowns (v 0 and t).

There are several ways to solve for v 0 and t, but I prefer to substitute the v 0 t product from the first equation into the second: 15 =. 643·v 0·t 3 =. 766·v 0·t – 16. 1·t 2 23. 34 = v 0·t 3 =. 766·(23. 34)– 16. 1·t 2 = 17. 88 – 3 = 14. 88 t = 0. 961 sec 23. 34 = v 0·t v 0 = 24. 3 fps

Now find the height of the apex of the trajectory: v 0 = 24. 3 fps v 0 y = 24. 3(sin 50) = 18. 6 fps Easiest equation to use for this: vy 2 = v 0 y 2 – 2 g(y – y 0) 0 = (18. 6)2 – 2(32. 2)(y - 7) y = hmax = 12. 38 ft This is a low trajectory. A good free throw should have a larger launch angle and a higher arc.

Finally, find the speed angle of the ball as it passes through the rim: