PROJECTILE MOTION Chapter 3 sections 3 1 3

PROJECTILE MOTION Chapter 3, sections 3. 1 -3. 3, 3. 5

EXAMPLES OF PROJECTILE MOTION

PROJECTILE MOTION vx v 1 vx: Horizontal Velocity. Once in air, vx does not change since there is no force pushing or pulling horizontally. v 2 vy: Vertical Velocity. Once in air, vy changes because of the force of gravity. The projectile accelerates at the rate of 9. 8 m/s 2 downward. v 3 PM simulation

PROJECTILE MOTION • A projectile is an object shot through the air upon which the only force acting is gravity (neglecting air resistance). • The trajectory (path through space) or a projectile is parabolic.

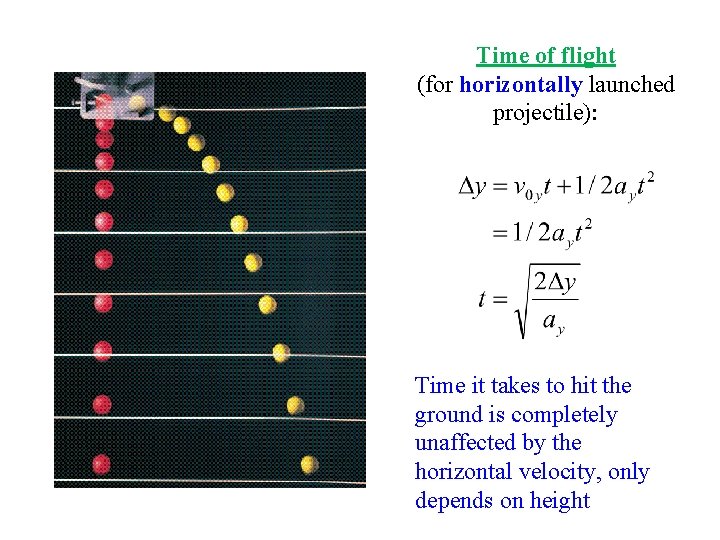
Time of flight (for horizontally launched projectile): Time it takes to hit the ground is completely unaffected by the horizontal velocity, only depends on height

The horizontal part of a projectile motion problem is a constant velocity problem. • • The vertical part of a projectile motion problem is a free fall problem. • Horizontal and vertical parts of the motion are independent • To solve a projectile motion problem, break up the motion into x and y components.

Kinematics Equations for uniformly accelerated motion Horizontal (ax=0) Vertical (FREE FALL)

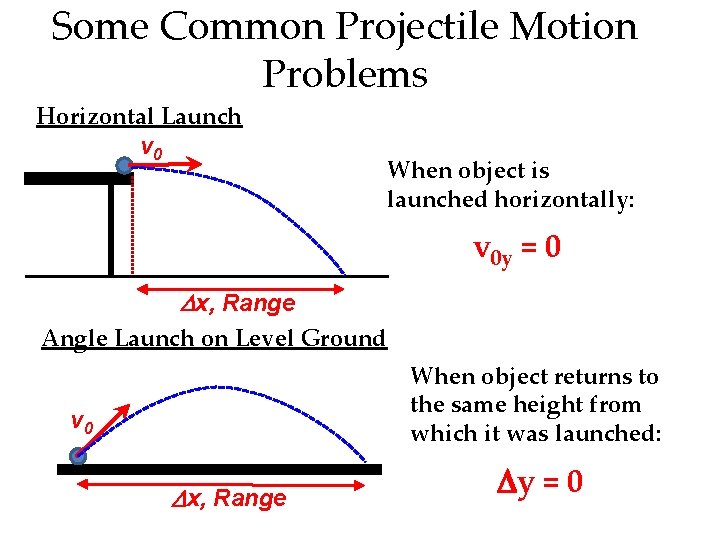
Some Common Projectile Motion Problems Horizontal Launch v 0 When object is launched horizontally: v 0 y = 0 Dx, Range Angle Launch on Level Ground When object returns to the same height from which it was launched: v 0 Dx, Range Dy = 0

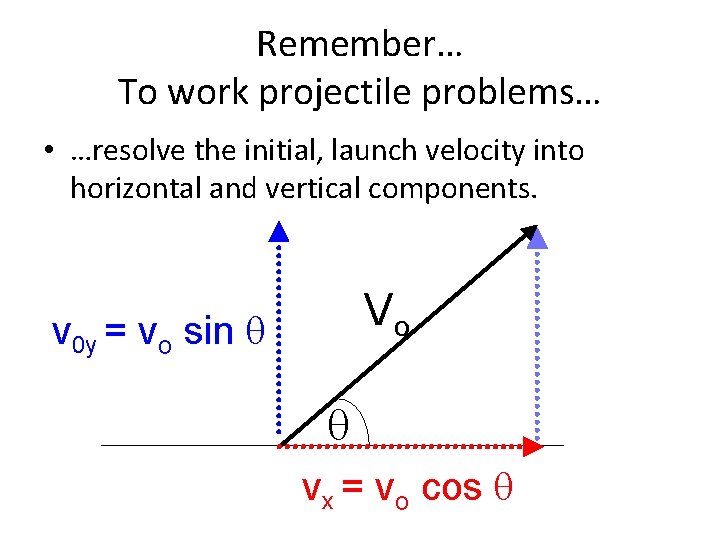
Remember… To work projectile problems… • …resolve the initial, launch velocity into horizontal and vertical components. Vo v 0 y = vo sin vx = vo cos

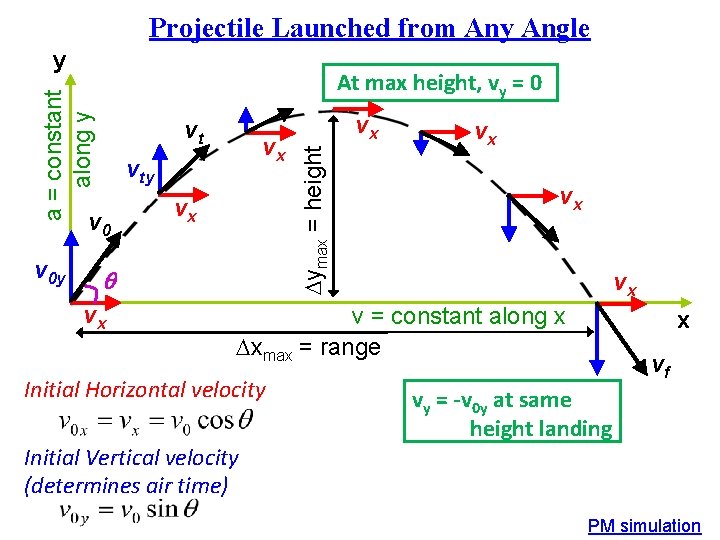
Projectile Launched from Any Angle y vt vty v 0 y vx vx q vx vx Dymax = height a = constant along y At max height, vy = 0 vx vx vx v = constant along x Dxmax = range Initial Horizontal velocity Initial Vertical velocity (determines air time) x vf vy = -v 0 y at same height landing PM simulation

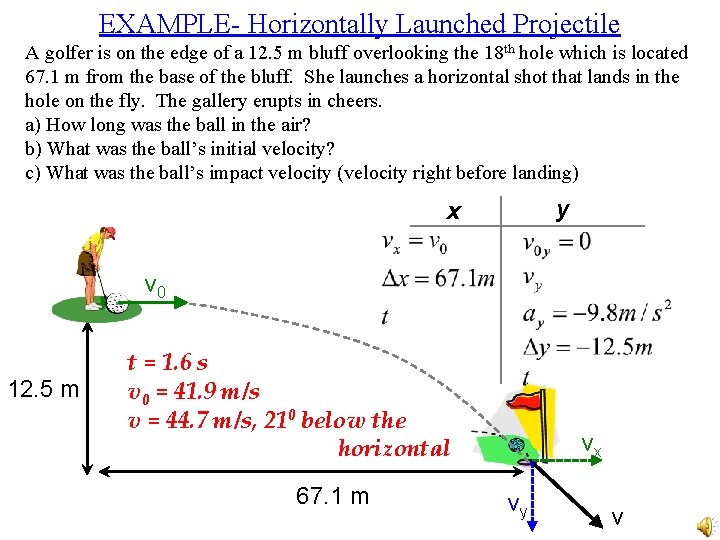
EXAMPLE- Horizontally Launched Projectile A golfer is on the edge of a 12. 5 m bluff overlooking the 18 th hole which is located 67. 1 m from the base of the bluff. She launches a horizontal shot that lands in the hole on the fly. The gallery erupts in cheers. a) How long was the ball in the air? b) What was the ball’s initial velocity? c) What was the ball’s impact velocity (velocity right before landing) y x v 0 12. 5 m t = 1. 6 s v 0 = 41. 9 m/s v = 44. 7 m/s, 210 below the horizontal 67. 1 m vx vy v

EXAMPLE –Projectile Launched over Level Ground In the circus, a clown is launched from a cannon at 40 m/s, 60 o from the horizontal. Where should the other clowns hold the net so that the projectile clown lands unharmed (at the same level)? v 0 = v 0 y vx 40 m /s t = 7. 07 s Dx = 141 m

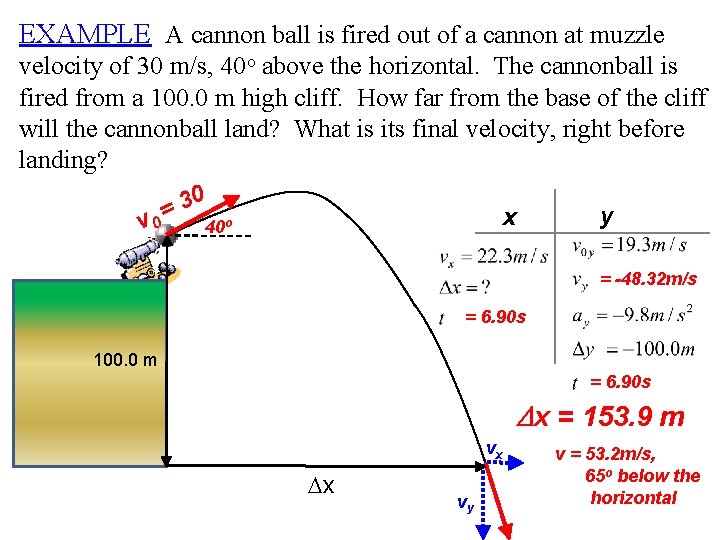
EXAMPLE A cannon ball is fired out of a cannon at muzzle velocity of 30 m/s, 40 o above the horizontal. The cannonball is fired from a 100. 0 m high cliff. How far from the base of the cliff will the cannonball land? What is its final velocity, right before landing? v 0 0 3 = y x 40 o = -48. 32 m/s = 6. 90 s 100. 0 mm = 6. 90 s Dx = 153. 9 m vx Dx vy v = 53. 2 m/s, 65 o below the horizontal

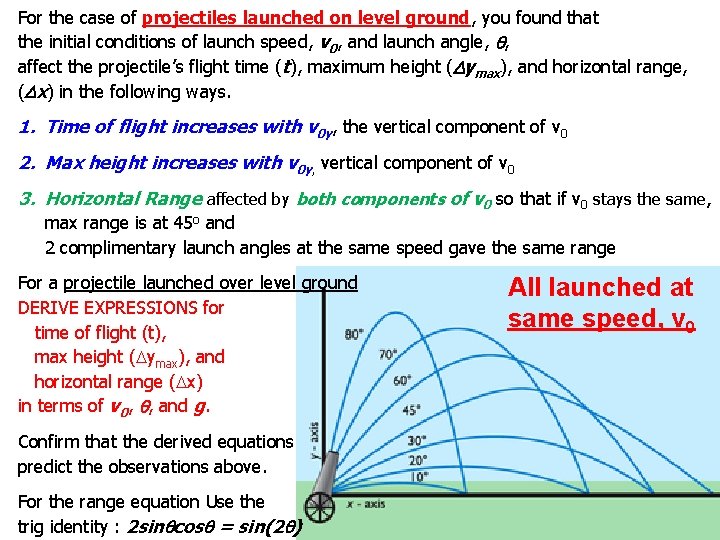
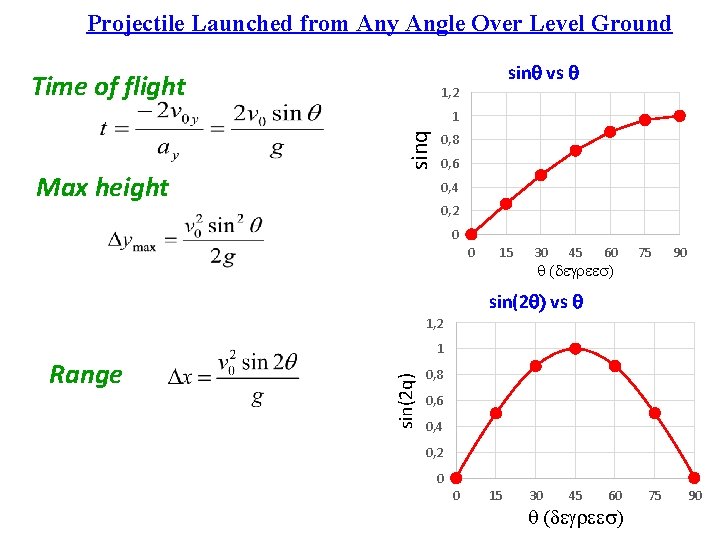
For the case of projectiles launched on level ground, you found that the initial conditions of launch speed, v 0, and launch angle, q, affect the projectile’s flight time (t), maximum height (Dymax), and horizontal range, (Dx) in the following ways. 1. Time of flight increases with v 0 y, the vertical component of v 0 2. Max height increases with v 0 y, vertical component of v 0 3. Horizontal Range affected by both components of v 0 so that if v 0 stays the same, max range is at 45 o and 2 complimentary launch angles at the same speed gave the same range For a projectile launched over level ground DERIVE EXPRESSIONS for time of flight (t), max height (Dymax), and horizontal range (Dx) in terms of v 0, q, and g. Confirm that the derived equations predict the observations above. For the range equation Use the trig identity : 2 sinqcosq = sin(2 q) All launched at same speed, v 0

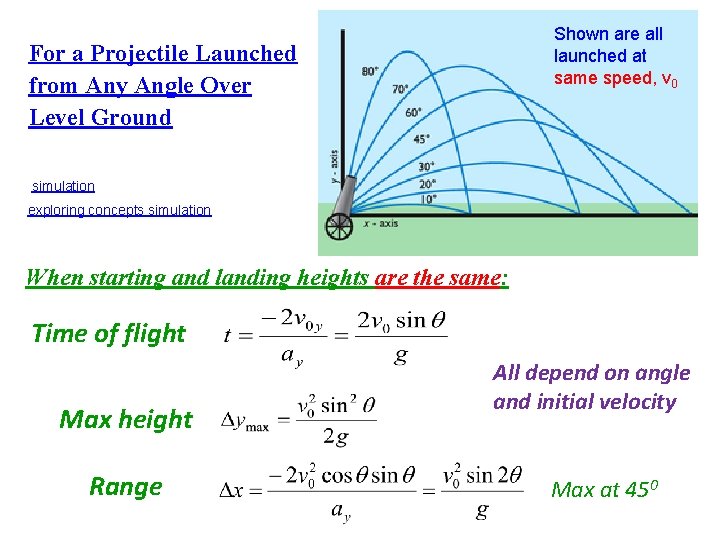
Shown are all launched at same speed, v 0 For a Projectile Launched from Any Angle Over Level Ground simulation exploring concepts simulation When starting and landing heights are the same: Time of flight Max height Range All depend on angle and initial velocity Max at 450

Projectile Launched from Any Angle Over Level Ground Time of flight sinq vs q 1, 2 Max height sinq 1 0, 8 0, 6 0, 4 0, 2 0 0 15 30 45 60 (degrees) 75 90 sin(2 q) vs q 1, 2 sin(2 q) Range 1 0, 8 0, 6 0, 4 0, 2 0 0 15 30 45 60 (degrees) 75 90

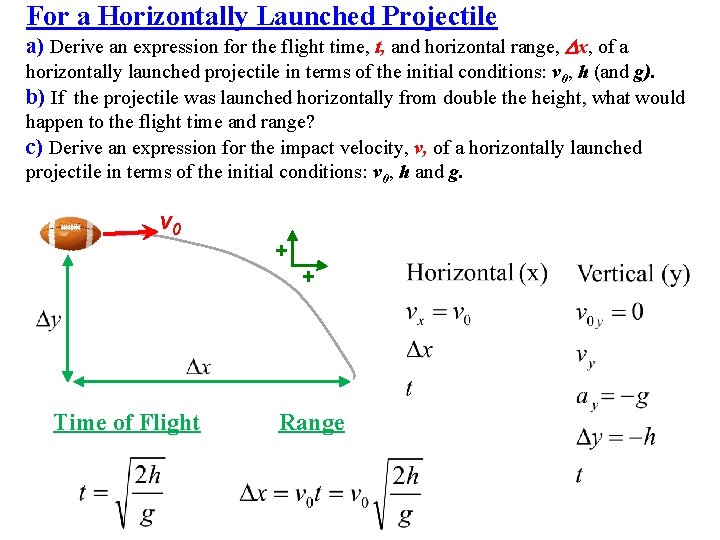
For a Horizontally Launched Projectile a) Derive an expression for the flight time, t, and horizontal range, Dx, of a horizontally launched projectile in terms of the initial conditions: v 0, h (and g). b) If the projectile was launched horizontally from double the height, what would happen to the flight time and range? c) Derive an expression for the impact velocity, v, of a horizontally launched projectile in terms of the initial conditions: v 0, h and g. v 0 + + Time of Flight Range

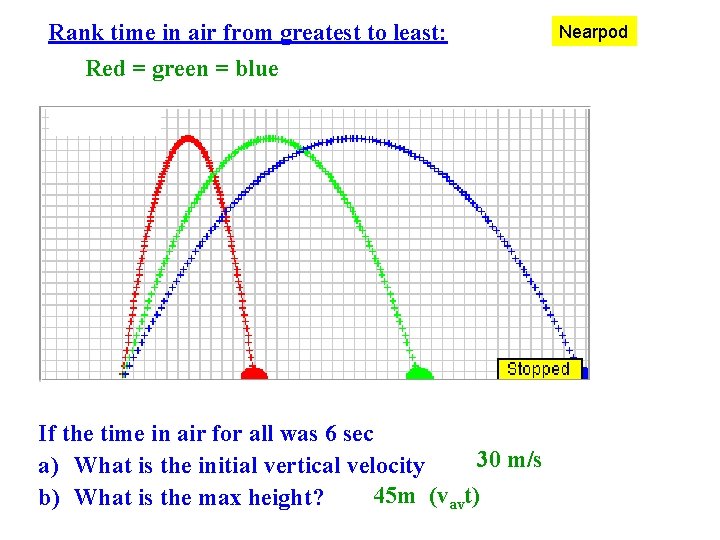
Rank time in air from greatest to least: Red = green = blue If the time in air for all was 6 sec 30 m/s a) What is the initial vertical velocity 45 m (vavt) b) What is the max height? Nearpod

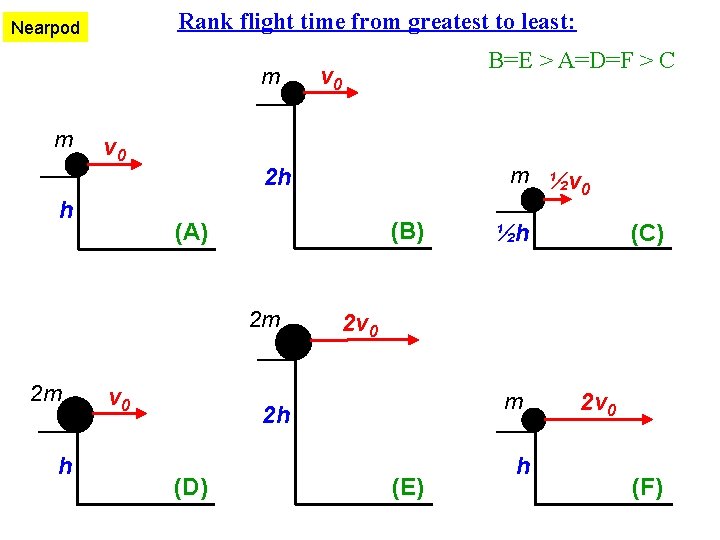
Rank flight time from greatest to least: Nearpod m m v 0 h h v 0 m ½v 0 2 h (B) (A) 2 m 2 m B=E > A=D=F > C v 0 2 v 0 m 2 h (D) (C) ½h (E) h 2 v 0 (F)

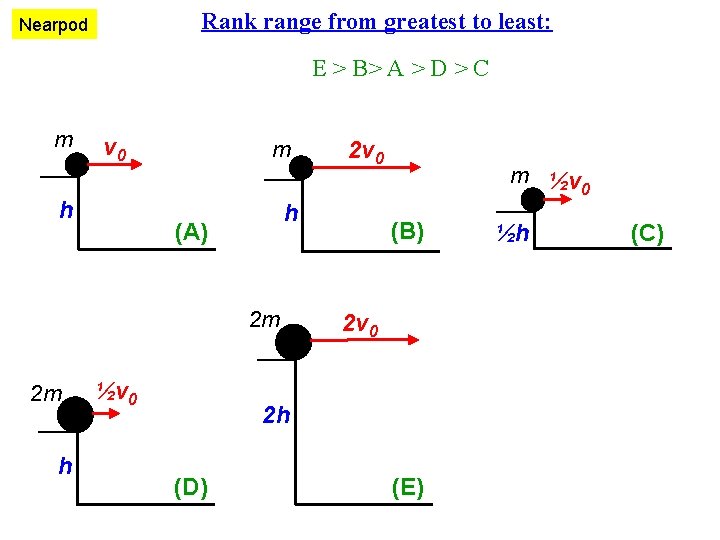
Rank range from greatest to least: Nearpod E > B> A > D > C m v 0 h m h (A) 2 m 2 m h ½v 0 2 v 0 m ½v 0 (B) 2 v 0 2 h (D) (E) ½h (C)

Nearpod EXAMPLE- Projectile over Level ground A player kicks a football from ground level with an initial velocity of 27 m/s at an angle of 30 o above the horizontal. The ball lands at the same height. Neglect air resistance. If the player then kicks the ball with the same speed but at a 60 o angle, How do the following quantities change? s v 0 m/ 7 =2 =2 7 m /s Flight time increases, decreases, stays the same, cant be determined Maximum height increases, decreases, stays the same, cant be determined Horizontal Range increases, decreases, stays the same, cant be determined Impact velocity increases, decreases, stays the same, cant be determined v 0 a) b) c) d)

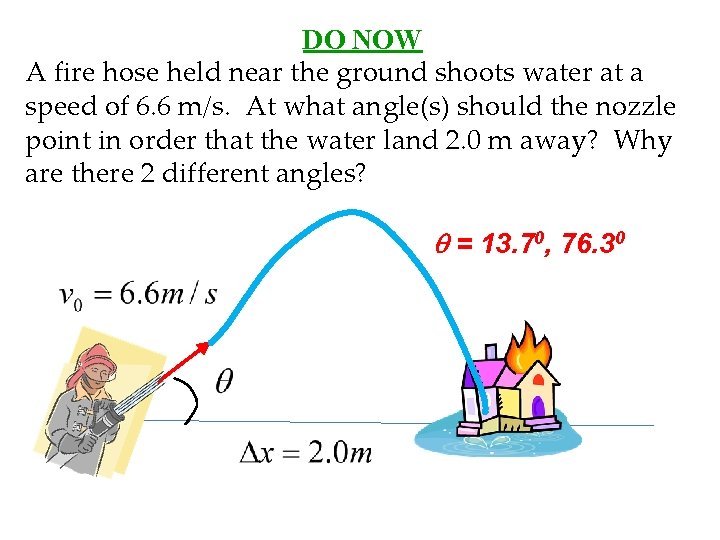
DO NOW A fire hose held near the ground shoots water at a speed of 6. 6 m/s. At what angle(s) should the nozzle point in order that the water land 2. 0 m away? Why are there 2 different angles? q = 13. 70, 76. 30

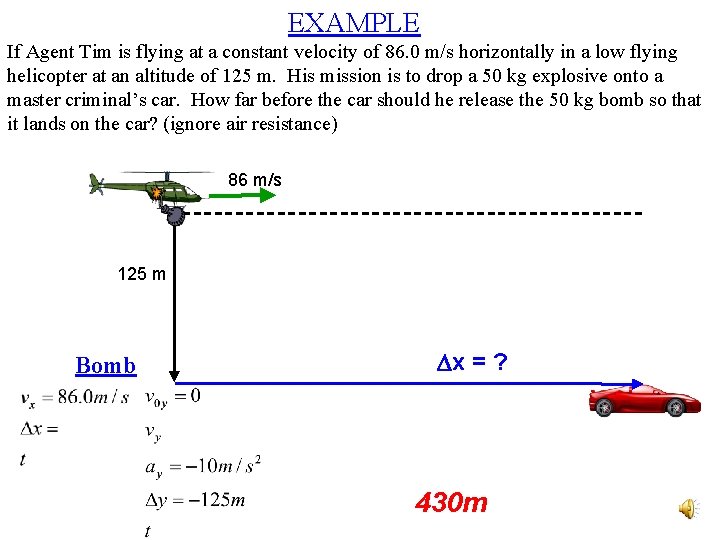
EXAMPLE If Agent Tim is flying at a constant velocity of 86. 0 m/s horizontally in a low flying helicopter at an altitude of 125 m. His mission is to drop a 50 kg explosive onto a master criminal’s car. How far before the car should he release the 50 kg bomb so that it lands on the car? (ignore air resistance) 86 m/s 125 m Bomb Dx = ? 430 m

Cargo Drop

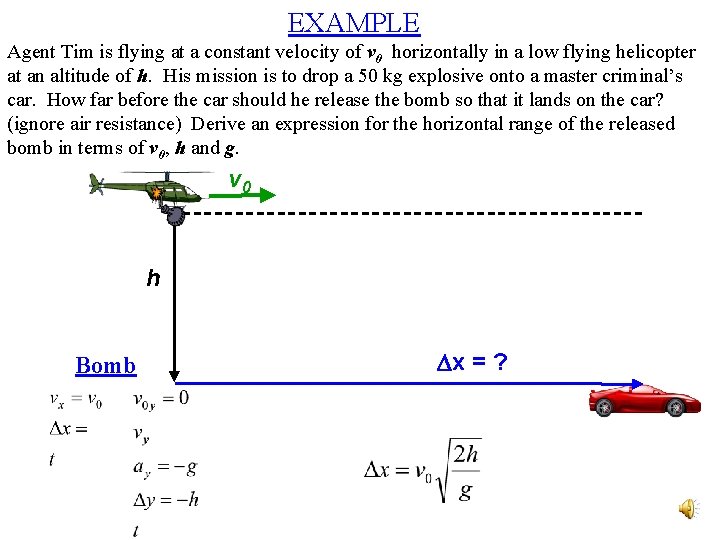
EXAMPLE Agent Tim is flying at a constant velocity of v 0 horizontally in a low flying helicopter at an altitude of h. His mission is to drop a 50 kg explosive onto a master criminal’s car. How far before the car should he release the bomb so that it lands on the car? (ignore air resistance) Derive an expression for the horizontal range of the released bomb in terms of v 0, h and g. v 0 h Bomb Dx = ?

EXAMPLE A professional soccer player is 25. 8 m from the goal and kicks a hard shot at ground level. The ball hits the cross bar on its way down, 2. 44 m above the ground, 1. 98 s after being kicked. What was the initial velocity of the ball (find the x- and y- components)? x y vx = 13. 0 m/s v 0 y = 11. 13 m/s v 0 = 17. 1 m/s, 40 o 2. 44 m 25. 8 m

Great simulations of Projectile Motion Any type of projectile (by Mr Walsh) http: //tube. geogebra. org/student/m 167259 Projectile over level ground https: //phet. colorado. edu/sims/projectilemotion/projectile-motion_en. html Exploring Concepts: Several projectiles with same range OR Same max height OR Same initial speed http: //tube. geogebra. org/student/m 224687

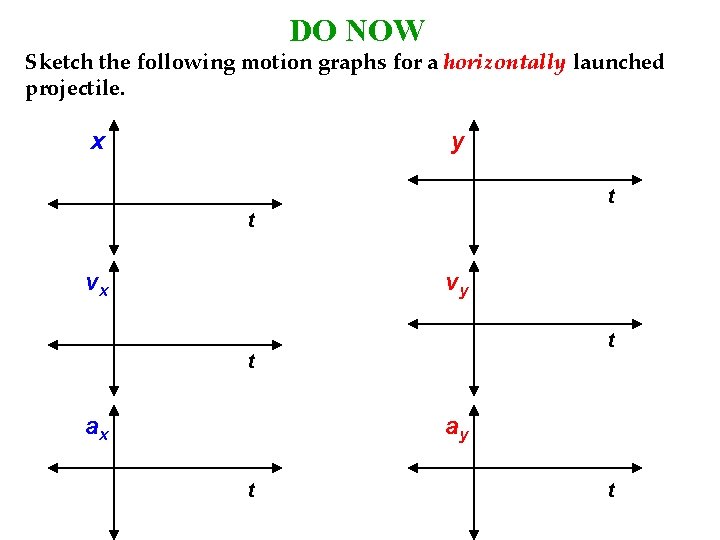
DO NOW Sketch the following motion graphs for a horizontally launched projectile. x y t t vx vy t t ax ay t t

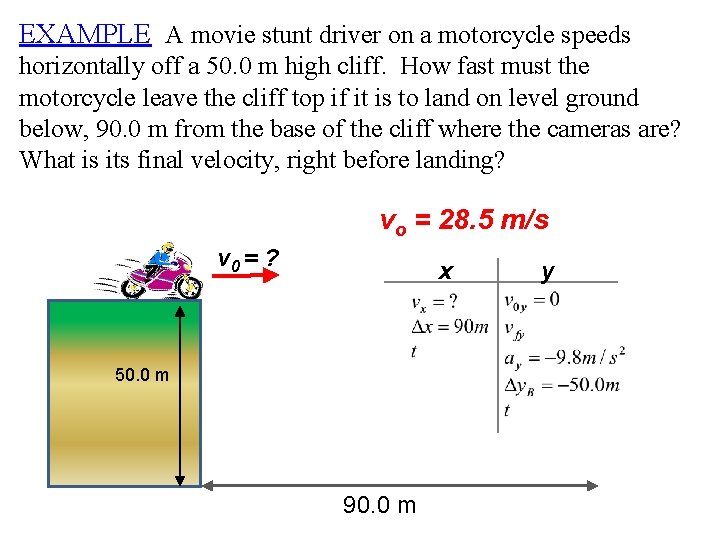
EXAMPLE A movie stunt driver on a motorcycle speeds horizontally off a 50. 0 m high cliff. How fast must the motorcycle leave the cliff top if it is to land on level ground below, 90. 0 m from the base of the cliff where the cameras are? What is its final velocity, right before landing? vo = 28. 5 m/s v 0 = ? x 50. 0 m 90. 0 m y

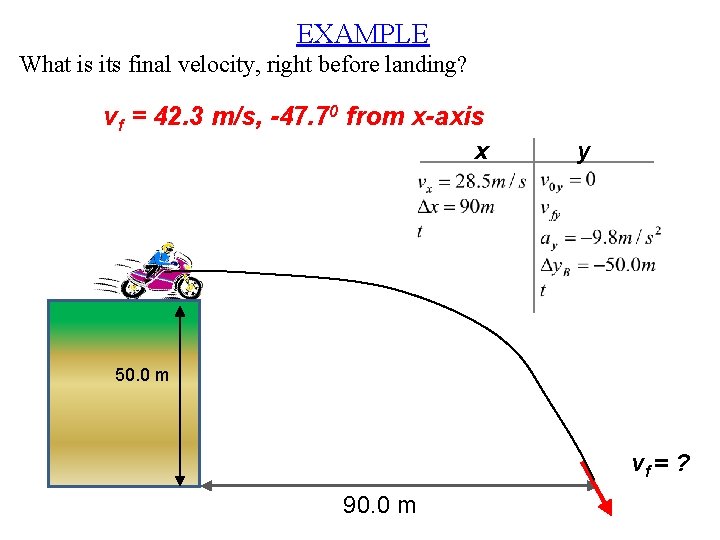
EXAMPLE What is its final velocity, right before landing? vf = 42. 3 m/s, -47. 70 from x-axis x y 50. 0 m vf = ? 90. 0 m