Projectile Motion Basic Rules 2 D motion X

Projectile Motion • • Basic Rules 2 -D motion – X and Y equations Example 1 – ball dropped from cliff Example 2 – ball thrown horz. from cliff Example 3 -4 Symmetric Football Asymmetric Football

Projectile Motion • Break position, velocity, and acceleration into x and y components, solve as separate x and y problems • 2 Independent constant-accelerations problem! – ay = - 9. 8 m/s 2, ax = 0 m/s 2 – ax = -9. 8 m/s 2 proven method of losing 10 pts! – Question: How often does book accelerate toward wall? • vx = v cosӨ , vy = v sinӨ • x and y ONLY connect during obvious event (hitting ground, etc) • Reassemble x and y as last step if requested!

Projectile Motion • X and Y independent!

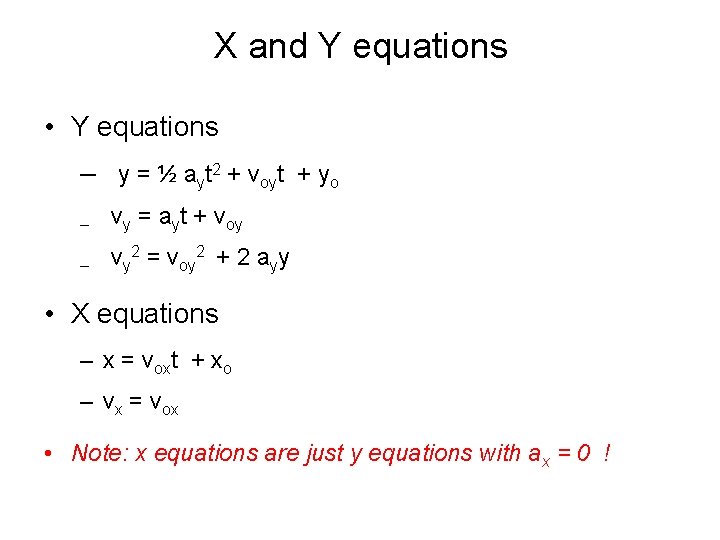
X and Y equations • Y equations – y = ½ ayt 2 + voyt + yo – vy = ayt + voy 2 2 – vy = voy + 2 ayy • X equations – x = voxt + xo – vx = vox • Note: x equations are just y equations with ax = 0 !

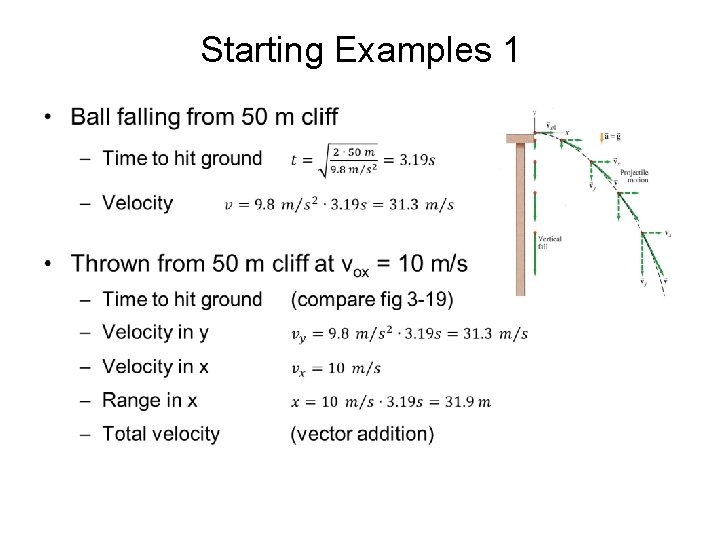
Starting Examples 1 •

Example 2 – Stunt Driver • Example 3 -5 – Ball thrown from 50 m cliff, travels 90 m – Time in air determined by y – Range in x determined by vox and time in air – Uniquely determines vox

Example 4 - Football • Field Goal

Example 4 - Symmetric Football • Football kicked at 20 m/s and θ = 37 – V 0 x = 20 cos θ, V 0 y = 20 sin θ – ax = 0 m/s 2 , ay = -9. 8 m/s 2 – Time to maximum height – Maximum height – Velocity at maximum height – Range to maximum height – Time to hit ground – Distance at hit ground – Velocity at hit ground

Example 5 - Asymmetric Football • Football kicked at 20 m/s @ 37° - 1 m high – Time to hit ground – Distance to hit ground – Eliminate non-physical time

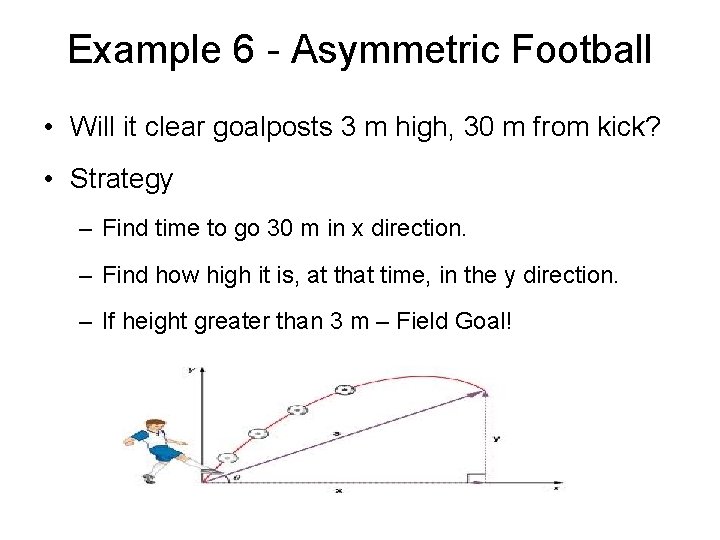
Example 6 - Asymmetric Football • Will it clear goalposts 3 m high, 30 m from kick? • Strategy – Find time to go 30 m in x direction. – Find how high it is, at that time, in the y direction. – If height greater than 3 m – Field Goal!

Other examples • Problem 18 • Problem 21 • Problem 31

Example 3 – Syringe Fountain • X and Y Equations – y = ½ ayt 2 + voyt (constant acceleration – x = voxt (constant velocity) • Combine and eliminate t – y = ½ (ay/vox 2)x 2 + (voy/vox)x – Equation of parabola – Public Fountains • Syringe, Bank fountains

Range Equation • X and Y equations – y = ½ gt 2 + voyt + yo x = voxt + xo • Find time when y = 0 – 0 = ½ gt 2 + voyt – t = 0, t = 2 voy / g • Then find x – x = voxt = 2 voxvoy / g – x = 2 vo 2 sinΘ cosΘ / g – x = vo 2 sin 2Θ / g • Θ = 0 (min), Θ = 90 (min), Θ =45 (max) • Trade-off between x and y motion • Only works for symmetric

Other examples • Problem 23