Projectile Motion An object solely under the inf

Projectile Motion An object solely under the inf. Bluence of gravity that has a combination of constant horizontal speed and accelerated vertical speed, so that it moves along a parabola shaped trajectory path Ex: Not:

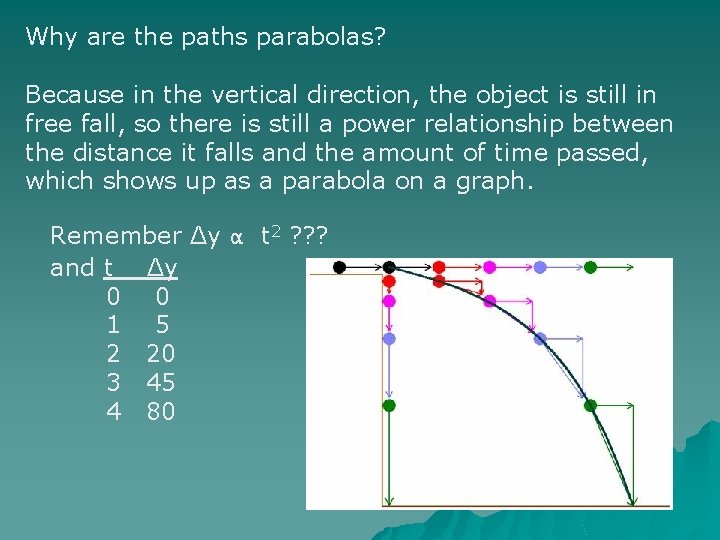
Why are the paths parabolas? Because in the vertical direction, the object is still in free fall, so there is still a power relationship between the distance it falls and the amount of time passed, which shows up as a parabola on a graph. Remember Δy α t 2 ? ? ? and t Δy 0 0 1 5 2 20 3 45 4 80

The most important thing to remember about projectile motion is that the horizontal motion doesn’t affect (is completely independent from) the vertical motion, and vice versa. So then which ball wins on the PM demonstrator – dropped or launched? NEITHER! The fact that the launched one has a horizontal velocity does not affect the rate at which it falls. It falls at the same rate as the one that is simply dropped, so they reach the floor at the same time. Another way to think of it is that even though the launched ball travels a further (horizontal) distance, it has some extra (horizontal) speed, to get it there, but vertically, both balls are identical. go back to previous diagram to see…

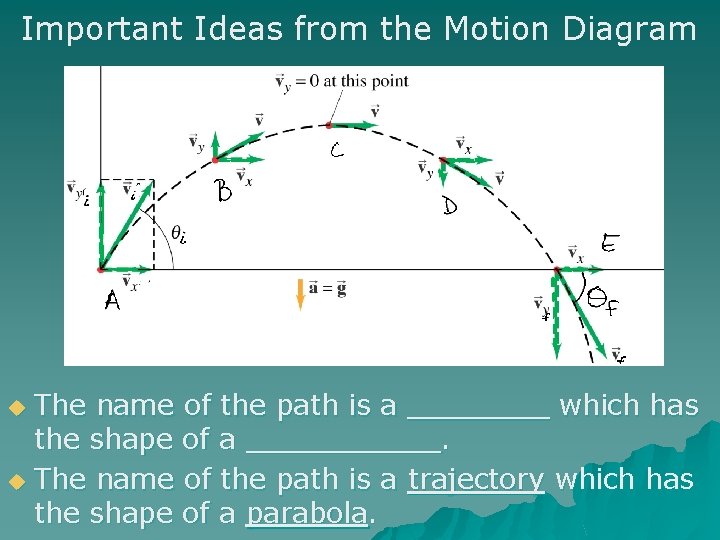
Important Ideas from the Motion Diagram The name of the path is a ____ which has the shape of a ______. u The name of the path is a trajectory which has the shape of a parabola. u

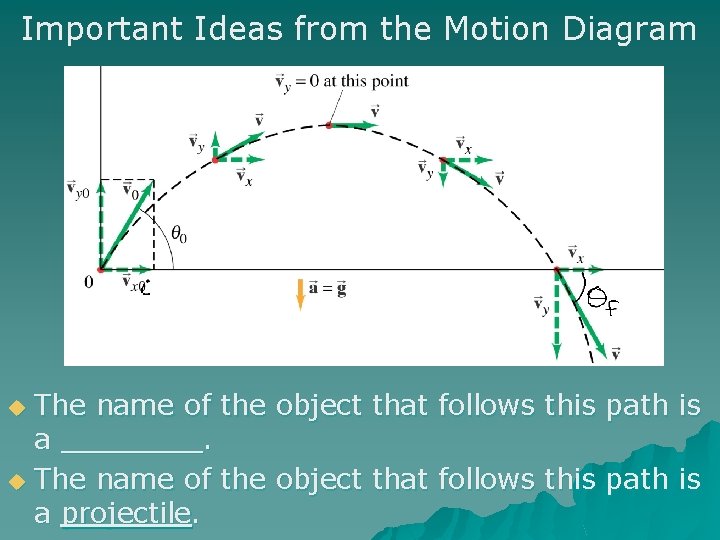
Important Ideas from the Motion Diagram The name of the object that follows this path is a ____. u The name of the object that follows this path is a projectile. u

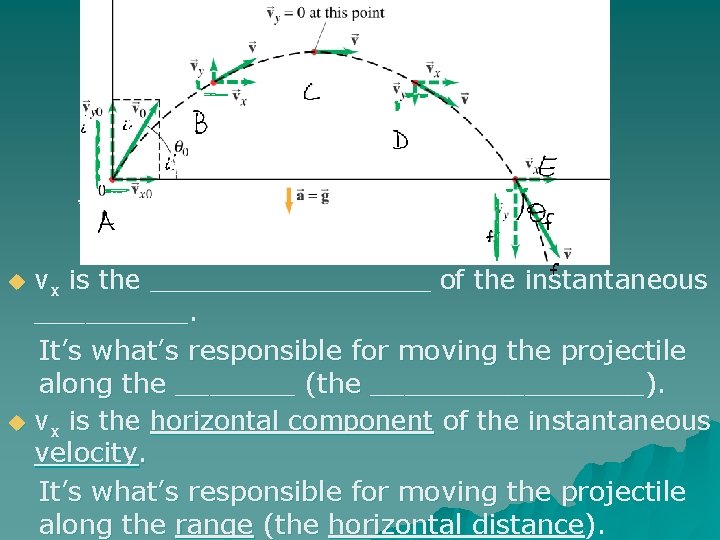
u u vx is the _________ of the instantaneous _____. It’s what’s responsible for moving the projectile along the _______ (the ________). vx is the horizontal component of the instantaneous velocity. It’s what’s responsible for moving the projectile along the range (the horizontal distance).

vy is the _________ of instantaneous velocity. It determines how ___, and therefore ______ it’s in the air. u vy is the vertical component of instantaneous velocity. It determines how high, and therefore how much time it’s in the air. u

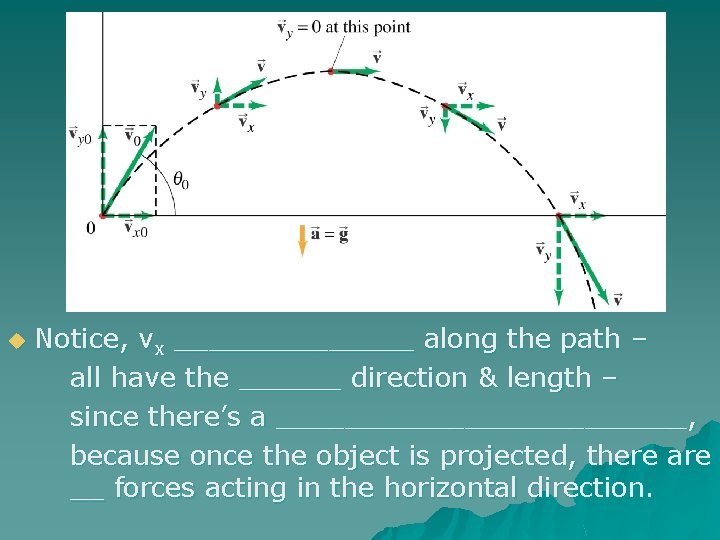
u Notice, vx _______ along the path – all have the ______ direction & length – since there’s a ____________, because once the object is projected, there are __ forces acting in the horizontal direction.

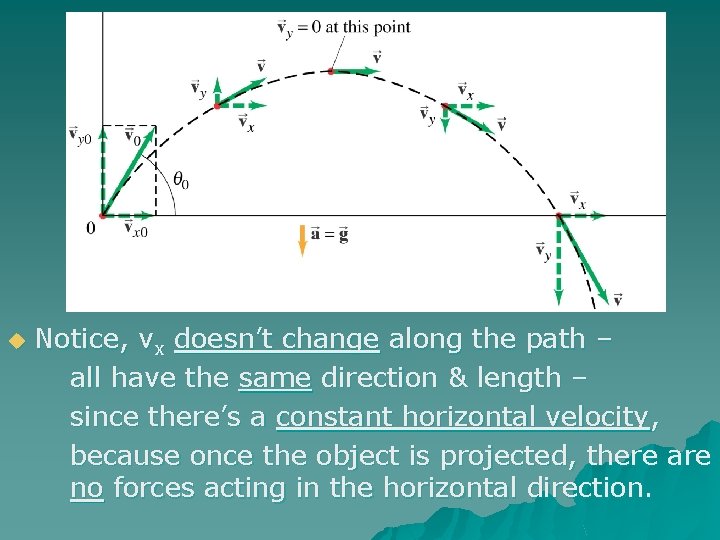
u Notice, vx doesn’t change along the path – all have the same direction & length – since there’s a constant horizontal velocity, because once the object is projected, there are no forces acting in the horizontal direction.

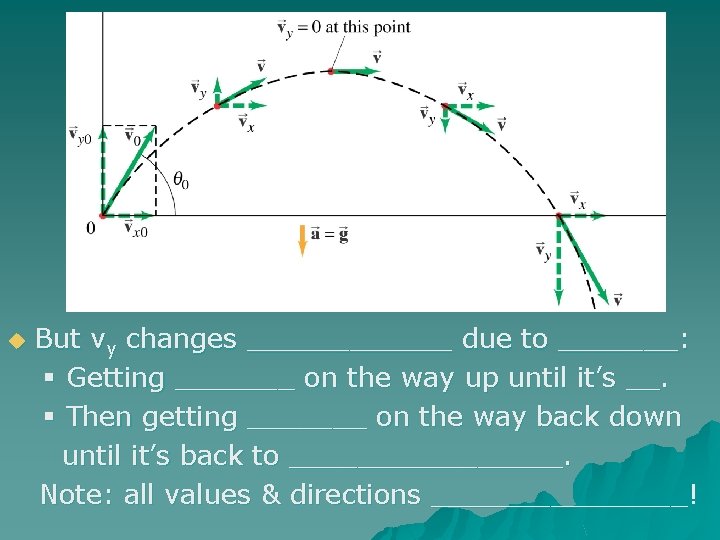
u But vy changes ______ due to _______: § Getting _______ on the way up until it’s __. § Then getting _______ on the way back down until it’s back to ________. Note: all values & directions ________!

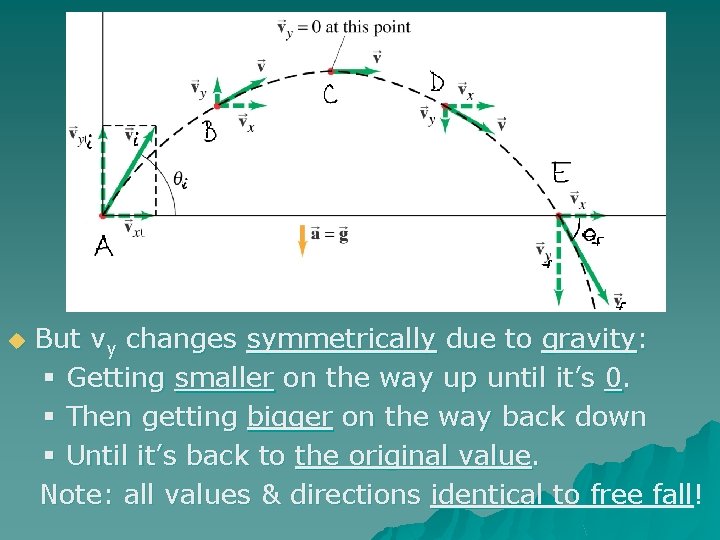
u But vy changes symmetrically due to gravity: § Getting smaller on the way up until it’s 0. § Then getting bigger on the way back down § Until it’s back to the original value. Note: all values & directions identical to free fall!

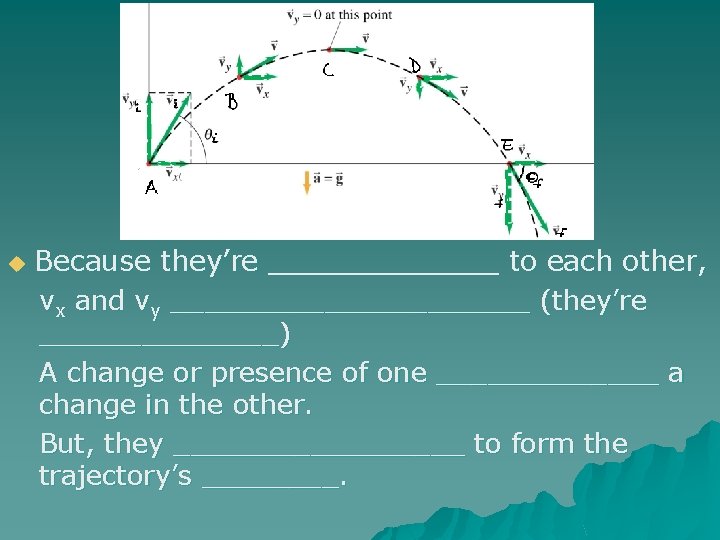
u Because they’re _______ to each other, vx and vy ___________ (they’re _______) A change or presence of one _______ a change in the other. But, they _________ to form the trajectory’s ____.

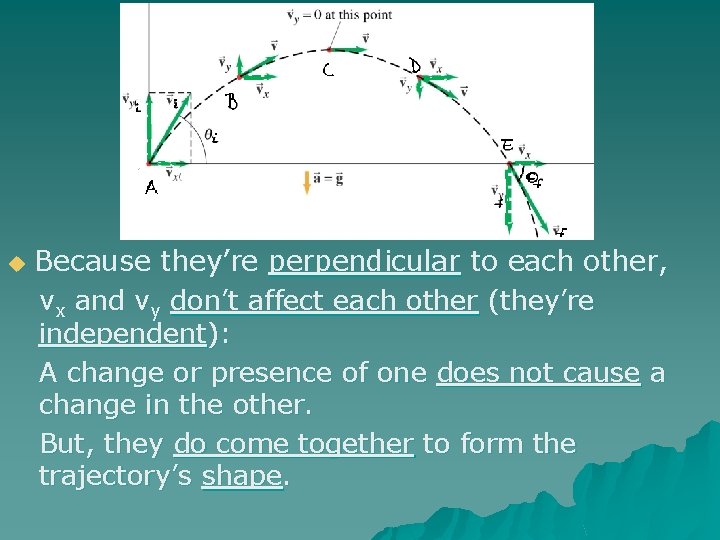
u Because they’re perpendicular to each other, vx and vy don’t affect each other (they’re independent): A change or presence of one does not cause a change in the other. But, they do come together to form the trajectory’s shape.

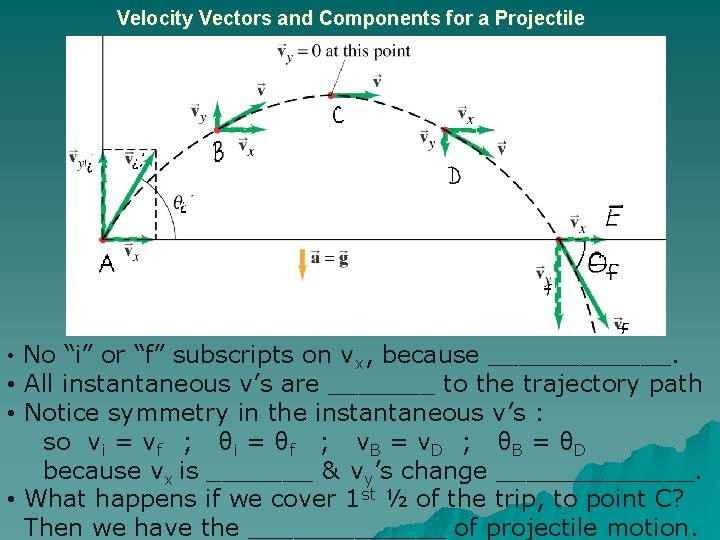
Velocity Vectors and Components for a Projectile • No “i” or “f” subscripts on vx, because ______. • All instantaneous v’s are _______ to the trajectory path • Notice symmetry in the instantaneous v’s : so vi = vf ; θi = θf ; v. B = v. D ; θB = θD because vx is _______ & vy’s change _______. • What happens if we cover 1 st ½ of the trip, to point C? Then we have the _______ of projectile motion.

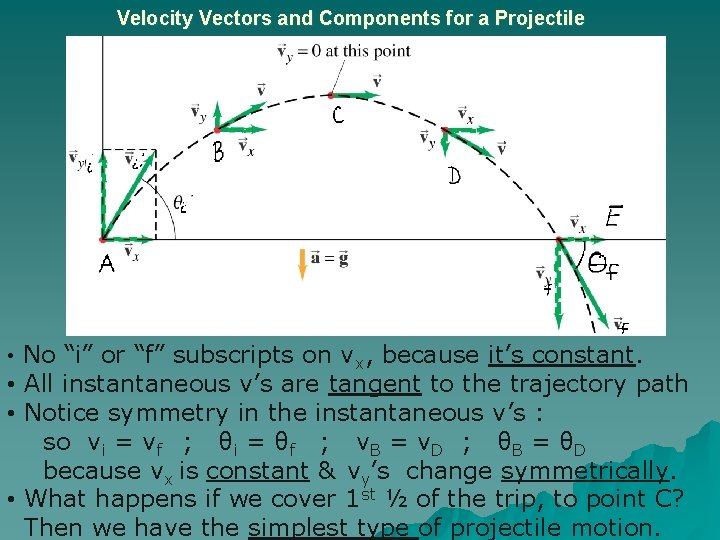
Velocity Vectors and Components for a Projectile • No “i” or “f” subscripts on vx, because it’s constant. • All instantaneous v’s are tangent to the trajectory path • Notice symmetry in the instantaneous v’s : so vi = vf ; θi = θf ; v. B = v. D ; θB = θD because vx is constant & vy’s change symmetrically. • What happens if we cover 1 st ½ of the trip, to point C? Then we have the simplest type of projectile motion.

Angles & Speed of Projection Don’t Matter! For any projectile, no matter the projection speed or angle, the vertical distance it falls beneath its imaginary straight line path (if there were no gravity) is the same as the vertical distance it would fall if simply dropped (in free fall) from rest! Why? ? Independence of perpendicular vectors!

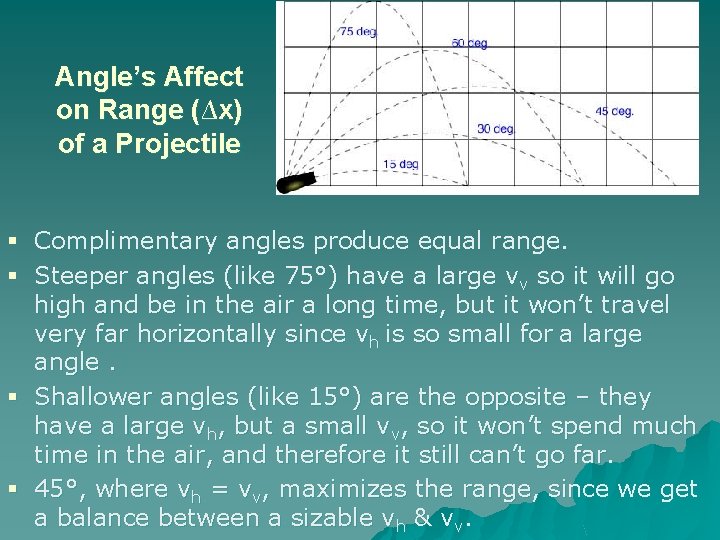
Angle’s Affect on Range (∆x) of a Projectile § Complimentary angles produce equal range. § Steeper angles (like 75°) have a large vv so it will go high and be in the air a long time, but it won’t travel very far horizontally since vh is so small for a large angle. § Shallower angles (like 15°) are the opposite – they have a large vh, but a small vv, so it won’t spend much time in the air, and therefore it still can’t go far. § 45°, where vh = vv, maximizes the range, since we get a balance between a sizable vh & vv.

Process for Solving Projectile Motion Problems 1. 2. 3. 4. ID your 2 given pieces of information and your unknown with proper variables: Δy, vh, Δx Which equation has the unknown in it? Δy = vvi Δt + ½ a Δt 2 or vh = Δx/ Δt But before you can use that equation to solve for your unknown, what value do you have to find first? ______. Use the other equation to find _______ 1 st. Now, with ______, go back and find the unknown using the equation you picked in Step #2.

Let’s try one: A marble rolls along a flat table with a speed of 1. 2 m/s. It rolls off the edge of the table and lands in a cup placed. 51 m away from the base of the table. Determine the height of the table. . 885 m or 88. 5 cm