Projectile Motion AIM how do we solve projectile

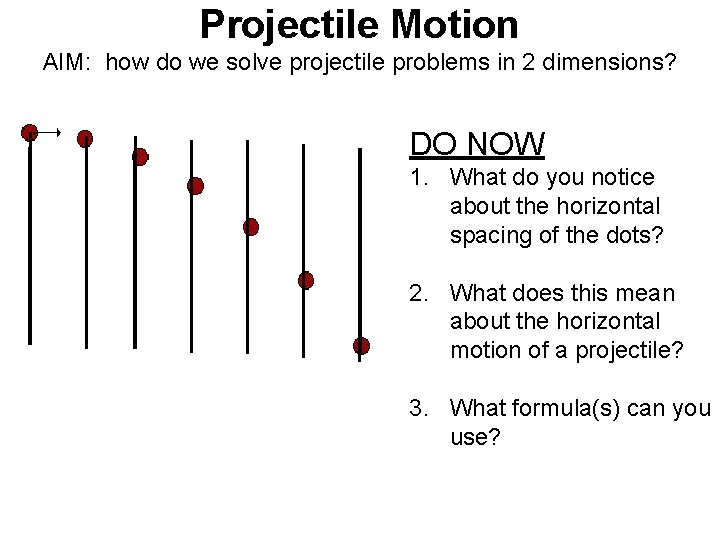
Projectile Motion AIM: how do we solve projectile problems in 2 dimensions? DO NOW 1. What do you notice about the horizontal spacing of the dots? 2. What does this mean about the horizontal motion of a projectile? 3. What formula(s) can you use?

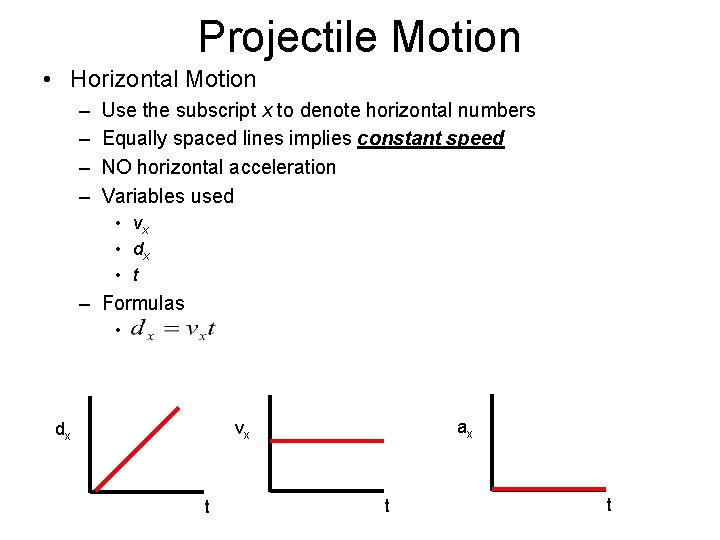
Projectile Motion • Horizontal Motion – – Use the subscript x to denote horizontal numbers Equally spaced lines implies constant speed NO horizontal acceleration Variables used • vx • dx • t – Formulas • ax vx dx t t t

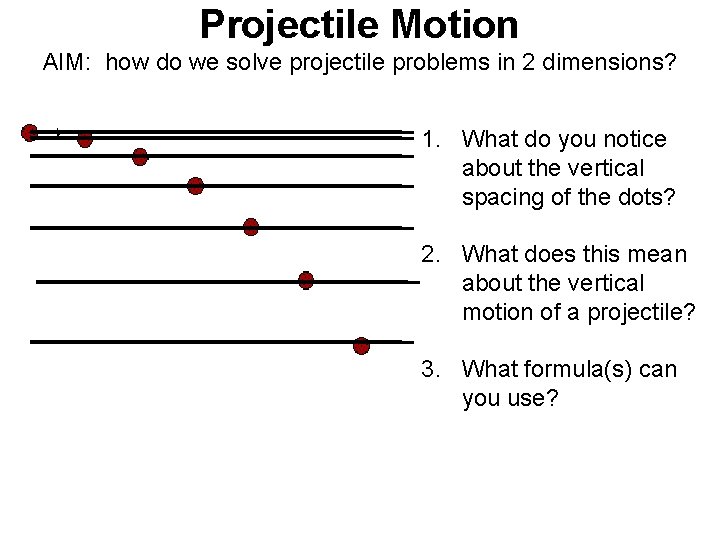
Projectile Motion AIM: how do we solve projectile problems in 2 dimensions? 1. What do you notice about the vertical spacing of the dots? 2. What does this mean about the vertical motion of a projectile? 3. What formula(s) can you use?

• Vertical Motion Projectile Motion – Use the subscript y to denote vertical numbers – Lines that get progressively farther apart imply vertical acceleration – Variables used • • • viy dy ay vfy t – Formulas • ay vy dy t t t

Projectile Rules 1. Vertical acceleration is always 9. 81 m/s 2 downwards for all objects at all times. 2. Horizontal acceleration is always zero. 3. You CAN NOT but a horizontal number in the same equation as a vertical number. 4. “thrown horizontally” means… - Viy is zero - “Dropped” means Viy is zero

Projectile Rules 5. An object dropped and launched horizontally from the same height will hit the floor at the same time. - Mass does not matter - Horizontal launch speed does not matter 6. Final velocity is NOT zero 7. Time is the only number that has no direction and can be used in any equation.

How to solve a projectile problem 1. Draw and label a diagram with every number they give you. 2. Make a list of all horizontal and vertical variables. KEEP THESE LISTS SEPARATE! 3. If you do not have time, find it! 4. Using the time found/given solve for the variable in question.

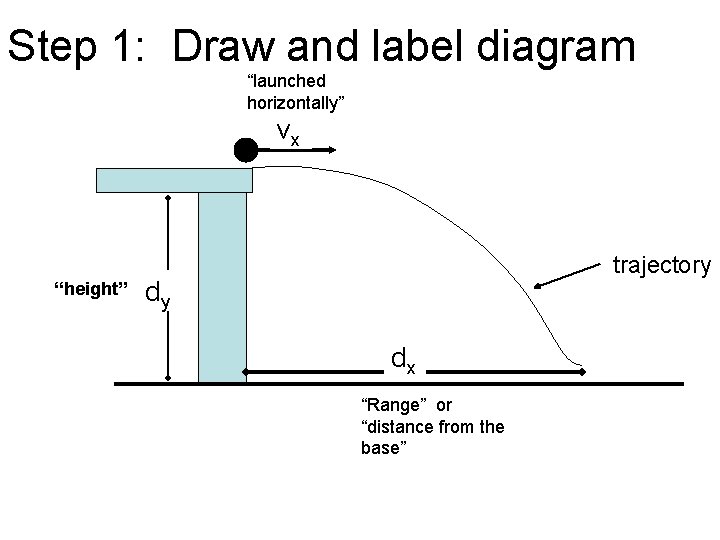
Step 1: Draw and label diagram “launched horizontally” vx “height” trajectory dy dx “Range” or “distance from the base”

Step 2: Separate variables We separate them because we cant mix them in equations!!!! Variable Chart Horizontal Motion (left and right) constant speed motion! Vertical Motion (up and down) constant acceleration! viy = ay = dy = t= vfy = vx = dx = t= d=vt

Step 3: Solve for the variables asked for • REMEMBER: – you can not mix horizontal and vertical variables! – only time is the same in both columns – there is no vi horizontally because the horizontal velocity is constant – There is also NO horizontal acceleration – The time of flight only depends on the vertical variables Bullet dropped vs. bullet fired • max time of flight is when an object is launched straight up! – maximum range is when an object is launched at 45 o to the horizontal.

1. A toy car moving at 3 m/s drives horizontally off of a 1. 5 m high table. a. How long is the car in the air for? b. How far away from the base of the table does the car land? 2. A set of keys is thrown horizontally at 12 m/s from a window that is 30 m high a. How long are the keys in the air? b. How far away from the base of the building do the keys hit the floor? c. What is the final vertical velocity of the keys? d. What is the final horizontal velocity of the keys? EXPLAIN! 3. A movie requires a car to drive horizontally off of a 50 m high building. If the stunt crew decides to place the airbag 15 m from the base of the building A. How fast should the car drive off the building? B. What would happen if the car drove off slower? C. What would happen if the car drove off faster? D. What would happen if the movie director decided he wanted to use a truck instead of a car? Would the stunt crew have to change the location of the air bag or tell the truck to drive at a different speed? DEFEND YOUR ANSWER!

4. A motorcycle drives horizontally off of a cliff that is 25 m high and is found 85 m from the base of the cliff. If the speed limit on the road is 35 m/s, was the motorcycle speeding? (assume the motorcycle didn’t skid after landing) 5. A rifle is shot perfectly horizontally and the bullet leaves the barrel of the gun at 100 m/s. a. If the bullet is found 1. 2 km away from the gun, how high was the gun mounted off the ground? b. If the muzzle of the gun is 20 cm long, what is the acceleration of the bullet while in the muzzle of the gun? c. How long is the bullet in the gun for? d. How long is the bullet in the air for?

6. You take a running start and jump horizontally off the roof of your house that is 12 m high in an attempt to land on the roof of the building next door that is 7 m tall. The horizontal spacing between the buildings is 6 m. If you can run at 6. 2 m/s, do you make it?

Projectiles Launched at an Angle on Level Ground vi θ

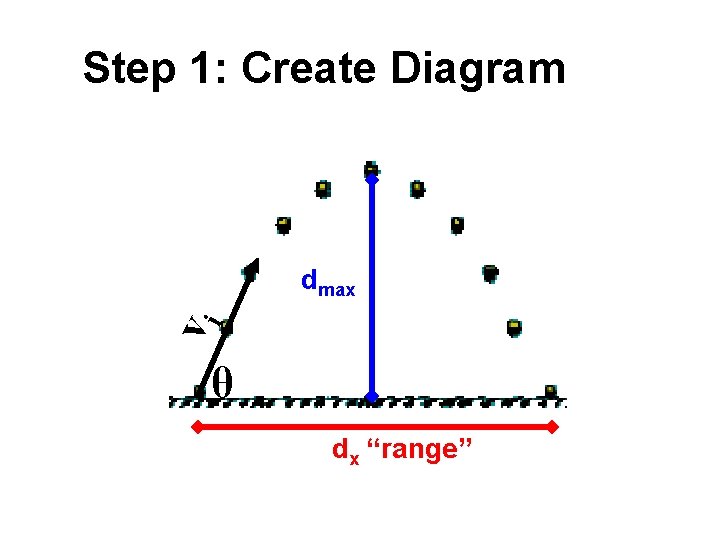
Step 1: Create Diagram vi dmax θ dx “range”

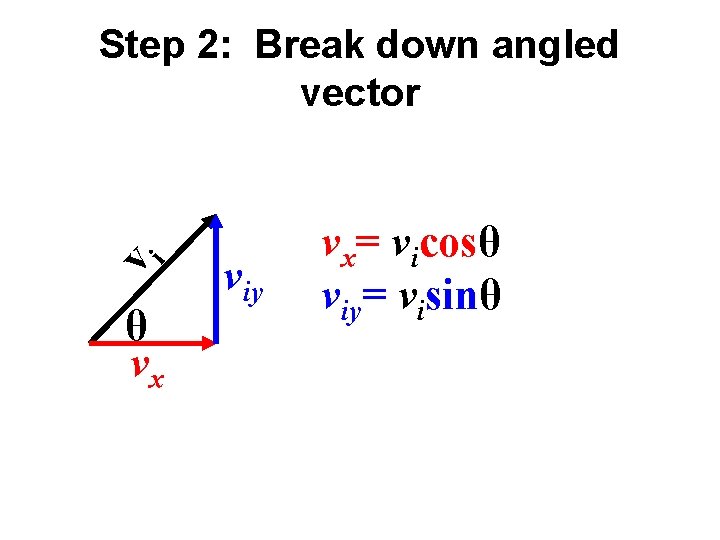
i v Step 2: Break down angled vector θ vx viy vx= vicosθ viy= visinθ

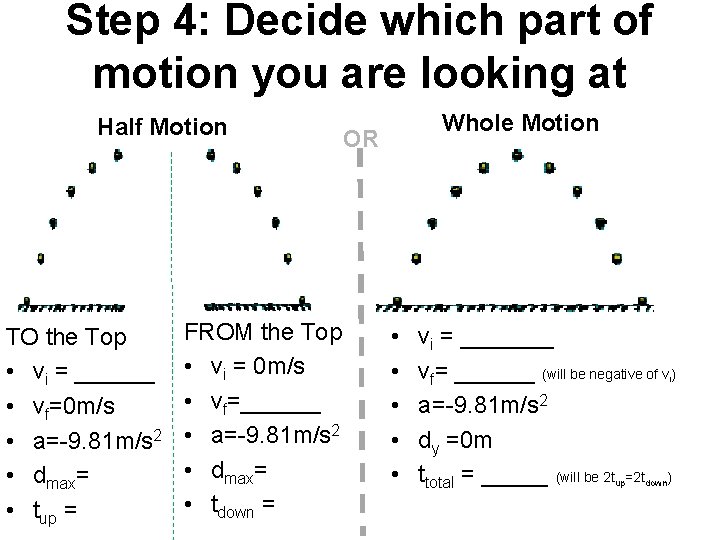
Step 4: Decide which part of motion you are looking at Half Motion TO the Top • vi = ______ • vf=0 m/s • a=-9. 81 m/s 2 • dmax= • tup = FROM the Top • vi = 0 m/s • vf=______ • a=-9. 81 m/s 2 • dmax= • tdown = Whole Motion OR • • • vi = _______ vf= ______ (will be negative of v ) a=-9. 81 m/s 2 dy =0 m ttotal = _____ (will be 2 t =2 t ) i up down

Step 3: Separate variables into horizontal and vertical then solve Horizontal Motion (left and right) constant speed motion! Vertical Motion (up and down) constant acceleration! viy = ay = dy = t= vfy = vx = dx = t= d=vt

4. A motorcycle moving at 35 m/s drives off a ramp that makes an angle of 50 o to the horizontal. If the motorcycle lands at the same height it jumped from - What is the motorcycle’s mat height? - How long is the motorcycle in the air for? - How far away from the jump point does the motorcycle land? 5. During a soccer game, the goalie kicks a goal kick at 28 m/s at an angle of 50 o above the horizontal. How far from the goalie does the ball land? 6. During a football game, the kicker attempts a field goal that is 50 m from the goal post which are 4 m above the ground. The kicker kicks the ball at 22 m/s at an angle of 42 o above the horizontal. Assuming he aims on target, is the field goal good? If not why?

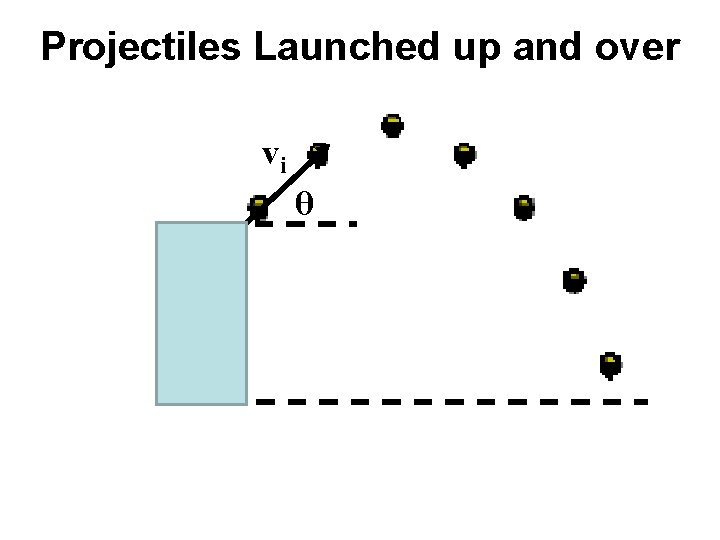
Projectiles Launched up and over vi θ

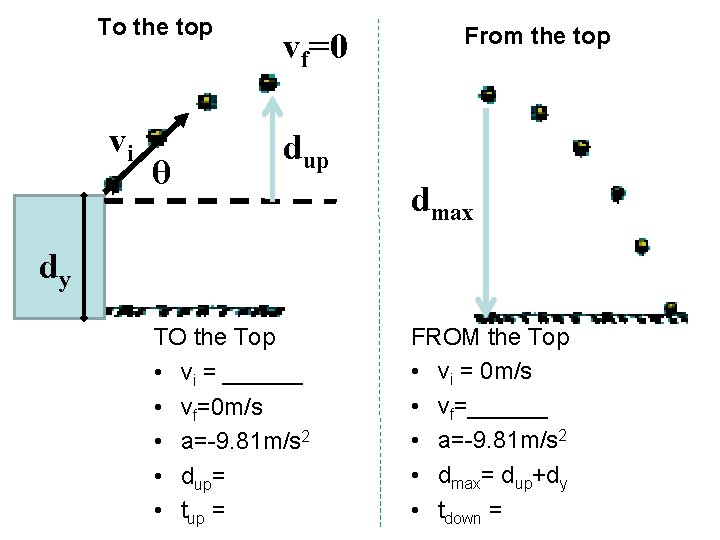
To the top vi θ vf=0 From the top dup dmax dy TO the Top • vi = ______ • vf=0 m/s • a=-9. 81 m/s 2 • dup= • tup = FROM the Top • vi = 0 m/s • vf=______ • a=-9. 81 m/s 2 • dmax= dup+dy • tdown =

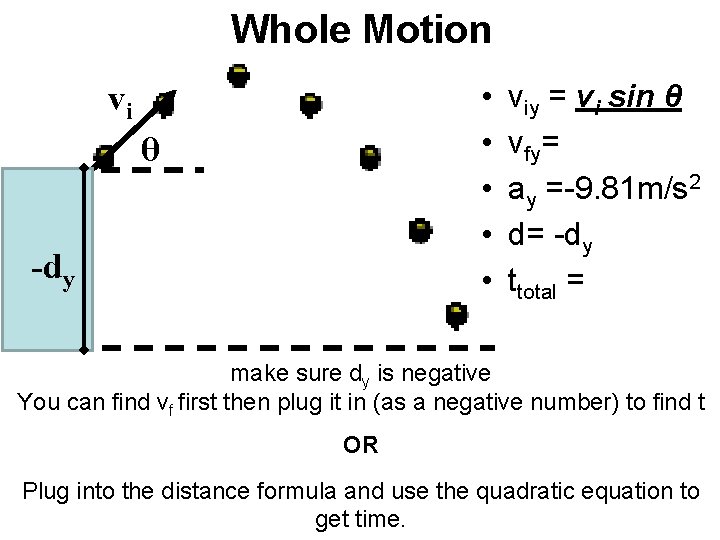
Whole Motion • • • vi θ -dy viy = vi sin θ vfy= ay =-9. 81 m/s 2 d= -dy ttotal = make sure dy is negative You can find vf first then plug it in (as a negative number) to find t OR Plug into the distance formula and use the quadratic equation to get time.

6. You take a running start and jump off the roof of your house that is 12 m above the ground. You can run at a speed of 5 m/s and jump at an angle of 60 o to the horizontal. a. How long are you in the air for? b. How far from the base of the house do you land?

7. A set of keys is thrown at 12 m/s 35 o above the horizontal from a window that is 30 m high a. How long are the keys in the air? b. How far away from the base of the building do the keys hit the floor? c. What is the final vertical velocity of the keys? d. What is the final horizontal velocity of the keys? EXPLAIN!