Project Part III Scarlitte Ponce Starlitte Ponce Cristina

Project Part III Scarlitte Ponce Starlitte Ponce Cristina Hernandez

9. Each of (a)–(c) describes a graph. In each case answer yes, no, or not necessarily to this question: Doesthe graph have an Euler circuit? Justify your answers. a. G is a connected graph with five vertices of degrees 2, 2, 3, 3, and 4. b. G is a connected graph with five vertices of degrees 2, 2, 4, 4, and 6. c. G is a graph with five vertices of degrees 2, 2, 4, 4, and 6.

a) No. This graph has two vertices of odd degree, whereas all vertices of a graph with an Euler circuit have even degree b) Yes. This graph has five vertices of even degree just like a Euler circuit. c)Yes. This graph has five vertices of even degree just like a Euler circuit.

Explanation : # 9 Eulerian circuit or Eulerian circuit is an Eulerian which starts and ends on the same vertex. They were first discussed by Leonward Eular while solving the famous Seven Bridges of Kongeonsoki problem in 1736. Euler theory was that, is it possible to construct a path or a circuit starting and ending on the same vertex, which visits each edge exactly once. condition for it to be a eular circuit is condition: If a graph has any vertices of odd degree, then it CANNOT have a eular circuit AND If a graph is connected and every vertex has even degree, then it has AT LEAST ONE EULER CIRCUIT IN this case according to Eular condition for it to be a euler Circuit the only one with a problem is a) which as two vertices with odd degees is not a eular circuit and b) and C) are applied becasue all their vertices have an even degree

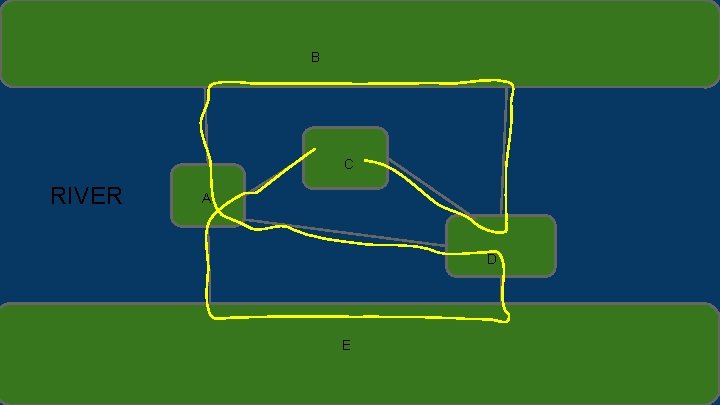
18. Is it possible to take a walk around the city whose map is shown below, starting and ending at the same point and crossing each bridge exactly once? If so, how can this be done? Yes, this is called an Euler Circuit. A Euler circuit exists in a graph G when that circuit contains every vertex and every edge of G. It is a sequence of adjacent vertices and edges that has at least one of the edges, starts and ends at the same vertex, uses every vertex of G at least once, and uses every edge of G only once. Another note about an Euler circuit is that every vertex in the graph has a positive even degree. If any of the vertices have an odd degree then that graph does not have an Euler circuit, this is called the contrapositive version of the Euler circuit theorem.

B B C RIVER A D E E