Project Management of large scale projects challenging Coordinate

Project Management of large scale projects – challenging? ? Coordinate numerous activities Network techniques (like CPM, PERT) are of aid Examples and applications q Construction of a new manufacturing plant q R&D of a new product q Ship-building

Project Management Examples and applications q Movie production q Relocation of a facility (e. g. , warehouse) q Maintenance of a nuclear reactor q Installation of an MIS / ERP system q Conducting marketing research / advertising campaign What is a project? Collection of inter-related activities consuming time/resources

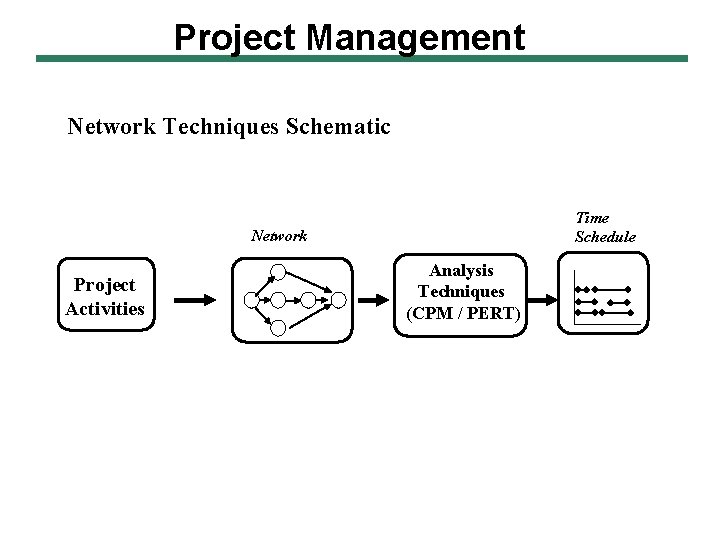
Project Management Network Techniques Schematic Time Schedule Network Project Activities Analysis Techniques (CPM / PERT)

Project Management Network Representation of a Project Activities = Arc Events = Nodes Rule 1 Each activity represented by one and only one arrow in the network Rule 2 Each activity identified by 2 distinct end nodes Rule 3 Correct precedence of activity A requires knowledge of activities following A à preceding A concurrent with A Rule 4 Dummy activities can be used to ensure proper precedence and concurrence (dummy activity does not require any time / resource)

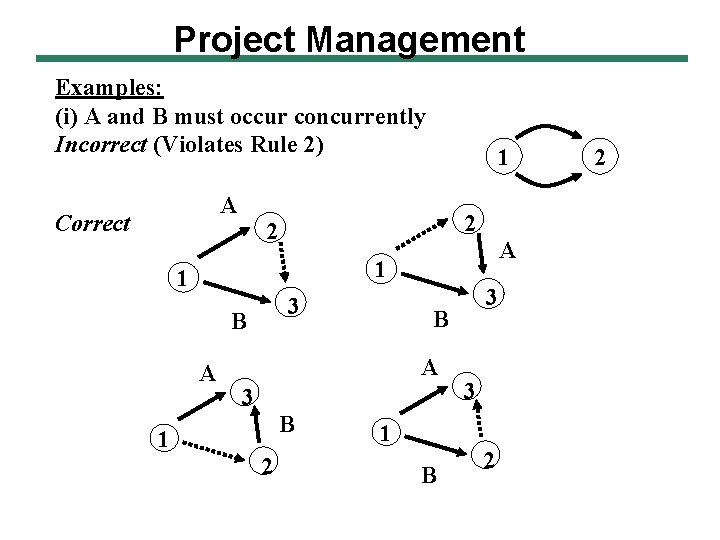
Project Management Examples: (i) A and B must occur concurrently Incorrect (Violates Rule 2) A Correct 1 2 2 A 1 1 3 B A 3 B 1 2 3 3 1 B 2 2

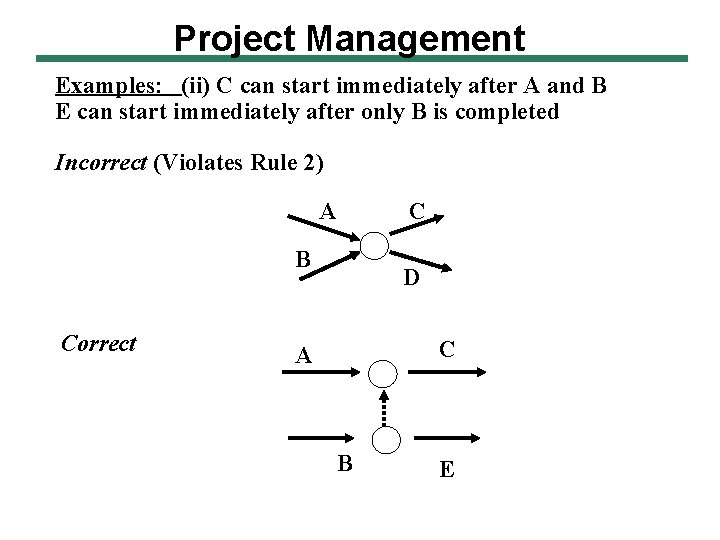
Project Management Examples: (ii) C can start immediately after A and B E can start immediately after only B is completed Incorrect (Violates Rule 2) A C B Correct D C A B E

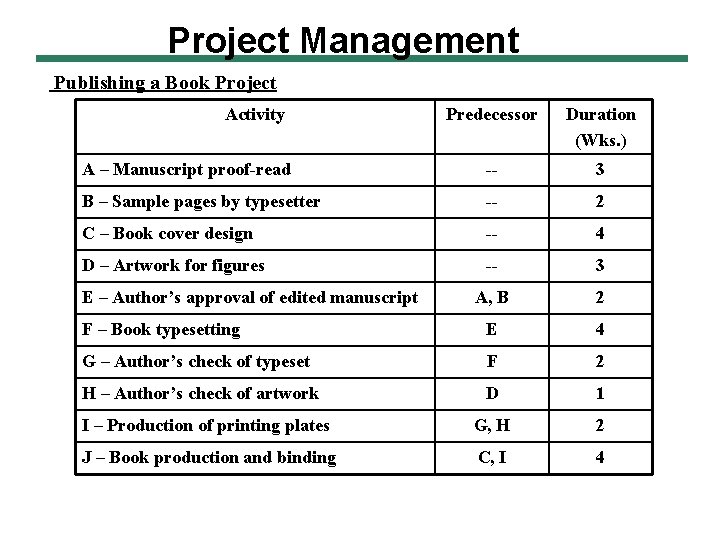
Project Management Publishing a Book Project Activity Predecessor Duration (Wks. ) A – Manuscript proof-read -- 3 B – Sample pages by typesetter -- 2 C – Book cover design -- 4 D – Artwork for figures -- 3 A, B 2 F – Book typesetting E 4 G – Author’s check of typeset F 2 H – Author’s check of artwork D 1 I – Production of printing plates G, H 2 J – Book production and binding C, I 4 E – Author’s approval of edited manuscript

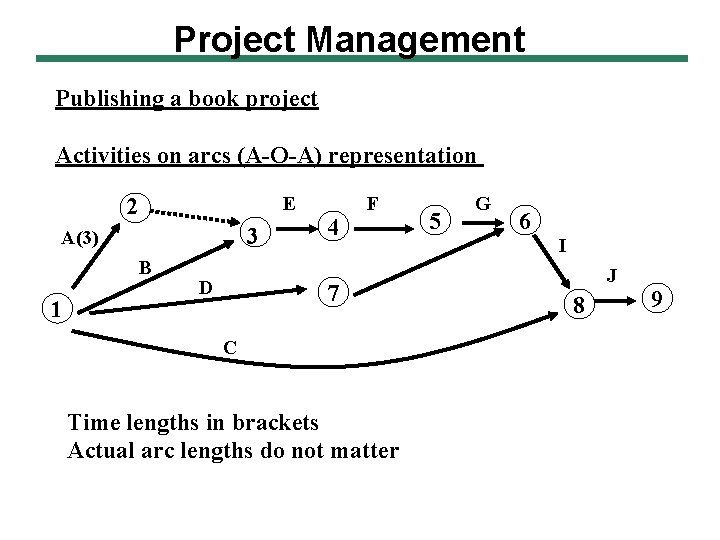
Project Management Publishing a book project Activities on arcs (A-O-A) representation E 2 3 A(3) B 1 D 4 F 7 C Time lengths in brackets Actual arc lengths do not matter 5 G 6 I J 8 9

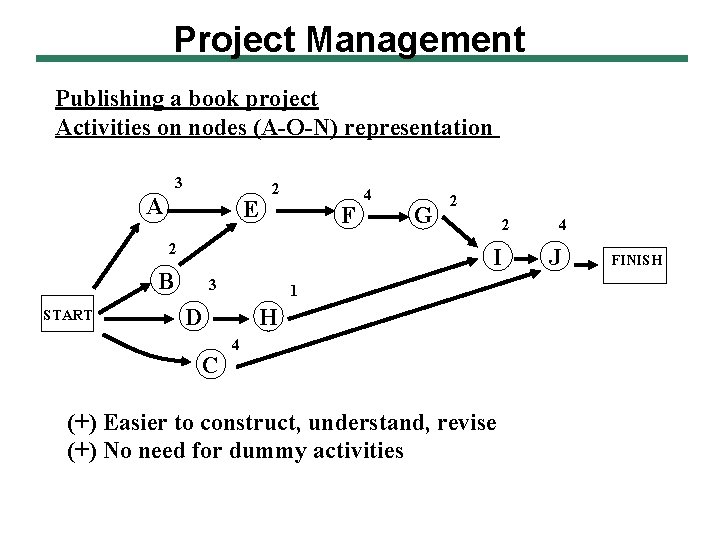
Project Management Publishing a book project Activities on nodes (A-O-N) representation 3 A E 2 F 2 G 2 2 I B START 4 3 1 D C H 4 (+) Easier to construct, understand, revise (+) No need for dummy activities 4 J FINISH

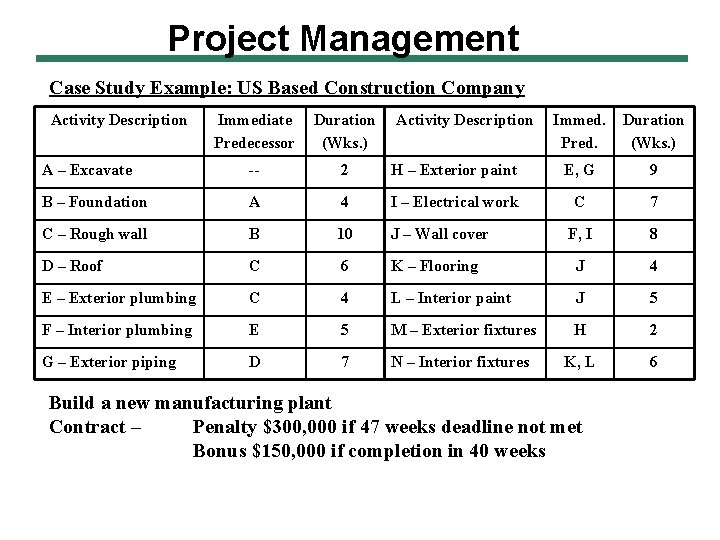
Project Management Case Study Example: US Based Construction Company Activity Description Immediate Predecessor Duration (Wks. ) A – Excavate -- 2 B – Foundation A C – Rough wall Activity Description Immed. Pred. Duration (Wks. ) H – Exterior paint E, G 9 4 I – Electrical work C 7 B 10 J – Wall cover F, I 8 D – Roof C 6 K – Flooring J 4 E – Exterior plumbing C 4 L – Interior paint J 5 F – Interior plumbing E 5 M – Exterior fixtures H 2 G – Exterior piping D 7 N – Interior fixtures K, L 6 Build a new manufacturing plant Contract – Penalty $300, 000 if 47 weeks deadline not met Bonus $150, 000 if completion in 40 weeks

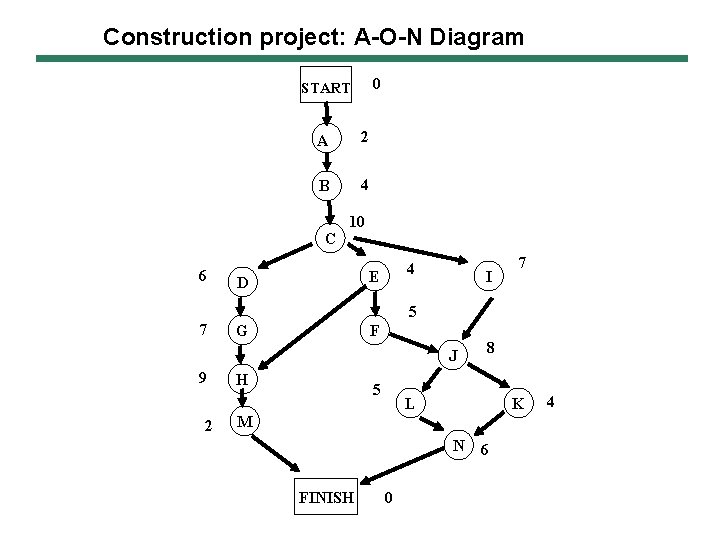
Construction project: A-O-N Diagram 0 START A 2 B 4 C 6 10 4 E D I 7 5 7 G F J 9 2 H 5 8 L K M N FINISH 0 6 4

Construction project: Questions of interest 1) Total time, if no delays occur? 2) When should individual activities start and finish in view of 1 (at the latest)? 3) When should individual activities start and finish in view of 1 (at the earliest)? 4) Critical bottleneck activities? 5) For other activities, how much delay is permissible without causing delays? 6) If activity timings are uncertain, probability of completion of the project by deadline? 7) If extra money is used to expedite the project, which is the least expensive way of doing so?

The notion of critical path Path – routes from START FINISH Length of Path – sum of activity duration Path Length (Weeks) START – A B C D G H M -- FINISH 40 START – A B C E H M -- FINISH 31 START – A B C E F J K N -- FINISH 43 START – A B C E F J L N -- FINISH 44 START – A B C I J K N -- FINISH 41 START – A B C I J L N -- FINISH 42 Longest path

The notion of critical path Reasoning q Project duration cannot be shorter than any of the above paths q It can be longer than some paths q Cannot be longer than ONE path – longest path q All the shorter paths will reach FINISH no later than this path q This path has the property that if any activity is delayed on this path, then the entire project duration will increase CRITICAL PATH q Since enumerating all the paths might be difficult for large networks CRITICAL PATH METHOD (CPM) Starts by answering Q. 2 and 3 of the list.

Determining est, eft Earliest Start Time (EST) Rule: EST of an activity = Largest EFT of its immediate predecessors EFT Rule: EFT = EST + Activity duration EST = EFT = 0 for START node The calculations for this are begun from START and end at FINISH FORWARD PASS

Determining lst, lft Latest Finish Time (LFT) Rule: LFT of an activity = Smallest LST of its immediate successors LST Rule: LST = LFT - Activity duration LFT = EFT for FINISH node The calculations for this are begun from FINISH and end at START BACKWARD PASS

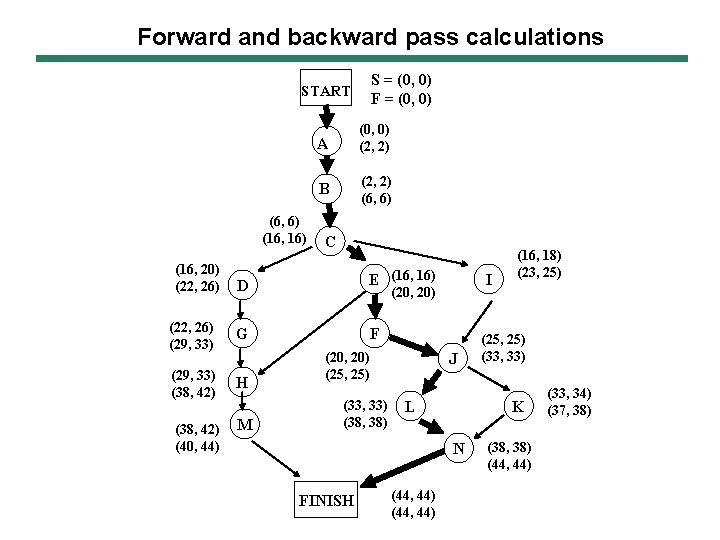
Forward and backward pass calculations S = (0, 0) F = (0, 0) START (6, 6) (16, 16) (16, 20) (22, 26) A (0, 0) (2, 2) B (2, 2) (6, 6) C D E (16, 16) (22, 26) (29, 33) G F (29, 33) (38, 42) H (38, 42) (40, 44) M I (20, 20) J (20, 20) (25, 25) (33, 33) (38, 38) L (44, 44) (25, 25) (33, 33) K N FINISH (16, 18) (23, 25) (38, 38) (44, 44) (33, 34) (37, 38)

Determining slack in the schedule Slack for an activity = LFT - EFT Those activities for which slack is zero are on critical path because they must finish by EFT For other activities, there is some flexibility in scheduling, which is equal to slack The above analysis answers Q. 1 – 5 (For A-O-A networks, there is a similar term FLOAT equivalent to slack. Dij i j Total float = LSTj – LSTi – Dij Free float = ESTj – ESTi – Dij )

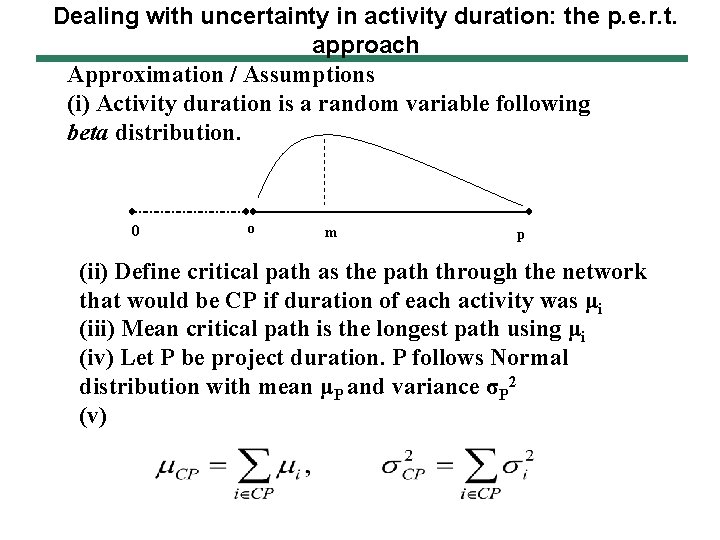
Dealing with uncertainty in activity duration: the p. e. r. t. approach This answers Q. 6 Suppose we are interested in the question: What is the probability of completing the project by the deadline of 47 weeks? PERT approach - (o, m, p) = (optimistic time estimate, most likely, pessimistic) Approximation / Assumptions (i) Activity duration is a random variable following beta distribution

Dealing with uncertainty in activity duration: the p. e. r. t. approach Approximation / Assumptions (i) Activity duration is a random variable following beta distribution. 0 o m p (ii) Define critical path as the path through the network that would be CP if duration of each activity was μi (iii) Mean critical path is the longest path using μi (iv) Let P be project duration. P follows Normal distribution with mean μP and variance σP 2 (v)

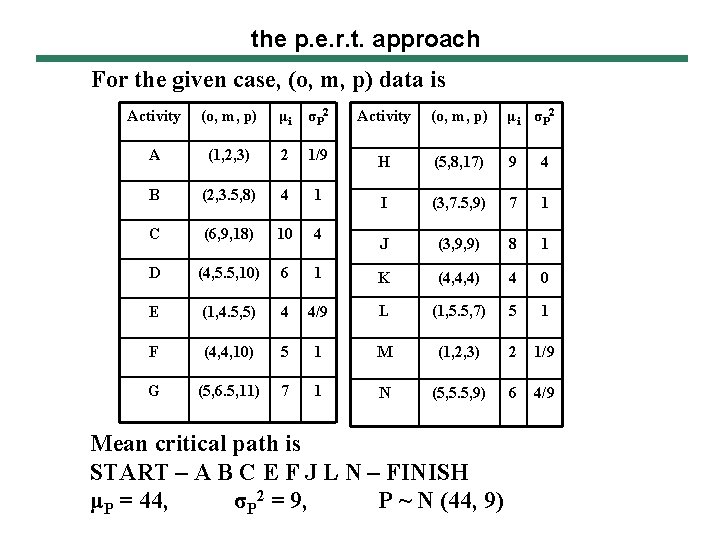
the p. e. r. t. approach For the given case, (o, m, p) data is Activity (o, m, p) μi σP 2 A (1, 2, 3) 2 1/9 H (5, 8, 17) 9 4 B (2, 3. 5, 8) 4 1 I (3, 7. 5, 9) 7 1 C (6, 9, 18) 10 4 J (3, 9, 9) 8 1 D (4, 5. 5, 10) 6 1 K (4, 4, 4) 4 0 E (1, 4. 5, 5) 4 4/9 L (1, 5. 5, 7) 5 1 F (4, 4, 10) 5 1 M (1, 2, 3) 2 1/9 G (5, 6. 5, 11) 7 1 N (5, 5. 5, 9) 6 4/9 Mean critical path is START – A B C E F J L N – FINISH μP = 44, σP 2 = 9, P ~ N (44, 9)

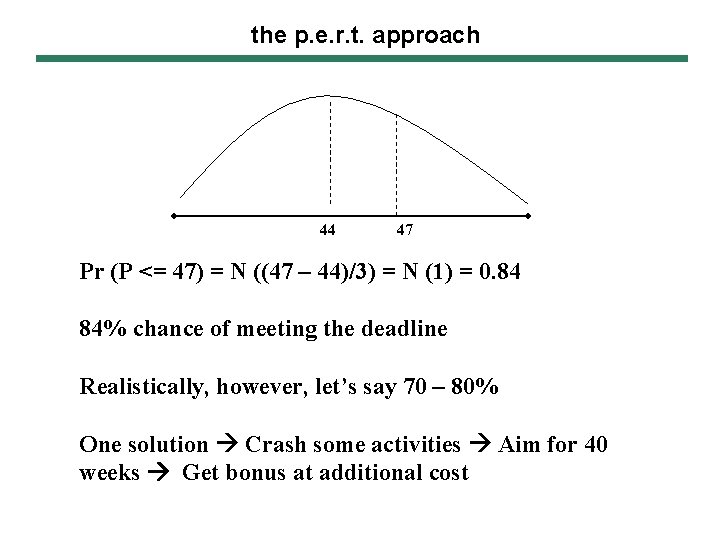
the p. e. r. t. approach 44 47 Pr (P <= 47) = N ((47 – 44)/3) = N (1) = 0. 84 84% chance of meeting the deadline Realistically, however, let’s say 70 – 80% One solution Crash some activities Aim for 40 weeks Get bonus at additional cost

Time – cost trade off Activity Cost Crash (C) Normal (N) Answer to Q. 7 Need to look at time-cost trade off data Activity Duration

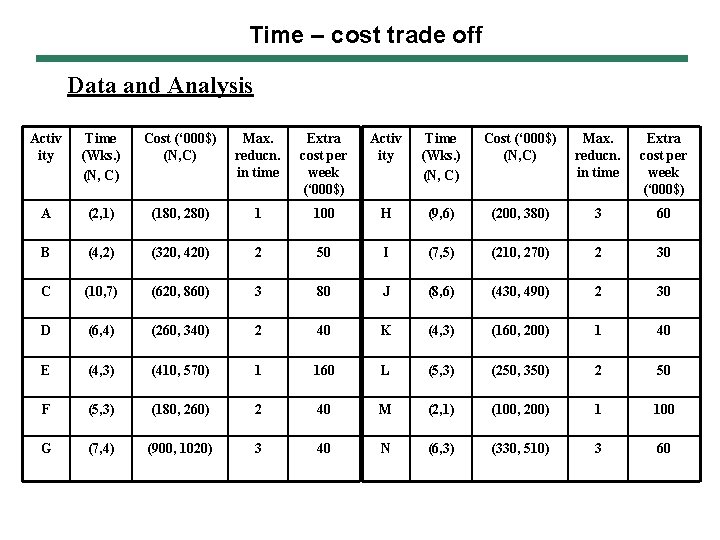
Time – cost trade off Data and Analysis Activ ity Time (Wks. ) (N, C) Cost (‘ 000$) (N, C) Max. reducn. in time Extra cost per week (‘ 000$) A (2, 1) (180, 280) 1 100 H (9, 6) (200, 380) 3 60 B (4, 2) (320, 420) 2 50 I (7, 5) (210, 270) 2 30 C (10, 7) (620, 860) 3 80 J (8, 6) (430, 490) 2 30 D (6, 4) (260, 340) 2 40 K (4, 3) (160, 200) 1 40 E (4, 3) (410, 570) 1 160 L (5, 3) (250, 350) 2 50 F (5, 3) (180, 260) 2 40 M (2, 1) (100, 200) 1 100 G (7, 4) (900, 1020) 3 40 N (6, 3) (330, 510) 3 60

Time – cost trade off Answer to Q. 7 Full crashing can complete the project in 28 weeks (on the path ABCEFJLN), but will also cost an extra $1. 6 million. If all activities are crashed, total cost = $6. 15 million If all activities are normal, total cost = $4. 55 million Difference = 6. 15 – 4. 55 = $1. 6 million SOLUTION: PARTIAL CRASHING. Which activities?

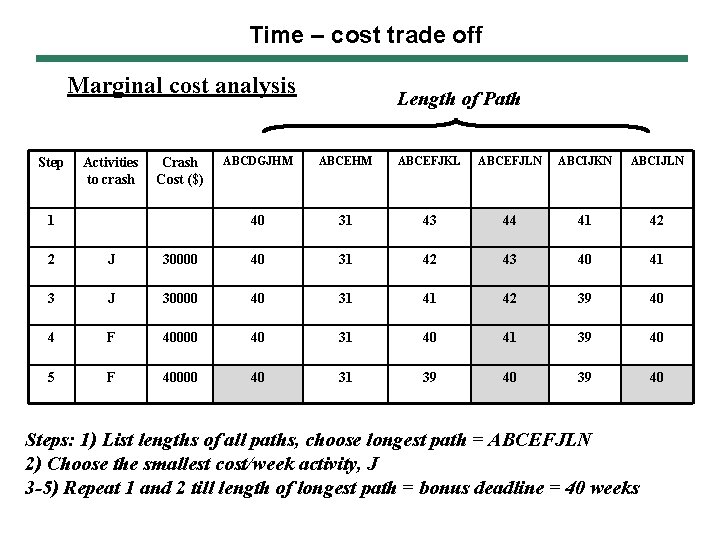
Time – cost trade off Marginal cost analysis Step Activities to crash Cost ($) 1 Length of Path ABCDGJHM ABCEFJKL ABCEFJLN ABCIJKN ABCIJLN 40 31 43 44 41 42 2 J 30000 40 31 42 43 40 41 3 J 30000 40 31 41 42 39 40 4 F 40000 40 31 40 41 39 40 5 F 40000 40 31 39 40 Steps: 1) List lengths of all paths, choose longest path = ABCEFJLN 2) Choose the smallest cost/week activity, J 3 -5) Repeat 1 and 2 till length of longest path = bonus deadline = 40 weeks

Time – cost trade off If we still have to go further, since there is a tie between 1 st, 4 th and 6 th paths, we will look for the lowest cost/unit activity amongst all paths. At this point, however, total cost of crashing = $140, 000. Since bonus is $150, 000 go for crashing A LP formulation of the above is possible and gives more efficient results.