Project Management Chapter 8 Crashing Copyright 2010 Pearson

Project Management Chapter 8 (Crashing) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 8 -1

Project Crashing Basic Concept In last lecture, we studied on how to use CPM and PERT to identify critical path for a project problem Now, the question is: Question: Can we cut short its project completion time? If so, how! Chapter 8 - Project Management 2 8 -2

Project Crashing Solution! Yes, the project duration can be reduced by assigning more resources to project activities. But, doing this would somehow increase our project cost! How do we strike a balance? ■ Project crashing is a method for shortening project duration by reducing one or more critical activities to a time less than normal activity time. 3 8 -3

Trade-off concept Here, we adopt the “Trade-off” concept n We attempt to “crash” some “critical” events by allocating more resources to them, so that the time of one or more critical activities is reduced to a time that is less than the normal activity time. n How to do that: n Question: What criteria should it be based on when deciding to crashing critical times? 4 8 -4

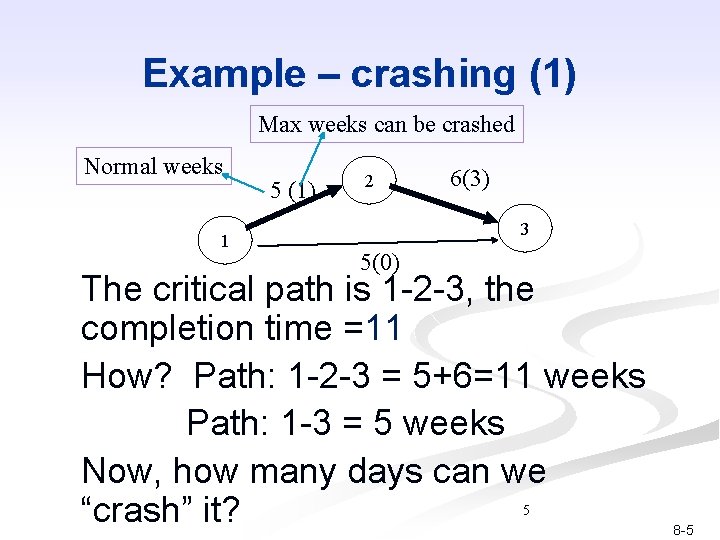
Example – crashing (1) Max weeks can be crashed Normal weeks 1 5 (1) 2 6(3) 3 5(0) The critical path is 1 -2 -3, the completion time =11 How? Path: 1 -2 -3 = 5+6=11 weeks Path: 1 -3 = 5 weeks Now, how many days can we “crash” it? 5 8 -5

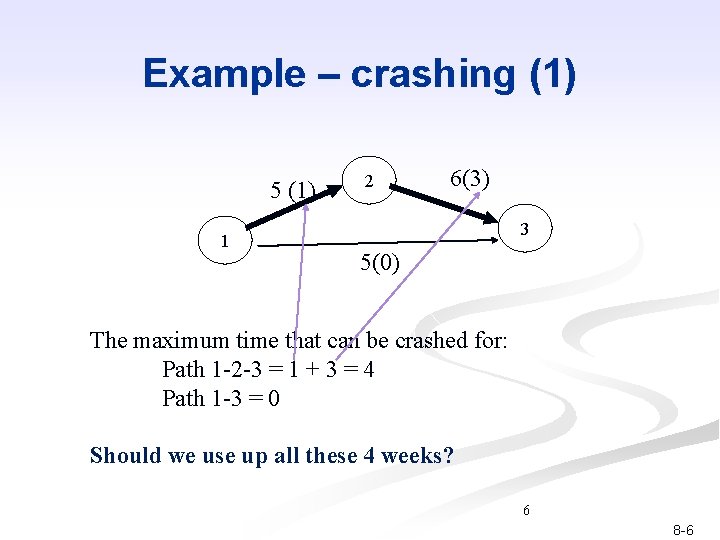
Example – crashing (1) 5 (1) 1 2 6(3) 3 5(0) The maximum time that can be crashed for: Path 1 -2 -3 = 1 + 3 = 4 Path 1 -3 = 0 Should we use up all these 4 weeks? 6 8 -6

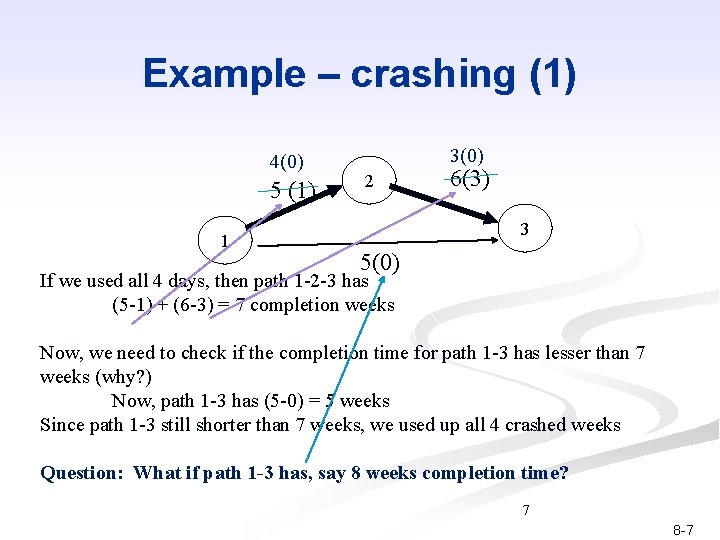
Example – crashing (1) 4(0) 5 (1) 1 3(0) 2 6(3) 3 5(0) If we used all 4 days, then path 1 -2 -3 has (5 -1) + (6 -3) = 7 completion weeks Now, we need to check if the completion time for path 1 -3 has lesser than 7 weeks (why? ) Now, path 1 -3 has (5 -0) = 5 weeks Since path 1 -3 still shorter than 7 weeks, we used up all 4 crashed weeks Question: What if path 1 -3 has, say 8 weeks completion time? 7 8 -7

Example – crashing (1) Such as 5 (1) 1 2 6(3) 3 8(0) Now, we cannot use all 4 days (Why? ) Because path 1 -2 -3 will not be critical path anymore as path 1 -3 would now has longest hour to finish Rule: When a path is a critical path, it will not stay as a critical path So, we can only reduce the path 1 -2 -3 completion time to the same time as path 1 -3. (HOW? ) 8 8 -8

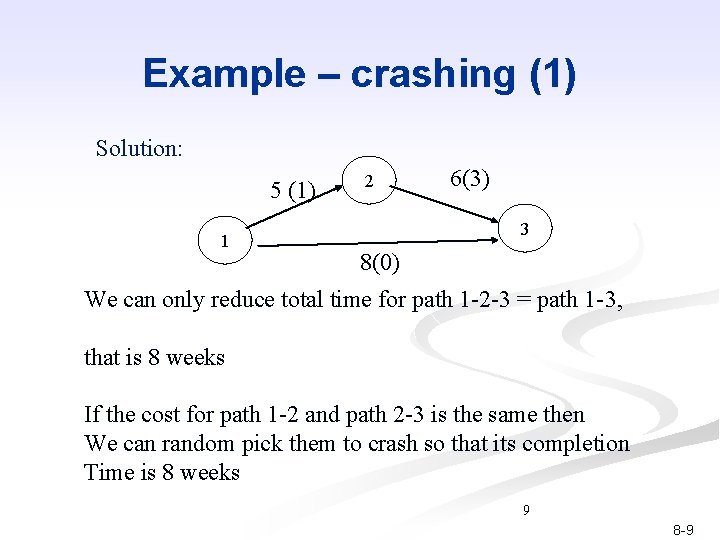
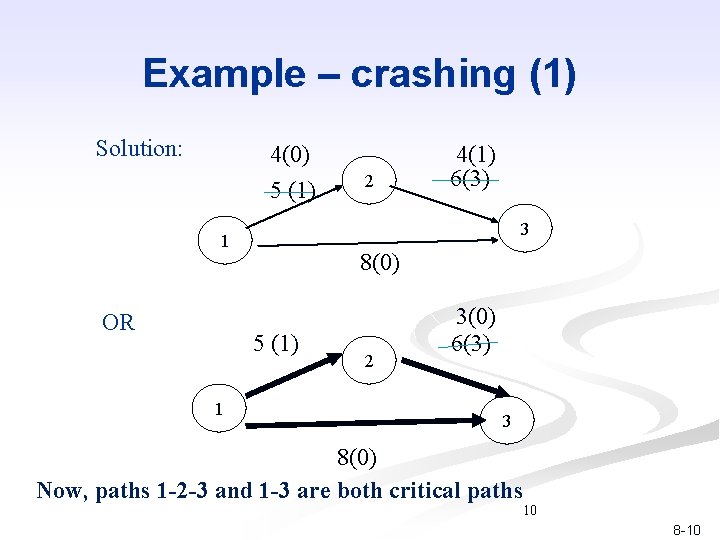
Example – crashing (1) Solution: 5 (1) 1 2 6(3) 3 8(0) We can only reduce total time for path 1 -2 -3 = path 1 -3, that is 8 weeks If the cost for path 1 -2 and path 2 -3 is the same then We can random pick them to crash so that its completion Time is 8 weeks 9 8 -9

Example – crashing (1) Solution: 4(0) 5 (1) 3 1 OR 8(0) 5 (1) 1 2 4(1) 6(3) 2 3(0) 6(3) 3 8(0) Now, paths 1 -2 -3 and 1 -3 are both critical paths 10 8 -10

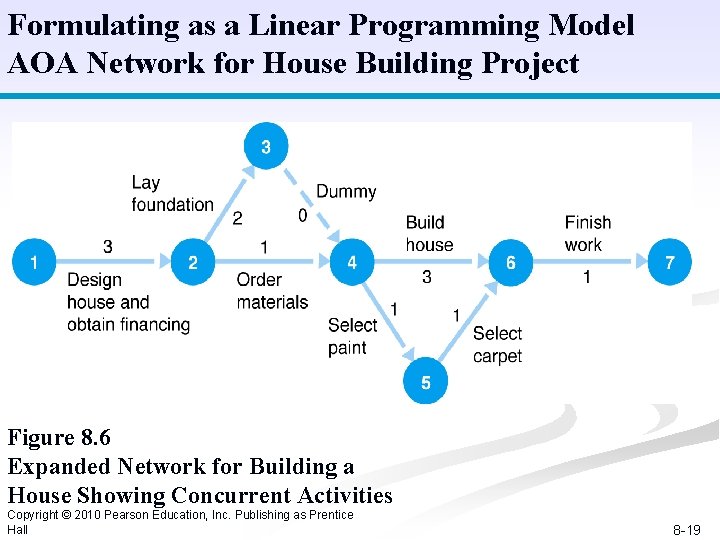
The Project Network AOA Network for House Building Project Figure 8. 6 Expanded Network for Building a House Showing Concurrent Activities Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 8 -11

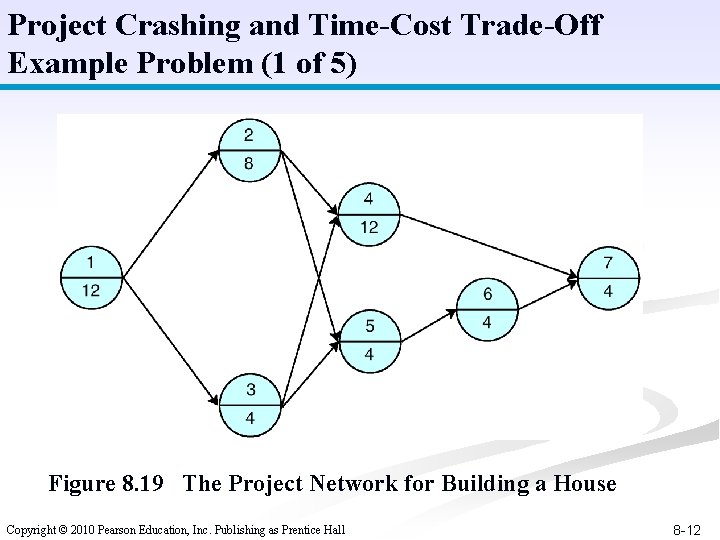
Project Crashing and Time-Cost Trade-Off Example Problem (1 of 5) Figure 8. 19 The Project Network for Building a House Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 8 -12

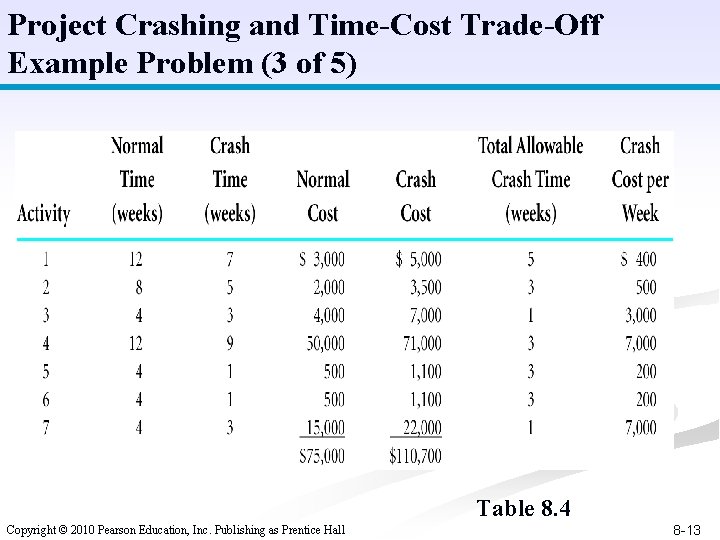
Project Crashing and Time-Cost Trade-Off Example Problem (3 of 5) Table 8. 4 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 8 -13

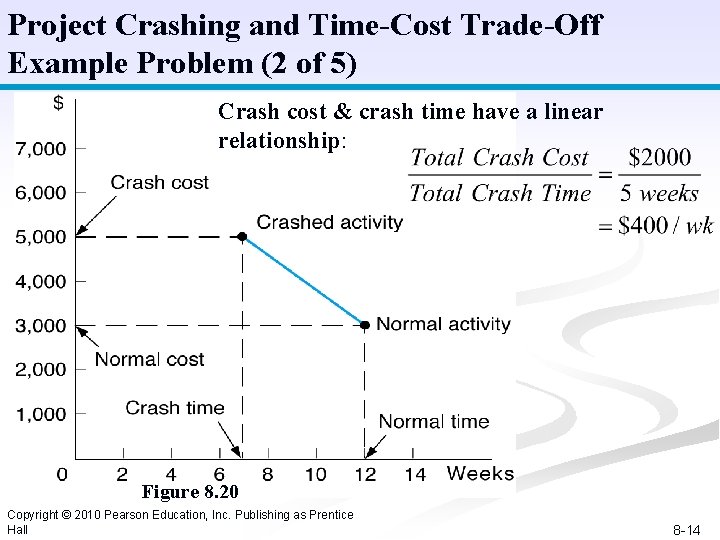
Project Crashing and Time-Cost Trade-Off Example Problem (2 of 5) Crash cost & crash time have a linear relationship: Figure 8. 20 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 8 -14

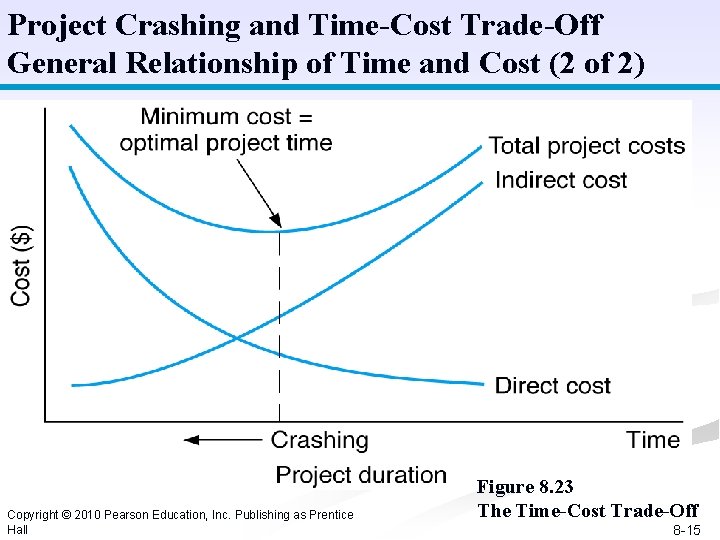
Project Crashing and Time-Cost Trade-Off General Relationship of Time and Cost (2 of 2) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Figure 8. 23 The Time-Cost Trade-Off 8 -15

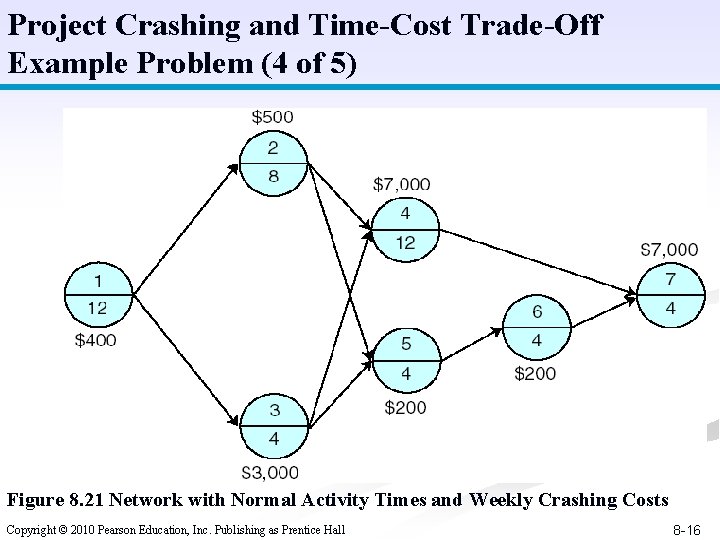
Project Crashing and Time-Cost Trade-Off Example Problem (4 of 5) Figure 8. 21 Network with Normal Activity Times and Weekly Crashing Costs Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 8 -16

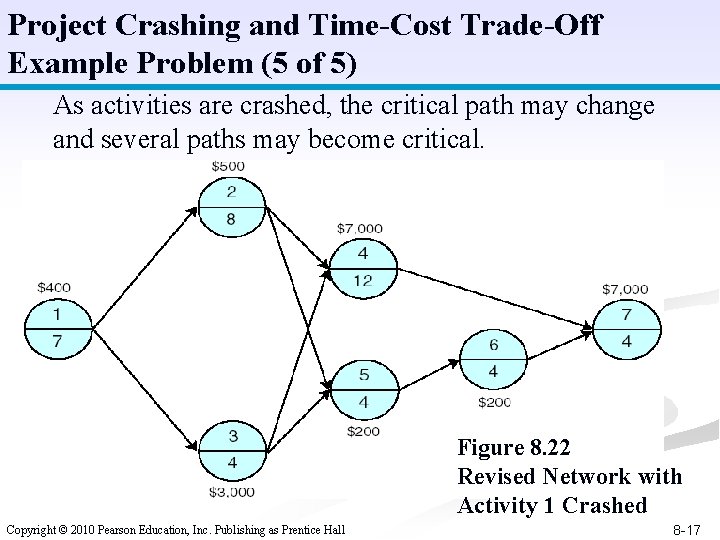
Project Crashing and Time-Cost Trade-Off Example Problem (5 of 5) As activities are crashed, the critical path may change and several paths may become critical. Figure 8. 22 Revised Network with Activity 1 Crashed Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 8 -17

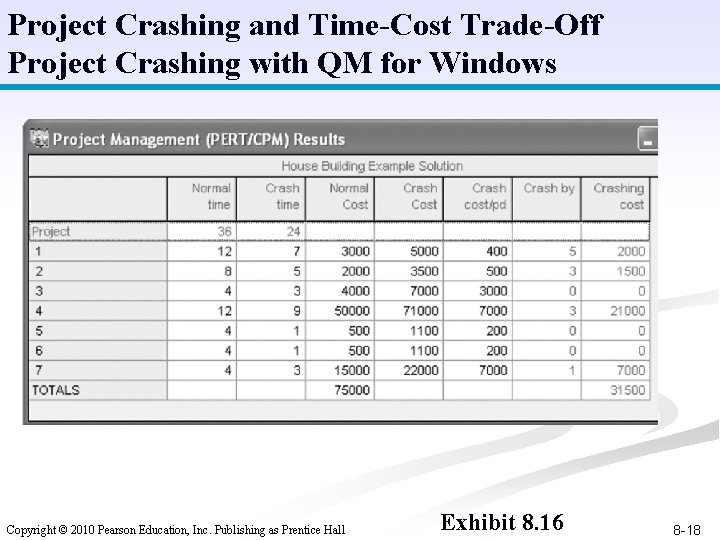
Project Crashing and Time-Cost Trade-Off Project Crashing with QM for Windows Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 8. 16 8 -18

Formulating as a Linear Programming Model AOA Network for House Building Project Figure 8. 6 Expanded Network for Building a House Showing Concurrent Activities Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 8 -19

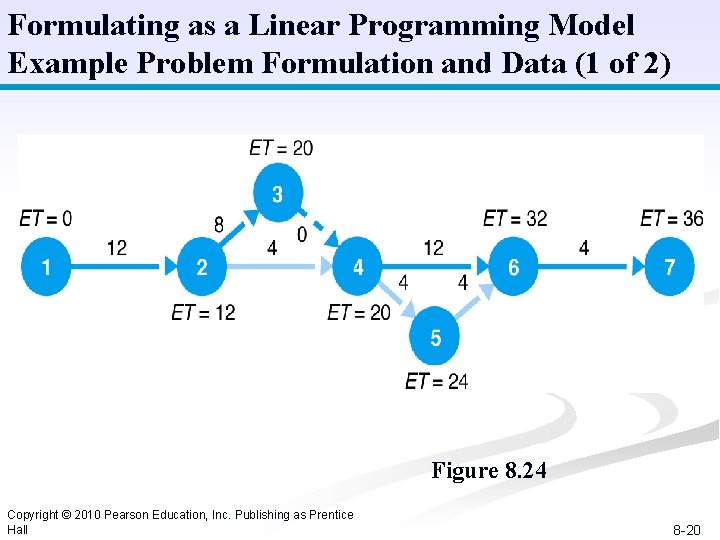
Formulating as a Linear Programming Model Example Problem Formulation and Data (1 of 2) Figure 8. 24 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 8 -20

The CPM/PERT Network Example Problem Formulation and Data (2 of 2) Minimize Z = x 1 + x 2 + x 3 + x 4 + x 5 + x 6 + x 7 subject to: x 2 - x 1 12 x 3 - x 2 8 x 4 - x 2 4 x 4 - x 3 0 x 5 - x 4 4 x 6 - x 4 12 x 6 - x 5 4 x 7 - x 6 4 xi, xj 0 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 8 -21

The CPM/PERT Network Formulating as a Linear Programming Model The objective is to minimize the project duration (critical path time). General linear programming model with AOA convention: Minimize Z = xi subject to: i xj - xi tij for all activities i j xi, xj 0 Where: xi = earliest event time of node i xj = earliest event time of node j tij = time of activity i j Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 8 -22

Project Crashing with Linear Programming Example Problem – Model Formulation Minimize Z = $400 y 12 + 500 y 23 + 3000 y 24 + 200 y 45 + 7000 y 46 + 200 y 56 + 7000 y 67 subject to: y 12 5 y 12 + x 2 - x 1 12 x 7 30 y 23 3 y 23 + x 3 - x 2 8 xi, yij ≥ 0 y 24 1 y 24 + x 4 - x 2 4 Objective is to y 34 0 y 34 + x 4 - x 3 0 minimize the y 45 3 y 45 + x 5 - x 4 4 cost of crashing y 46 3 y 46 + x 6 - x 4 12 y 56 3 y 56 + x 6 - x 5 4 y 67 1 x 67 + x 7 - x 6 4 xi = earliest event time of node i xj = earliest event time of node j yij = amount of time by which activity i j is crashed Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 8 -23