Project Management CHAPTER 3 Outline Learning Objectives What

Project Management CHAPTER 3

Outline Learning Objectives What Is Project Management? Project Charter (宗旨) and Roles Phases of a Project Planning Tool: Work Breakdown Structure Scheduling and Control Tools Gantt Chart PERT and CPM Time/Cost Trade-Offs Evaluating PERT/CPM Why Projects Fail © Springer Publishing Company, LLC. All Rights Reserved. Copyright 3. 2

Learning Objectives Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 3

After reading the chapter, you will be able to: Define the scope of projects Describe a project charter Define the roles and responsibilities of individuals involved in projects Identify the various phases of project management Develop work breakdown structures Draw network diagrams Schedule projects with deterministic times Schedule projects with probabilistic times Crash activity times Discuss the advantages and disadvantages of PERT/CPM Understand the major causes of project failure Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 4

What is Project Management? Copyright © Springer Publishing Company, LLC. All Rights Reserved. DEFINITION

Definition and Constraints Project Management A systematic approach to planning and steering the project processes to achieve specific project goals Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 6

Definition and Constraints Project Management The Triple Constraint Projects must: be within cost be delivered on time meet specifications (quality, scope, standards) Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 6

DEFINITION AND CONTENT PROJECT MANAGER Project Charter and Roles PROJECT TEAM EMPLOYEES IN FUNCTIONAL AREAS EXECUTIVES PROJECT CHAMPIONS Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 7

Definition and Content Roadmap for the project drafted by a project leader includes: A business case A problem statement A goal statement The project scope A list of team members and their roles Milestones and deliverables Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 8

Project Manager ► Directs, supervises, and controls the project from beginning to end Should not carry out project tasks Ensures that all stakeholders are kept informed, conflict is managed, and all issues are addressed Must be able to adapt to and manage change Must maintain good relationships with: Project team members Heads of functional areas Senior management External stakeholders Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 9

Project Team ► Temporary organizational structure designed to harness expertise from many groups throughout the organization ► Defines scope and objectives of project ► Executes tasks and produces deliverables outlined in project plan ► Constructive individuals; consensus builders Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 10

Employees in Functional Areas ► Work must be done by employees in specific functional areas ► Secure the support of the employees’ supervisor ► Ensure good lines of communication are maintained with the functional areas Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 11

Executives ► Guide the project forward, secure the needed resources, and resolve conflicts ► Must make effective and timely project decisions ► Should not lead projects ► Should remain at a distance during the execution unless needed, so as to not stifle the team’s ability to have honest discussions Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 12

Project Champions ► Proclaims the benefits of the project ► Often develops idea for project and can gain support for the project more easily ► Works with different stakeholder groups so that everyone understands why the project is important for the organization Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 13

DEFINITION Phases of a Project PLANNING EXECUTION CONTROL CLOSURE Copyright © Springer Publishing Company,

Definition Phase Project goals are defined and objectives are delineated Critical success factors are explicitly described Everything that needs to happen before the project begins is outlined Stakeholders for the project are identified A project team, with the necessary expertise, is assigned All foreseeable barriers to the project are identified and understood Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 15

Planning Phase Begins with understanding of the underlying objective and the assumptions made Involves operational issues Establishing budgets Setting timelines with major milestones Making decisions regarding personnel involvement and resource allocations Setting performance expectations Project plan communicates to all concerned parties what is going to happen and when Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 16

Execution Phase Involves doing the work to deliver the product or desired outcome Avoid • “scope creep” or “goal shifting” If this happens, the next phases of the project plan will need to be reworked Effective communication is crucial Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 17

Control Phase Focused on systematic monitoring to ensure that the project stays on track Responsibilities • Troubleshoot if problems occur • Hold individuals accountable for their actions • Determine schedule, technical performance, and cost variances Measuring and communicating progress makes team members focus more on results Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 18

Closure Phase End of project; team is disbanded Time to reflect and learn from what happened in the project Were the goals achieved within the “Triple Constraint”? Incorporating a process of intentional and disciplined project review will improve future results Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 19

Planning Tool Copyright © Springer Publishing Company, LLC. All Rights Reserved. WORK BREAKDOWN STRUCTURE

Work Breakdown Structure A hierarchical organization of a project’s components at various levels of detail Helps the planner identify all work requirements of a project and organize them in a logical fashion Steps: 1. Identify the main modules of the project (Level 2) 2. Modules are divided into major activities that need to be carried out to finish the module (Level 3) 3. Major activities are subdivided into activities required to complete them (Level 4) Further breakdowns at higher levels of detail can also be performed if deemed necessary Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 21

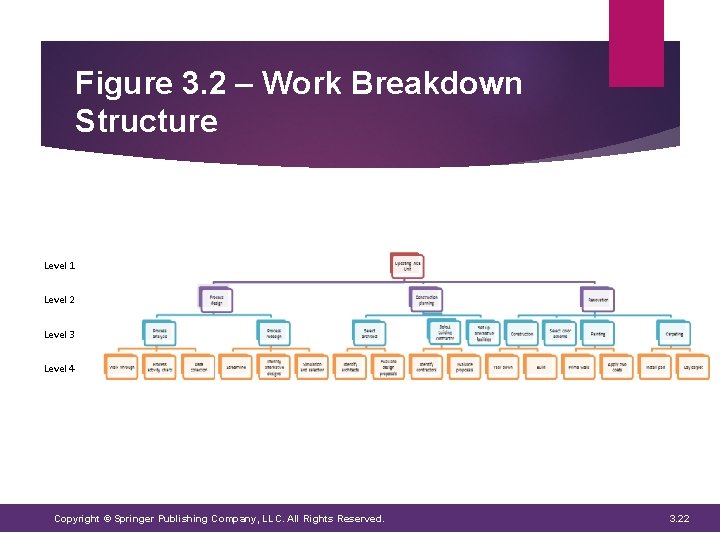
Figure 3. 2 – Work Breakdown Structure Level 1 Level 2 Level 3 Level

Scheduling and Control Tools Copyright © Springer Publishing Company, LLC. All Rights Reserved. GANTT

Gantt Chart A horizontal bar graph Each bar corresponds to a specific activity and its length indicates the duration of the activity Displays information on: the activities to be performed the order in which they must be performed their expected durations the estimated date of project completion Helps monitor the progress of each activity by comparing planned progress to actual progress Appropriate for displaying simple projects with a relatively small number of activities Limited ability to capture interrelationships in more complex projects Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 24

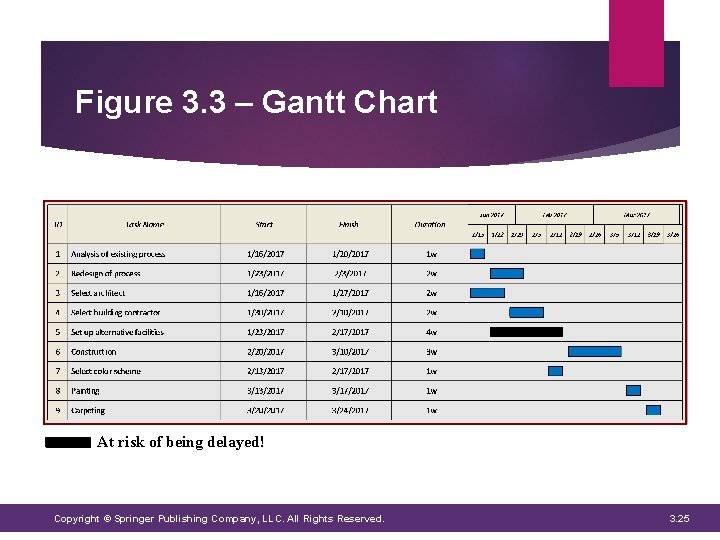
Figure 3. 3 – Gantt Chart At risk of being delayed! Copyright © Springer

PERT and CPM Program Evaluation and Review Technique (PERT) Critical Path Method (CPM) Used together, they provide: A graphic display of all activities and their interrelationships An activity schedule An estimate of the duration of the project A list of the activities critical to the timely completion of the project An estimate of the time by which an activity can be delayed without delaying the entire project (非要徑作業之閒裕時間) Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 26

Network Diagram A graphic display that depicts the project activities and their precedence relationships Two conventions can be utilized: Activity-on the-arrow (AOA) 1. • Arrows = activities • Nodes = beginning and end points Activity-on the-node (AON) 2. • Nodes = activities • Nodes connected by arrows In AOA networks, dummy activities clarify the nature of relationships between activities Consume no time or resources Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 27

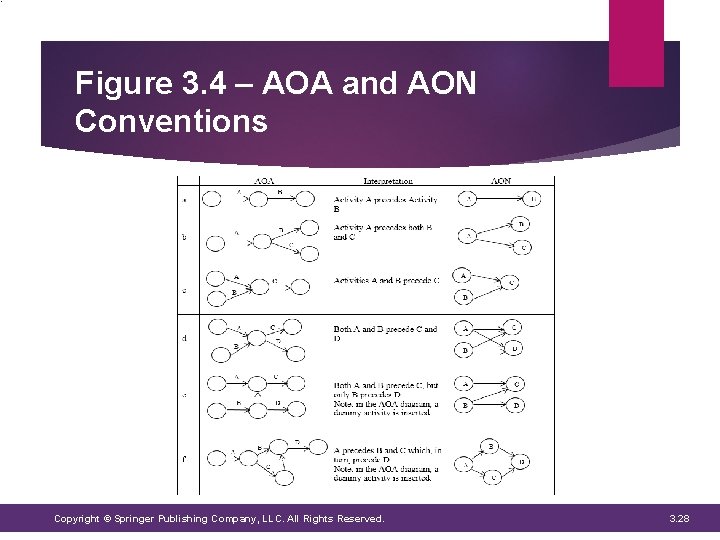
Figure 3. 4 – AOA and AON Conventions Copyright © Springer Publishing Company, LLC.

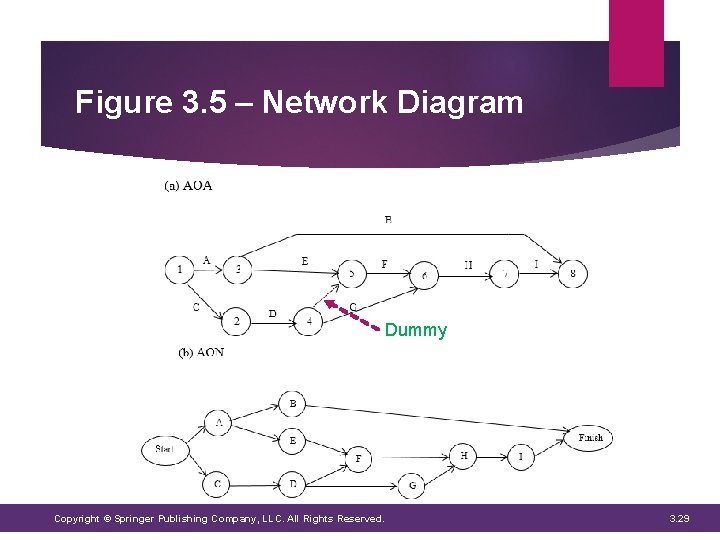
Figure 3. 5 – Network Diagram Dummy Copyright © Springer Publishing Company, LLC. All

Definitions Path Sequence of activities from the starting node to the ending node Duration is determined by summing the expected times of the activities on the path Critical Path Longest path which is critical to on-time project completion Critical activities are the activities along the critical path Shorter paths can experience some delays and not affect the ontime completion of the project as long as their final completion times do not exceed that of the critical path Slack Amount of time by which an activity can be delayed without delaying the entire project Critical activities have no slack since they cannot be delayed Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 30

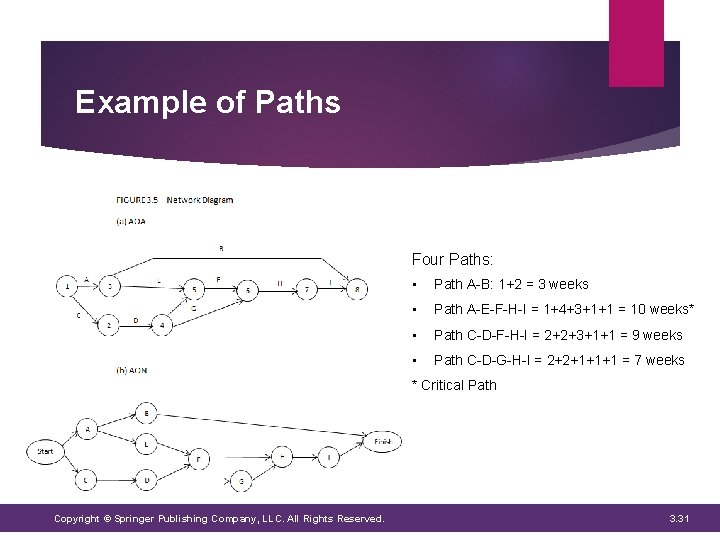
Example of Paths Four Paths: • Path A-B: 1+2 = 3 weeks • Path A-E-F-H-I = 1+4+3+1+1 = 10 weeks* • Path C-D-F-H-I = 2+2+3+1+1 = 9 weeks • Path C-D-G-H-I = 2+2+1+1+1 = 7 weeks * Critical Path Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 31

CPM Method Forward Pass Scheduling of activities from the Start node to the Finish node Requires the computations of the earliest start (ES) and earliest finish (EF) times of each activity on the network Earliest Start (ES) • Earliest time an activity can start if all preceding activities have started at their earliest possible time • ES = maximum (EF times of all immediate predecessors) Earliest Finish (EF) • Earliest time an activity can finish • EF = ES + activity time Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 32

CPM Method (cont. ) Forward Pass ES times: • If an activity has no immediate predecessor, its ES is 0. • If it has one immediate predecessor, its ES is equal to the EF of its predecessor. • If it has multiple immediate predecessors, its ES is equal to the largest of the EF times of its predecessors Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 33

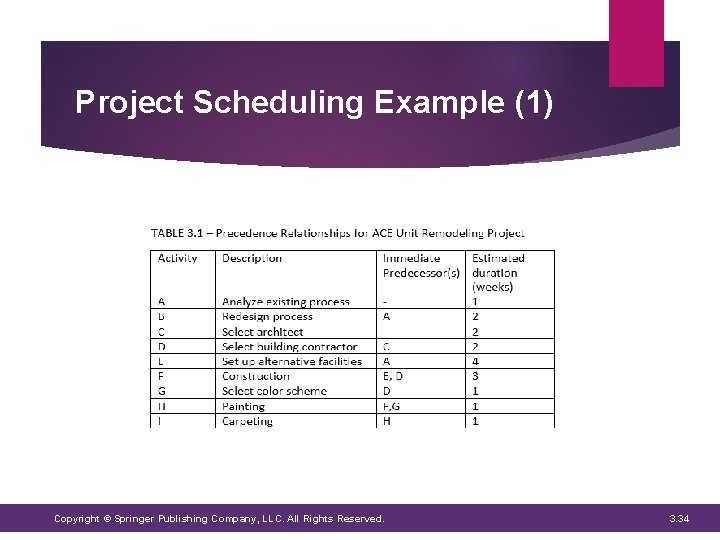
Project Scheduling Example (1) Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3.

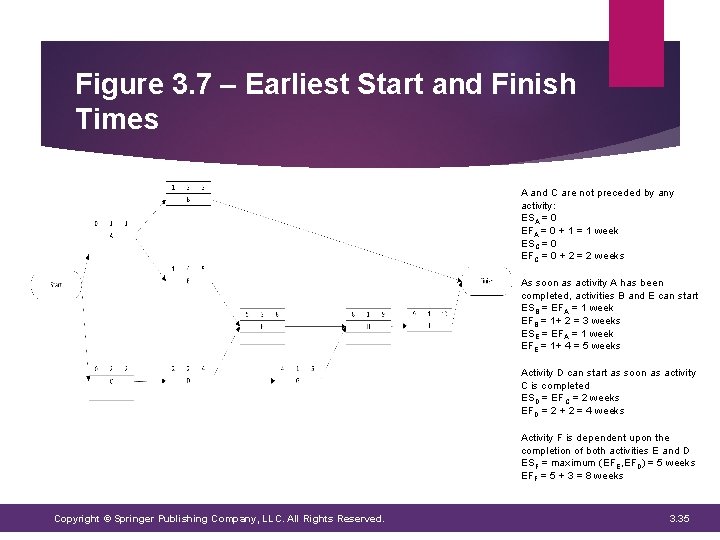
Figure 3. 7 – Earliest Start and Finish Times A and C are not preceded by any activity: ESA = 0 EFA = 0 + 1 = 1 week ESC = 0 EFC = 0 + 2 = 2 weeks As soon as activity A has been completed, activities B and E can start ESB = EFA = 1 week EFB = 1+ 2 = 3 weeks ESE = EFA = 1 week EFE = 1+ 4 = 5 weeks Activity D can start as soon as activity C is completed ESD = EFC = 2 weeks EFD = 2 + 2 = 4 weeks Activity F is dependent upon the completion of both activities E and D ESF = maximum (EFE, EFD) = 5 weeks EFF = 5 + 3 = 8 weeks Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 35

CPM Method (cont. ) Backward Pass Scheduling of activities from the Finish node to the Start node Requires the computations of latest finish (LF) and latest start (LS) times LF = latest time at which an activity can finish without delaying the project • LF = minimum (LS of all immediate followers) LS = latest time at which an activity can start without delaying the project • LS = LF – activity time Because we go “backwards, ” the LF time of an activity is computed before its LS time Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 36

CPM Method (cont. ) LF Times: • If an activity has no immediate follower on the network, its LF is equal to the expected project completion time • If an activity has one immediate follower, its LF is equal to the LS of its follower • If an activity has multiple immediate followers, its LF is equal to the smallest of the LS times of all its followers Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 37

CPM Method (cont. ) Computing Slack (作業的閒裕時間) Based on the numbers computed in the forward pass and in the backward pass: • S = LF – EF OR • S = LS – ES Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 38

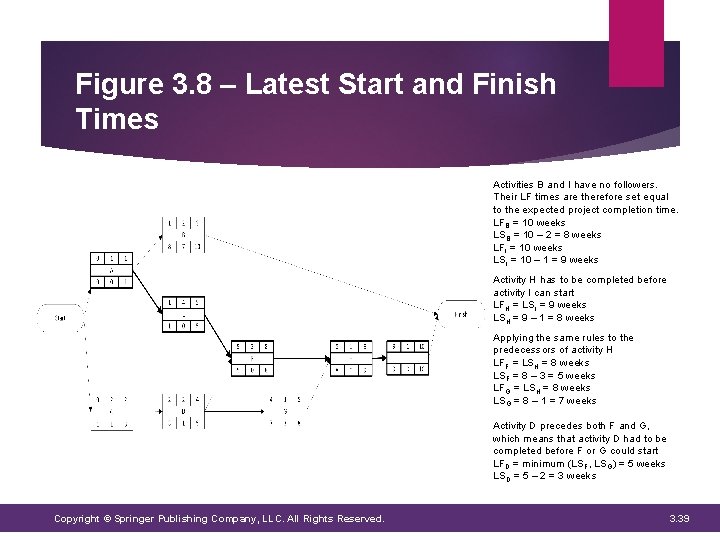
Figure 3. 8 – Latest Start and Finish Times Activities B and I have no followers. Their LF times are therefore set equal to the expected project completion time. LFB = 10 weeks LSB = 10 – 2 = 8 weeks LFI = 10 weeks LSI = 10 – 1 = 9 weeks Activity H has to be completed before activity I can start LFH = LSI = 9 weeks LSH = 9 – 1 = 8 weeks Applying the same rules to the predecessors of activity H LFF = LSH = 8 weeks LSF = 8 – 3 = 5 weeks LFG = LSH = 8 weeks LSG = 8 – 1 = 7 weeks Activity D precedes both F and G, which means that activity D had to be completed before F or G could start LFD = minimum (LSF, LSG) = 5 weeks LSD = 5 – 2 = 3 weeks Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 39

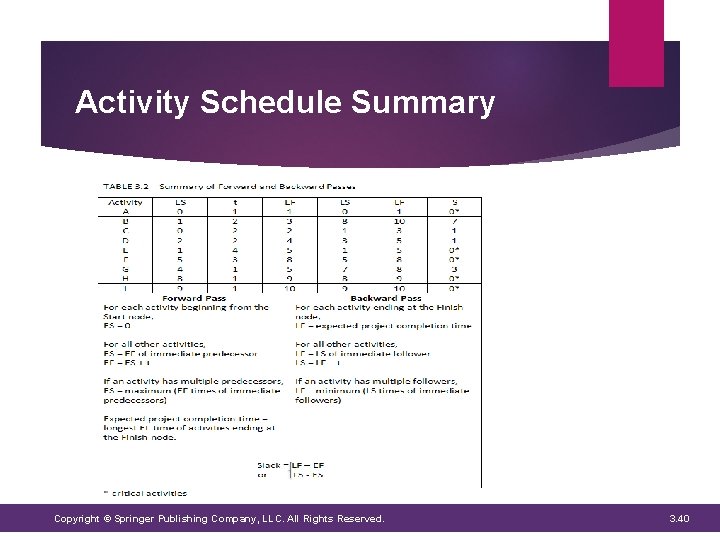
Activity Schedule Summary Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 40

TIME ESTIMATES Probabilistic Times Copyright © Springer Publishing Company, LLC. All Rights Reserved. BETA

Probabilistic Time Estimates Three Time Estimates Optimistic Time (a) time required to perform the activity under ideal conditions • shortest estimated duration for the activity Pessimistic Time (b) • • time required to perform the activity under the worst possible conditions • longest estimated duration for the activity Most Likely Time (m) • most probable time required to execute the activity • lies somewhere between the optimistic and pessimistic time estimates Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 42

Probabilistic Time Estimates (cont. ) Traditional approach to estimating time involves averaging optimistic, pessimistic, and likely conditions te = (a + 4 m + b)/6 • Weighted average • Optimistic (a) and Pessimistic (b) have weight of 1 • Most likely (m) has weight of 4 Variation between a and b spans 6 standard deviations Standard deviation of activity’s time: Variance of the activity’s time: Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 43

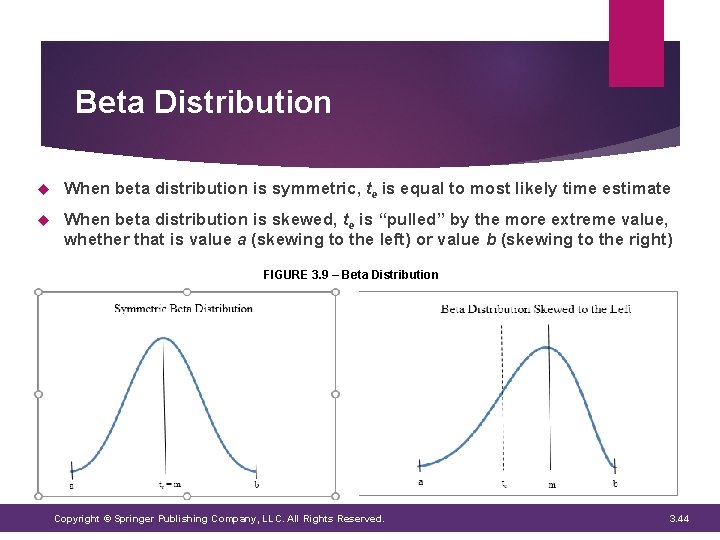
Beta Distribution When beta distribution is symmetric, te is equal to most likely time estimate When beta distribution is skewed, te is “pulled” by the more extreme value, whether that is value a (skewing to the left) or value b (skewing to the right) FIGURE 3. 9 – Beta Distribution Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 44

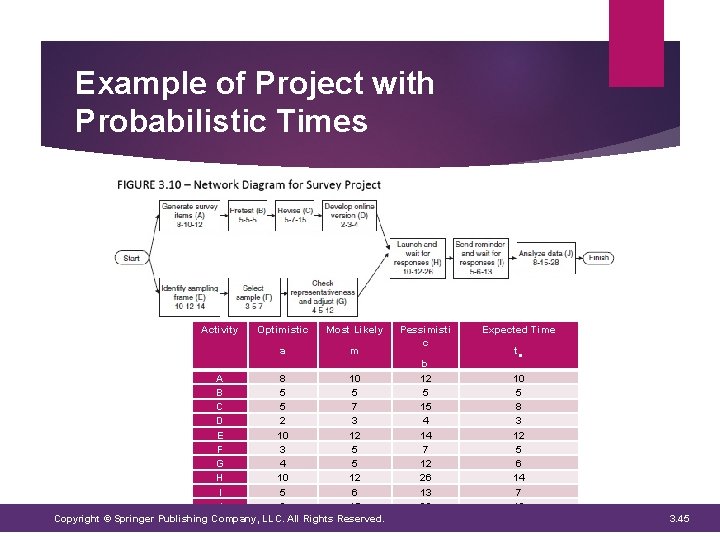
Example of Project with Probabilistic Times Activity Optimistic Most Likely a m A 8 10 B 5 5 C 5 7 D 2 3 E 10 12 F 3 5 G 4 5 H 10 12 I 5 6 J 8 15 Copyright © Springer Publishing Company, LLC. All Rights Reserved. Pessimisti c b 12 5 15 4 14 7 12 26 13 28 Expected Time te 10 5 8 3 12 5 6 14 7 16 3. 45

Path Variation To measure the project’s variability, PERT utilizes the standard deviation of the

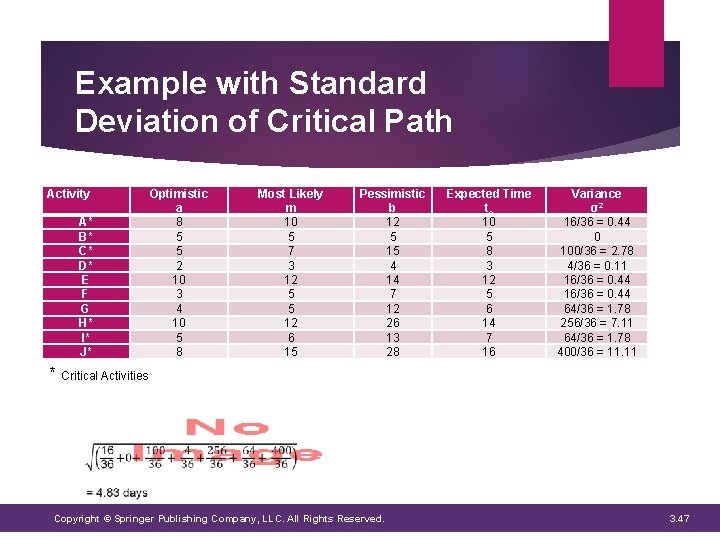
Example with Standard Deviation of Critical Path Activity A* B* C* D* E F G H* I* J* Optimistic a 8 5 5 2 10 3 4 10 5 8 Most Likely m 10 5 7 3 12 5 5 12 6 15 Pessimistic b 12 5 15 4 14 7 12 26 13 28 Expected Time te 10 5 8 3 12 5 6 14 7 16 Variance σ2 16/36 = 0. 44 0 100/36 = 2. 78 4/36 = 0. 11 16/36 = 0. 44 64/36 = 1. 78 256/36 = 7. 11 64/36 = 1. 78 400/36 = 11. 11 * Critical Activities Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 47

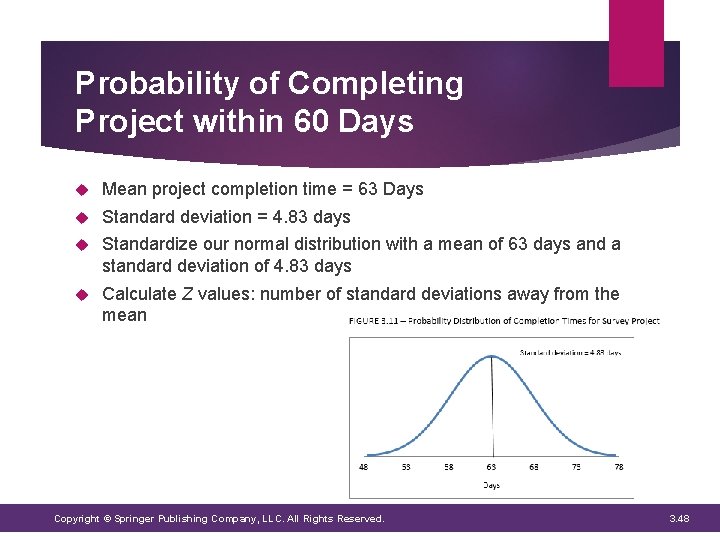
Probability of Completing Project within 60 Days Mean project completion time = 63 Days Standard deviation = 4. 83 days Standardize our normal distribution with a mean of 63 days and a standard deviation of 4. 83 days Calculate Z values: number of standard deviations away from the mean Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 48

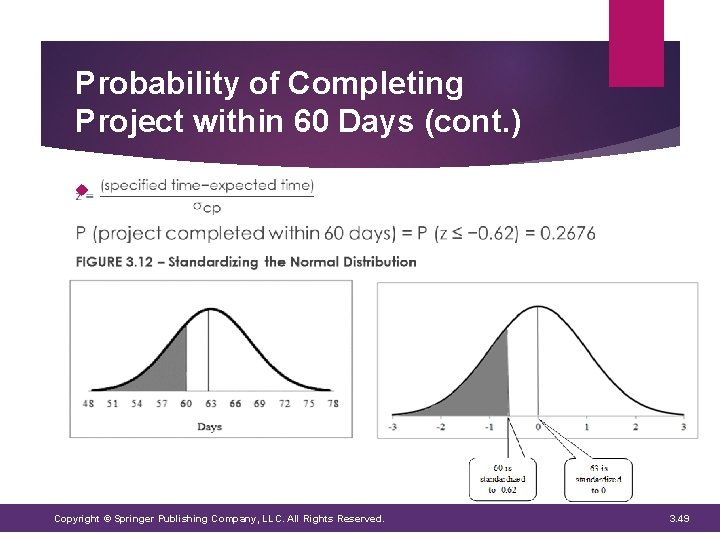
Probability of Completing Project within 60 Days (cont. ) Copyright © Springer Publishing Company,

Time/Cost Trade-Offs Copyright © Springer Publishing Company, LLC. All Rights Reserved. CRASH TIMES AND

Time/Cost Trade-Offs Two of a project’s constraints are time and cost Activities along the critical path are “crashed” to shorten their durations BUT doing so requires the use of more personnel, subcontractors, equipment, etc. which adds to the cost of the project Need to obtain estimates of the potential time reductions for each activity and of the extra costs involved tn: the normal time to complete an activity. This is the time it takes to perform an activity with a normal amount of resources. tc: the crash time to complete an activity. This is the shortest amount of time it takes to perform an activity when maximum resources are expended. cn: the normal cost to complete an activity. This the cost associated with the completion of the activity within its normal time. cc: the crash cost to complete the activity. This is the cost associated with performing the activity within its crash time. Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 51

Time/Cost Trade-Offs (cont. ) Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3.

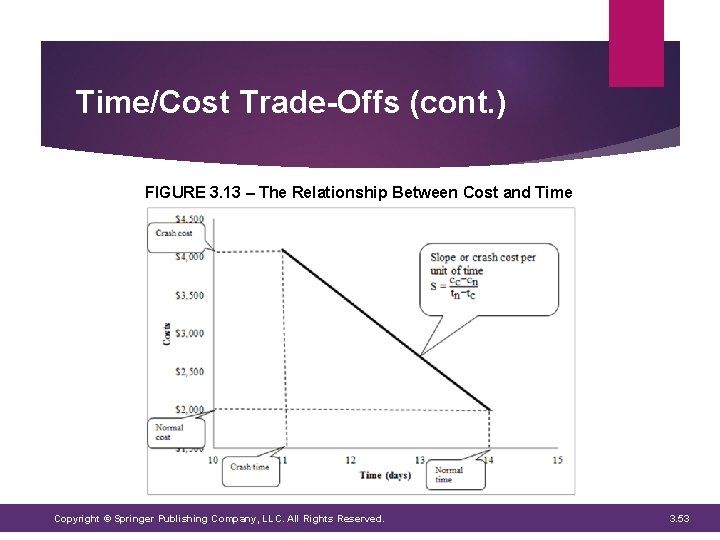
Time/Cost Trade-Offs (cont. ) FIGURE 3. 13 – The Relationship Between Cost and Time

Marginal Cost Analysis Involves crashing activities along the critical path in such a way that incremental costs are minimized This crashing procedure comprises five steps: STEP 1: Compute t. RED and S for each activity STEP 2: Identify all the paths and their respective durations STEP 3: Find the cheapest critical activity to crash and reduce its duration by the maximum time allowable without overlooking another critical path (i. e. , a path that was originally shorter might become as long as the crashed critical path). STEP 4: If one or more other critical paths emerge, proceed in a similar fashion by finding the cheapest activities to crash along those paths and sum their crashing costs. If these paths share a common activity, compare the cost of crashing the common activity with the sum of the crashing costs of the least expensive activities to crash on the separate critical paths. STEP 5: Repeat this process until you have reached the desired project completion time. Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 54

Marginal Cost Analysis (cont. ) Example: Crash project to 55 days Step 1: Compute

Marginal Cost Analysis (cont. ) Step 2: Identify all the paths and their respective durations: v A-B-C-D-H-I-J: 63 days * critical path v E-F-G-H-I-J: 60 days Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 56

Marginal Cost Analysis (cont. ) Step 3: Find the cheapest critical activity to crash and reduce its duration by the maximum time allowable without overlooking another critical path • On the critical path, Activity C is the cheapest to crash v Maximum duration = 2 days v $100 x 2 = $200 v Project cost increases from $9, 800 to $10, 000 • Next cheapest activity to crash on that path is Activity A v Crash only by 1 day = $150 v New project cost = $10, 150 • Critical paths: v A-B-C-D-H-I-J: 60 days * critical path v E-F-G-H-I-J: 60 days * critical path Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 57

Marginal Cost Analysis (cont. ) Step 4: Both paths are now critical v On path A-B-C-D-H-I-J crash A for $150/day v On path E-F-G-H-I-J crash G for $150/day TOTAL: $300/day v BUT choose to crash I since cost is only $250/day • A-B-C-D-H-I-J: 59 days * critical path • E-F-G-H-I-J: 59 days * critical path • Project cost is now $10, 400 Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 58

Marginal Cost Analysis (cont. ) Step 5: Crashing additional activities v Crashing H = $700 v Crashing J = $550 • Either cost is higher than that of crashing both A and G (common activities) simultaneously • Crash A and G both by 2 days = $600 • New project cost = $11, 000 • Critical Paths: v A-B-C-D-H-I-J: 57 days * critical path v E-F-G-H-I-J: 57 days * critical path Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 59

Marginal Cost Analysis (cont. ) Step 5: Crashing additional activities • The next cheapest activities to crash are activities D and F v Combined crashing cost for one day is $700 v More expensive than the cost of crashing J, a common activity, for $550 • Crash J by 2 days and reach the target of 55 days • Total cost of the project is now $12, 100 • Critical Paths: v A-B-C-D-H-I-J: 55 days * critical path v E-F-G-H-I-J: 55 days * critical path Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 60

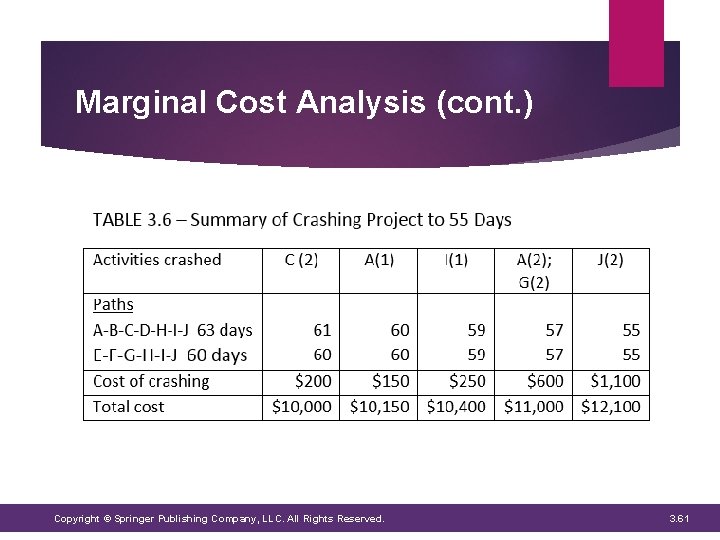
Marginal Cost Analysis (cont. ) Copyright © Springer Publishing Company, LLC. All Rights Reserved.

Linear Programming A decision-making technique that provides an optimal solution given a specific objective and a set of constraints The decision to be made involves which activities to crash and by how much • The objective is to minimize the cost of reducing the project’s duration • The constraints or limitations include: • 1) The amount of time by which each activity can be crashed 2) The amount of time by which each path must be reduced to reach a desired project completion time Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 62

Linear Programming (cont. ) Compute t. RED and S STEP 1: Formulate the decision variables. The decision variables are the key elements of the decision; their values make up the solution. They need to be defined very precisely Xi = number of days by which activity I must be crashed (I = A − J) STEP 2: Formulate the objective function. The objective function expresses the objective of the model, which here is to minimize the cost of crashing Minimize cost = 150 XA + 0 XB + 100 XC + 500 XD + 350 XE + 200 XF + 150 XG + 700 XH + 250 XI + 550 XJ STEP 3: Formulate the constraints. There are two major sets of constraints: 1. those limiting the amount of time by which an activity can be crashed 2. those ensuring that each path is crashed by a sufficient amount of time to achieve the desired project completion time. Additionally, at the end, we need to specify that the decision variables—time reductions—can only take on positive values Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 63

Linear Programming (cont. ) Step 3 (cont. ) First set: XA ≤ 3 XB

Linear Programming (cont. ) Step 3 (cont. ) Second set: XA + XB + XC + XD + XH + X I + X J XE + XF + XG + XH + XI + XJ ≥ 8 ≥ 5 Logical constraint: Xi ≥ 0 (I = A − J) Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 65

Evaluating PERT/CPM Copyright © Springer Publishing Company, LLC. All Rights Reserved. ADVANTAGES DISADVANTAGES 3.

Evaluating PERT/CPM Advantages 1. The technique forces project managers to organize the project information in a logical fashion and quantify it 2. The network diagram provides a graphic display of the project and its activities. It is a common point of reference for all the parties involved in the project 3. The technique is not overly complex and can be learned easily 4. Knowledge of the critical activities enables the project manager to: a) monitor closely the activities whose delay would postpone the completion of the entire project b) potentially allow delays for those activities that have slack. Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 67

Evaluating PERT/CPM (cont. ) Disadvantages 1. It is sometimes impossible to identify all activities, especially for complex projects. Omissions will emerge and may require a substantial modification of the schedule 2. Time estimates are just that: estimates. They tend to be subjective and could be quite inaccurate—fudge factor—for first-time endeavors 3. There is a tendency to focus too much on the critical path and overlook other paths that are near critical or become critical as a result of delays Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 68

Why Projects Fail Copyright © Springer Publishing Company, LLC. All Rights Reserved. MAIN REASONS

Main Reasons Goals are not understood throughout the organization There is a misalignment between the organization’s strategy and the goals of the project Timelines are unrealistic Resources are not available Planning is poor Rigorous project management methodology is not followed Inadequate communication, progress tracking, and reporting Copyright © Springer Publishing Company, LLC. All Rights Reserved. 3. 70