Project Course in Adaptive Signal Processing Acoustic Positioning

Problem statement We want to find the position of a microphone. Measure travel times

Basic principle • Let each speaker transmit a unique “training sequence”. • Correlate the

Impact of training sequences As a first attempt, we try using four different tones:

Impact of training sequences Instead, use wideband binary noise: → much better result!

Finding the position • Express measured distances in terms of z, y, z →

Position tracking • Noise in the range measurements can be suppressed by filtering. You

Problems • Imprecise measurements – EKF probably works well, but additional algorithms for discarding

Problems • The near-far problem – Speakers near the microphone become too dominant. Implement

References • “Atomic Clock Augmentation For Receivers Using the Global Positioning System”, Paul A.

Slides: 10

Download presentation

Project Course in Adaptive Signal Processing Acoustic Positioning Daniel Aronsson

Problem statement We want to find the position of a microphone. Measure travel times from fixed speakers to the microphone. Based on these measurements, calculate x, y, z for the microphone. The speakers’ positions are known. Initially we will use four speakers, but more can be added for improved accuracy.

Basic principle • Let each speaker transmit a unique “training sequence”. • Correlate the recorded signal with each training sequence to find the respective travel times. • Each sequence should be as uncorrelated as possible with – the other sequences – itself for time lags other than zero

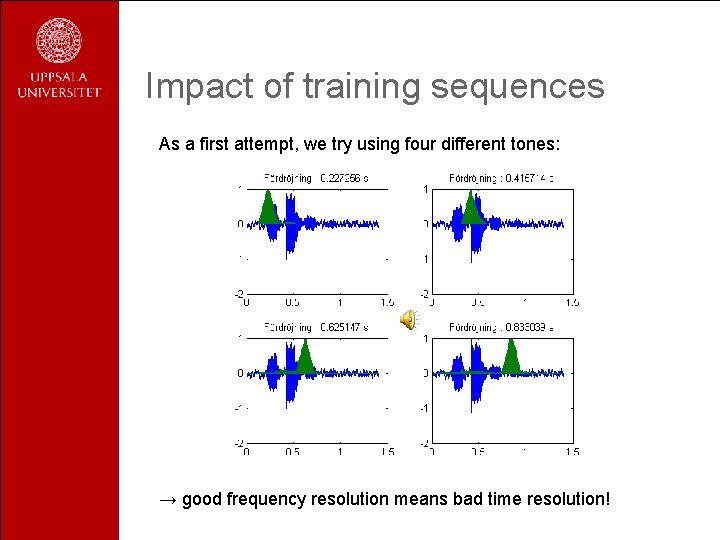
Impact of training sequences As a first attempt, we try using four different tones: → good frequency resolution means bad time resolution!

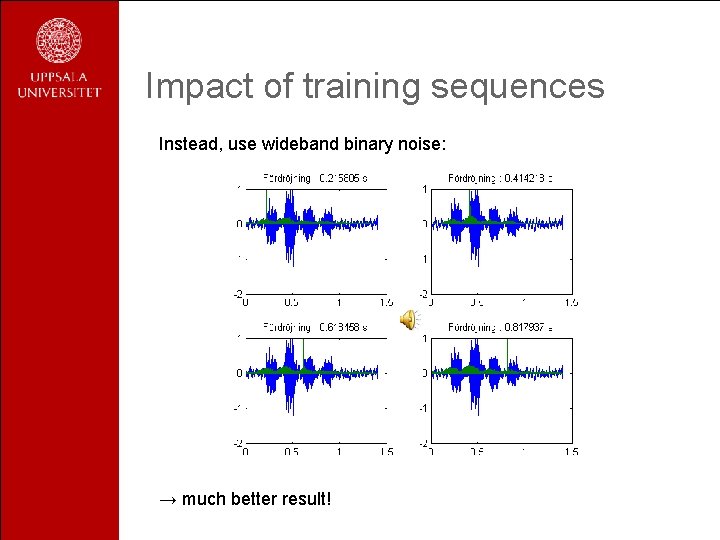
Impact of training sequences Instead, use wideband binary noise: → much better result!

Finding the position • Express measured distances in terms of z, y, z → quadratic equations! • Many solution methods, both numeric and analytic, but the method used need to be robust to imperfect measurements and noise. • In the provided test code, I solve the problem by linearizations and iterations. • Another, and better, idea is to use Extended Kalman Filtering (see next slide)

Position tracking • Noise in the range measurements can be suppressed by filtering. You may e. g. model each range measurement as a random walk plus noise. • A better approach is to use an Extended Kalman Filter (EKF). Let x, y, z, t be the states and linearize the nonlinear measurement equation. Using EKF makes the previous linearization obsolete.

Problems • Imprecise measurements – EKF probably works well, but additional algorithms for discarding bad measurements might be needed. • Potential non-line-of-sight – Use many parallel filter, each measuring a unique subset if ranges, and keep only the best estimate? • Moving microphone – In the present code, the microphone need to be still during measurements. • Reverberation – Measure speaker impulse responses and deconvolute?

Problems • The near-far problem – Speakers near the microphone become too dominant. Implement an algorithm that adjusts the speakers’ volumes (a crude algorithm is already implemented). • Simultaneous training sequences – Training sequences currently need to be transmitted one by one. Implement simultaneous training. • Continuous training?

References • “Atomic Clock Augmentation For Receivers Using the Global Positioning System”, Paul A. Kline, Ph. D dissertation • ” Basics of the GPS Technique: Observation Equations”, Geoffrey Blewitt • “Audio Signal Processing for Next Generation Multimedia Communication Systems”, Yiteng Huang, Jacob Benesty, and Gary W. Elko, Kluwer 2004