Progress on ElectronPositron Linear Colliders and Technology Bob

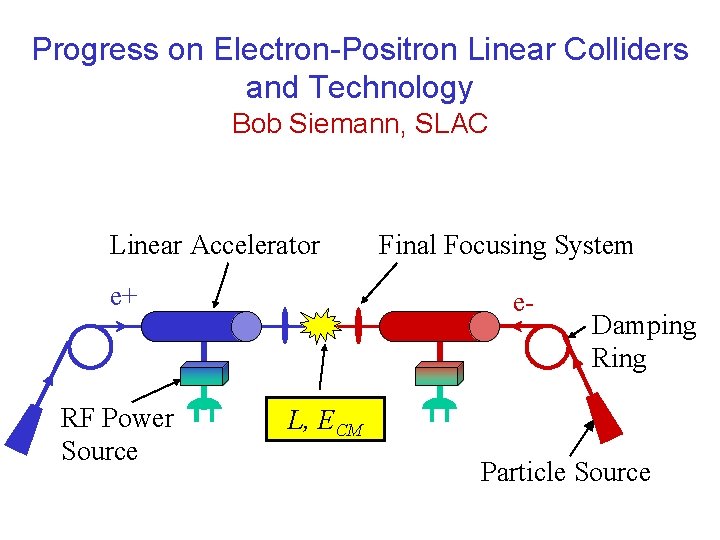
Progress on Electron-Positron Linear Colliders and Technology Bob Siemann, SLAC Linear Accelerator e+ RF Power Source Final Focusing System e- Damping Ring L, ECM Particle Source

Progress on Electron-Positron Linear Colliders and Technology Bob Siemann, SLAC 1. 2. 3. 4. 5. 6. 7. Luminosity and the Beam-Beam Interaction Energy Spread, Emittance & Wakefields Superconducting & Room Temperature Linacs RF Power Damping Rings & Bunch Compressors E+ Production & E- Sources Perspective

PHYSICAL PROCESSES IN THE COLLISON LIMIT THE SINGLE PULSE L N=1010, E = 250 Ge. V, sx = 500 nm, sy = 5 nm, sz = 300 mm • Photon radiation & e+e- pair production Backgrounds and ECM spread • Focusing during the collision Reduction of spot size and increased L

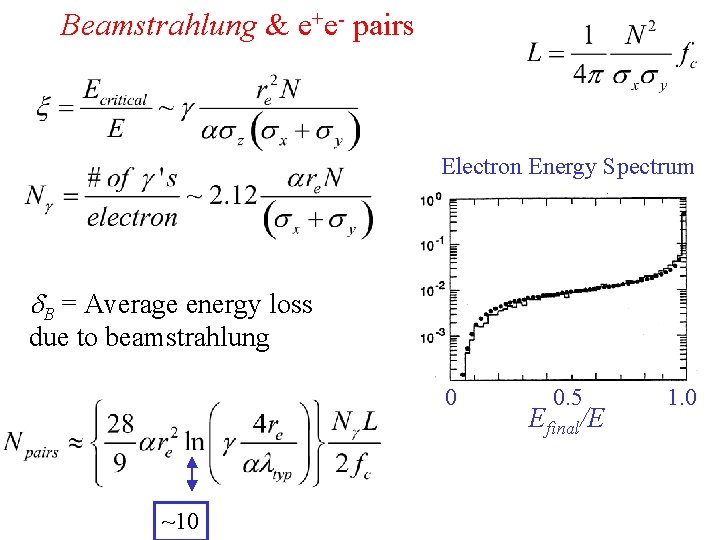
Beamstrahlung & e+e- pairs Electron Energy Spectrum d. B = Average energy loss due to beamstrahlung 0 ~10 0. 5 Efinal/E 1. 0

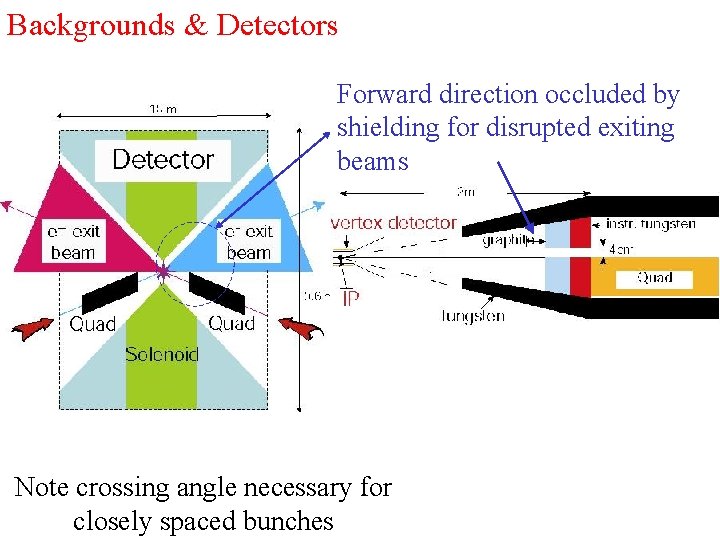
Backgrounds & Detectors Forward direction occluded by shielding for disrupted exiting beams Note crossing angle necessary for closely spaced bunches

Basic Luminosity Scaling Minimize the area while maximizing the perimeter Flat beams sx >> sy

Basic Luminosity Scaling Number of g’s Backgrounds and energy spread Beam power High efficiency to convert AC to beam power Small flat spot with sx >> sy This discussion has ignored focusing during the collision • Called “Disruption” • Substantial increase in luminosity • Affects the EM fields at collision point & radiation, etc

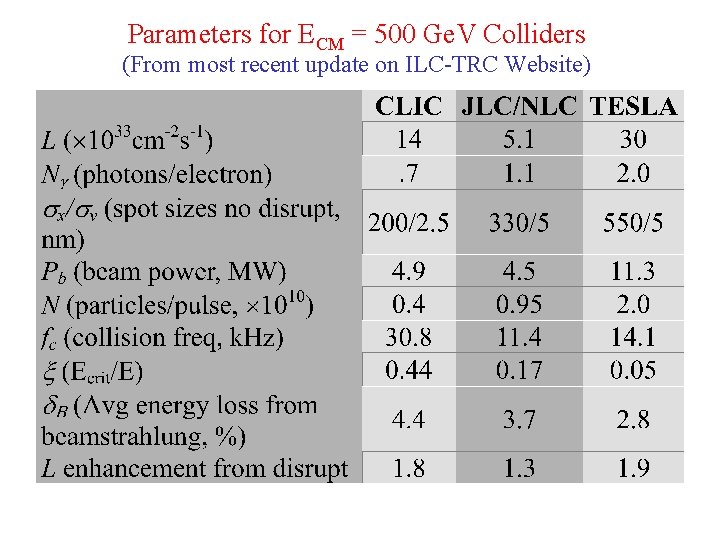
Parameters for ECM = 500 Ge. V Colliders (From most recent update on ILC-TRC Website)

Progress on Electron-Positron Linear Colliders and Technology Bob Siemann, SLAC 1. 2. 3. 4. 5. 6. 7. Luminosity and the Beam-Beam Interaction Energy Spread, Emittance & Wakefields Superconducting & Room Temperature Linacs RF Power Damping Rings & Bunch Compressors E+ Production & E- Sources Perspective

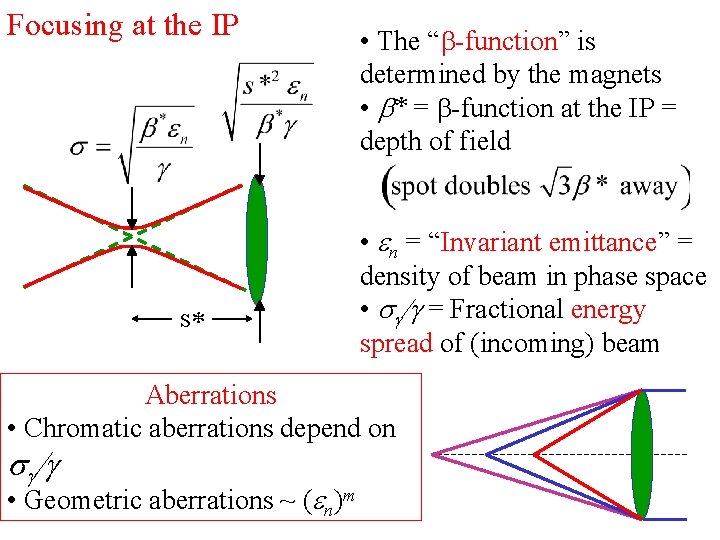
Focusing at the IP s* • The “b-function” is determined by the magnets • b* = b-function at the IP = depth of field • en = “Invariant emittance” = density of beam in phase space • sg/g = Fractional energy spread of (incoming) beam Aberrations • Chromatic aberrations depend on sg/g • Geometric aberrations ~ (en)m

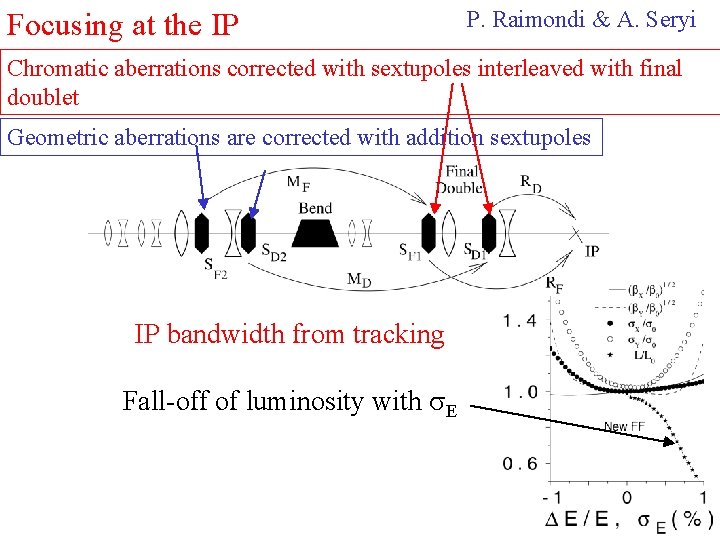
Focusing at the IP P. Raimondi & A. Seryi Chromatic aberrations corrected with sextupoles interleaved with final doublet Geometric aberrations are corrected with addition sextupoles IP bandwidth from tracking Fall-off of luminosity with s. E

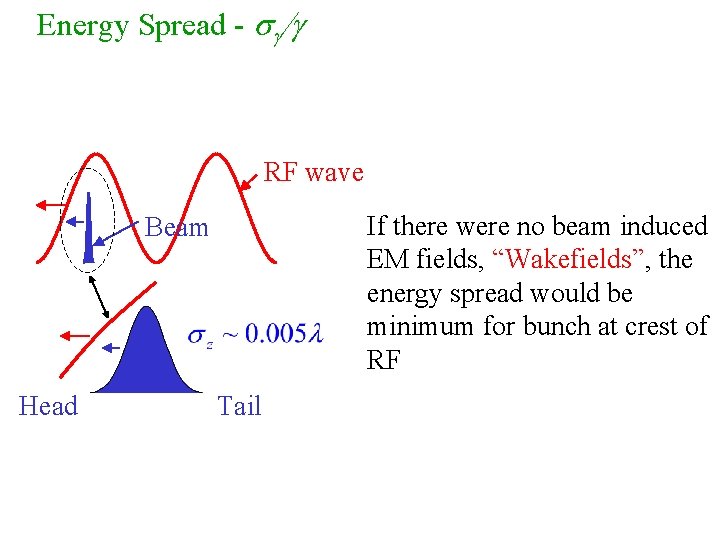
Energy Spread - sg/g RF wave If there were no beam induced EM fields, “Wakefields”, the energy spread would be minimum for bunch at crest of RF Beam Head Tail

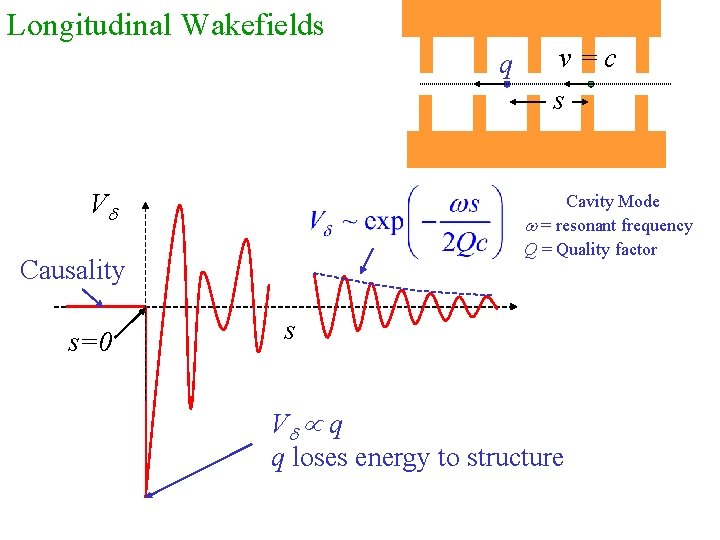
Longitudinal Wakefields q Vd Cavity Mode w = resonant frequency Q = Quality factor Causality s=0 v=c s s Vd q q loses energy to structure

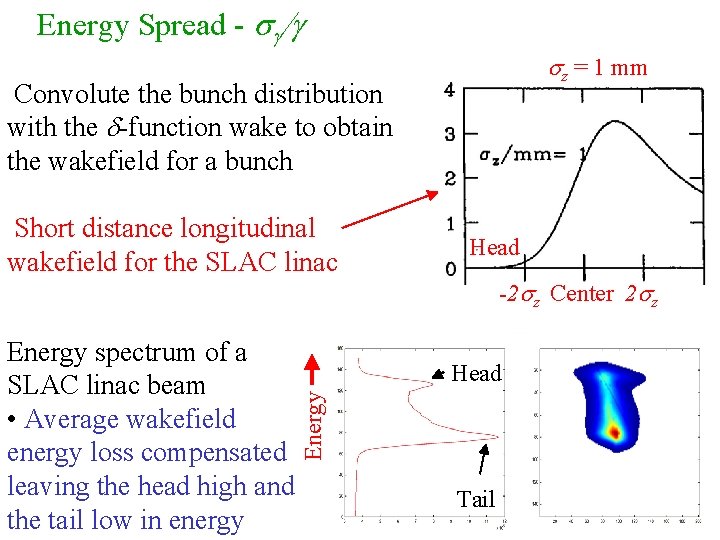
Energy Spread - sg/g sz = 1 mm Convolute the bunch distribution with the d-function wake to obtain the wakefield for a bunch Short distance longitudinal wakefield for the SLAC linac -2 sz Center 2 sz Head Energy spectrum of a SLAC linac beam • Average wakefield energy loss compensated leaving the head high and the tail low in energy Head Tail

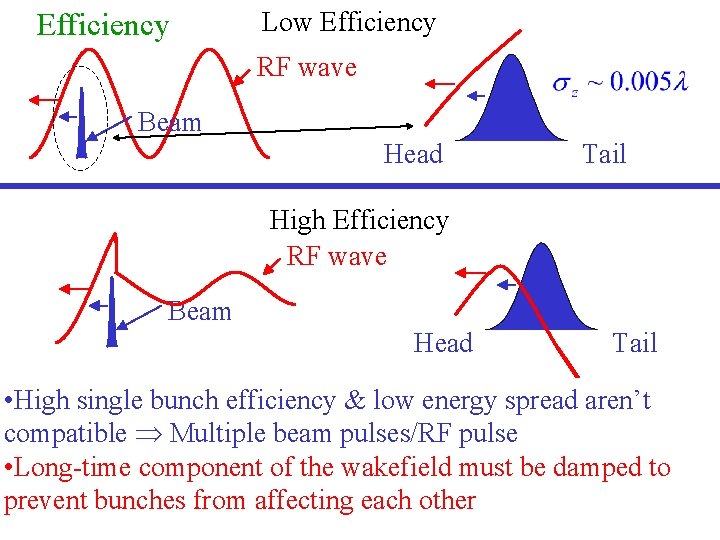
Efficiency Low Efficiency RF wave Beam Head Tail High Efficiency RF wave Beam Head Tail • High single bunch efficiency & low energy spread aren’t compatible Multiple beam pulses/RF pulse • Long-time component of the wakefield must be damped to prevent bunches from affecting each other

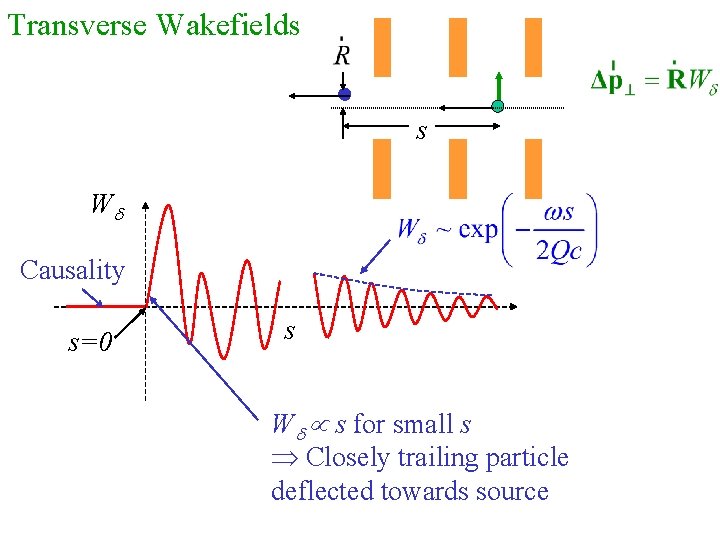
Transverse Wakefields s Wd Causality s=0 s Wd s for small s Closely trailing particle deflected towards source

Emittance: Liouville’s Theorem and RMS Emittance t 2 p Liouville’s Theorem: The phase space (p, q) density is a constant as a Hamiltonian system evolves in time. t 1 q • Phase space area (A) containing a defined number of particles is constant • Accelerator physicists use position and angle: • Invariant emittance (en) is the phase space area • Liouville’s theorem en is constant

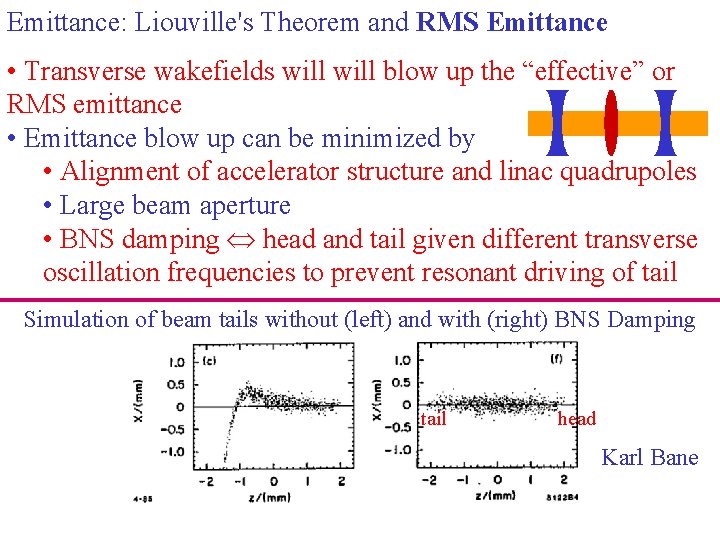
Emittance: Liouville's Theorem and RMS Emittance • Transverse wakefields will blow up the “effective” or RMS emittance • Emittance blow up can be minimized by • Alignment of accelerator structure and linac quadrupoles • Large beam aperture • BNS damping head and tail given different transverse oscillation frequencies to prevent resonant driving of tail Simulation of beam tails without (left) and with (right) BNS Damping tail head Karl Bane

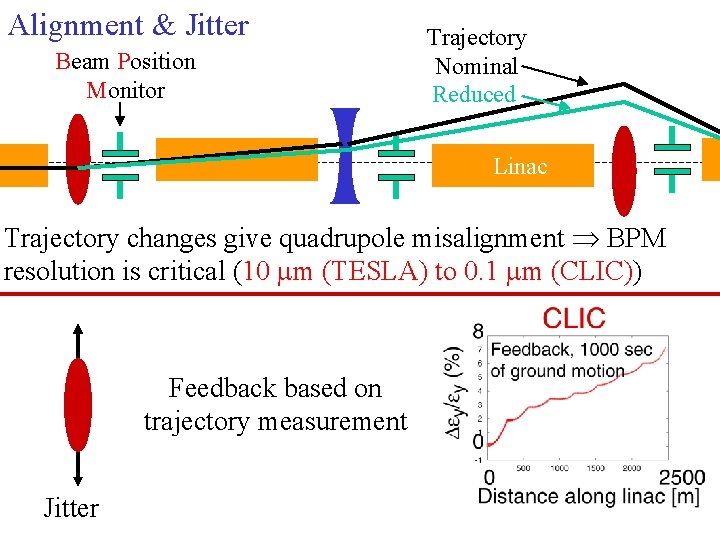
Alignment & Jitter Beam Position Monitor Trajectory Nominal Reduced Linac Trajectory changes give quadrupole misalignment BPM resolution is critical (10 mm (TESLA) to 0. 1 mm (CLIC)) Feedback based on trajectory measurement Jitter

Progress on Electron-Positron Linear Colliders and Technology Bob Siemann, SLAC 1. 2. 3. 4. 5. 6. 7. Luminosity and the Beam-Beam Interaction Energy Spread, Emittance & Wakefields Superconducting & Room Temperature Linacs RF Power Damping Rings & Bunch Compressors E+ Production & E- Sources Perspective

I would like my linac structure to: Have a high accelerating gradient Transfer energy efficiently to particles Have low wakefields

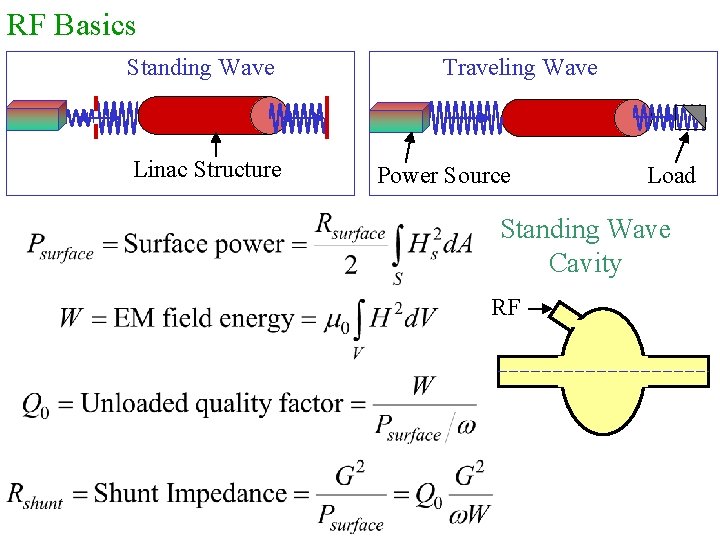
RF Basics Standing Wave Linac Structure Traveling Wave Power Source Load Standing Wave Cavity RF

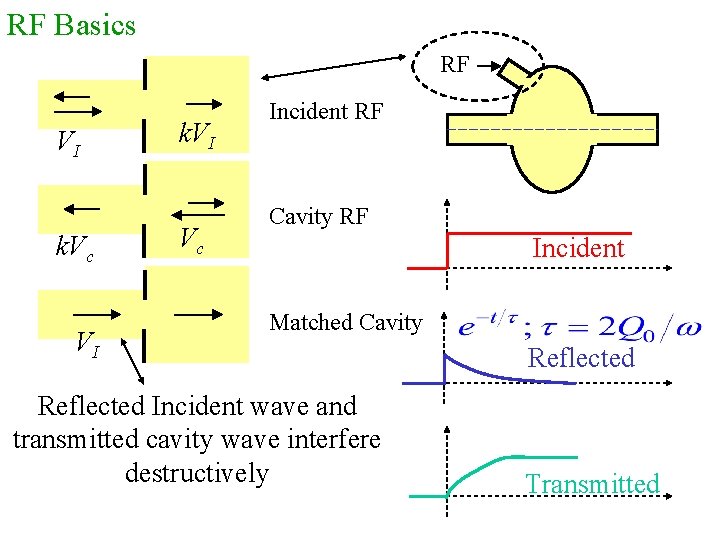
RF Basics RF VI k. Vc VI k. VI Vc Incident RF Cavity RF Incident Matched Cavity Reflected Incident wave and transmitted cavity wave interfere destructively Reflected Transmitted

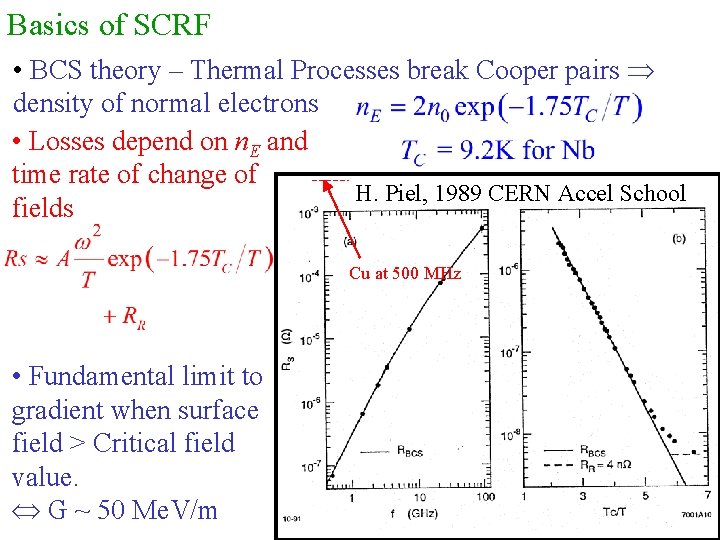
Basics of SCRF • BCS theory – Thermal Processes break Cooper pairs density of normal electrons • Losses depend on n. E and time rate of change of H. Piel, 1989 CERN Accel School fields Cu at 500 MHz • Fundamental limit to gradient when surface field > Critical field value. G ~ 50 Me. V/m

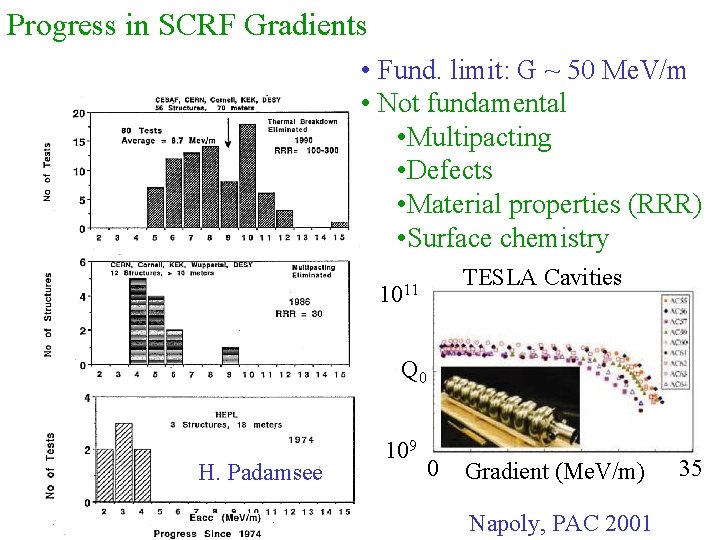
Progress in SCRF Gradients • Fund. limit: G ~ 50 Me. V/m • Not fundamental • Multipacting • Defects • Material properties (RRR) • Surface chemistry TESLA Cavities 1011 Q 0 H. Padamsee 109 0 Gradient (Me. V/m) Napoly, PAC 2001 35

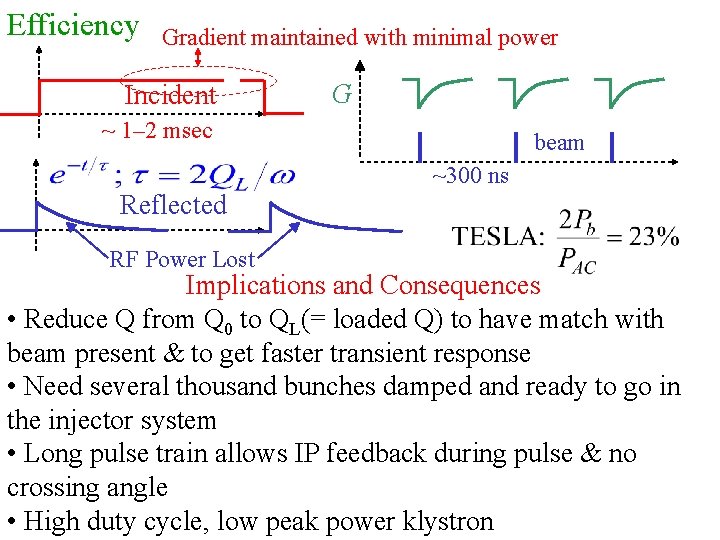
Efficiency Gradient maintained with minimal power Incident G ~ 1– 2 msec beam ~300 ns Reflected RF Power Lost Implications and Consequences • Reduce Q from Q 0 to QL(= loaded Q) to have match with beam present & to get faster transient response • Need several thousand bunches damped and ready to go in the injector system • Long pulse train allows IP feedback during pulse & no crossing angle • High duty cycle, low peak power klystron

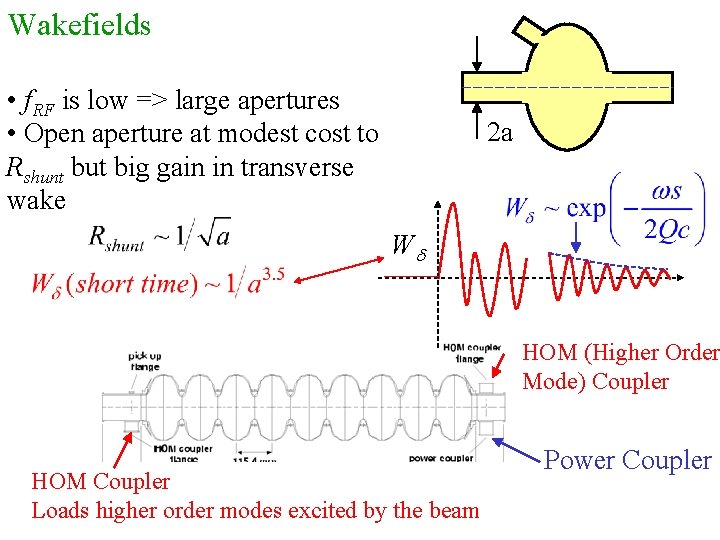
Wakefields • f. RF is low => large apertures • Open aperture at modest cost to Rshunt but big gain in transverse wake 2 a Wd HOM (Higher Order Mode) Coupler HOM Coupler Loads higher order modes excited by the beam Power Coupler

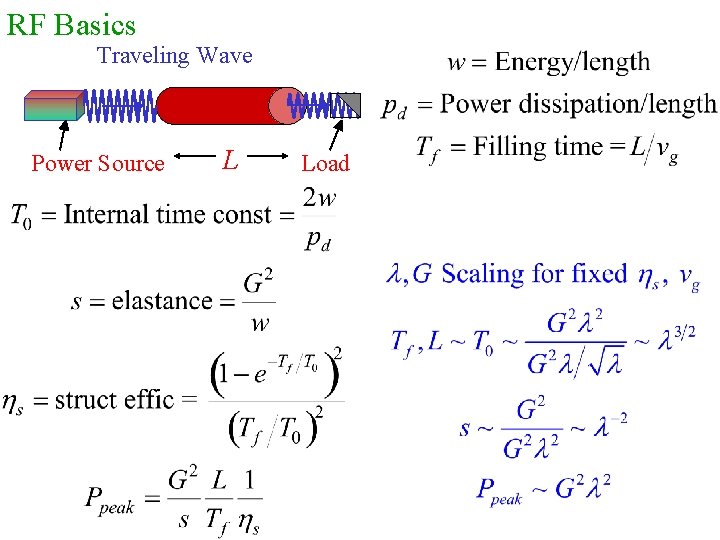
RF Basics Traveling Wave Power Source L Load

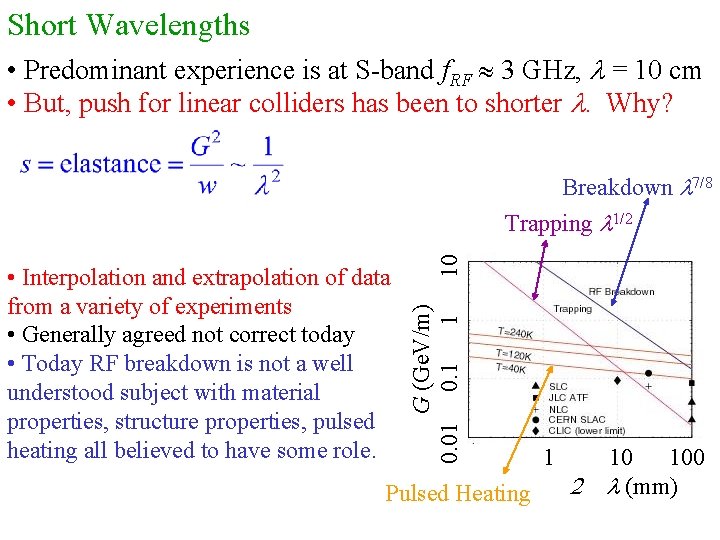
Short Wavelengths • Predominant experience is at S-band f. RF 3 GHz, l = 10 cm • But, push for linear colliders has been to shorter l. Why? G (Ge. V/m) 0. 01 0. 1 1 • Interpolation and extrapolation of data from a variety of experiments • Generally agreed not correct today • Today RF breakdown is not a well understood subject with material properties, structure properties, pulsed heating all believed to have some role. 10 Breakdown l 7/8 Trapping l 1/2 Pulsed Heating 1 10 100 2 l (mm)

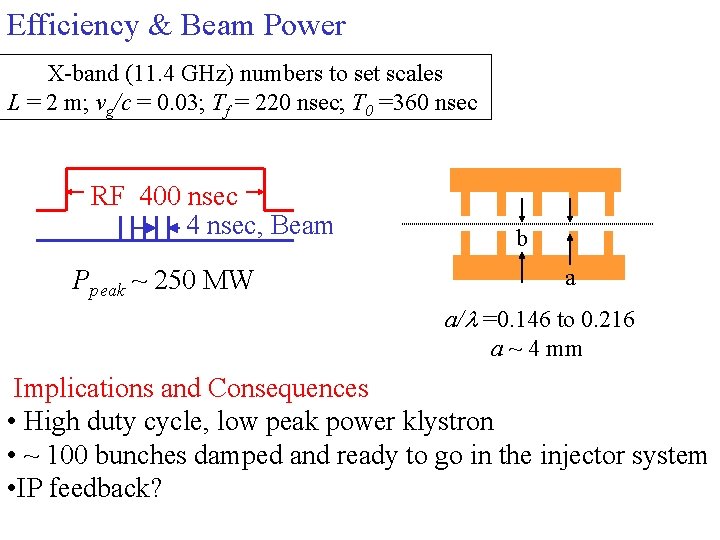
Efficiency & Beam Power X-band (11. 4 GHz) numbers to set scales L = 2 m; vg/c = 0. 03; Tf = 220 nsec; T 0 =360 nsec RF 400 nsec 4 nsec, Beam Ppeak ~ 250 MW b a a/l =0. 146 to 0. 216 a ~ 4 mm Implications and Consequences • High duty cycle, low peak power klystron • ~ 100 bunches damped and ready to go in the injector system • IP feedback?

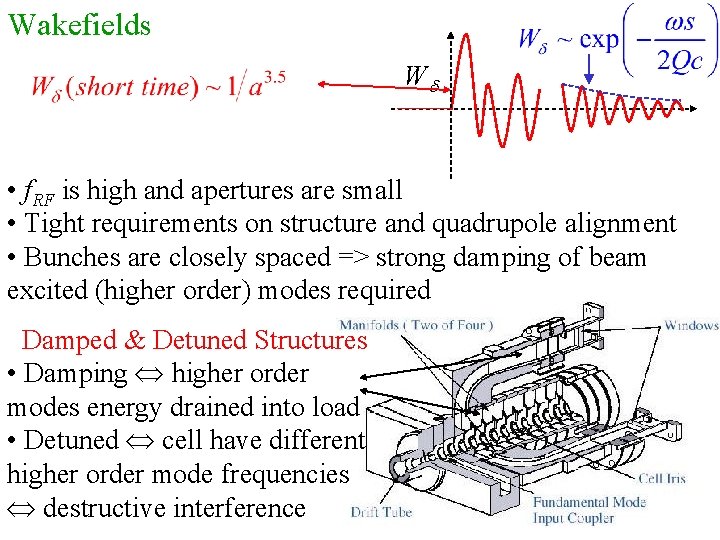
Wakefields Wd • f. RF is high and apertures are small • Tight requirements on structure and quadrupole alignment • Bunches are closely spaced => strong damping of beam excited (higher order) modes required Damped & Detuned Structures • Damping higher order modes energy drained into load • Detuned cell have different higher order mode frequencies destructive interference

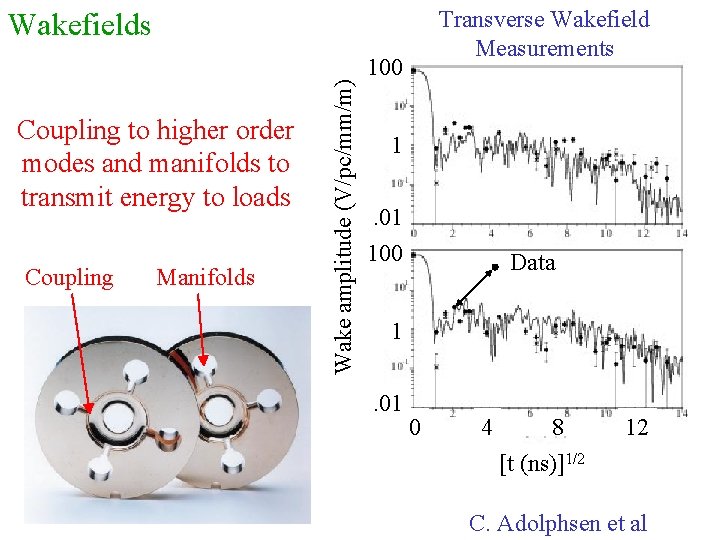
Transverse Wakefield Measurements Coupling to higher order modes and manifolds to transmit energy to loads Coupling Manifolds Wake amplitude (V/pc/mm/m) Wakefields 100 1. 01 100 Data 1. 01 0 4 8 12 [t (ns)]1/2 C. Adolphsen et al

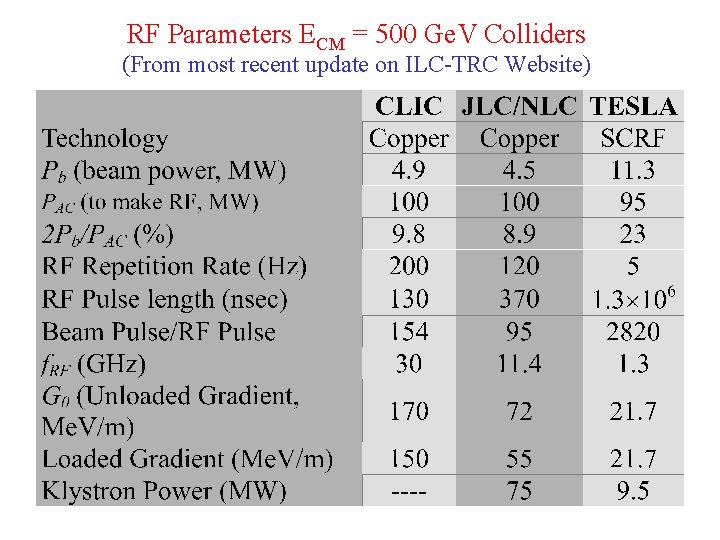
RF Parameters ECM = 500 Ge. V Colliders (From most recent update on ILC-TRC Website)

Progress on Electron-Positron Linear Colliders and Technology Bob Siemann, SLAC 1. 2. 3. 4. 5. 6. 7. Luminosity and the Beam-Beam Interaction Energy Spread, Emittance & Wakefields Superconducting & Room Temperature Linacs RF Power Damping Rings & Bunch Compressors E+ Production & E- Sources Perspective

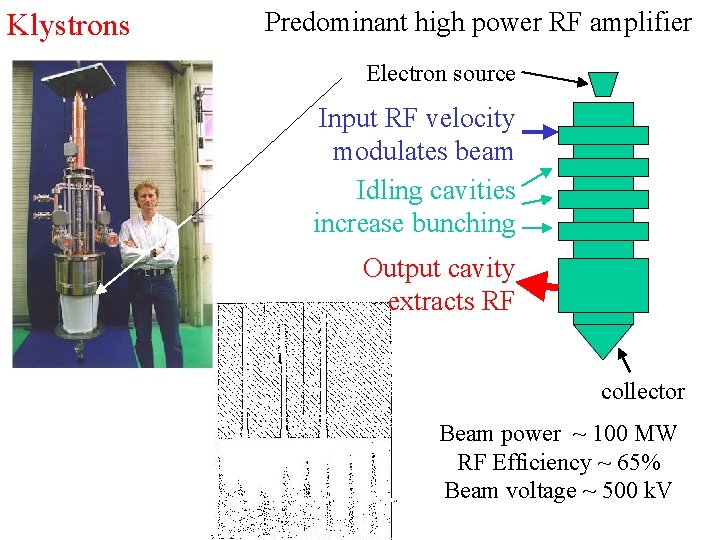
Klystrons Predominant high power RF amplifier Electron source Input RF velocity modulates beam Idling cavities increase bunching Output cavity extracts RF collector Beam power ~ 100 MW RF Efficiency ~ 65% Beam voltage ~ 500 k. V

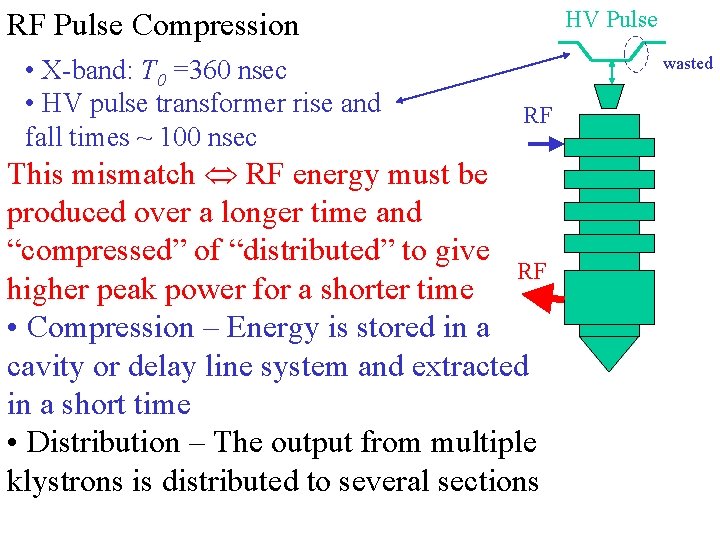
HV Pulse RF Pulse Compression • X-band: T 0 =360 nsec • HV pulse transformer rise and fall times ~ 100 nsec wasted RF This mismatch RF energy must be produced over a longer time and “compressed” of “distributed” to give RF higher peak power for a shorter time • Compression – Energy is stored in a cavity or delay line system and extracted in a short time • Distribution – The output from multiple klystrons is distributed to several sections

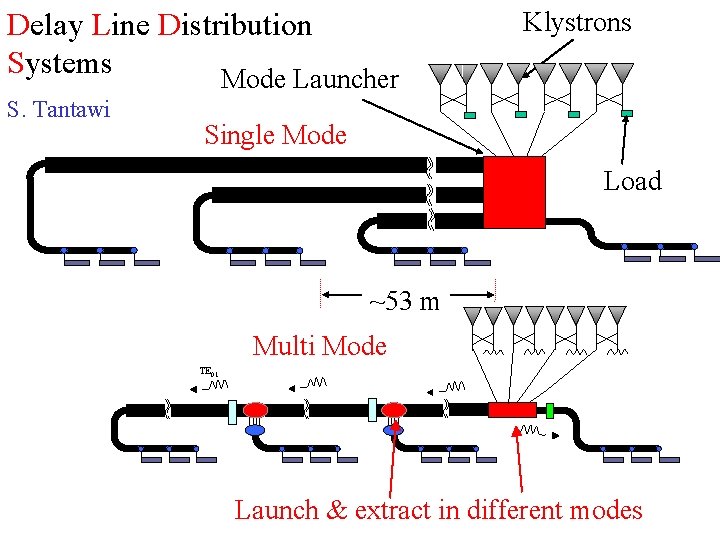
Delay Line Distribution Systems Mode Launcher S. Tantawi Klystrons Single Mode Load ~53 m Multi Mode TE 01 Launch & extract in different modes

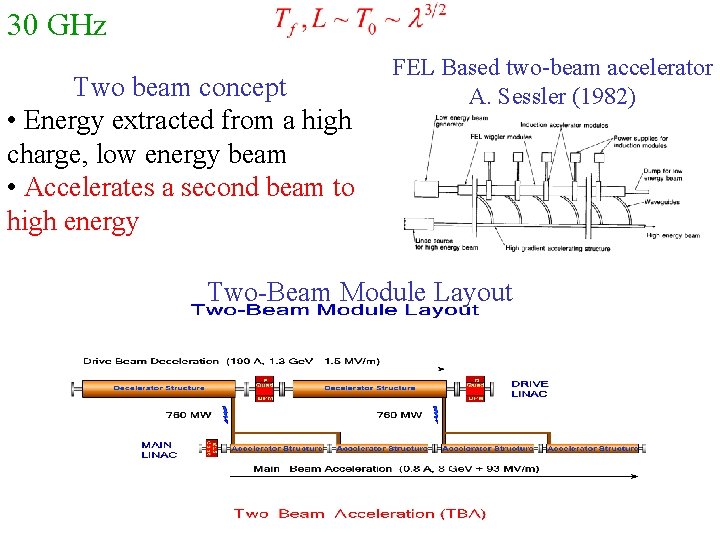
30 GHz Two beam concept • Energy extracted from a high charge, low energy beam • Accelerates a second beam to high energy FEL Based two-beam accelerator A. Sessler (1982) Two-Beam Module Layout

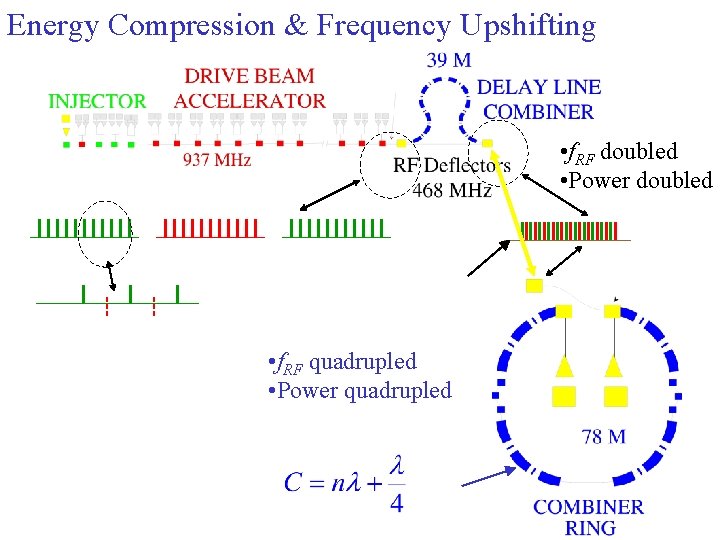
Energy Compression & Frequency Upshifting • f. RF doubled • Power doubled • f. RF quadrupled • Power quadrupled

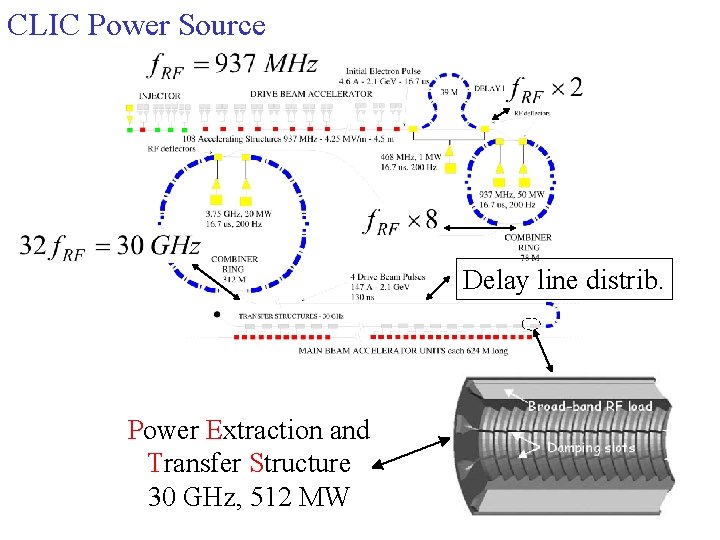
CLIC Power Source Delay line distrib. Power Extraction and Transfer Structure 30 GHz, 512 MW

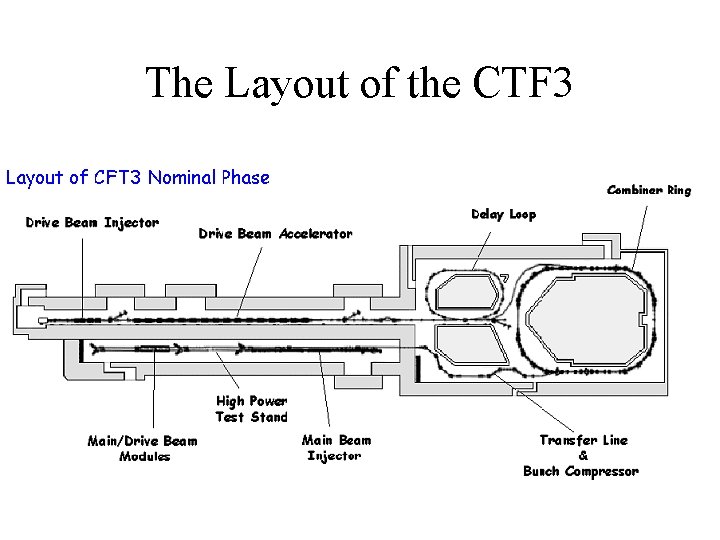
The Layout of the CTF 3

Progress on Electron-Positron Linear Colliders and Technology Bob Siemann, SLAC 1. 2. 3. 4. 5. 6. 7. Luminosity and the Beam-Beam Interaction Energy Spread, Emittance & Wakefields Superconducting & Room Temperature Linacs RF Power Damping Rings & Bunch Compressors E+ Production & E- Sources Perspective

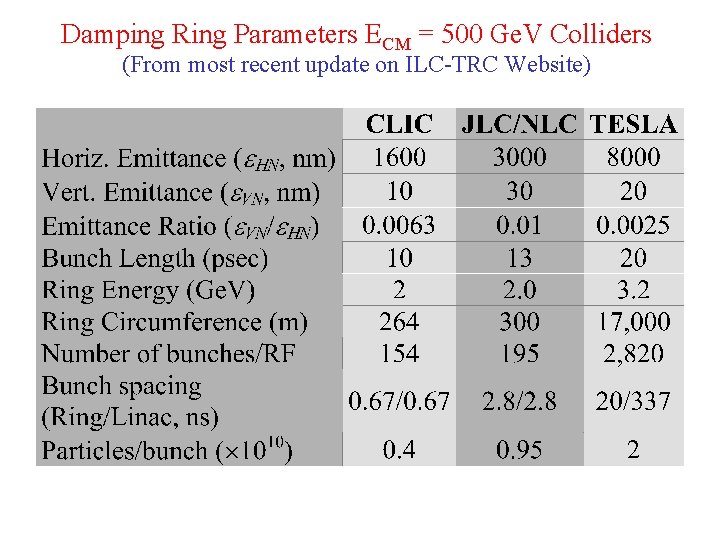
Damping Ring Parameters ECM = 500 Ge. V Colliders (From most recent update on ILC-TRC Website)

Damping Rings Damping rings are dominated by synchrotron radiation • Output beam properties at low intensity are determined by synchrotron radiation t 2 • Liouville’s Theorem does not hold p t 1 o synchrotron radiation dissipation q not Hamiltonian o BUT it holds everywhere downstream, so DR’s determine the minimum emittances

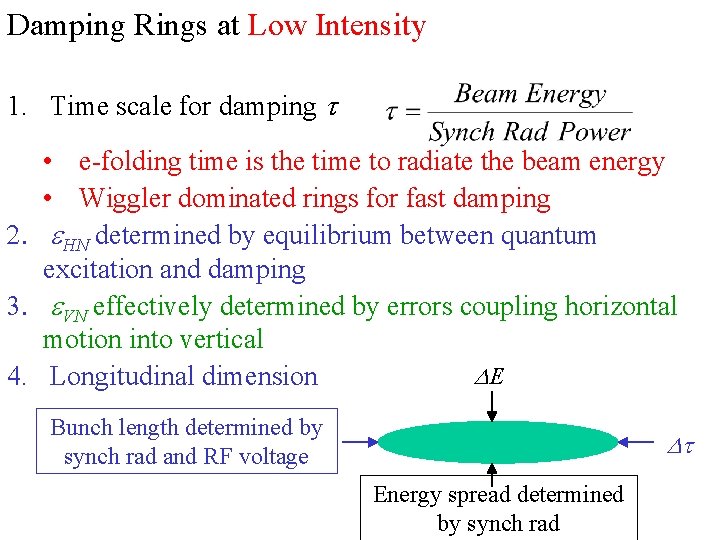
Damping Rings at Low Intensity 1. Time scale for damping t • e-folding time is the time to radiate the beam energy • Wiggler dominated rings for fast damping 2. e. HN determined by equilibrium between quantum excitation and damping 3. e. VN effectively determined by errors coupling horizontal motion into vertical DE 4. Longitudinal dimension Bunch length determined by synch rad and RF voltage Dt Energy spread determined by synch rad

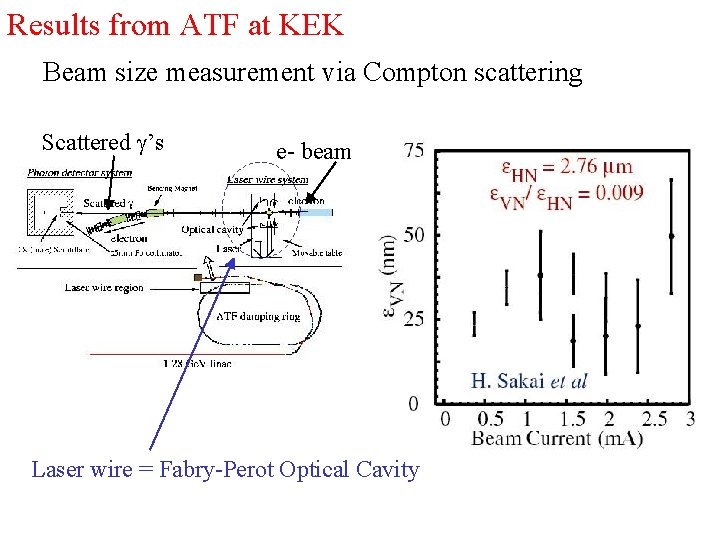
Results from ATF at KEK Beam size measurement via Compton scattering Scattered g’s e- beam Laser wire = Fabry-Perot Optical Cavity

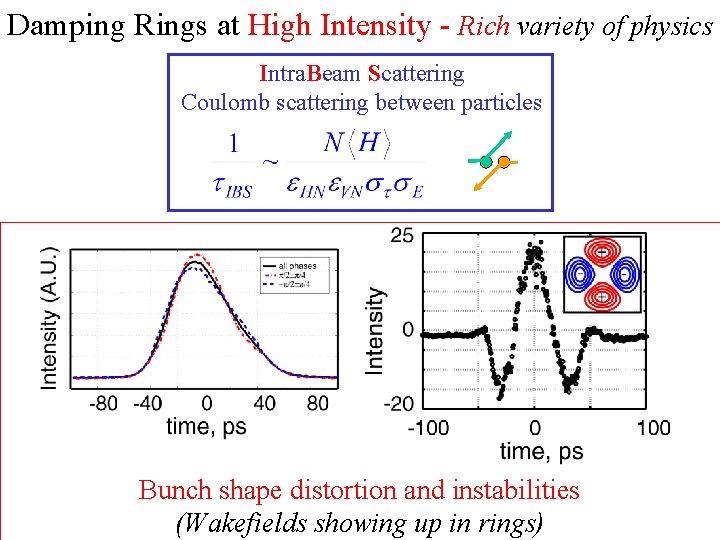
Damping Rings at High Intensity - Rich variety of physics Intra. Beam Scattering Coulomb scattering between particles Bunch shape distortion and instabilities (Wakefields showing up in rings)

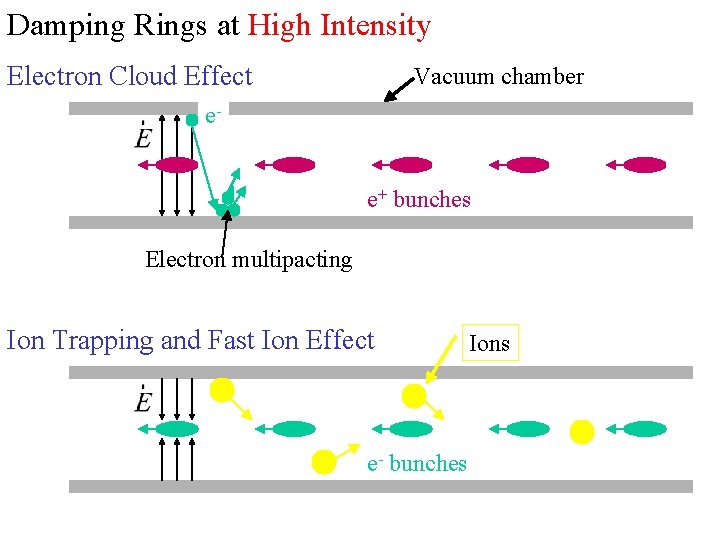
Damping Rings at High Intensity Electron Cloud Effect Vacuum chamber ee+ bunches Electron multipacting Ion Trapping and Fast Ion Effect e- bunches Ions

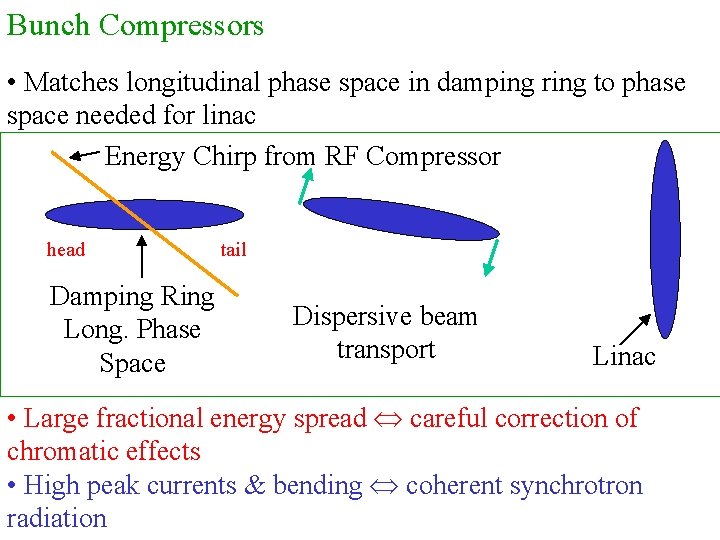
Bunch Compressors • Matches longitudinal phase space in damping ring to phase space needed for linac Energy Chirp from RF Compressor head Damping Ring Long. Phase Space tail Dispersive beam transport Linac • Large fractional energy spread careful correction of chromatic effects • High peak currents & bending coherent synchrotron radiation

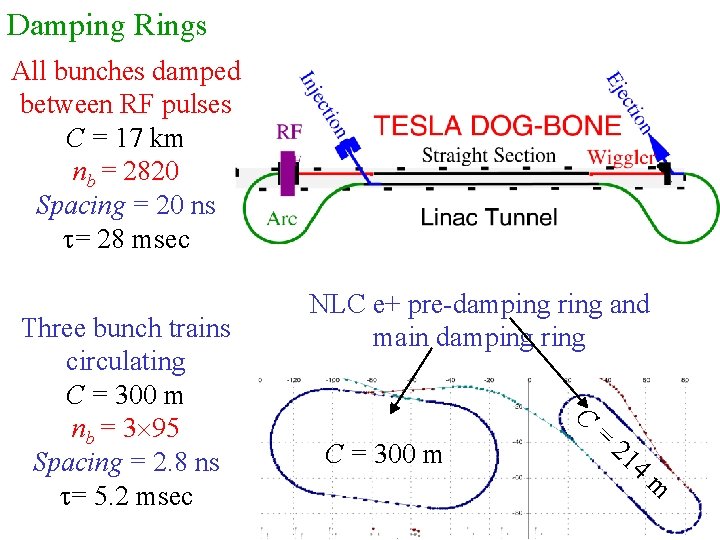
Damping Rings All bunches damped between RF pulses C = 17 km nb = 2820 Spacing = 20 ns t= 28 msec Three bunch trains circulating C = 300 m nb = 3 95 Spacing = 2. 8 ns t= 5. 2 msec NLC e+ pre-damping ring and main damping ring C C = 300 m = 21 4 m

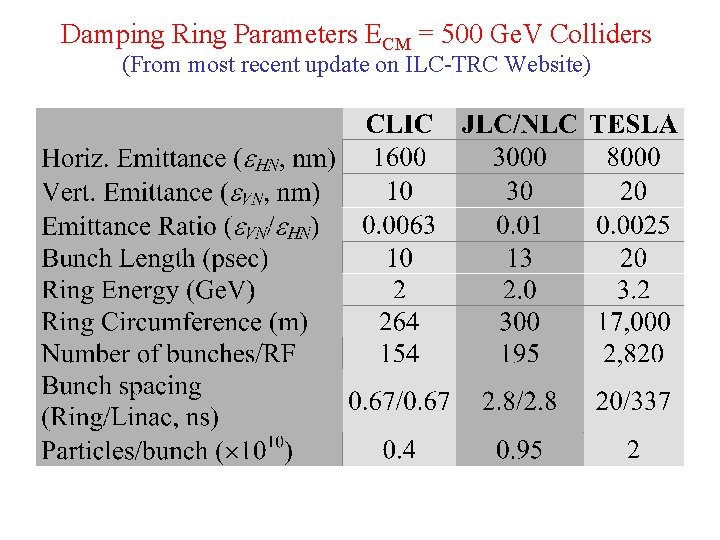
Damping Ring Parameters ECM = 500 Ge. V Colliders (From most recent update on ILC-TRC Website)

Progress on Electron-Positron Linear Colliders and Technology Bob Siemann, SLAC 1. 2. 3. 4. 5. 6. 7. Luminosity and the Beam-Beam Interaction Energy Spread, Emittance & Wakefields Superconducting & Room Temperature Linacs RF Power Damping Rings & Bunch Compressors E+ Production & E- Sources Perspective

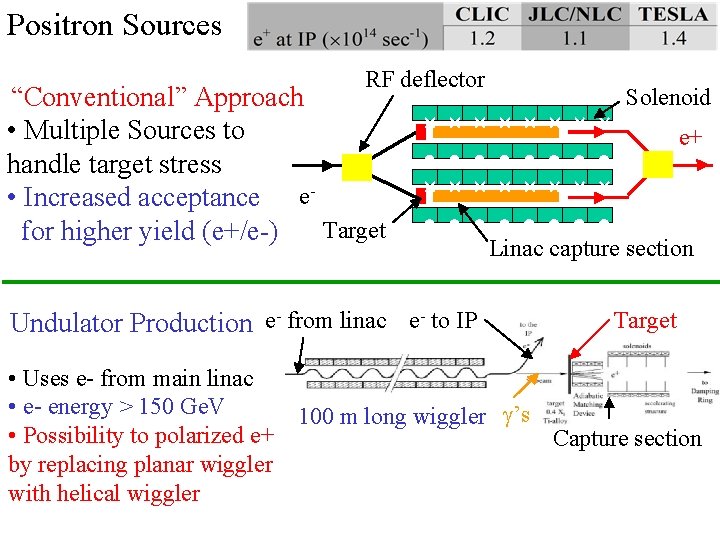
Positron Sources RF deflector “Conventional” Approach • Multiple Sources to handle target stress • Increased acceptance e. Target for higher yield (e+/e-) Solenoid e+ Linac capture section Undulator Production e- from linac e- to IP Target • Uses e- from main linac • e- energy > 150 Ge. V 100 m long wiggler g’s • Possibility to polarized e+ Capture section by replacing planar wiggler with helical wiggler

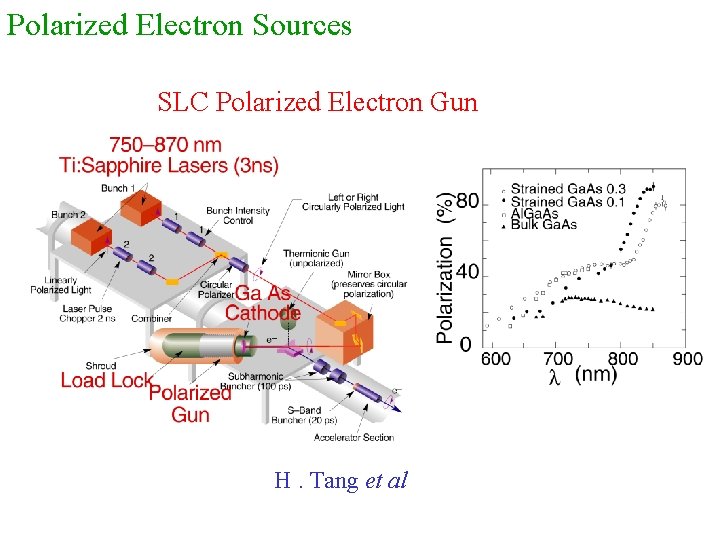
Polarized Electron Sources SLC Polarized Electron Gun H. Tang et al

Progress on Electron-Positron Linear Colliders and Technology Bob Siemann, SLAC 1. 2. 3. 4. 5. 6. 7. Luminosity and the Beam-Beam Interaction Energy Spread, Emittance & Wakefields Superconducting & Room Temperature Linacs RF Power Damping Rings & Bunch Compressors E+ Production & E- Sources Perspective

Linear Colliders - Early History The Concept 1. Maury Tigner, “A Possible Apparatus for Clashing-Beam Experiments”, Nuovo Cimento 37, 1228 (1965) 2. Ugo Amaldi, “A possible scheme to obtain e-e- and e+ecollisions at energies of hundreds of Ge. V”, Physics Letters B 61, 313 (1976) 3. The SLC – The First Realization 4. Burton Richter et al, “The Stanford Linear Collider”, 11 th Int Conf on High-Energy Accelerators, CERN (1980)

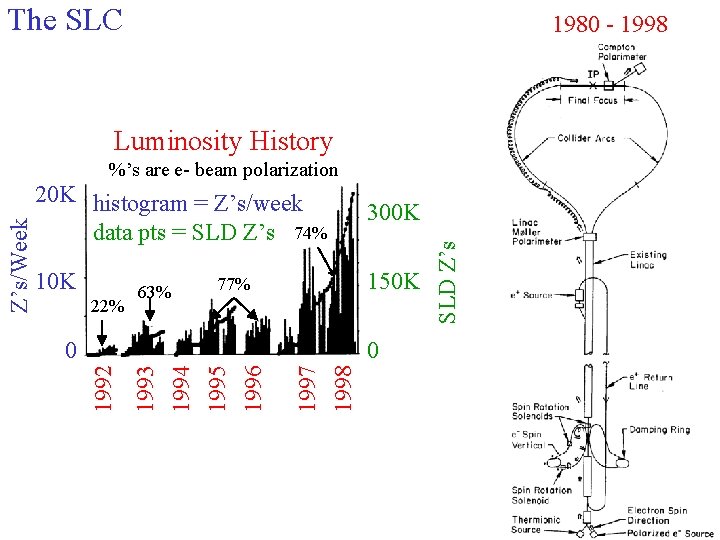
The SLC 1980 - 1998 Luminosity History 300 K 150 K 22% 63% 77% 1997 1998 1996 0 1993 1994 1995 0 SLD Z’s 20 K histogram = Z’s/week data pts = SLD Z’s 74% 1992 Z’s/Week %’s are e- beam polarization

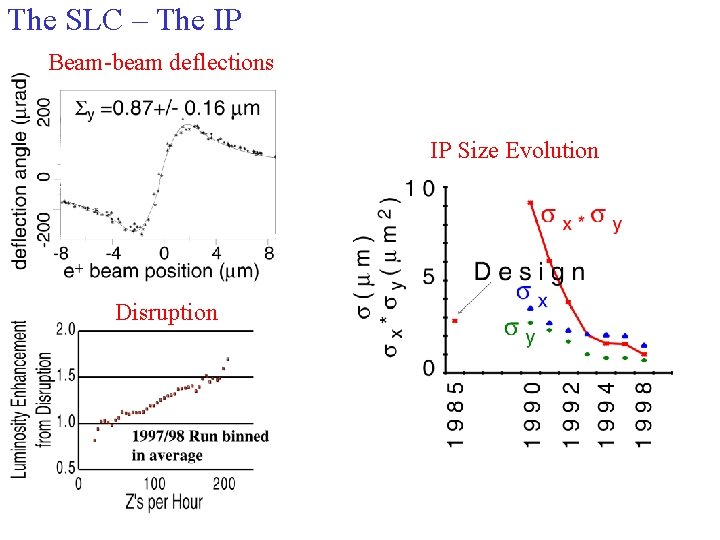
The SLC – The IP Beam-beam deflections IP Size Evolution Disruption

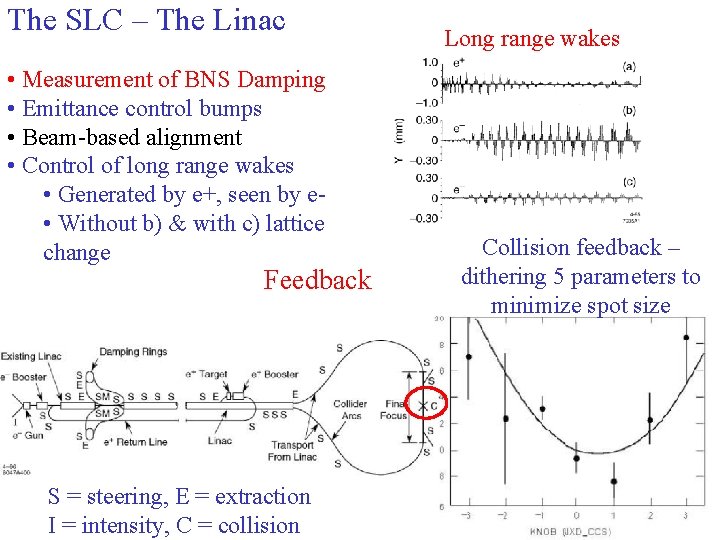
The SLC – The Linac • Measurement of BNS Damping • Emittance control bumps • Beam-based alignment • Control of long range wakes • Generated by e+, seen by e • Without b) & with c) lattice change Feedback S = steering, E = extraction I = intensity, C = collision Long range wakes Collision feedback – dithering 5 parameters to minimize spot size

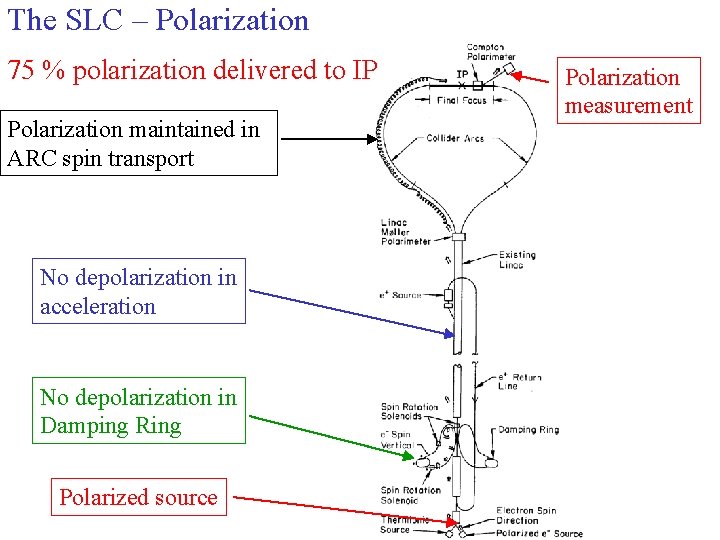
The SLC – Polarization 75 % polarization delivered to IP Polarization maintained in ARC spin transport No depolarization in acceleration No depolarization in Damping Ring Polarized source Polarization measurement

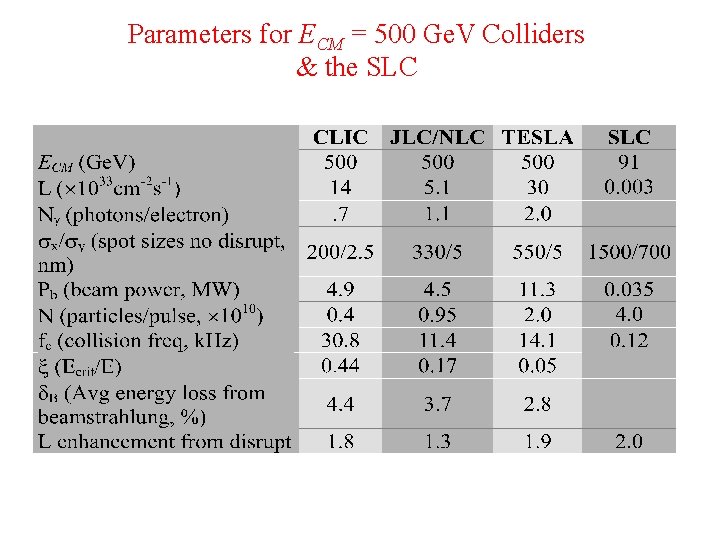
Parameters for ECM = 500 Ge. V Colliders & the SLC