Programozsi alapismeretek 12 elads Programozsi alapismeretek 12 elads

Programozási alapismeretek 12. előadás

Programozási alapismeretek 12. előadás Ø Tapasztalatok ELTE a rendezésről Ø Keresés rendezett sorozatban Ø Rendezettek uniója Ø Rendezettek összefésülése Ø Kiválogatás helyben Ø Szétválogatás helyben Szlávi-Zsakó: Programozási alapismeretek 12. /35

Tapasztalatok a rendezésről ØA ELTE rendezési algoritmusok eredménye egy rendezett sorozat. Vajon lehet-e a korábban megismert feladatokat más-képp megoldani, ha a bemenetük rende -zett? Ø A rendezési algoritmusok többsége „helyben” rendez. Vannak-e más, „helyben” működő algoritmusok? Szlávi-Zsakó: Programozási alapismeretek 12. /35

Keresés rendezett sorozatban Feladat: Egy Y értéket keresünk egy rendezett X sorozatban. Specifikáció: ELTE Ø Bemenet: T-tulajdonság: T(v): =(v=Y) N: Egész, Y: Valami X: Tömb[1. . N: Valami] Konkretizáljuk! Ø Kimenet: Van: Logikai, S: Egész Legyen növekvő! Ø Előfeltétel: N 0 és Rendezett. E(X) Ø Utófeltétel: Van= i(1 i N): X[i]=Y és Van 1 S N és X[S]=Y Ø Definíció (emlékeztető): Rendezett. E(X[1. . N]): = i(1 i<N): X[i] X[i+1] Szlávi-Zsakó: Programozási alapismeretek 12. /35

Keresés rendezett sorozatban Ötlet: ELTE Ha már a keresett elem értékénél nagyobb-nál tartunk, akkor biztos nem lesz a sorozat-ban, megállhatunk. i: =1 i N és X[i]<Y i: =i+1 Van: = i N és X[i]=Y Észrevétel: Van megoldás megálltunk keresés köz-ben, mégpedig azért, mert megtaláltuk a keresett értéket. Szlávi-Zsakó: Programozási alapismeretek 12. /35

Keresés rendezett sorozatban Specifikáció: Ø Bemenet: ELTE N: Egész, Y: Valami X: Tömb[1. . N: Valami] Ø Kimenet: Van: Logikai, S: Egész Ø Előfeltétel: N 0 és Rendezett. E(X) Ø Utófeltétel: Van= i(1 i N): X[i]=Y és Van 1 S N és X[S]=Y Ötlet: Először a középső elemmel hasonlítsunk! Ha nem a keresett, akkor vagy előtte, vagy mögötte kell tovább keresni! Szlávi-Zsakó: Programozási alapismeretek 12. /35

Keresés rendezett sorozatban Algoritmus: ELTE E: =1 U: =N S: =(E+U) div 2 X[S]>Y X[S]<Y U: =S– 1 E: =S+1 E U és X[S] Y Van: =X[S]=Y Szlávi-Zsakó: Programozási alapismeretek 12. ØItt akkor van megoldás, ha megtaláltuk a keresett értéket. /35

Keresés rendezett sorozatban Kérdések: Ø Ha ELTE több egyforma elem is van a sorozatban, akkor ez a módszer melyiket találja meg? Ø Hogyan lehetne az összes Y-értékű elemet megtalálni? Ø Hány lépés alatt találjuk meg a keresett elemet? Szlávi-Zsakó: Programozási alapismeretek 12. /35

Rendezettek uniója Összefuttatás. Feladat: Adott két rendezett halmaz, adjuk meg az uniójukat! ELTE Specifikáció: Ø Bemenet: N, M: Egész, X: Tömb[1. . N: Valami], Y: Tömb[1. . M: Valami] N+M Ø Kimenet: Db: Egész, Z: Tömb[1. . Db: Valami] Ø Előfeltétel: N, M 0 és Halmaz. E(X) és Halmaz. E(Y) és Rendezett. E(X) és Szlávi-Zsakó: Programozási alapismeretek 12. /35

Rendezettek uniója Ø Utófeltétel: ELTE és i(1≤i≤Db): Z[i] X vagy Z[i] Y és Halmaz. E(Z) és Rendezett. E(Z) Ø Definíció (emlékeztető): Halmaz. E(X[1. . N]): = i j [1. . N]: X[i] X[j] Ötlet: Az eredmény első eleme vagy az X, vagy az Y első eleme lehet. Ha ezt az eredménybe tesz-szük, a maradékra Szlávi-Zsakó: Programozási alapismeretek 12. /35

Rendezettek uniója Algoritmus elé: Ø Amíg van mit hasonlítani: ELTE Ø Ha már nincs mit hasonlítani: Szlávi-Zsakó: Programozási alapismeretek 12. /35

Rendezettek uniója Algoritmus 1: i: =1 j: =1 Db: =0 ELTE i N és j M Db: =Db+1 X[i]<Y[j] X[i]=Y[j] X[i]>Y[j] Z[Db]: =X[i] Z[Db]: =Y[j ] i: =i+1 j: =j+1 … Szlávi-Zsakó: Programozási alapismeretek 12. /35

Rendezettek uniója … i N ELTE Db: =Db+1 Z[Db]: =X[i] i: =i+1 j M Db: =Db+1 Z[Db]: =Y[j] j: =j+1 ØEz a két ciklus nem kellene, ha tudnánk, hogy X és Y utolsó elemei egyenlők! Szlávi-Zsakó: Programozási alapismeretek 12. /35

Rendezettek uniója Algoritmus 2: i: =1 j: =1 Db: =0 X[N+1]: =+ Y[M+1]: =+ ELTE … és utoljára? Z[Db]: =+ i N+1 és j M+1 Db: =Db+1 X[i]<Y[j] X[i]=Y[j] X[i]>Y[j] Z[Db]: =X[i] Z[Db]: =Y[j ] i: =i+1 j: =j+1 Szlávi-Zsakó: Programozási alapismeretek 12. /35

Rendezettek uniója Algoritmus 2 javítása: ELTE i: =1 j: =1 Db: =0 X[N+1]: =+ Y[M+1]: =+ i<N+1 vagy j<M+1 Db: =Db+1 X[i]<Y[j] X[i]=Y[j] X[i]>Y[j] Z[Db]: =X[i] Z[Db]: =Y[j ] i: =i+1 j: =j+1 Szlávi-Zsakó: Programozási alapismeretek 12. /35

Rendezettek uniója Kérdések: Ø Jobb ELTE lett ez a módszer az előzőnél? Hány lépés alatt kapjuk meg a megoldást? Ø Meg lehetne ugyanezt tenni a metszettel is? Tapasztalat: ez a módszer a kimenet szerint halad egye-sével és nem a bemenet szerint (mint a ko-rábbiak). Szlávi-Zsakó: Programozási alapismeretek 12. /35

Rendezettek összefésülése Feladat: Adott két rendezett halmaz, adjuk meg az összefésülésüket! ELTE Specifikáció: Ø Bemenet: N, M: Egész, X: Tömb[1. . N: Valami], Y: Tömb[1. . M: Valami] Ø Kimenet: Z: Tömb[1. . N+M: Valami] Ø Előfeltétel: N, M 0 és Rendezett. E(X) és Rendezett. E(Y) Szlávi-Zsakó: Programozási alapismeretek 12. /35

Rendezettek összefésülése Ø Utófeltétel: Z Permutáció(X+Y) és Rendezett. E(Z) Ötlet: ELTE A megoldás olyan, mint az összefuttatás, csak az egyforma elemeket is berakjuk az eredménybe. Szlávi-Zsakó: Programozási alapismeretek 12. /35

Rendezettek összefésülése Algoritmus: ELTE i: =1 j: =1 Db: =0 X[N+1]: =+ Y[M+1]: =+ i<N+1 vagy j<M+1 Db: =Db+1 X[i] Y[j] I N Z[Db]: =X[i] Z[Db]: =Y[j] i: =i+1 j: =j+1 Szlávi-Zsakó: Programozási alapismeretek 12. /35

Kiválogatás helyben Specifikáció: Ø Bemenet: ELTE N: Egész, X: Tömb[1. . N: Valami] Ø Kimenet: Db: Egész, X’: Tömb[1. . N: Valami] Ø Előfeltétel: N 0 Ø Utófeltétel: és X’[1. . Db] X és i (1≤i≤Db): T(X’[i]) Szlávi-Zsakó: Programozási alapismeretek 12. /35

Kiválogatás helyben Algoritmus: Db: =0 ELTE i=1. . N T(X[i]) I Db: =Db+1 X[Db]: =X[i] N Megjegyzés: Itt olyan helyre tesszük a kiválogatott elemet, amire már nincs szükségünk. Szlávi-Zsakó: Programozási alapismeretek 12. /35

Szétválogatás helyben Specifikáció: Ø Bemenet: ELTE N: Egész, X: Tömb[1. . N: Valami] Ø Kimenet: Db: Egész, X’: Tömb[1. . N: Valami] Ø Előfeltétel: N 0 Ø Utófeltétel: Db= és X’ Permutáció(X) és i (1≤i≤Db): T(X’[i]) és i (Db+1≤i≤N): nem T(X’[i]) Ø Definíció (emlékeztető): Permutáció(Z): = Z elemeinek Szlávi-Zsakó: Programozási alapismeretek 12. /35

Szétválogatás helyben Algoritmikus ötlet: 1. Vegyük ELTE ki a sorozat első elemét: Oxxxxxx 2. Keresünk hátulról egy elemet, amit előre kell tennünk (mert T tulajdonságú): Oxxxxxx 3. A megtalált elemet tegyük az előbb keletke-zett lyukba! Szlávi-Zsakó: Programozási alapismeretek 12. /35

Szétválogatás helyben 4. Most keletkezett egy lyuk hátul, az előbb be-töltött lyuktól indulva elölről keressünk hátra teendő elemet: xxxxx. Oxx ELTE 5. A megtalált elemet tegyük a hátul levő lyukba, majd újra hátulról kereshetünk! 6. … 7. Befejezzük a keresést, ha valahonnan elértük a lyukat, majd erre a helyre a kivettet vissza-tesszük. Szlávi-Zsakó: Programozási alapismeretek 12. /35

Szétválogatás helyben Algoritmus: e: =1 u: =N Y: =X[e] ELTE e<u Hátulról. Keres(e, u, Van) Van I X[e]: =X[u] e: =e+1 Elölről. Keres(e, u, Van) Van I X[u]: =X[e] u: =u– 1 … Szlávi-Zsakó: Programozási alapismeretek 12. N N /35

Szétválogatás helyben … X[e]: =Y ELTE I T(Y) Db: =e Szlávi-Zsakó: Programozási alapismeretek 12. Db: =e– 1 N /35

Szétválogatás helyben Elölről. Keres(e, u: Egész, Van: Logikai ) ELTE e<u és T(X[e]) e: =e+1 Van: =e<u Hátulról. Keres(e, u: Egész, Van: Logikai) e<u és nem T(X[u]) u: =u– 1 Van: =e<u Szlávi-Zsakó: Programozási alapismeretek 12. /35

Hatékonyságvizsgálat táblázatkezelővel Ø Ötlet: 1. A ELTE táblázatkezelők importálnak, pl. CSV-formátumú fájlt. 2. A Comma Separated Value (CSV) = egy „mezei” text fájl, amelyben minden önálló adatot pontosvessző követ. 3. Egyszerű olyan C++ programot írni, amely a táblázatolandó adatokat „CSV-esítve” ír text fájlba. Szlávi-Zsakó: Programozási alapismeretek 12. /35

Hatékonyságvizsgálat táblázatkezelővel Ø Példafeladat: Az unió és az összefuttatás tételek haté-konyságának összevetése. ELTE Ø Hatékonysági „dimenzió”: tömbbeli elemek összehasonlításszáma Szlávi-Zsakó: Programozási alapismeretek 12. /35

Hatékonyságvizsgálat táblázatkezelővel Ø Megoldásvázlat: 1. Mindkét ELTE algoritmusban számoljuk a tömb-elemösszehasonlításokat. 2. Néhány (jól kiválasztott, vagy az összes) N, M-elemű sorozatra lefuttatjuk és szám-láljuk a hasonlításokat; és CSV-fájlba írjuk az eredményeket. Szlávi-Zsakó: Programozási alapismeretek 12. /35

Hatékonyságvizsgálat táblázatkezelővel Ø Egy lehetséges eredmény a táblázat-kezelőben – unió: Numerikusan ELTE Szlávi-Zsakó: Programozási alapismeretek 12. /35

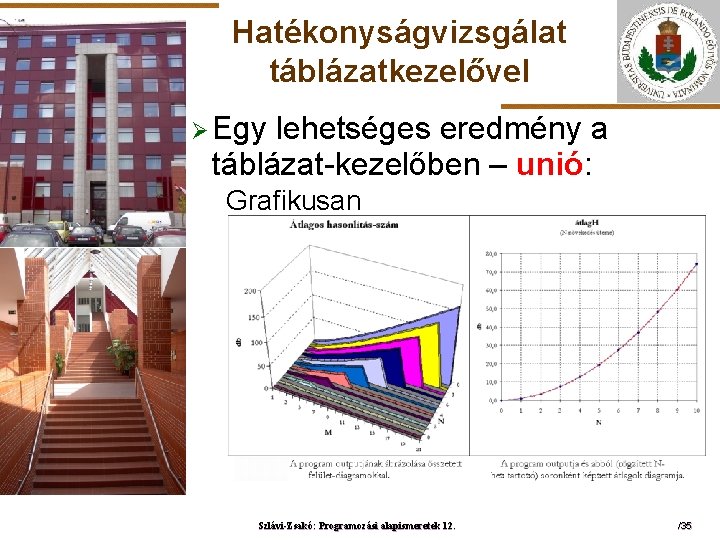
Hatékonyságvizsgálat táblázatkezelővel Ø Egy lehetséges eredmény a táblázat-kezelőben – unió: Grafikusan ELTE Szlávi-Zsakó: Programozási alapismeretek 12. /35

Hatékonyságvizsgálat táblázatkezelővel Ø Egy lehetséges eredmény a táblázat-kezelőben – összefuttatás: ELTE Numerikusan Szlávi-Zsakó: Programozási alapismeretek 12. /35

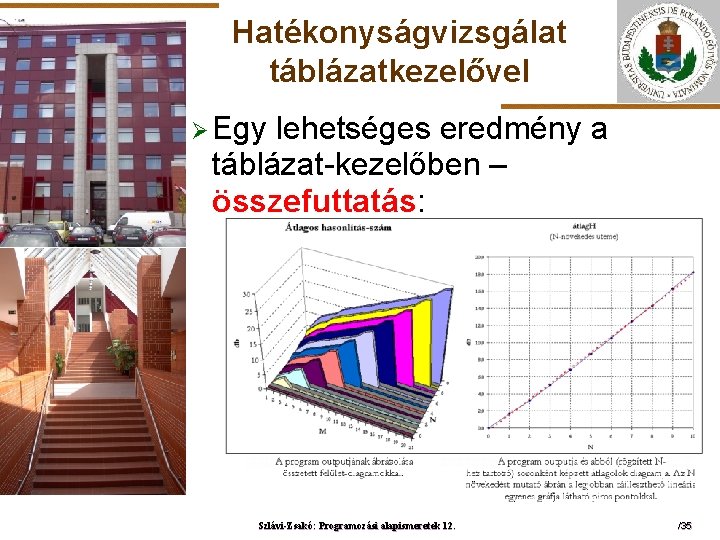
Hatékonyságvizsgálat táblázatkezelővel Ø Egy lehetséges eredmény a táblázat-kezelőben – összefuttatás: ELTE Grafikusan Szlávi-Zsakó: Programozási alapismeretek 12. /35

Programozási alapismeretek 12. előadás vége