Programming Training Main Points Python Turtle Fractals Functions

Programming Training Main Points: - Python Turtle - Fractals

Functions Python function = code to solve a problem - problem’s inputs are function’s arguments - problem’s outputs are calculated and returned - function philosophy write one and use multiple times () represents function.

Screen The screen is a rectangle of pixels on which we can draw. The screen origin is usually in the centre. Each pixel will have two coordinates which are float numbers.

Python Turtle turtle – a Python module / library for drawing. What can turtles (as animals) do? Move forward or backward. Turn left or right. Retreat the head into the shell. Turtle-like Graphics Pens have: x, y give the turtle pen coordinates. dir the direction to go in radians. pen the pen’s status (pen=1 draws line)

Python Turtle turtle – a Python module / library for drawing. Function to Move and Draw forward(d) – pen moves forward for distance d on the direction to go backward(d) – pen moves backward for distance on the direction to go right(angle) – pen turns right with angle (degrees) left(angle) – pen turns left with angle (degrees) goto(x, y) – pen moves to the point (x, y) drawing a line dot(size, color) – pen draws a dot of specified size with the given color circle(radius) – pen draws a circle with the specified radius

Python Turtle turtle – a Python module / library for drawing. Function to Control the penup() – pen moves up so no drawing pendown() – pen goes down so it can draw width(w) – sets the thickness of the line color(colorname) – pen color is set as colorname color(r, g, b) – the color is set based on the r, g, b values.

Python Turtle turtle – a Python module / library for drawing. Function to Control the Screen bgcolor(color) – the screen background color is set to color. clear() – the screen is cleared. screensize() – it returns the width and the height of the screen

Python Turtle How to work with: 1. Make a pen object pen = Pen() 2. Set the pen features like color, width, etc pen. color(‘red’) pen. width(3) 3. Make you drawing using the move/draw functions pen. forward(100) pen. left(90)

Python Turtle 1. What is the outcome of pen. forward(100) 1. Can be re written as for i in range(4) : pen. left(90) pen. forward(100) pen. left(90)

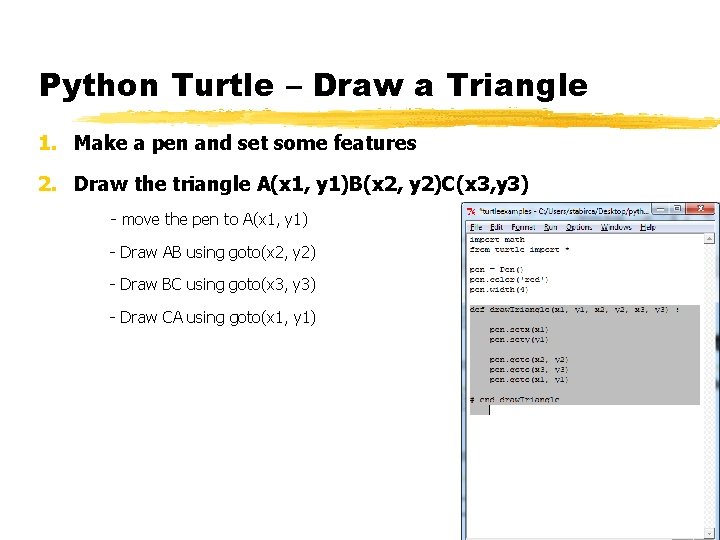
Python Turtle – Draw a Triangle 1. Make a pen and set some features 2. Draw the triangle A(x 1, y 1)B(x 2, y 2)C(x 3, y 3) - move the pen to A(x 1, y 1) - Draw AB using goto(x 2, y 2) - Draw BC using goto(x 3, y 3) - Draw CA using goto(x 1, y 1)

Python Turtle – Draw a Random Circle 1. random a new module to generate random numbers random. randint(a, b) generate a random integer between a and b random() generate a random float between [0, 1) 2. Drawing a random circle - get a random radius - get a random color - get a random width - draw the circle

Turtle Random Art 1. Develop methods to draw random shapes 2. Drawing few similar random shapes in your screen 3. Draw 30 random circles + 20 random triangles

Python Recursive Functions A Python function call any known / seen function from the imported modules or from the file. A function is recursive when it calls itself. Important Rule: A recursive method must have - a termination step that solves directly the problem - a recursion step.

Python Recursive Functions Fibonacci sequence: 1, 1, 2, 3, 5, 8, 13, 21, … fib(0) = fib(1) = 1 and fib(n) = fib(n-1)+ fib(n-2) def fib(n): # termination if n== 0 or n==1 : return 1 # endif return fib(n-1) + fib(n-2) # end fib

Recursive / Turtle Graphics 1. Define Recursively the figure Fn. - Termination: give the shape of F 0 (point, line, etc) - Recursion: define Fn based on Fn-1. 2. Use a Turtle object to draw the figure. - The direction of the Turtle object must be preserved. Turtle Geometry represents the simplest way to construct geometrical fractals. Important Fractals: Trees, Koch’s curves, Sierpinski’s curves etc.

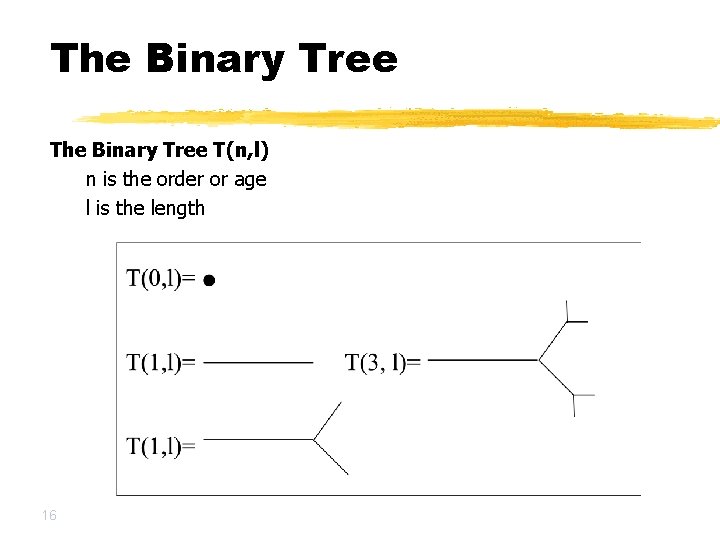
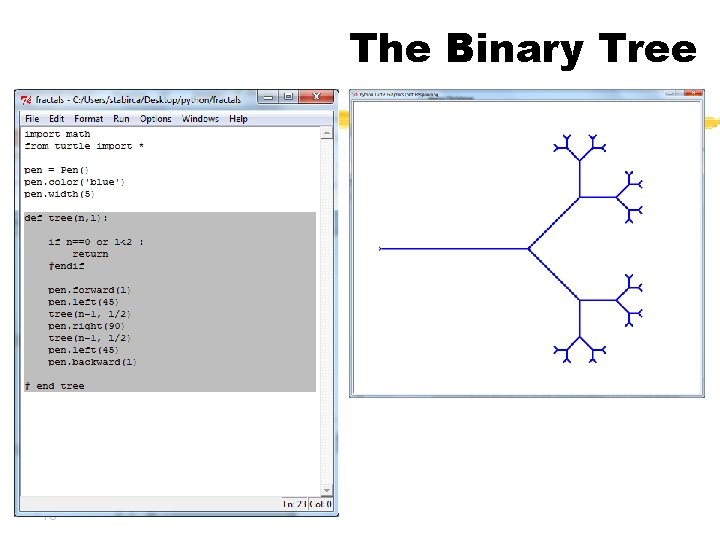
The Binary Tree T(n, l) n is the order or age l is the length 16

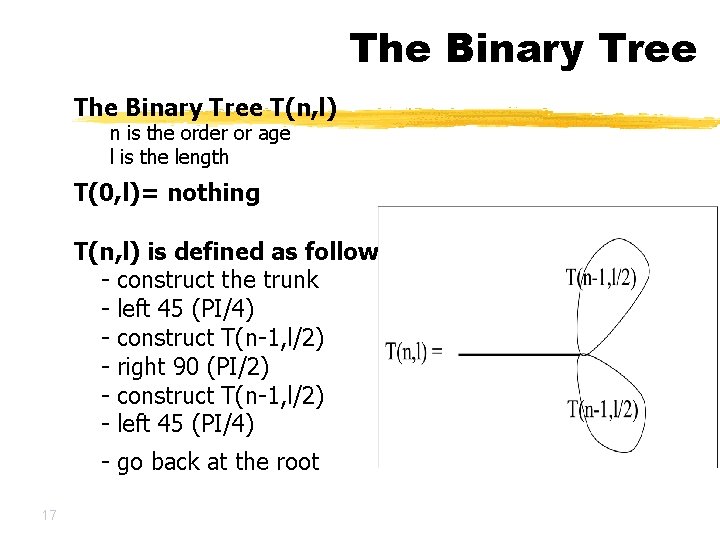
The Binary Tree T(n, l) n is the order or age l is the length T(0, l)= nothing T(n, l) is defined as follows: - construct the trunk - left 45 (PI/4) - construct T(n-1, l/2) - right 90 (PI/2) - construct T(n-1, l/2) - left 45 (PI/4) - go back at the root 17

The Binary Tree 18

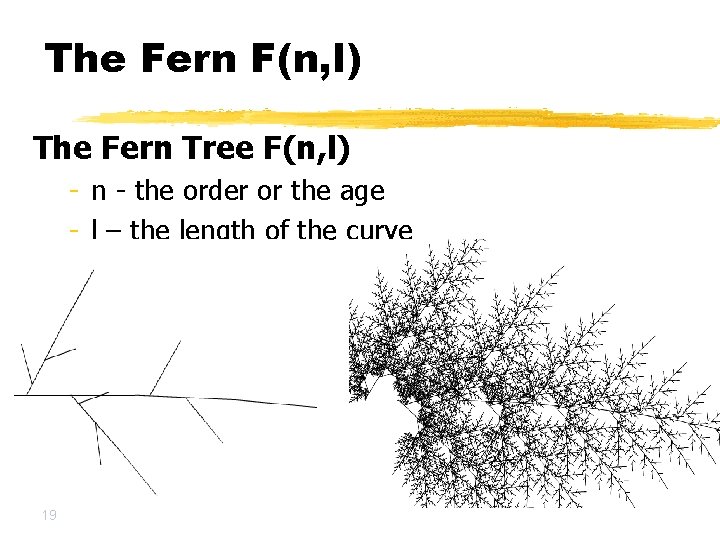
The Fern F(n, l) The Fern Tree F(n, l) - n - the order or the age - l – the length of the curve 19

The Fern F(n, l) - n - the order or the age - l – the length of the curve The Fern F(n, l) is a tree with 3 asymmetric branches. The Fern depends - the braches angles and the branches trunks 20

The Fern F(n, l) is defined by: - F(0, l) is a dot or nothing. - F(n, l) is recursively defined by: 21 - Forward (0. 3*l) Left 55; Construct F(n-1, l/2); Right 55 Forward (0. 7*l) Right 40; Construct F(n-1, l/2); Left 40 Forward l Left 5; Construct F(n-1, 0. 8*l); Right 5 Backward 2*l

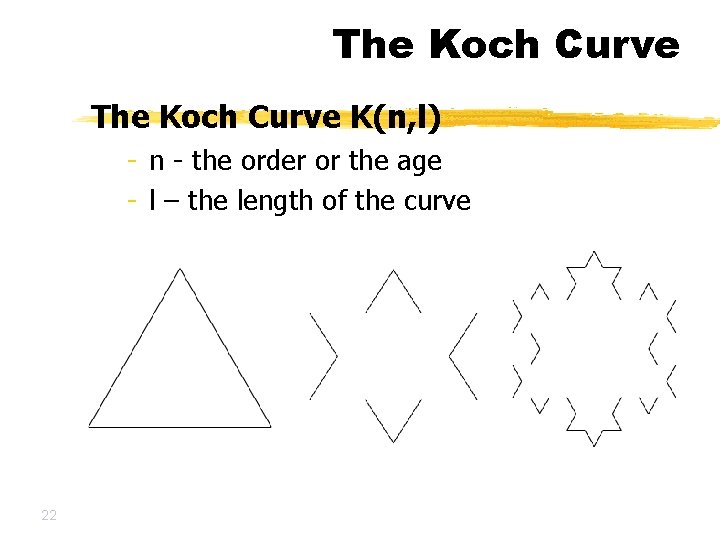
The Koch Curve K(n, l) - n - the order or the age - l – the length of the curve 22

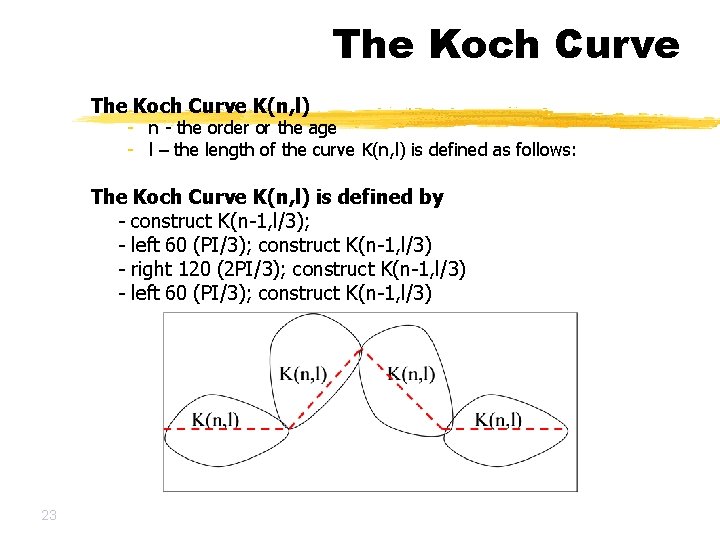
The Koch Curve K(n, l) - n - the order or the age - l – the length of the curve K(n, l) is defined as follows: The Koch Curve K(n, l) is defined by - construct K(n-1, l/3); - left 60 (PI/3); construct K(n-1, l/3) - right 120 (2 PI/3); construct K(n-1, l/3) - left 60 (PI/3); construct K(n-1, l/3) 23

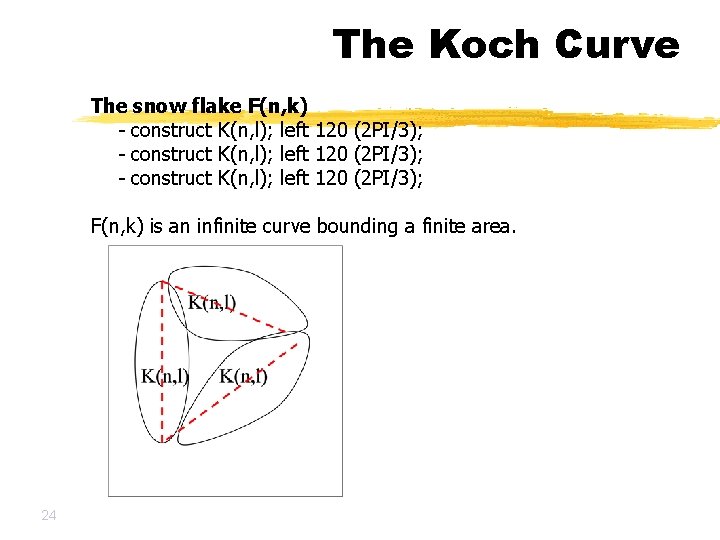
The Koch Curve The snow flake F(n, k) - construct K(n, l); left 120 (2 PI/3); F(n, k) is an infinite curve bounding a finite area. 24

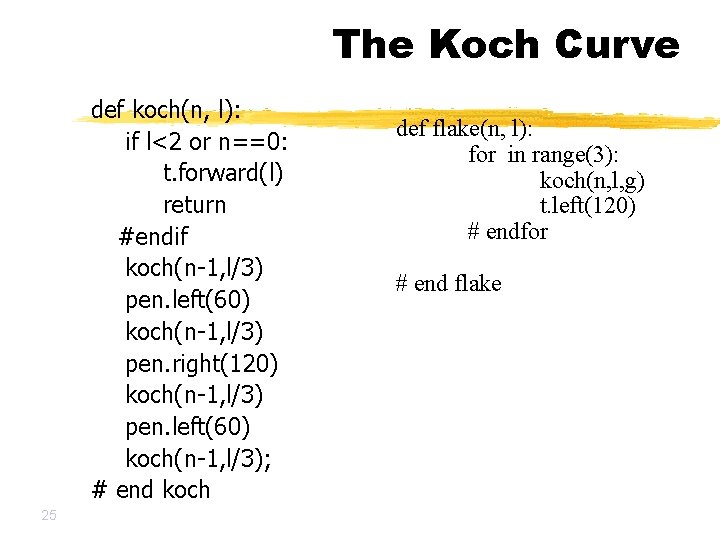
The Koch Curve def koch(n, l): if l<2 or n==0: t. forward(l) return #endif koch(n-1, l/3) pen. left(60) koch(n-1, l/3) pen. right(120) koch(n-1, l/3) pen. left(60) koch(n-1, l/3); # end koch 25 def flake(n, l): for in range(3): koch(n, l, g) t. left(120) # endfor # end flake

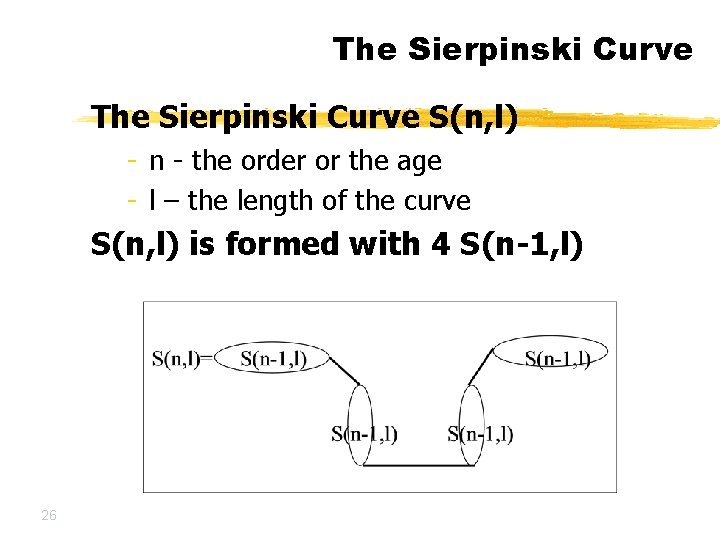
The Sierpinski Curve S(n, l) - n - the order or the age - l – the length of the curve S(n, l) is formed with 4 S(n-1, l) 26

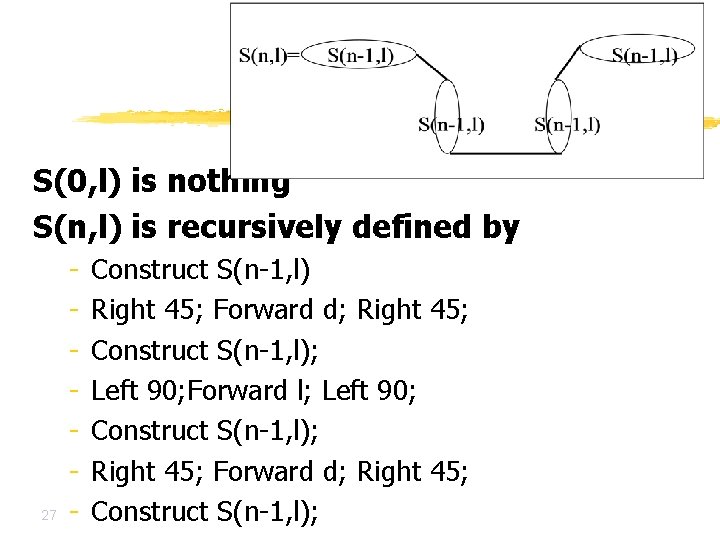
The Sierpinski Curve S(0, l) is nothing S(n, l) is recursively defined by 27 - Construct S(n-1, l) Right 45; Forward d; Right 45; Construct S(n-1, l); Left 90; Forward l; Left 90; Construct S(n-1, l); Right 45; Forward d; Right 45; Construct S(n-1, l);

To do List 1. 2. Solve the HW problems. Read more about the turtle module