Programming Paradigms Logic Programming Paradigm Correctness Efficiency t

Programming Paradigms Logic Programming Paradigm Correctness > Efficiency t. k. prasad@wright. edu http: //www. knoesis. org/tkprasad/ cs 774 (Prasad) L 1 LP 1

Programming Paradigm A way of conceptualizing what it means to perform computation and how tasks to be carried out on the computer should be structured and organized. • • cs 774 (Prasad) Imperative : Functional : Logical : Object-Oriented : Machine-model based Equations; Expression Evaluation First-order Logic Deduction Programming with Data Types L 1 LP 2

Imperative Style vs Declarative Style • Imperative programs – Description of WHAT is to be computed is inter-twined with HOW it is to be computed. – The latter involves organization of data and the sequencing of instructions. • Declarative Programs – Separates WHAT from HOW. – The former is programmer’s responsibility; the latter is interpreter’s/compiler’s responsibility. cs 774 (Prasad) L 1 LP 3

• What : Intent – Value to be computed: a+b+c • How : Details – Recipe for computing the value • Intermediate Code – T : = a + b; T : = T + c; – T : = b + c; T : = a + T; • Accumulator Machine – Load a; Add b; Add c; • Stack Machine – Push a; Push b; cs 774 (Prasad) Add; L 1 LP Push c; Add; 4

Role of variable • In declarative style, a • In imperative style, a variable stands for an variable is a location arbitrary value , and is that can hold a value, used to abbreviate an and can be changed infinite collection of through an assignment. equations. x : = x + 1; 0+0=0 0+1=1 … for all x : 0 + x = x cs 774 (Prasad) � Declarative variable can be viewed as assign-only- once imperative variable. L 1 LP 5

Logic Programming Paradigm • Integrates Data and Control Structures edge(a, b). edge(a, c). edge(c, a). path(X, X). path(X, Y) : - edge(X, Y). path(X, Y) : - edge(X, Z), path(Z, Y). cs 774 (Prasad) L 1 LP 6

Logic Programming • A logic program defines a set of relations. This “knowledge” can be used in various ways by the interpreter to solve different queries. • In contrast, the programs in other languages also make explicit HOW the “declarative knowledge” is used to solve the query. cs 774 (Prasad) L 1 LP 7

Append in Prolog append([], L, L). append([ H | T ], L, [ H | R ]) : append(T, L, R). • True statements about append relation. • “. ” and “: -” are logical connectives that stand for “and” and “if” respectively. • Uses pattern matching. • “[]” and “|” stand for empty list and cons operation. cs 774 (Prasad) L 1 LP 8

Different Kinds of Queries • Verification – sig: list x list -> boolean • append([1], [2, 3], [1, 2, 3]). • Concatenation – sig: list x list -> list • append([1], [2, 3], R). cs 774 (Prasad) L 1 LP 9

More Queries • Constraint solving – sig: list x list -> list • append( R, [2, 3], [1, 2, 3]). – sig: list -> list x list • append(A, B, [1, 2, 3]). • Generation – sig: -> list x list • append(X, Y, Z). cs 774 (Prasad) L 1 LP 10

GCD : functional vs imperative Precondition: n > m >= 0 fun gcd(m, n) = if m=0 then n else gcd(n mod m, m); function gcd(m, n: int) : int; var pm: int; begin while m<>0 do begin pm : = m; m : = n mod m; end; return n end; cs 774 (Prasad) L 1 LP n : = pm 11

GCD: logic Precondition: n > m >= 0 gcd(M, N, N): - M = 0. gcd(M, N, G): - M = 0, M =< N, T is N mod M, gcd(T, M, G). ? -gcd(3, 4, G) G = 1; false cs 774 (Prasad) L 1 LP 12

Recursion + Logic Variables • Convenient way of defining functions over inductively defined sets (e. g. , numbers, lists, trees, etc) • Implicit Stack • No aliasing problems • Same location cannot be accessed and modified using two different names • Use semantics preserving transformations for efficiency • Role of the interpreter cs 774 (Prasad) L 1 LP 13

Progression of values bound to a variable as computation progresses • Imperative language – Essentially independent (subject to typing constraints) • Logic language – Values are in instance-of/sub-structure relation (general -> specific) cs 774 (Prasad) L 1 LP 14

OOPL: Expressive Power vs Naturalness Object-oriented techniques do not provide any new computational power that permits problems to be solved that cannot, in theory, be solved by other means (Church-Turing Hypothesis). But object-oriented techniques do make it easier and more natural to address problems in a fashion that tends to favor the management of large software projects. cs 774 (Prasad) L 1 LP 15

Other Benefits of Programming in a Declarative Language • Abstraction – Convenient to code symbolic computations and list processing applications. • Meta-programming (which exploits uniform syntax) • Automatic storage management • Improves program reliability. • Enhances programmer productivity. • Ease of prototyping using interactive development environments. • Executable Specification cs 774 (Prasad) L 1 LP 16

Logic Programming Paradigm (cont’d) cs 774 (Prasad) L 1 LP 17

Logic Program • Integrates data structures with programs • Involves asserting properties satisfied by relationships among individuals in a logic language • Computation is logical deduction – make explicit facts that are implicit, that is, are logical consequence of input cs 774 (Prasad) L 1 LP 18

Example • Prolog Facts (asserting relationships among objects) (cf. ABox) – child(c, p) holds if c is a child of p. child(tom, john). child(tom, mary). • Prolog Rules (formalizing relationships) (cf. TBox) – parent(p, c) holds if p is a parent of c. parent(P, C) : - child(C, P). cs 774 (Prasad) L 1 LP 19

Querying as Deduction ? - child(tom, john). – Is Tom a child of John? ? - child(X, john). – List children of John, one by one ? - child(X, Y). – List all child-parent pairs, one by one ? - parent(tom, X). – List children of Tom, one by one cs 774 (Prasad) L 1 LP 20

Two definitions of ancestor relation • Ancestor-relation is the reflexive transitive closure of the parent-relation. ancestor(X, X). ancestor(X, Y) : - parent(X, Y). ancestor(X, Y) : - parent(X, T), ancestor(T, Y). ancestor(X, X). ancestor(X, Y) : - parent(X, Y). ancestor(X, Y) : - ancestor(X, T), ancestor(T, Y). cs 774 (Prasad) L 1 LP 21

Prolog is not an ideal logic programming language • In traditional Prolog implementations (e. g. , SWIProlog), the query ancestor(tom, X) terminates (with correct answers), while the query ancestor(tom, X) does not terminate. • In tabled Prolog (e. g. , XSB), both queries terminate. • Left-recursion causes a depth-first search strategy to loop for ever, while both breadth-first search and tabling strategy terminate. cs 774 (Prasad) L 1 LP 22

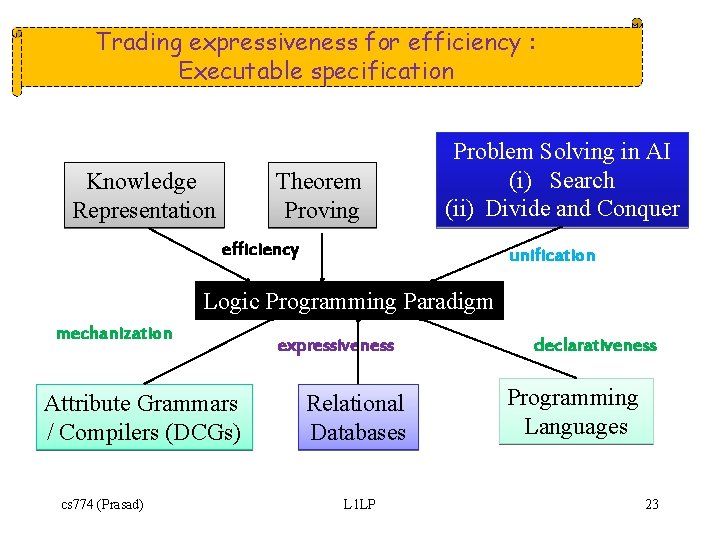
Trading expressiveness for efficiency : Executable specification Knowledge Representation Theorem Proving Problem Solving in AI (i) Search (ii) Divide and Conquer efficiency unification Logic Programming Paradigm mechanization Attribute Grammars / Compilers (DCGs) cs 774 (Prasad) expressiveness Relational Databases L 1 LP declarativeness Programming Languages 23

• Knowledge Representation – LP provides a sufficiently rich subset of firstorder logic that is computationally tractable. – Supports non-monotonic reasoning via negation -by-failure. • Deductive Databases – LP adds expressive power by extending relational query language (to support recursion) without sacrificing computational efficiency • E. g. , expression of transitive closure cs 774 (Prasad) L 1 LP 24

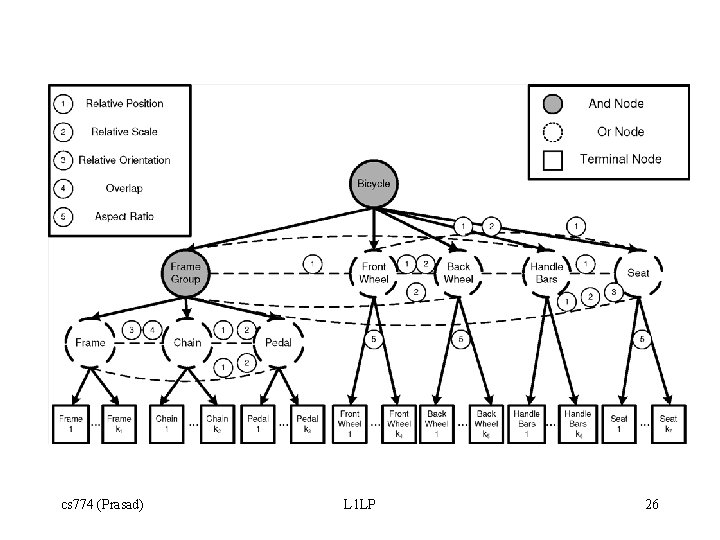
Divide and Conquer Strategy • AND-OR Graphs Goal_k : subgoal_1, subgoal_2, …, subgoal_n … subgoal_i : - Alt_i 1. subgoal_i : - Alt_i 2. … subgoal_i : - Alt_im. cs 774 (Prasad) L 1 LP 25

cs 774 (Prasad) L 1 LP 26

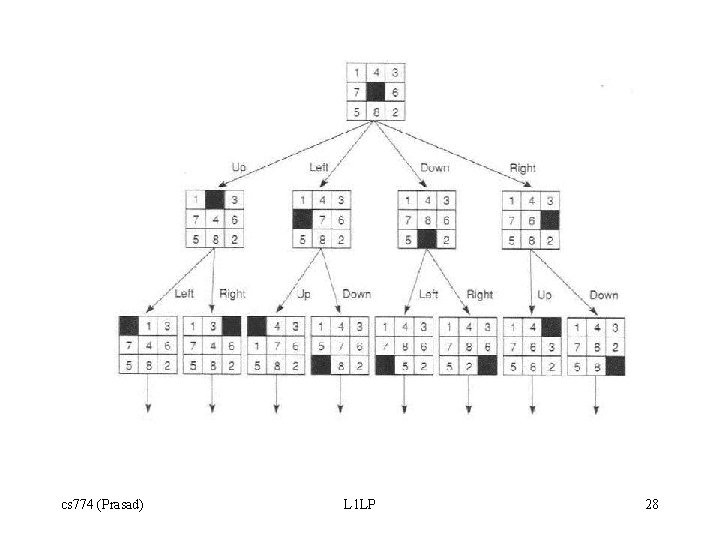
State-Space Search initial. State(_). final. States(_). … final. States(_). transitions(_, _). … transitions(_, _). solved : final. States(Y), reachable(Y) : initial. State(Y). reachable(Y) : transitions(X, Y), reachable(X). cs 774 (Prasad) L 1 LP 27

cs 774 (Prasad) L 1 LP 28

Declarative Programming permute(Lst, [Hd|Rst. Perm]): split(Hd, Lst, Rst), permute(Rst, Rst. Perm). permute([], []). split(Hd, [Hd|Tl], Tl). split(Hd, [NHd|Tl], [NHd|NTl]): split(Hd, Tl, NTl). ? - findall(X, permute([1, 2, 3], X), Xall). Xall = [[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]. cs 774 (Prasad) L 1 LP 29

Definite Clause Grammars Program abc. Lst --> abc, abc. Lst --> []. Queries ? -abc. Lst([b, c], []). true ? -abc. Lst([b, c, d], []). false abc --> [a]. abc --> [b]. abc --> [c]. cs 774 (Prasad) ? -abc. Lst([b, c, d], [d]). true L 1 LP 30