PROgramming LOGic Continued A logic programming language is

PROgramming LOGic Continued A logic programming language is a notational system for writing logical statements together with specified algorithms for implementing inference rules. 10/7/2020 Head/Lander 1

What will be covered • Lots of code 10/7/2020 Head/Lander 2

Another relation ? ? Remember "is" breaks the logical model. squares( [ ], [ ] ). squares( [N|T ], [S|ST ] ) : – S is N*N, squares( T, ST). ? – squares( [ 0, 2, 3, 1], X ). X = [ 0, 4, 9, 1] ? – squares( [ ], X ). X=[] ? – squares( [2, 4, 6], [4, 16, 36] ). yes 10/7/2020 Head/Lander 3

More simple examples • Counts all the positive numbers in a list. (i. e. n >0) Your solution should allow only one correct solutions. positive( List, Number. Of. Pos). • Partition a list of numbers into a positive list and a negative list. selectpn( List, Positive. List, Neg. List ) 10/7/2020 Head/Lander 4

positive( [ ], 0). positive( [ H | T ], Z ) : – H > 0, !, positive( T, Z 1 ), Z is 1 + Z 1. positive( [ _ | T ] , Z ) : – positive( T, Z ). ? – positive( [ 0, – 1, – 5, 5], X ). X=1 ? – positive( [1, – 2, 4, 2, 3], X ). X=4 ? – positive( [ ], X ). X=0 10/7/2020 Head/Lander 5

selectpn( [ ], [ ] ). selectpn( [ 0 | T ], X, Y ) : – selectpn( T, X, Y ), !. selectpn( [ H | T ], [ H|Z ], X ) : – H > 0, !, selectpn ( T, Z, X ). selectpn( [ H | T ], X, [ H|Z ] ) : – selectpn ( T, X, Z ). ? – selectpn( [ 0, – 1, – 5, 5], X, Y ). X = [5] Y = [– 1, – 5] ? – selectpn( [1, – 2, 4, 2, 3], X, Y ). X = [1, 4, 2, 3] Y = [– 2] 10/7/2020 Head/Lander 6

permute( [ ], [ ] ). permute(L, [ X | Y ] ) : – select( L, X, T ), permute( T, Y ). select( [ X | Y ], X, Y ). select( [ X | Y ], Z, [ X | T ] ) : – select( Y, Z, T). ? – permute( [ 1, 4, 7 ], X ). X = [ 1, 4, 7 ]; X = [ 1, 7, 4 ]; X = [ 4, 1, 7 ]; X = [ 4, 7, 1 ]; X = [ 7, 1, 4 ]; X = [ 7, 4, 1 ]; no 10/7/2020 Head/Lander 7

Try: callperm( X ): – permute( X , Y ), write(Y ), nl, fail. ? – callperm( [1, 4, 7] ). [1, 4, 7] [1, 7, 4] [4, 1, 7] [4, 7, 1] [7, 1, 4] [7, 4, 1] no 10/7/2020 Head/Lander 8

Recursion revisited fibonacci_1( X , 1) : – X =< 2. fibonacci_1( X , Y ) : – X > 2, X 1 is X – 1, X 2 is X – 2, fibonacci_1( X 1, Y 1), fibonacci_1( X 2, Y 2), Y is Y 1 + Y 2. 10/7/2020 Head/Lander 9

Improvement: Memoization Using asserta to add facts to our program. (Need directive : -dynamic) fibonacci_2( 1, 1). fibonacci_2( 2, 1). fibonacci_2( X, Y ) : – X > 2, X 1 is X – 1, X 2 is X – 2, fibonacci_2( X 1, Y 1 ), fibonacci_2( X 2, Y 2 ), Y is Y 1 + Y 2, asserta(fibonacci_2( X, Y )). 10/7/2020 Head/Lander 10

Dynamic Programming USING STATE VARIABLES (ACCUMULATORS) TO PASS VALUES FROM ONE ITERATION TO THE NEXT. (How would you simulate an array in Prolog? ) fibonacci_3( N, Fib): – fib_aux( 2, N, 1, 1, Fib ). fib_aux ( N, N, F 1, Fib ). fib_aux ( M, N, F 1, F 2, F ) : – M < N, Next. M is M + 1, Next. F 2 is F 1 + F 2, fib_aux(Next. M, N, F 2, Next. F 2, F). 10/7/2020 Head/Lander 11

Breaking the model • Another break of the logical model. . . – Problems that can occur depending on the position of Variables in a predicate – Problems that can occur depending on the order of the predicates in a Query • The problem with NOT 10/7/2020 Head/Lander 12

% Assume family. pl parent( X , Y ) : – mother( X , Y ). /* If mother( X , Y ) then parent( X , Y ) */ parent( X , Y ) : – father( X , Y ). grandparent( X , Z ) : – parent( X , Y ), parent(Y, Z ). mother(mary, ann). mother(mary, joe). mother(sue, mar. Y ). father(mike, ann). father(mike, joe). grandparent(sue, ann). /* Redundant */ sibling( X , Y ) : – parent(P, X ), parent(P, Y ). ? - sibling( X, Y ). X = ann Y = ann 10/7/2020 Head/Lander 13

sibling( X , Y ) : – parent(P, X ), parent(P, Y ), not( X = Y). both-parent-sibling( X , Y ) : – mother( M, X ), mother( M, Y ), father( F, X ), father( F, Y ), not( X = Y ). 1? - sibling( X, Y ). X = ann Y= joe 2? - both-parent-sibling( X , ann). X = joe 10/7/2020 Head/Lander 14

Negation: not(P) : – call(P), !, fail. not(P). alternatively: not(P): – P, !, fail; true. alternatively: not(P): – P, !, fail. not(P): -true. 10/7/2020 Head/Lander 15

The trouble with “not” test( S, T) : - S = T. 1? - test( 3, 5). no 2? - test( 5, 5). yes 3? - not( test( 5, 5)). no 4? - test( X, 3), R is X+2. X=3 R=5 5? - not( test( X, 3))), R is X+2. warning unbounded variable in arithmetic expression fail. . . /* When not(test(X, 3)) fails the instantiation of X to 3 is released */ 10/7/2020 Head/Lander 16

Another problem with not /* X instantiated to 0, then not( 0= 1) succeeds. */ 6? - X = 0, not( X=1). X=0 /* X instantiated to 1, not( X=1) fails, the goal X = 0 is never reached */ 7? - not( X=1 ), X=0. no 10/7/2020 Head/Lander 17

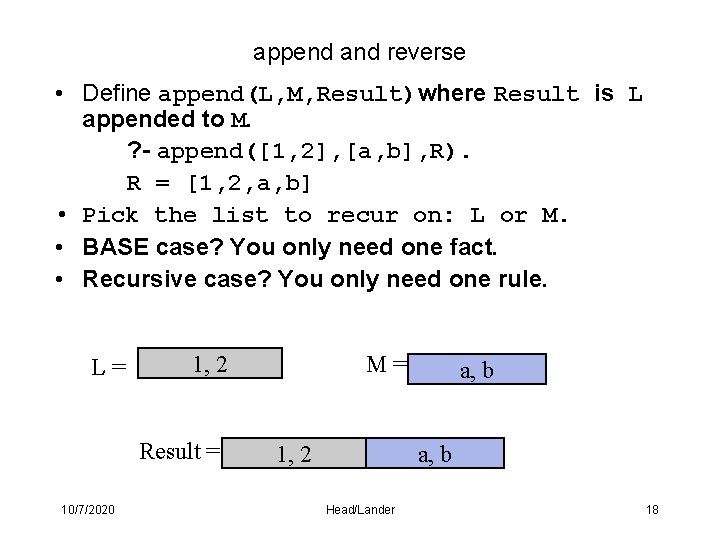
append and reverse • Define append(L, M, Result)where Result is L appended to M. ? - append([1, 2], [a, b], R). R = [1, 2, a, b] • Pick the list to recur on: L or M. • BASE case? You only need one fact. • Recursive case? You only need one rule. L= 1, 2 Result = 10/7/2020 M= 1, 2 a, b Head/Lander 18

append continued • Using append to retrieve the prefix, suffix of a list append(Prefix, [e, e|Suffix], [a, b, c, d, e, e, f, g]). • Partitioning a list around an element. -- delete append (Before, [d|After], [a, b, c, d, e, e, f, g]). • Another definition of member( E, L) : - append( L 1, [E|L 2], L). • What is big "O" of append? 10/7/2020 Head/Lander 19

Reversing a list • Naive code using append. • Examine the recursion -- work done during the return. • Using a "helper" functor to have the work done before the call. • Faster 10/7/2020 Head/Lander 20

Reverse- Slow rev([ ], [ ]). rev([Head|Tail], Result) : - rev(Tail, Reversed. Tail), append(Reversed. Tail, [Head], Result). • Without cuts ? - rev(X, [a, b]) goes into a loop after “; ” 10/7/2020 Head/Lander 21

Reverse-Slow rev. A([ ], [ ]). rev. A([Head|Tail], Result) : append(Reversed. Tail, [Head], Result), rev. A(Tail, Reversed. Tail). • Without cuts ? - rev. A([a, b], X) goes into a loop after “; ” 10/7/2020 Head/Lander 22

Reverse--Fast rev. Eff(List, RList) : - rev. Eff(List, [ ], RList). % Helper -- t. r. rev. Eff([ ], RL). rev. Eff([Element|List], Rev. Prefix, RL) : rev. Eff(List, [Element|Rev. Prefix], RL). • Without cuts ? - rev. Eff(X, [a, b]) goes into a loop after “; ” 10/7/2020 Head/Lander 23

Difference lists • Represent a list segment as a list-pairs, separated by any symbol, typically the “-” sign • The second of the pair is the later part of the first list: [a, b| X] - X where L = [a, b | X] (L - X) L X L [a, b | X] a b 10/7/2020 Head/Lander 24

• The “difference” is interpreted (by the reader ) as a list containing only the first part of the first of the pair; up to the beginning of the second list in the pair: [a, b, c, d | X] - [c, d | X] is interpreted as [a, b] • In fact, one of the best forms to work with is: [a, b, c, d | X ] - X which is interpreted as [a, b, c, d] 10/7/2020 Head/Lander 25

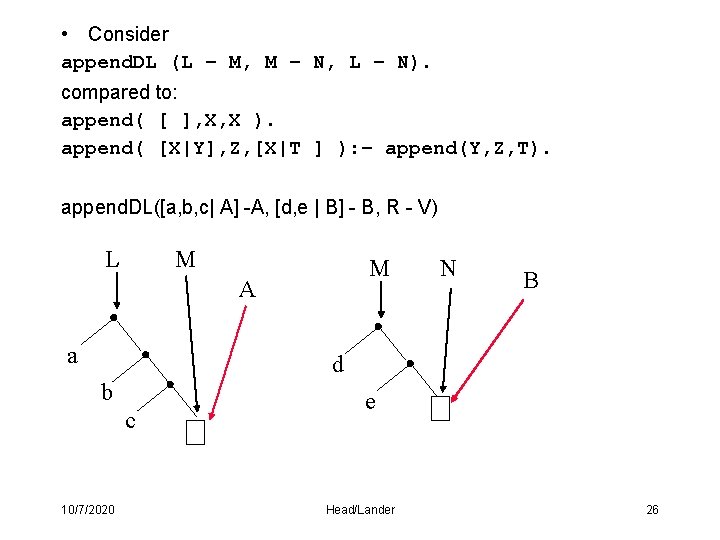
• Consider append. DL (L – M, M – N, L – N). compared to: append( [ ], X, X ). append( [X|Y], Z, [X|T ] ): – append(Y, Z, T). append. DL([a, b, c| A] -A, [d, e | B] - B, R - V) L M M A a N B d b c 10/7/2020 e Head/Lander 26

append. DL([a, b, c|A] -A, [d, e |B] - B, R - V). append. DL (L – M, M – N, L – N). L R M a M V d b e c 10/7/2020 N Head/Lander 27

append. DL (L – M, M – N, L – N). 1? –append. DL( [1, 2, 3|X]-X, [4, 5]-[ ], Y – Z ). X = [4, 5] Y = [1, 2, 3, 4, 5] Z = [ ] 2? –append. DL( [1, 2, 3|X]-X, [4, 5|Y]-Y, W–Z ). X = [4, 5| _n] Y = _n W = [1, 2, 3, 4, 5| _n] Z = _n 10/7/2020 Head/Lander 28

Converting a Difference List to a list: simplify( X -Y, [] ): - X == Y. simplify( [X|Y]-Z, [X|W] ): simplify(Y-Z, W). ? -simplify( [1, 2, 3|X]-X, Y ). Y = [1, 2, 3] 10/7/2020 Head/Lander 29

Quick sort is very intuitive in Prolog: qsort( [P|L], Outlist): – partition( P , L, Small, Large), qsort(Small, Localsmall), qsort(Large, Locallarge), append(Localsmall, [P|Locallarge], Outlist). qsort( [ ], [ ] ). partition( _, [ ], [ ] ). partition( P , [Y|T], [Y|Sml], Lg) : – P > Y, !, partition(P, T, Sml, Lg). partition( P , [Y|T], Sml, [Y|Lg] ): – partition(P, T, Sml, Lg). 10/7/2020 Head/Lander 30

Quick. Sort using Difference Lists qsort 1(Inlist, Outlist): – qsort 2(Inlist, Outlist – [ ] ). qsort 2( [X|Tl], A 1–Z 2): – partition( X , Tl, Sm, Lg), qsort 1(Sm, A 1–[X|A 2] ), qsort 1(Lg, A 2–Z 2). qsort 2( [ ], Z–Z ). 10/7/2020 Head/Lander 31

Grammars and Prolog • Prolog is use in artificial intelligent processing especially for natural language processing. • Recognizers are easy to program in Prolog given a BNF grammar. • Converting the BNF grammar for anbn S -> a b | a S b where S is a non-terminal symbol and a, b terminal symbol s --> [a], [b]. s --> [a], s, [b]. where "[]" are used for terminal symbols and atoms for nonterminal symbols. Replace -> with -->, S with s and a, b with [a], [b] 10/7/2020 Head/Lander 32

Under the Covers • • s --> [a], [b]. s --> [a], s, [b]. Is syntactic sugar for s(A, B) : - 'C'(A, a, C), 'C'(C, b, B). s(A, B) : - 'C'(A, a, C), s(C, D), 'C'(D, b, B). 'C'([A|B], A, B). Notice that 'C' is an atom and C is a variable We represent the language as a list of a & b atoms. To check if a string is recognized enter the following query: s([a, a, a, b, b, b], []). s([a, a, b, b, ], []). 10/7/2020 Head/Lander 33

Be careful with the Grammar • • Because of the way Prolog executes it is a top down parser. It behaviors like a recursive decent parser. Left recursion must be removed to avoid "stack overflow". So the grammar for balance "()" s -> ( ) | ( s ) | s s can not be used • However it can be transformed to : s -> ( ) | ( ) s | ( s ) s 10/7/2020 Head/Lander 34

Additional Examples-- may not be discussed • • • Sum of Subset Towers of Hanoi puzzle Recursive data structures - trees looping -- generate and test Implementing repeat loop in Prolog Implementing for loop in Prolog 10/7/2020 Head/Lander 35

Naturally solved Problems using Prolog • Logic programming is a natural choice for problems that fit the database model and for algorithms that require the built-in backtracking search capability of logic programming. • Sum of subset decision problem. – What is the problem? – What is the code? • sum. Ofsubset(Set, Sum, Sub. Set). • What is the fact? • What are the rules? 10/7/2020 Head/Lander 36

Sum of Subsets • Problem: Given n positive integers w 1, . . . wn and a positive integer W. Find all subsets of w 1, . . . wn that sum to W. – Similar to the 0 -1 knapsack problem. When the benefit of each item is equal to its weight the 0/1 Knapsack problem becomes the sum of subsets problem. • Example: n=3, W=6, and w 1=2, w 2=4, w 3=6 • Solutions: {2, 4} and {6} 10/7/2020 Head/Lander 37

Sum of subsets • We will assume a binary state space tree. • The nodes at level 1 are for including (yes, no) item 1, the nodes at level 2 are for item 2, etc. • The left branch includes wi, and the right branch excludes wi. • The nodes contain the weights included so far 10/7/2020 Head/Lander 38

Sum of subset Problem: State Space. Tree for 3 items w 1 = 2, w 2 = 4, w 3 = 6 and W = 6 0 yes i 1 2 0 6 i 2 yes 12 yes no yes i 3 no 4 2 no 6 yes 8 no no 2 yes 10 0 no 4 yes 6 no 0 The total weight up to the node is stored at the node. 10/7/2020 Head/Lander 39

• Towers of Hanoi puzzle: hanoi(N): – move(N, left, right, center). move(0, _ , _ ) : – !. move(N, A, B, C): – M is N– 1, move(M, A, C, B), inform(A, B), move(M, C, B, A). inform(X, Y): –write([move, a, disc, X, to, Y]), nl. ? -hanoi(3). move a disc move a disc 10/7/2020 left to right left to center right to center left to right center to left center to right left to right Head/Lander 40

Recursive "data" structure: Representing Binary Trees Binary tree structure: node(Self, Leftsubtree, Rightsubtree). binarytree(empty ). binarytree(node ( X , Y, Z )): – binarytree (Y ), binarytree (Z ). 10/7/2020 Head/Lander 41

Searching the binary tree structure tree. Member (E, node (E, _ )): – !. /* cut off search after first time the element is found */ tree. Member(E, node ( N , L, _ )): – E < N, !, tree. Member (E, L). /* cut if E < N to avoid searching the right subtree */ tree. Member(E, node ( _ , R )): –tree. Member(E, R). 10/7/2020 Head/Lander 42

Repetition: Generate and test natural(1). natural(N) : - natural(M), N is M+1. loop(N) : -natural(Int), Int =< N, write(Int), nl, Int=N, !. 10/7/2020 Head/Lander 43

Repetition Through Backtracking Built-in: repeat : - repeat. % repeat turns any predicate into a generator % Infinite number of “*” stars : - repeat, write(‘*’), fail. % repeat until “end of line” key. Board : - repeat, get 0(C), C = 0, !. 10/7/2020 Head/Lander 44

Limitations of Repeat • Prolog’s repeat is quite different than a procedural language’s repeat because backtracking can take any subgoal that has an untried alternative. • The only way to pass information from one pass to another is to use assert to store data in the knowledge base. 10/7/2020 Head/Lander 45

Repetition Through Backtracking for loop: for Index = Start to Finish for(I, I, I) : - !. for(I, I, _). for(Index, S, F) : - %R 1 %R 2 N is S+1, for(Index, N, F). %R 3 printint(S, F) : - for(Ind, S, F), write(Ind), nl, fail. 10/7/2020 Head/Louden p 457 ex 32 46

% For. Loop: for(I, I, I) : - !. for(I, I, _). for(Index, S, F): - N is S+1, for(Index, N, F). printint(S, F): -for(Ind, S, F), write(Ind), nl, fail. ? - for(I, -1, 2). I = -1 ; I = 0 ; I = 1 ; I = 2 ; No ? 10/7/2020 Head/Lander 47

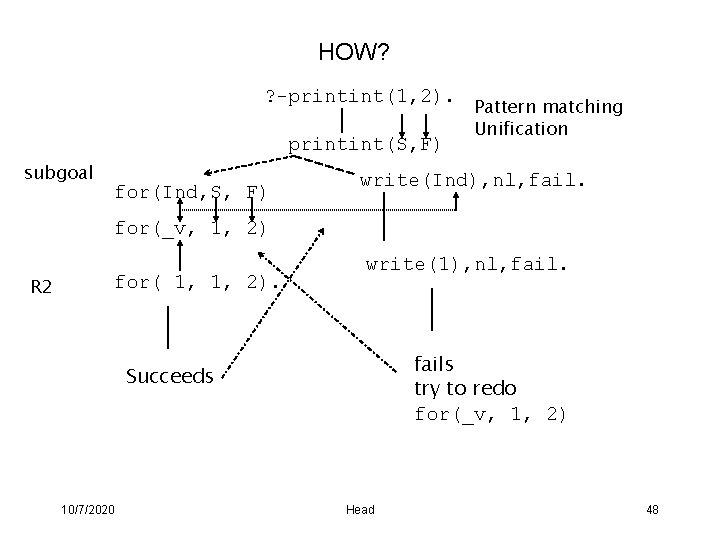
HOW? ? -printint(1, 2). printint(S, F) subgoal for(Ind, S, F) Pattern matching Unification write(Ind), nl, fail. for(_v, 1, 2) R 2 for( 1, 1, 2). write(1), nl, fails try to redo for(_v, 1, 2) Succeeds 10/7/2020 Head 48

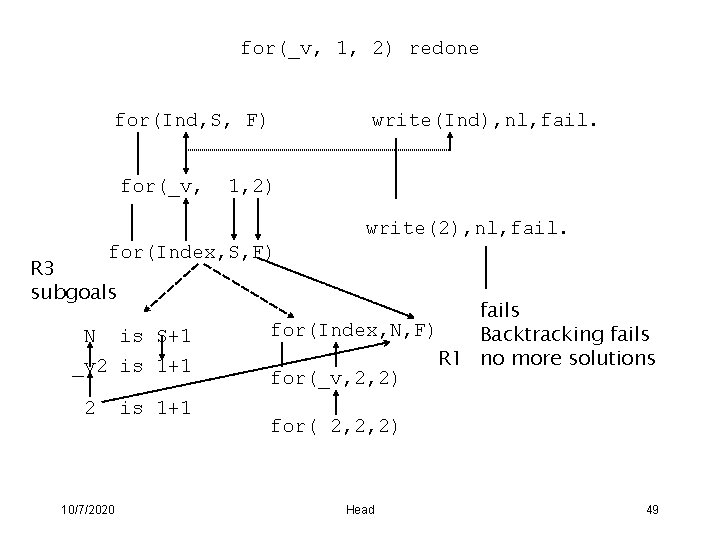
for(_v, 1, 2) redone for(Ind, S, F) for(_v, write(Ind), nl, fail. 1, 2) write(2), nl, fail. for(Index, S, F) R 3 subgoals N is S+1 _v 2 is 1+1 2 10/7/2020 is 1+1 fails for(Index, N, F) Backtracking fails R 1 no more solutions for(_v, 2, 2) for( 2, 2, 2) Head 49