Programming Languages for Compressing Graphics Morgan Mc Guire

Programming Languages for Compressing Graphics Morgan Mc. Guire Shriram Krishnamurthi John F. Hughes Brown University { morgan | sk | jfh}@cs. brown. edu

Encoding Images as Programs

Describing Images (1) set. Pixel(0, 0, BLUE); set. Pixel(1, 0, BLUE); set. Pixel(2, 0, BLUE); … set. Pixel(50, 0, WHITE); … set. Pixel(100, 0, RED); set. Pixel(101, 0, RED); …

The Cost of Bandwidth n Major cost of doing business on the web n n n Yahoo!: 65, 000 pages/day Valve: 1 M €/software patch Image compression is a one-shot activity Low vs. high bandwidth users Multiresolution

Describing Images (2) repeat 50 times next. Row(); repeat 50 times … set. Next. Pixel(BLUE); set. Next. Pixel(WHITE); set. Next. Pixel(RED); set. Next. Pixel(BLUE);

American Flag Doesn’t compress as well as the French flag in the “repeat n times” language.

Adding More Primitives draw. Rectangle(BLUE, …); draw. Rectangle(RED, …); draw. Rectangle(WHITE, …); draw. Star(WHITE, …); … Is this enough?

Describing Complex Images

Describing Complex Images n n n JPEG: language consists of frequency domain instructions GIF: language consists of set. Pixel and dictionary lookup Preferred format depends on the image

Observations n n Images are programs Even within one language, many possible descriptions produce similar images n n n Lossy compression Description length depends on language and image complexity Best compression when the language matches the image

The Obvious Compression Scheme n Compress the image in several formats n n n TGA, GIF, JPG, SVG, SWF Choose the best Add a byte to the front of the file specifying the compression language

Problems with the Obvious Scheme n n n None of the formats may be particularly good for our image Even JPEG tops out around 50: 1, has serious artifacts Lacking ideal features like: n n n Multiresolution Time/Space tradeoff Introduction of new formats requires new browser plug-ins

Describing Complex Images How can we do better than the obvious approach for images like this?

Using an Expressive Language (compose (vertical-gradient BLUE WHITE) (polygon DARK-BLUE …) (polygon BLACK …) (* (polygon …) (blur tree-texture) YELLOW))

Using an Expressive Language n n What if we design a really expressive language for representing images? Because the “data” is a program the decompressor is part of the “data” n n Each image gets its own custom format High compression We have control over multiresolution, perceptual artifacts Package for the web as a plug-in n We only need to upgrade the plug-in when the language itself changes What’s wrong with this plan?

Example set. Pixel Language Expressive Language set. Pixel(0, 0, WHITE); ? (blur (+ set. Pixel(1, 0, WHITE); (rotate (banana)) set. Pixel(2, 0, WHITE); (distort (* RED … 2 Mb (circle))) …) 2 kb

The Encoding Problem ? Pierre can’t code!

The Encoding Problem Photoshop menu set. Pixel(0, 0, WHITE); EMACS (blur (+ set. Pixel(1, 0, WHITE); (rotate (banana)) set. Pixel(2, 0, WHITE); (distort (* RED … 2 Mb (circle))) …) 2 kb

Where is the “Save as Code” Menu? n n n It is easy to convert from an image to programs in the GIF/JPG language More expressive language = harder conversion How much harder?

Much Harder! n n n Converting the image into a program that produces it is a search problem The search space is the space of all possible programs This is an infinitely large space

Tempering Expressiveness “Good” compression languages are ones where: n Expressive power is large n Searching is easy How do we make searching easy?

Steerable Search Techniques n Genetic Algorithms n n Metropolis Search n n Inject domain information through fitness function Inject domain information through transition probabilities Simulated Annealing n Inject domain information through gradient estimation

Perceptual Fitness Function e (i ) = edge filter, b (i ) = convolve with Gaussian, |ix | = color magnitude n n Tweaking this is the domain-expert’s job Perfect fitness function not necessary (or possible!)

Designing the Language n Desirable language properties for compression n Expresses many images compactly There are many programs for which another, shorter program exists that produces visually similar output Desirable search properties n n Mutations safety All programs terminate

The Evolver Language Scalar : = real between 0 and 1 Vector : = Scalar x Scalar Matrix : = Vector* Value : = Matrix | Scalar | Vector Operator : = Add | Collage | Blur | Noise | … Call : = Operator x Expr* Expr : = Call | Scalar | Vector

The Evolver Language n n n Automatic coercion between Matrix, Vector, Scalar Every operator has the same domain and range Primitives include stock images and textures No looping constructs No functions!

l: Not the Ultimate Compressor!

l: Not the Ultimate Compressor! n Copying code is sometimes good n n Multiple instances of a pattern in an image often differ slightly Hard to evolve both definition and multiple applications

Added Benefits of Search n n Artist can save the image immediately Webmaster uses Evolver toolkit to search for an equivalent program n n n It is easy to find a large program quickly Webmaster lets Evolver continue to run Upload new, smaller encodings as they are found More time = less space = less cost Multiple constraints: size, time, artifacts, decompression time

Results

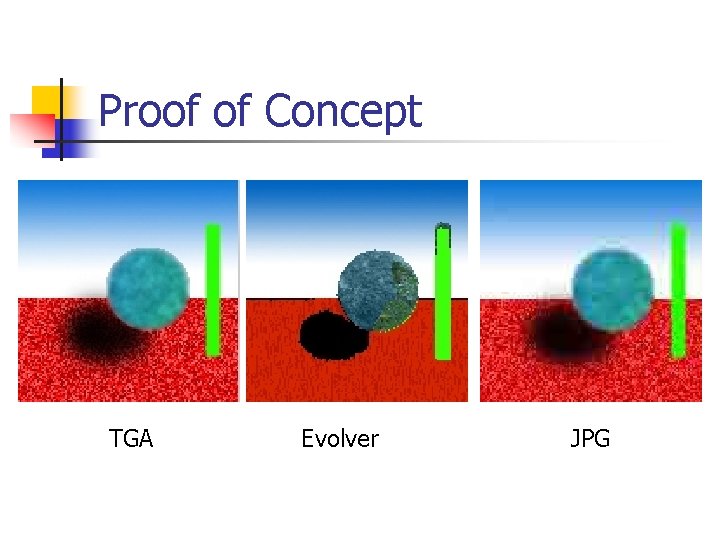
Proof of Concept TGA 1: 1 (128 x 128)

Proof of Concept JPG 24: 1 (64 x 64)

Proof of Concept Evolver 50: 1, infinite detail resolution

Proof of Concept TGA Evolver JPG

Lake Matheson Original

Lake Matheson Original Compressed 50: 1

Gradient Original Compressed

Aspens Original

Aspens Original Compressed 54: 1

Maples Original

Maples Code Collage(Hue. Shift(Min(Rock. Image(), Collage(Rotate(0. 22693111, {0. 4339271, -0. 060890462, -0. 14983156}), {0. 9689341, -0. 31166452, 1. 0}, Environment. Map(Interpolate(Derivative({0. 5260445, -0. 9943271, -0. 83629435}), Fish. Image(), 0. 22693111), Collage(VSplit(VGradient(), Interpolate(Min(Rock. Image(), Collage(0. 22693111, {0. 90638816, 0. 3161332, 1. 0}, Environment. Map({0. 3538252, -0. 11179591, 0. 76402247}, {0. 3538252, -0. 11179591, 0. 76402247}))), 0. 75621074, Derivative(Hue. Shift(Low. Color. Noise(), {-0. 60136193, -0. 9961748, 0. 956824})))), {-0. 6025814, -0. 5151359, 0. 2444776}, Mini. Blur({0. 48381335, 0. 37744927, 0. 18049468})))))), Leaf. Image()), Rotate(Interpolate(Max(Rotate(Leaf. Image(), Cosine({0. 13357106, -0. 48899084, 0. 46273336})), Leaf. Image()), {0. 26036343, -0. 2474052, 0. 3318561}, Add(Rotate(Interpolate(Max(Low. Noise(), Leaf. Image()), {0. 26036343, -0. 2474052, 0. 3318561}, Add(Rotate(Interpolate({0. 26036343, -0. 2474052, 0. 3318561}, Max(Rotate(Blur(Noise()), Frequency. Stars()), Bit. And(VSplit(Leaf. Image(), {-0. 3782095, 0. 06973941, 0. 7708523}), Collage(Blur({0. 19214037, 0. 7060751, 0. 9632803}), {-0. 94875985, 0. 9535051, 0. 9628181})))), Frequency. Stars()), Zoom({0. 84155905, 0. 44450688, -0. 6368634}, Interpolate(0. 97325927, {0. 43938103, 0. 8003519, -0. 8865588}, Frequency. Stars())))), Frequency. Stars()), Zoom({1. 0, 0. 35874906, -0. 42753658}, {1. 0, 0. 35874906, -0. 42753658}))), Frequency. Stars()), {0. 30287892, -0. 7879979, 0. 756324}), Distort(Distort(Hue. Shift(Distort(Rotate(Distort(Hue. Shift(Distort(Rotate(Distort(Distor t(Blur(Distort(Rock. Image(), Arc. Tangent(Expand. Range(Color. Noise())))), Arc. Tangent(Expand. Range(Color. Noise()))), Arc. Tangent(Color. Noise())), Rock. Image()), Color. Noise()), Blur(Add({0. 214469, -0. 05106278, -0. 8334819}, Blur({-0. 44914088, 0. 86714524, -0. 038012877}))))), Distort(Blur(Distort(-0. 32682085, Sunrise. Image()), Arc. Tangent(0. 84263784))), Leaf. Image()), Arc. Tangent(Color. Noise())), Expand. Range(Rock. Image())), 0. 315652), Color. Noise()), Blur(Expand. Range(Add({0. 44753784, 0. 15750253, -0. 9017423}, {0. 214469, -0. 05106278, -0. 8334819})))), Expand. Range(Rock. Image())), Color. Noise()), Blur(Rotate({0. 10588625, 0. 2359776, -0. 20337643}, {0. 2809281, -0. 97692156, -0. 49766022}))))

Maples Original Compressed 56: 1

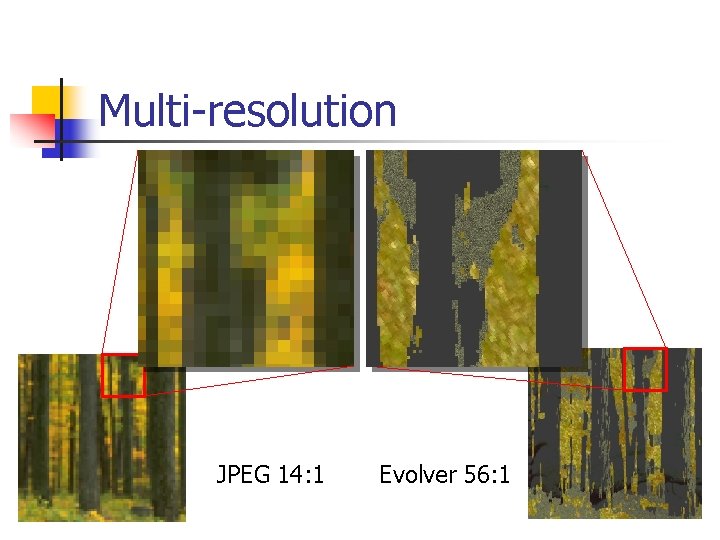
Multi-resolution JPEG 14: 1 Evolver 56: 1

Multi-resolution JPEG 14: 1 Evolver 56: 1

Related work n Searching for programs n n n Palsberg, Lucier & Mamillapalli Karl Sims Programmatic image compression n Massalin’s Superoptimizer Frigo & Johnson’s FFTW Fractal compression MPEG-7 Steerable search techniques in graphics n n MLT Radiosity

Conclusions n n n It is tractable to search the space of all programs! The “visually similar” criterion makes computer graphics an interesting domain Keep using JPEG for now…

Future directions n n Improve image quality/compression How can the design of searchable languages be formalized? How do expressive constructs affect the search problem? Other interesting domains: animation, audio compression, image search, robot controllers

Questions http: //www. cs. brown. edu/people/morgan/evolver