Programming Interest Group http www comp hkbu edu

Programming Interest Group http: //www. comp. hkbu. edu. hk/~chxw/pig/index. htm Tutorial Six Divide and Conquer and Backtracking 1

Outline l l l Recursion Divide and Conquer Backtracking l Examples l l l Constructing all subsets Constructing all permutations Pruning l Eight-Queens Problem 2

Recursion l A recursive function is one that calls itself. l l There must be a termination condition. Example: l l Factorial function N! = Nx(N-1)x(N-2)x…x 2 x 1. 0! = 1 int factorial (unsigned int N) { if (N == 0) return 1; return N*factorial(N-1); } 3

Example: Euclid’s Algorithm l Find the greatest common divisors of two integers gcd(314159, 271828) int gcd (int m, int n) { if (n == 0) return m; return gcd(n, m%n); } gcd(271828, 42331) gcd(42331, 17842) gcd(17842, 6647) gcd(6647, 4458) gcd(4458, 2099) gcd(2099, 350) gcd(350, 349) gcd(349, 1) gcd(1, 0) return 1; 4

Recursive Functions l Advantage: l l l Allow us to express complex algorithms in a compact form Recursive functions are the cornerstone of several advanced techniques: backtracking, divide and conquer, dynamic programming Disadvantage: l l l We are nesting function calls Overhead of function calls Sometimes the program will fail because of the depth of recursion is too large! 5

Fibonacci Number l l l Fn = Fn-1 + Fn-2; F 0 = 0; F 1 = 1 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … How about writing a recursive function? int fib( unsigned int n ) { if (n == 0 || n == 1) return n; Can you figure out the drawback of the left algorithm? return fib(n-1) + fib(n-2); } 6

Divide and Conquer l Divide-and-conquer is a common and important strategy in problem-solving. l l l Divide: to split the problem into two roughly equal subproblems, which are then solved recursively. Conquer: to patch together the two solutions of the subproblems, perform a small amount of additional work, and arrive at a solution for the whole problem For divide-and-conquer approach, the sub-problems should be independent. l Fibonacci number problem cannot be solved by divide-andconquer: Fn = Fn-1 + Fn-2 7

Divide and Conquer l Example: find the maximum among N items stored in an array a[0], …, a[N-1] // a common and simple solution for (t = a[0], i=1; i < N; i++) if (a[i] > t) t = a[i]; It’s used to show the concept. Its performance is not as good as the left one. // divide and conquer int max( int a[], int l, int r ) { int m, u, v; if (l == r) return a[l]; m = (l+r)/2; u = max(a, l, m); v = max(a, m+1, r); if (u > v) return u; else return v; } 8

Divide and Conquer l Example: Fast Exponentiation l Calculate XN where N is an unsigned integer int Exp( int x, unsigned int n ) { int temp; if (n == 0) return 1; if (n == 1) return x; if (n % 2 == 0) { temp = Exp(x, n/2); return temp * temp; } else { temp = Exp(x, n/2); return temp * x; } } 9

Divide and Conquer l l Example: binary search Task: search an item in a sorted array Binary. Search(int A[], int value, int low, int high) { int mid; if (high < low) return -1; // not found mid = (low + high) / 2; if (A[mid] > value) return Binary. Search(A, value, low, mid-1); else if (A[mid] < value) return Binary. Search(A, value, mid+1, high); else return mid; // found } 10

Divide and Conquer l Example: Mergesort l l A stable sorting algorithm with worst-case running time of O(Nlog. N) Algorithm: l l l Divide the list into two sub-lists Sort each sub-list (recursion) Merge the two sorted sub-lists 11

Mergesort void msort(int A[], int temp[], int left, int right) { int mid; if (left < right) { mid = (left + right) / 2; msort(A, temp, left, mid); msort(A, temp, mid+1, right); merge(A, temp, left, mid+1, right); } } void mergesort(int A[], int N) { int *temp = malloc(N * sizeof(int)); if (temp != NULL) { msort(A, temp, 0, N-1); free(temp); } } O(N) 12

Backtracking l Backtracking is a systematic method to iterate through all the possible configurations of a search space. Traversal using right-hand rule 13 Ref: http: //en. wikipedia. org/wiki/Maze

Backtracking l l l Given a problem, it may have a large number of different possible solutions, called “search space”, and your task is to find one correct solution or all correct solutions. Brute force strategy: go through all possible solutions, and check them one by one Today’s CPU (e. g. , 3 x 109 Hz) should be able to handle the problems with search space size of millions to billions. 14

Backtracking l l Size of search space is usually related to the number of variables of the problem and the possible values of each variable E. g. , given 20 variables, each one can be either 0 or 1, then we have 220 different candidate solutions, which is around 1 million (106) E. g. , given 12 variables, each one can be 0, 1, 2, …, 9, then we have 1012 different candidate solutions! --- brute force may not be a good idea for ACM contest E. g. , given 12 variables, which are the permutation of 1, 2, 3, …, 12, then we have 12! = 479, 001, 600 different candidate solutions. Brute force may work! 15

Backtracking l How to iterate through all the possible configurations of a search space? l l l Recursion is the answer Assume the problem has n variables, stored as a vector a = (a 1, a 2, …, an), and each variable ai is selected from a finite ordered set Si. Backtracking: 1. 2. 3. Process a partial solution (a 1, a 2, …, ak). If k == n, it is a complete solution and we should handle it. Otherwise, goto Step 2. Add one more variable ak+1, find the candidates for ak+1, i. e. , Sk+1. For each possible value of ak+1, process (a 1, a 2, …, ak+1) by recursion 16

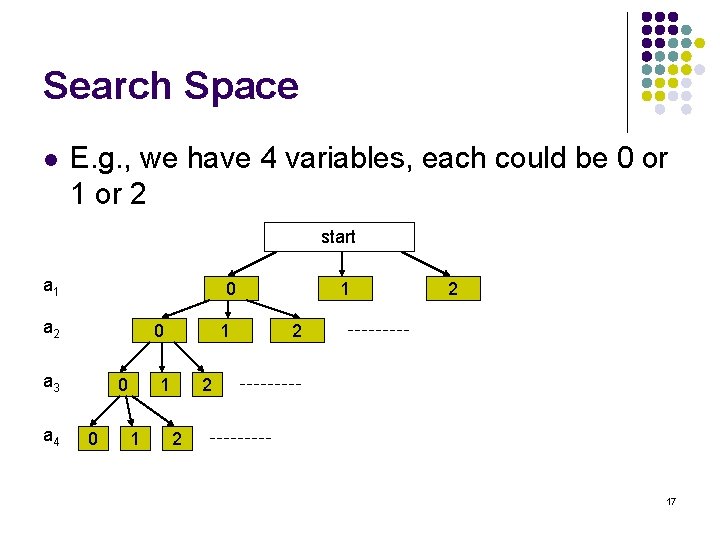
Search Space l E. g. , we have 4 variables, each could be 0 or 1 or 2 start a 1 0 a 2 0 a 3 a 4 0 0 1 1 2 2 17

Backtracking l A general programming structure bool finished = FALSE; /* to control when to stop */ backtrack(int a[], int k, data input ) { int candidate[MAX]; /* candidates for next variable */ int ncandidates; /* number of candidates for next variable */ int i; if ( is_a_solution(a, k, input) ) process_solution(a, k, input); else { k++; construct_candidates(a, k, input, candidate, &ncandidates); for (i = 0; i < ncandidates; i++) { a[k] = candidate[i]; backtrack(a, k, input); if (finished) return; /* we can terminate early by setting flag finished */ } } } 18

Some Comments l is_a_solution(a, k, input) l l l construct_candidates(a, k, input, c, ncandidates) l l l Test whether the first k elements of vector a are a complete solution for the given problem Argument input allows to pass general information into the routine, e. g. , the size of a target solution. It could be ignored in some cases. Fill an array c with the complete set of possible candidates for the kth position of a, given the contents of the first k-1 positions. The number of candidates returned is denoted by ncandidates process_solution(a, k) l Process a complete solution once it is constructed 19

Example 1: Constructing All Subsets l l Given a set with n items, we have 2 n subsets. How to output all the subsets? E. g. , the subsets of {1, 2, 3} include l l l l {123} {12} {13} {1} {23} {2} {3} {} Introduce three variables, a 1, a 2, a 3. Each of them can be either true or false. ai is true means that i is in the subset. 20

Constructing All Subsets is_a_solution(int a[], int k, int n) { return (k == n); } process_solution(int a[], int k, int n) { int i; printf(“{ “); for(i = 1; i <= k; i++) { if (a[i] == TRUE) printf(“ %d”, i); printf(“ }n”); } Reminder: In this example, the first variable is a[1]. a[0] is not used! 21

Constructing All Subsets construct_candidates(int a[], int k, int input, int c[], int *n) { c[0] = TRUE; c[1] = FALSE; *n = 2; } /* output all the subsets of {1, 2, 3} */ int main() { int n = 3; int a[4]; backtrack(a, 0, n); return 0; } 22

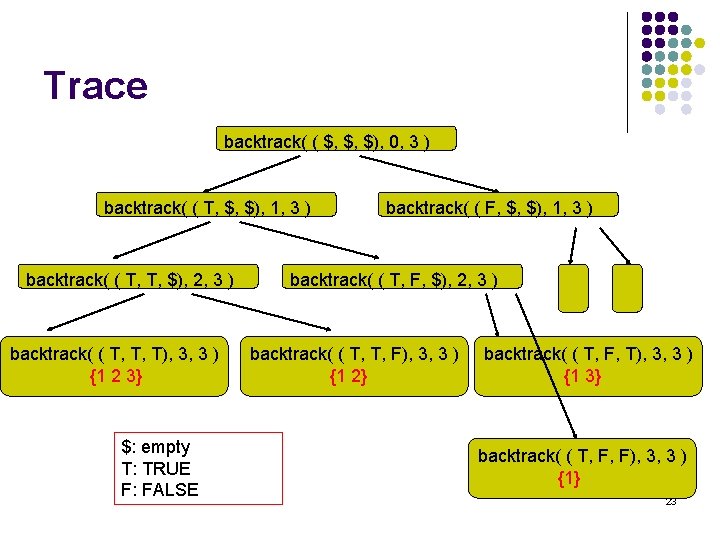
Trace backtrack( ( $, $, $), 0, 3 ) backtrack( ( T, $, $), 1, 3 ) backtrack( ( T, T, $), 2, 3 ) backtrack( ( T, T, T), 3, 3 ) {1 2 3} $: empty T: TRUE F: FALSE backtrack( ( F, $, $), 1, 3 ) backtrack( ( T, F, $), 2, 3 ) backtrack( ( T, T, F), 3, 3 ) {1 2} backtrack( ( T, F, T), 3, 3 ) {1 3} backtrack( ( T, F, F), 3, 3 ) {1} 23

Stone Pile Time Limit: 2. 0 second Memory Limit: 16 MB You have a number of stones with known weights W 1…Wn. Write a program that will rearrange the stones into two piles such that weight difference between the piles is minimal. Input contains the number of stones N (1 ≤ N ≤ 20) and weights of the stones W 1…Wn (1 ≤ Wi ≤ 100000) delimited by white spaces. Your program should output a number representing the minimal possible weight difference between stone piles. Sample input 5 5 8 13 27 14 output 3 24

Example 2: Constructing All Permutations l Permutation of {1, 2, 3} include l l l 123 132 213 231 312 321 Difference from the previous example: When constructing the candidates for the next move, we must ensure that the ith element is distinct from all the elements before it. 25

Constructing All Permutations is_a_solution(int a[], int k, int n) { return (k == n); } process_solution(int a[], int k, int n) { int i; for(i = 1; i <= k; i++) printf(“ %d”, a[i]); printf(“n”); } 26

Constructing All Permutations construct_candidates(int a[], int k, int input, int c[], int *n) { int i; int in_perm[NMAX]; for( i = 1; i < NMAX; i++) in_perm[i] = FALSE; for( i = 1; i < k; i++) in_perm[ a[i] ] = TRUE; *n = 0; for (i = 1; i <= input; i++) if (in_perm[i] == FALSE) { /* candidates must be */ c[*n] = i; /* different from existing */ *n = *n + 1; /* elements */ } } int main() { int n = 3; int a[4]; backtrack(a, 0, n); return 0; } 27

Example 3: Eight-Queens Problem l l The eight queens puzzle is the problem of putting eight chess queens on an 8× 8 chessboard such that none of them is able to capture any other using the standard chess queen's moves. A solution requires that no two queens share the same row, column, or diagonal. How many solutions? http: //en. wikipedia. org/wiki/Eight_queens_puzzle 28

Eight-Queens Problem l l l What is the search space? If a queen can be placed at any square, the search space will be 648. Too large! There are several constrains, which help to reduce the size of search space significantly. l l pruning Consider the queen on the first column, it has 8 choices. Once it has been fixed, consider the queen on the second column, which has 7 choices. It’s easy to see that we have a total of 8! = 40320 cases only. l We haven’t used the diagonal constrain yet. 29

Eight-Queens Problem is_a_solution(int a[], int k, int n) { return (k == n); } process_solution(int a[], int k, int n) { solution_count++; // global count variable } int solution_count; int main() { int n = 8; int a[9]; solution_count = 0; backtrack(a, 0, n); printf(“%dn”, solution_count); return 0; } 30

Eight-Queens Problem construct_candidates(int a[], int k, int input, int c[], int *n) { int i, j; int legal_move; *n = 0; for (i = 1; i <= input; i++) { legal_move = TRUE: for (j = 1; j < k; j++) { if ( abs(k-j) == abs(i-a[j]) ) legal_move == FALSE; /* diagonal threat */ if ( i == a[j] ) legal_move == FALSE; /* column threat */ } if (legal_move == TRUE) { c[*n] = i; *n = *n +1; } } 31 }