Programming for Engineers in Python Recitation 12 Plan

Programming for Engineers in Python Recitation 12

Plan �Dynamic Programming �Coin Change problem �Longest Common Subsequence �Application to Bioinformatics 2

Teaching Survey �Please answer the teaching survey: https: //www. ims. tau. ac. il/Tal/ �This will help us to improve the course �Deadline: 4. 2. 12 3

Coin Change Problem �What is the smallest number of coins I can use to make exact change? �Greedy solution: pick the largest coin first, until you reach the change needed �In the US currency this works well: �Give change for 30 cents if you’ve got 1, 5, 10, and 25 cent coins: � 25 + 5 → 2 coins 4 http: //jeremykun. files. wordpress. com/2012/01/coins. jpg

The Sin of Greediness �What if you don’t have 5 cent coins? �You got 1, 10, and 25 �Greedy solution: 25+1+1+1 → 6 coins �But a better solution is: 10+10+10 → 3 coins! �So the greedy approach isn’t optimal The Seven Deadly Sins and the Four Last Things by Hieronymus Bosch http: //en. wikipedia. org/wiki/File: Boschsevendeadlysins. jpg 5

Recursive Solution �Reminder – find the minimal # of coins needed to give exact change with coins of specified values �Assume that we can use 1 cent coins so there is always some solution �Denote our coin list by c 1, c 2, …, ck (c 1=1) �k is the # of coins values we can use �Denote the change required by n �In the previous example: �n=30, k=3, c 1=1, c 2=10, c 3=25 6

Recursive Solution �Recursion Base: �If n=0 then we need 0 coins �If k=1, c 1=1, so we need n coins �Recursion Step: �If n<ck we can’t use ck → We solve for n and c 1, …, ck-1 �Otherwise, we can either use ck or not use ck �If we use ck → we solve for n-ck and c 1, …, ck �If we don’t use ck → we solve for n and c 1, …, ck-1 7

Recursion Solution def coins_change_rec( cents_needed, coin_values): if cents_needed <= 0: # base 1 return 0 elif len(coin_values) == 1: # base 2 return cents_needed # assume that coin_values[0]==1 elif coin_values[-1] > cents_needed: # step 1 return coins_change_rec( cents_needed, coin_values[: -1]) else: # step 2 s 1 = coins_change_rec( cents_needed, coin_values[: -1] ) s 2 = coins_change_rec( cents_needed-coin_values[-1], coin_values ) return min(s 1, s 2+1) 8 coins_rec. py

Repeated calls � We count how many times we call the recursive function for each set of arguments: calls = {} def coins_change_rec(cents_needed, coin_values): global calls[(cents_needed, coin_values)] = calls. get( (cents_needed, coin_values) , 0) + 1 … >>> print 'result', coins_change_rec(30, (1, 5, 10, 25)) result 2 >>> print 'max calls', max(calls. values()) max calls 4 9

Dynamic Programing - Memoization �We want to store the values of calculation so we don’t repeat them �We create a table called mem �# of columns: # of cents needed + 1 �# of rows: # of coin values + 1 �The table is initialized with some illegal value – for example -1: mem = [ [-1 for y in range(cents_needed+1)] for x in range(len(coin_values)) ] 10

Dynamic Programing - Memoization �For each call of the recursive function, we check if mem already has the answer: if mem[len(coin_values)][cents_needed] == -1: �In case that it doesn’t (the above is True) we calculate it as before, and we store the result, for example: if cents_needed <= 0: mem[len(coin_values)][cents_needed] = 0 �Eventually we return the value return mem[len(coin_values)][cents_needed] 11 coins_mem. py

Dynamic Programing - Iteration �Another approach is to first build the entire matrix �This matrix holds the minimal number of coins we need to get change for j cents using the first i coins (c 1, c 2, …, ci) �The solution will be min_coins[k, n] – the last element in the matrix �This will save us the recursive calls, but will enforce us to calculate all the values apriori �Bottom-up approach vs. the top-down approach of memoization 12

Dynamic Programming approach �The point of this approach is that we have a recursive formula to break apart a problem to sub problems �Then we can use different approaches to minimize the number of calculations by storing the sub solutions in memory 13

Bottom up - example matrix � 14

Bottom up - example matrix �For particular choice of i, j (but not i=0 or j=0) �To determine min_coins[i, j] – the minimum # of 15 coins to get exact change of j using the first i coins �We can use the coin ci and add +1 to min_coins[i, jci] (only valid if j>ci) �We can decide not to use ci , therefore to use only c 0 , . . , ci-1, and therefore min_coins[i-1, j]. �So which way do we choose? �The one with the least coins! min_coins[i, j] = min(min_coins[i, j-ci] +1, min_coins[i-1, j])

Example matrix – recursion step � 16 coins_matrix. py The code for the matrix solution and the idea is from http: //jeremykun. wordpress. com/2012/01/12/a-spoonful-of-python/

Longest Common Subsequence �Given two sequences (strings/lists) we want to find the longest common subsequence �Definition – subsequence: B is a subsequence of A if B can be derived from A by removing elements from A �Examples �[2, 4, 6] is a subsequence of [1, 2, 3, 4, 5, 6] �[6, 4, 2] is NOT a subsequence of [1, 2, 3, 4, 5, 6] �‘is’ is a subsequence of ‘distance’ �‘nice’ is NOT a subsequence of ‘distance’ 17

Longest Common Subsequence �Given two subsequences (strings or lists) we want to find the longest common subsequence: �Example for a LCS: �Sequence 1: HUMAN �Sequence 2: CHIMPANZEE �Applications include: �Bio. Informatics (next up) �Version Control 18 http: //wordaligned. org/articles/longest-common-subsequence

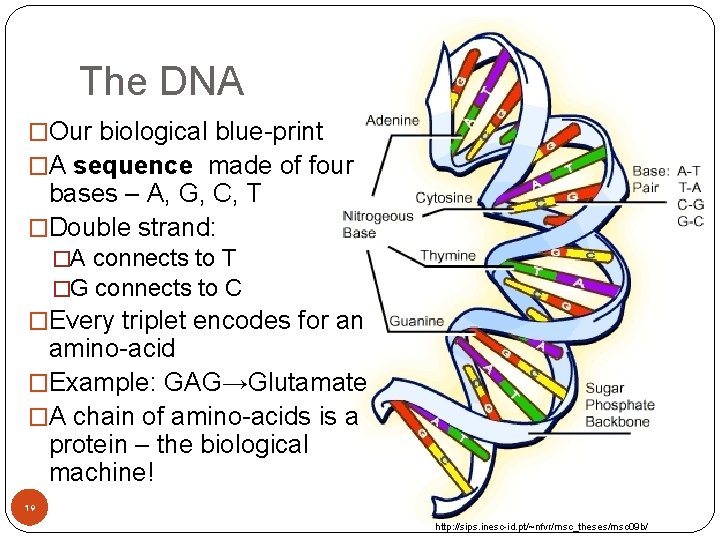
The DNA �Our biological blue-print �A sequence made of four bases – A, G, C, T �Double strand: �A connects to T �G connects to C �Every triplet encodes for an amino-acid �Example: GAG→Glutamate �A chain of amino-acids is a protein – the biological machine! 19 http: //sips. inesc-id. pt/~nfvr/msc_theses/msc 09 b/

Longest common subsequence �The DNA changes: �Mutation: A→G, C→T, etc. �Insertion: AGC → ATGC �Deletion: AGC → A‒C http: //palscience. com/wp-content/uploads/2010/09/DNA_with_mutation. jpg �Given two non-identical sequences, we want to 20 find the parts that are common �So we can say how different they are �Which DNA is more similar to ours? The cat’s or the dog’s?

Recursion �An LCS of two sequences can be built from the 21 LCSes of prefixes of these sequences �Denote the sequences seq 1 and seq 2 �Base – check if either sequence is empty: If len(seq 1) == 0 or len(seq 2) == 0: return [ ] �Step – build solution from shorter sequences: If seq 1[-1] == seq 2[-1]: return lcs (seq 1[: -1], seq 2[: -1]) + [ seq 1[-1] ] else: return max(lcs (seq 1[: -1], seq 2), lcs(seq 1, seq 2[: -1]), key = len) lcs_rec. py

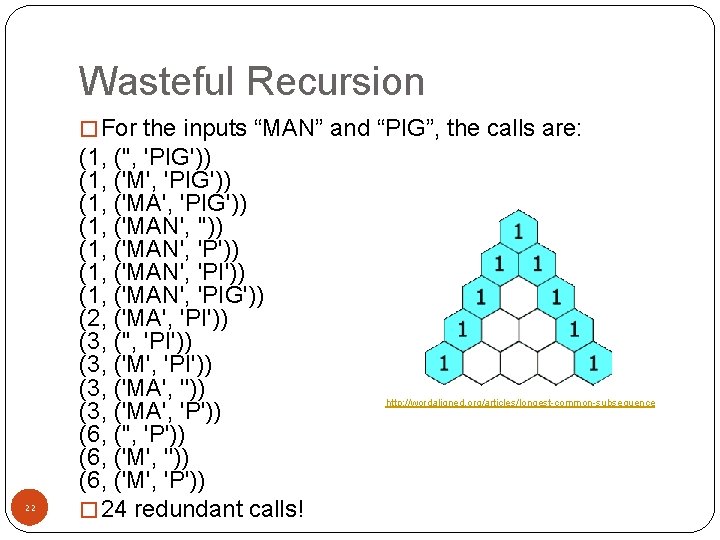
Wasteful Recursion � For the inputs “MAN” and “PIG”, the calls are: 22 (1, ('', 'PIG')) (1, ('MA', 'PIG')) (1, ('MAN', 'P')) (1, ('MAN', 'PIG')) (2, ('MA', 'PI')) (3, ('M', 'PI')) (3, ('MA', 'P')) (6, ('', 'P')) (6, ('M', 'P')) � 24 redundant calls! http: //wordaligned. org/articles/longest-common-subsequence

Wasteful Recursion �When comparing longer sequences with a small number of letters the problem is worse �For example, DNA sequences are composed of A, G, T and C, and are long �For lcs('ACCGGTCGAGTGCGCGGAAGCCGAA', 'GTCGTTCGGAATGCCGTTGCTCTGTAAA') we get an absurd: (('', 'GT'), 13, 182, 769) (('A', 'G'), 24, 853, 152) (('A', ''), 24, 853, 152) 23 http: //blog. oncofertility. northwestern. edu/wpcontent/uploads/2010/07/DNA-sequence. jpg

DP Saves the Day �We saw the overlapping sub problems emerge – comparing the same sequences over and over again �We saw how we can find the solution from solution of sub problems – a property we called optimal substructure �Therefore we will apply a dynamic programming approach �Start with top-down approach - memoization 24

Memoization � We save results of function calls to refrain from calculating them again def lcs_mem( seq 1, seq 2, mem=None ): if not mem: mem = { } key = (len(seq 1), len(seq 2)) # tuples are immutable if key not in mem: # result not saved yet if len(seq 1) == 0 or len(seq 2) == 0: mem[key] = [ ] else: if seq 1[-1] == seq 2[-1]: mem[key] = lcs_mem(seq 1[: -1], seq 2[: -1], mem) + [ seq 1[-1] ] else: mem[key] = max(lcs_mem(seq 1[: -1], seq 2 , mem), lcs_mem (seq 1, seq 2[: -1], mem), key=len ) return mem[key] 25

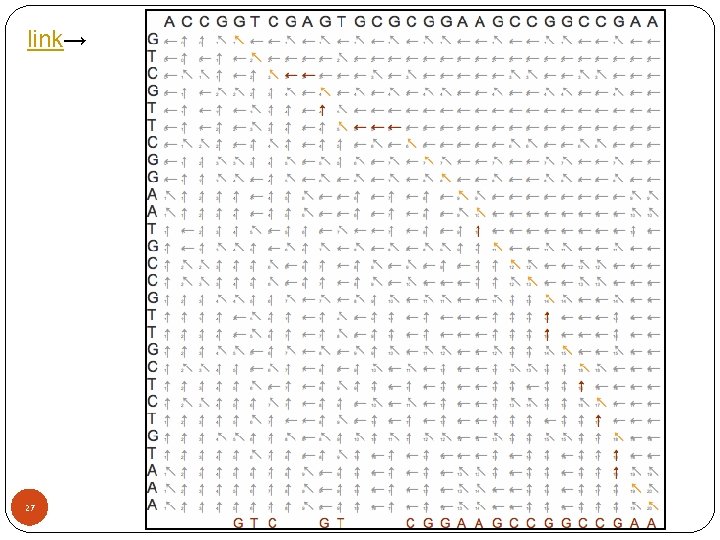
“maximum recursion depth exceeded” �We want to use our memoized LCS algorithm on two 26 long DNA sequences: >>> from random import choice >>> def base(): … return choice('AGCT') >>> seq 1 = str([base() for x in range(10000)]) >>> seq 2 = str([base() for x in range(10000)]) >>>print lcs(seq 1, seq 2) Runtime. Error: maximum recursion depth exceeded in cmp �We need a different algorithm…

link→ 27

DNA Sequence Alignment �Needleman-Wunsch DP Algorithm: �Python package: http: //pypi. python. org/pypi/nwalign �On-line example: http: //alggen. lsi. upc. es/docencia/ember/frameember. html �Code: needleman_wunsch_algorithm. py �Lecture videos from TAU: �http: //video. tau. ac. il/index. php? option=com_videos& view=video&id=4168&Itemid=53 28