Programming for Engineers in Python Lecture 8 Recursion

Programming for Engineers in Python Lecture 8: Recursion Autumn 2011 -12 1

Lecture 7: Highlights 2

Lecture 6 (OOP): Highlights • Representation design options and implications (Rectangle) • Inheritance and Polymorphism • Rational - customize classes so that they are natural to use • Attributes, methods, constructor • Method overriding (e. g. , __str__) • Operators overloading (e. g. , __add__) 3

Variables in Functions • Defined only in the function’s scope • Are not available for other functions/shell (even function’s parameters) • Upon completion of execution: • Variables are not defined anymore • Variables values are not kept for future invocations of the function 4

The Call Stack call stack main result base power exponent =5 3 2 = 17 15 20 i res 5

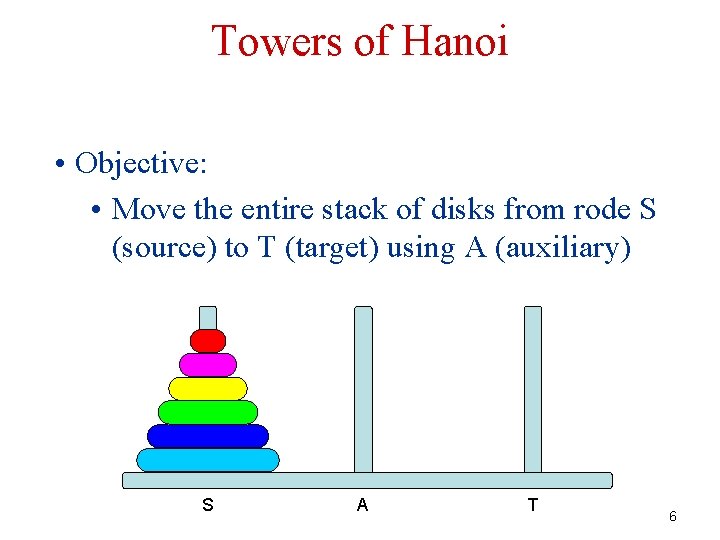
Towers of Hanoi • Objective: • Move the entire stack of disks from rode S (source) to T (target) using A (auxiliary) S A T 6

The Rules • Only one disk may be moved at a time • Each move consists of taking the upper disk from one of the rods and sliding it onto another rod • No disk may be placed on top of a smaller disk S A T 7

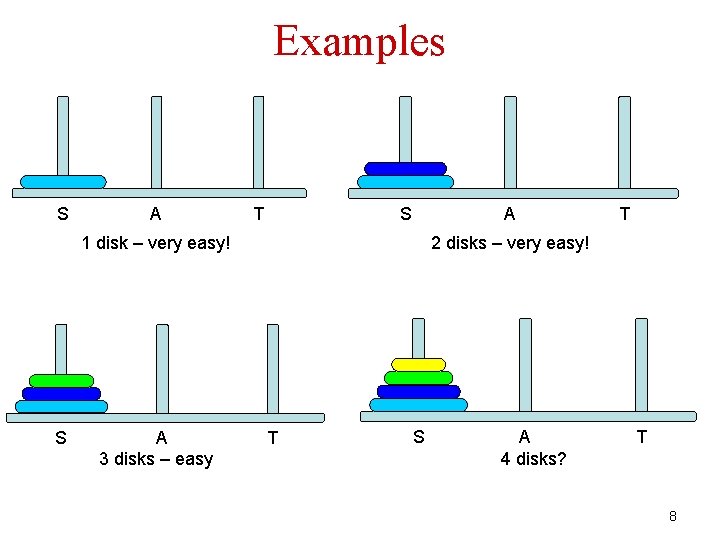
Examples S A T S A 1 disk – very easy! S A 3 disks – easy T 2 disks – very easy! T S A 4 disks? T 8

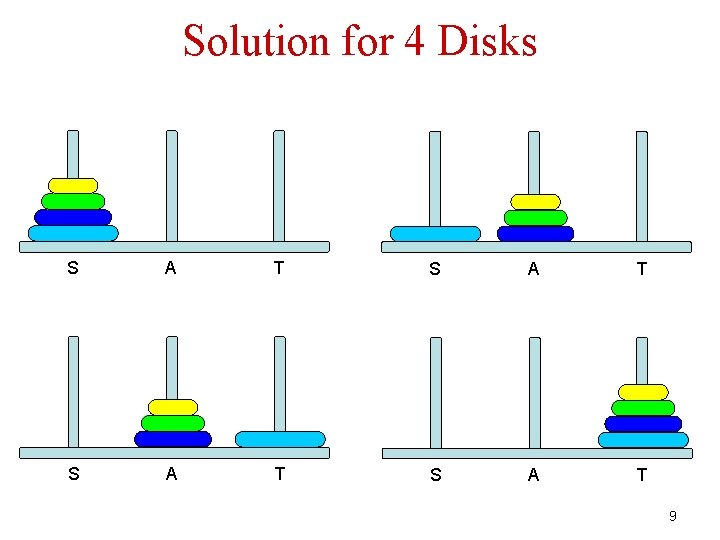
Solution for 4 Disks S A T 9

For n Disks? S A T 10

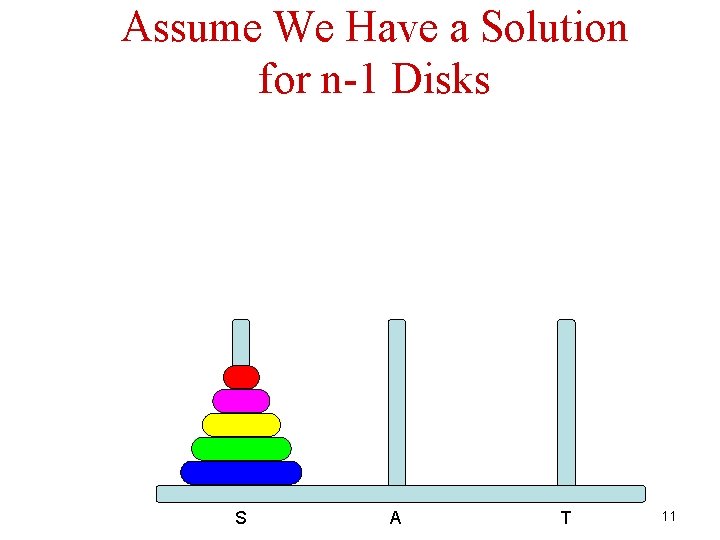
Assume We Have a Solution for n-1 Disks S A T 11

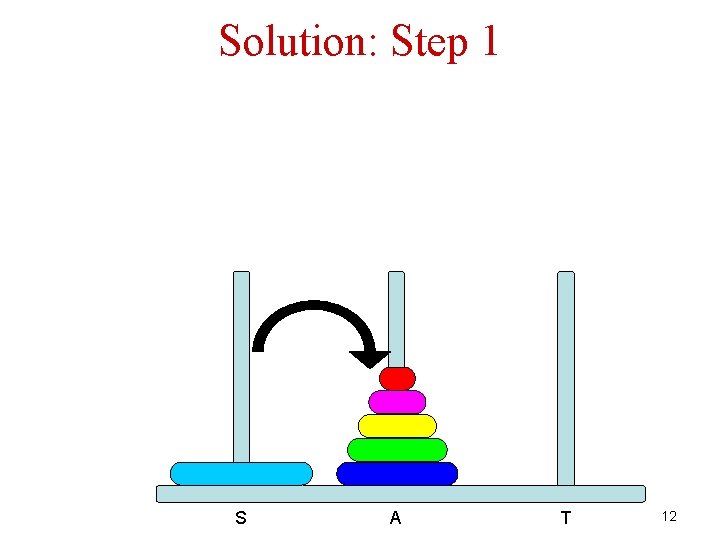
Solution: Step 1 S A T 12

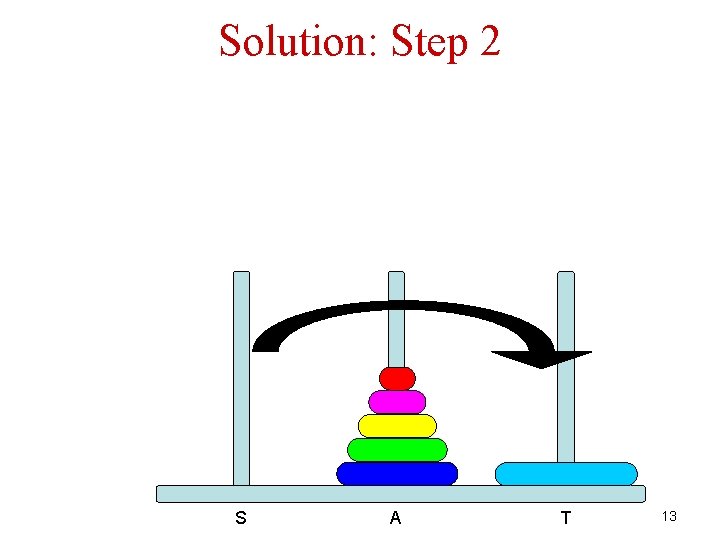
Solution: Step 2 S A T 13

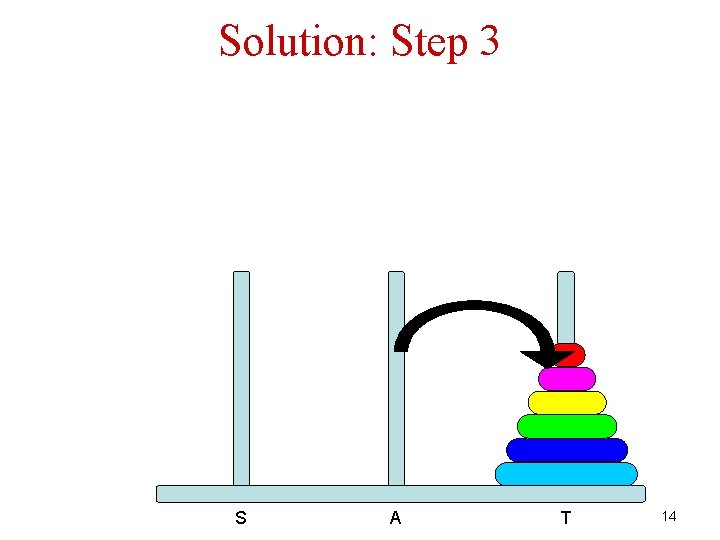
Solution: Step 3 S A T 14

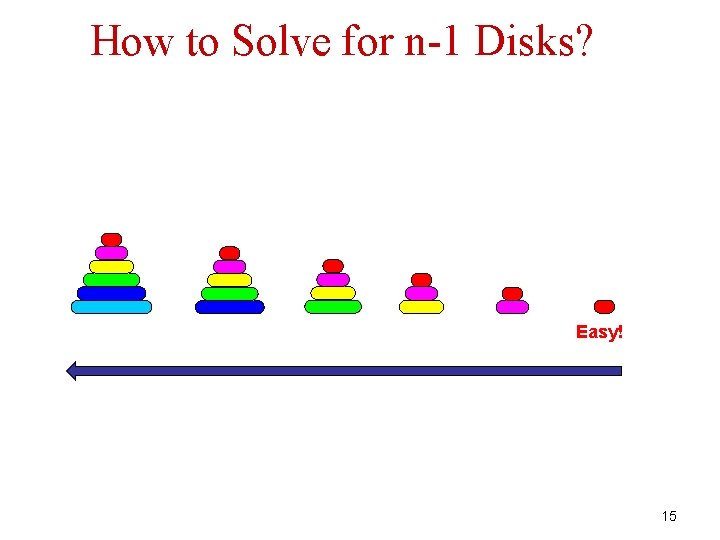
How to Solve for n-1 Disks? Easy! 15

Algorithm for n Disks S 1. 2. 3. 4. A T If there is only a single disk – easy! Move n-1 disks from S to A (T is the auxiliary rode) Move disk from S to T Move n-1 disks from A to T (S is the auxiliary rode) Let us write it in Python… 16

A Python Program for Towers of Hanoi 17

Remember the Calling Stack? main hanoi(3, 'S', 'T', 'A') hanoi(2, 'S', ‘A', ‘T') hanoi(1, ‘S', ‘T', ‘A') And so on… 18

Recursion • We use Recursion to solve the Towers of Hanoi problem • Recursion: a function whose implementation references itself • Recursion enables to solve a “large” problem using solutions to “small” problems that assemble it • In every recursive call the problem is reduced. When the problem is small enough -solve directly (base case, )מקרה קצה • Divide and conquer 19

Iterative Versus Recursive n! = 1*2*3*…. *n an = a*a*…. . *a Step by step (iteratively): 4! = 1*2*3*4 = 6*4 = 24 24 = 2*2*2*2 = 4*2*2 = 8*2 = 16 n iterations n! = n*(n-1)! 0! = 1 Recursively: 4! = 4*3! = 4*(3*2!) = 4*(3*(2*1!)) = 4*(3*(2*(1*0!))) = 4*(3*(2*(1*1))) = 4*(3*(2*1)) = 4*(3*2) = 4*6 = 24 20

Recursive Definition Factorial Recursive call n! = n*(n-1)! 0! = 1 Base condition Smaller instance מקרה קצה 21

Pros and Cons • Pros: short and natural for many problems • Cons: Computational inefficient, sometimes hard to understand or inconvenient 22

Recursion Example in Python Halting condition (and infinite loops) Advance towards base case 23

Recursive factorial – step by step factorial(4) n 4 Returns… 24

Recursive factorial – step by step factorial(4) n 4 Returns… 4*… 25

Recursive factorial – step by step factorial(4) factorial(3) n 4 n 3 Returns… 26

Recursive factorial – step by step factorial(4) factorial(3) n 4 n 3 Returns… 27

Recursive factorial – step by step factorial(4) factorial(3) n 4 n 3 Returns… 3*… 28

Recursive factorial – step by step factorial(4) factorial(3) n 4 factorial(2) n 3 n Returns… 29

Recursive factorial – step by step factorial(4) factorial(3) n 4 factorial(2) n 3 n Returns… 2 Returns… 30

Recursive factorial – step by step factorial(4) factorial(3) n 4 factorial(2) n 3 n Returns… 2*… 31

Recursive factorial – step by step factorial(4) factorial(3) n 4 factorial(2) n 3 factorial(1) n Returns… 2 n Returns… 1 Returns… 32

Recursive factorial – step by step factorial(4) factorial(3) n 4 factorial(2) n 3 factorial(1) n Returns… 2 n Returns… 1 Returns… 33

Recursive factorial – step by step factorial(4) factorial(3) n 4 factorial(2) n 3 factorial(1) n Returns… 2 n Returns… 1*… 34

Recursive factorial – step by step factorial(4) factorial(3) n 4 factorial(2) n 3 factorial(1) n Returns… 2 factorial(0) n Returns… 1 n Returns… 0 Returns… 35

Recursive factorial – step by step factorial(4) factorial(3) n 4 factorial(2) n 3 factorial(1) n Returns… 2 factorial(0) n Returns… 1 n Returns… 0 Returns… 36

Recursive factorial – step by step factorial(4) factorial(3) n 4 factorial(2) n 3 factorial(1) n Returns… 2 factorial(0) n Returns… 1 n Returns… 0 Returns… 37

Recursive factorial – step by step factorial(4) factorial(3) n 4 factorial(2) n 3 factorial(1) n Returns… 2 factorial(0) n Returns… 1 n Returns… 0 Returns… 1 38

Recursive factorial – step by step factorial(4) factorial(3) n 4 factorial(2) n 3 factorial(1) n Returns… 2 n Returns… 1*1 39

Recursive factorial – step by step factorial(4) factorial(3) n 4 factorial(2) n 3 n Returns… 2*1 40

Recursive factorial – step by step factorial(4) factorial(3) n 4 n 3 Returns… 3*2 41

Recursive factorial – step by step factorial(4) n 4 Returns… 4*6 42

General Form of Recursive Algorithms test + base case recursive case • Base case: small (non-decomposable) problem • Recursive case: larger (decomposable) problem • At least one base case, and at least one recursive case. 43

Short Summary • Design a recursive algorithm by 1. Solving big instances using the solution to smaller instances 2. Solving directly the base cases • Recursive algorithms have 1. Stopping criteria 2. Recursive case(s) 3. Construction of a solution using solution to smaller instances 44

Point for Attention: Memory • Variables of a called function are kept in memory until the function returns • Many recursive calls might fill the computers memory • Even if we minimize the number of variables, recursion has its price 45

Example: Fibonacci Series • Fibonacci series 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 • Definition: • fib(0) = 0 • fib(1) = 1 • fib(n) = fib(n-1) + fib(n-2) en. wikipedia. org/wiki/Fibonacci_number 46

Recursive Fibonacci Series Every call with n > 1 invokes 2 function calls, and so on… 48

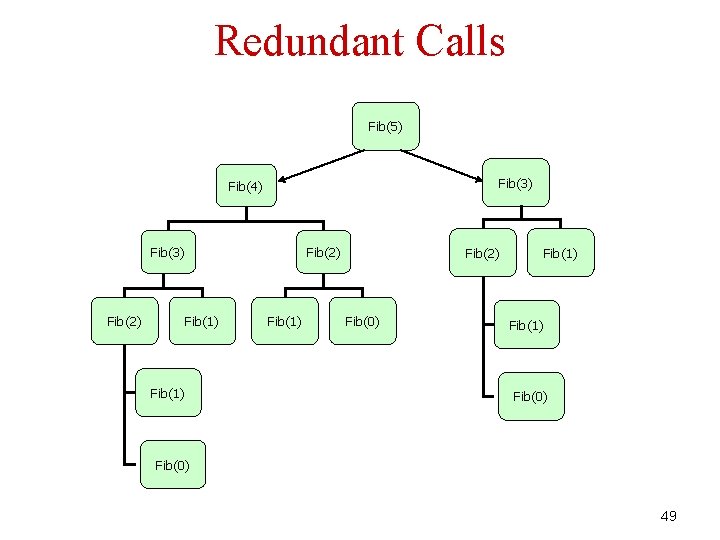
Redundant Calls Fib(5) Fib(3) Fib(4) Fib(3) Fib(2) Fib(1) Fib(2) Fib(0) Fib(1) Fib(0) 49

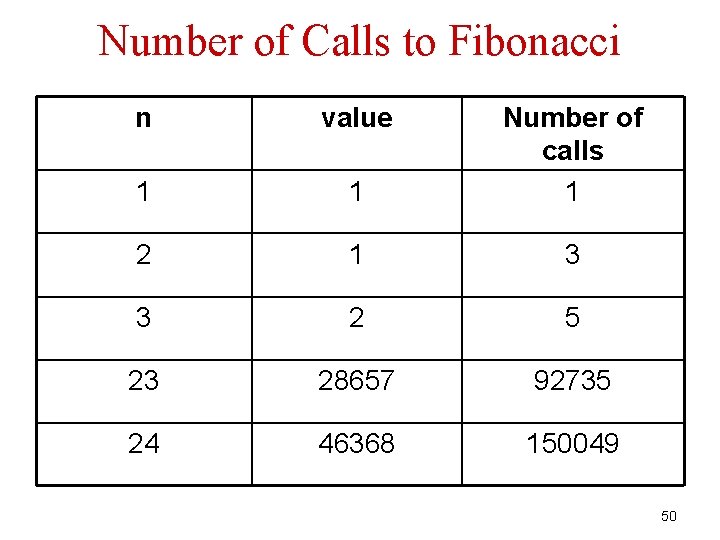
Number of Calls to Fibonacci n value 1 1 Number of calls 1 2 1 3 3 2 5 23 28657 92735 24 46368 150049 50

Demonstration: Iterative Versus Recursive Fibonacci 51

Demonstration: Iterative Versus Recursive Fibonacci Output (shell): 52

Fibonacci: Recursion and Efficiency • If a recursive function calls itself more than once it will be extremely inefficient • Define it iteratively 53

So Do We Really Need Recursion? Yes! (specific examples next week) 54

Odd-Even (if time allows) • Given a function ‘odd(n)’ • Odd n - return True, Even n – return False • Write a function ‘even(n)’ that: • Even n - return True, Odd n – return False • This is easy! 55

Odd-Even 56

Odd-Even 57

Odd-Even 58

Odd-Even 59

Questions?

Off Topics • Documenting your programs • Find the error 61

Documenting Your Programs • An essential part of writing computer code • Understand what was your intension when writing it • For others to be able to coordinate their code with yours • For the grader/lecturer to try and understand your code and grade it accordingly… 62

Documenting Your Programs with Comments • Comments: pieces of code not interpreted or executed by the computer • One line comments start with the hash character (#) 63

Meaningful Variables Names • Variables names • Meaningful names 64

Off Topic: Find the Error

And Now?

And Now?

INDENTATION IS REALLY, REALLY IMPORTANT!