Programming Data Structures and Algorithms Priority Queues Anton

Programming, Data Structures and Algorithms (Priority Queues) Anton Biasizzo Programming, Data Structures and Algorithms (Priority Queues) Slide 1/53

Priority Queue q Jobs that are put on the queue have different priorities. q Very important job should be processed first. q Priority queue ADT is data structure that provides following two operations: § Insert operation (Enqueue operation) § Delete. Min operation, which finds, returns, and removes the minimum element from the queue. q Other operations are possible. Programming, Data Structures and Algorithms (Priority Queues) Slide 2/53

Simplementation q Use simple linked list § Perform insertions in front (O(1)). § Traverse the list to delete the minimum (O(n)). q Use ordered linked list § Expensive insertions (O(n)). § Cheap Delete. Min (O(1)). q Use binary search tree § Both operations require O(log n) time. § Only subset of operation is used. Programming, Data Structures and Algorithms (Priority Queues) Slide 3/53

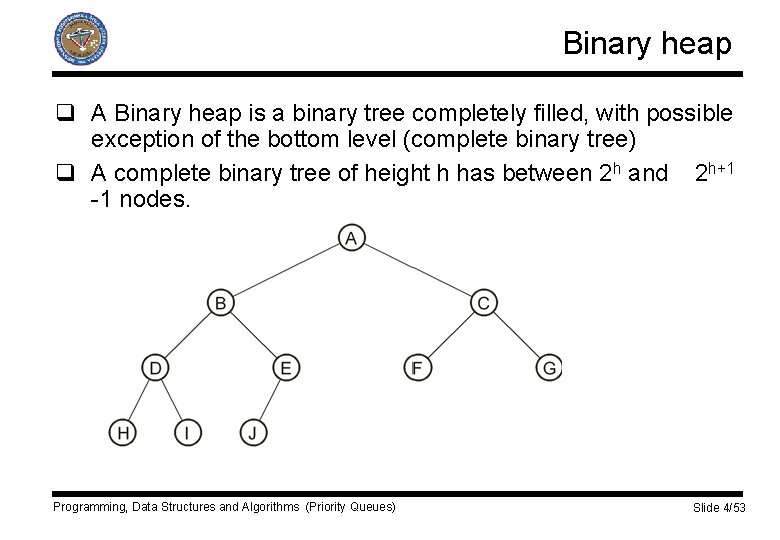
Binary heap q A Binary heap is a binary tree completely filled, with possible exception of the bottom level (complete binary tree) q A complete binary tree of height h has between 2 h and 2 h+1 -1 nodes. Programming, Data Structures and Algorithms (Priority Queues) Slide 4/53

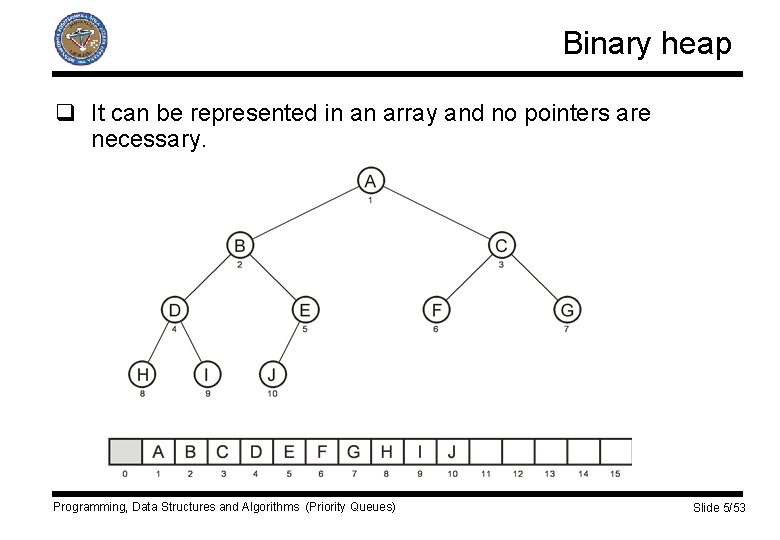
Binary heap q It can be represented in an array and no pointers are necessary. Programming, Data Structures and Algorithms (Priority Queues) Slide 5/53

Binary heap q For an element in array position i: § the left child is in position 2 i, § the right child is in position 2 i + 1 , § the parent is in position [i/2]. q Operations for tree traversing are simple and very fast. q Heap size must be estimated in advance. q Heap order property: § In order to perform operations quickly the smallest element should be at the root. § Any subtree should also be heap: any node should be smaller than its descendants. Programming, Data Structures and Algorithms (Priority Queues) Slide 6/53

Heap type declaration q Type declaration and initialization: struct heap_struct { unsigned int max_heap_size; unsigned int size; element_type *elements; }; typedef struct heap_struct *PRIORITY_QUEUE; PRIORITY_QUEUE create_pq(unsigned int max_elements) { PRIORITY_QUEUE H; H = (PRIORITY_QUEUE) malloc ( sizeof (struct heap_struct) ); H->elements = (element_type *) malloc ( (max_elements+1) * sizeof (element_type) ); H->max_heap_size = max_elements; H->size = 0; H->elements[0] = MIN_DATA; return H; } Programming, Data Structures and Algorithms (Priority Queues) Slide 7/53

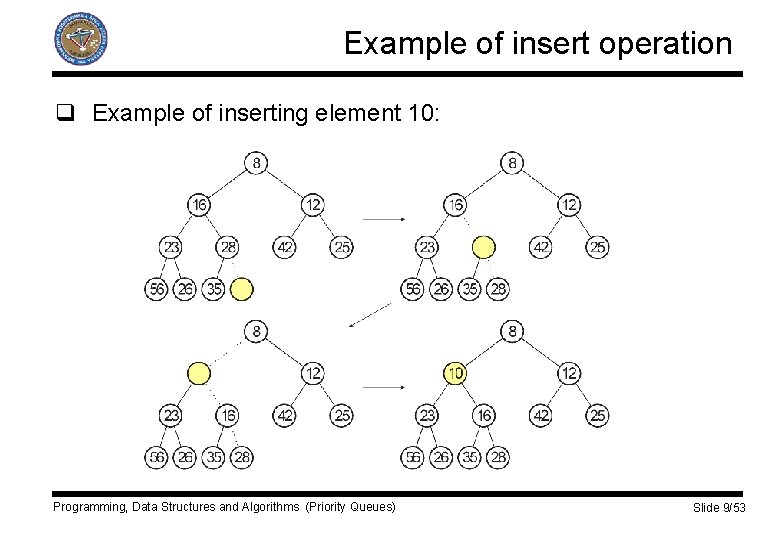
Basic heap operations q We need to insure that heap order is maintained. q Insert element X § Create a hole (empty cell) in next available location. § If X can be placed in the hole without violating heap order then we do so and we are done. § We slide the element that is in hole’s parent to the hole, moving the hole towards the root and repeat from previous step until X is placed in the hole. q This strategy is called percolate up. Programming, Data Structures and Algorithms (Priority Queues) Slide 8/53

Example of insert operation q Example of inserting element 10: Programming, Data Structures and Algorithms (Priority Queues) Slide 9/53

Insert operation q Insert operation void insert( element_type x, PRIORITY_QUEUE H ) { unsigned int i; if ( H->size < H->max_heap_size) { i = ++H->size; H->elements[0] = x; /* optionally create sentinel */ while ( H->elements[i/2] > x ) { H->elements[i] = H->elements[i/2]; i /= 2; } H->elements[i] = x; } else error(“Priority queue is full”); } Programming, Data Structures and Algorithms (Priority Queues) Slide 10/53

Insert operation q Element in position 0 is a sentinel and is used to avoid one test (if) in while loop. q Elements are not switched in each percolation but merely moved down. q Insertion takes O(log n) time in worst case scenario. q On average, the percolation terminates early: it was shown that 2. 607 comparisons are required on average per insertion (O(1)). Programming, Data Structures and Algorithms (Priority Queues) Slide 11/53

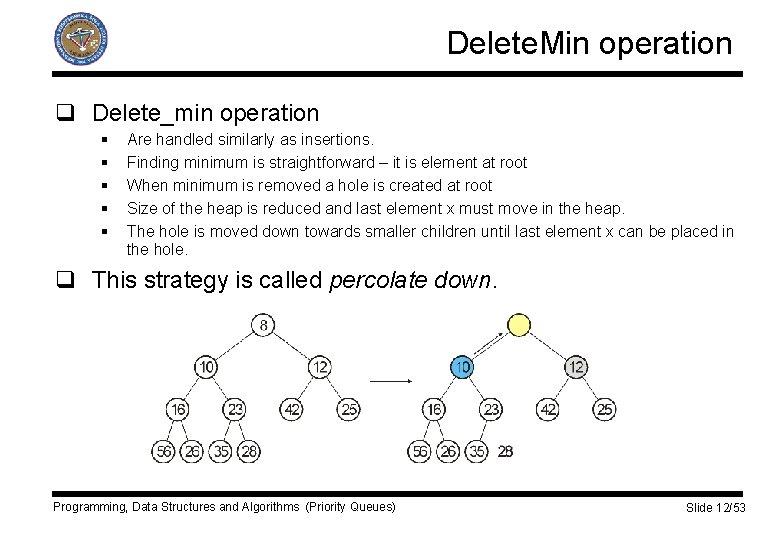
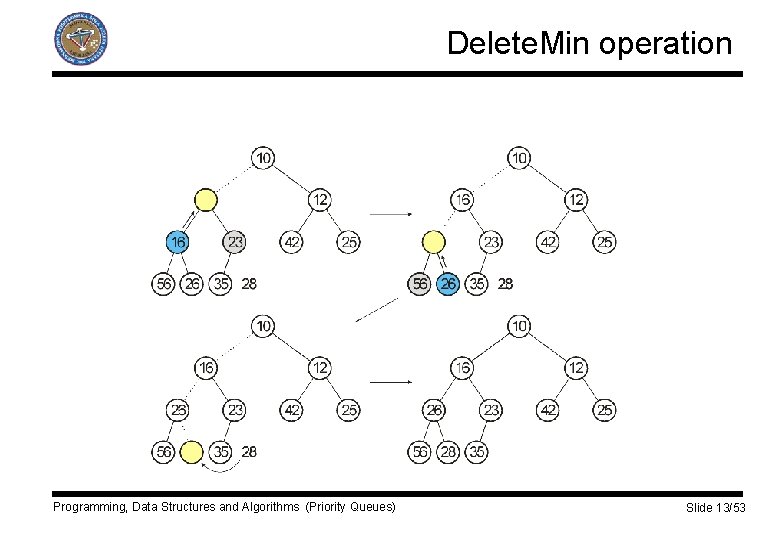
Delete. Min operation q Delete_min operation § § § Are handled similarly as insertions. Finding minimum is straightforward – it is element at root When minimum is removed a hole is created at root Size of the heap is reduced and last element x must move in the heap. The hole is moved down towards smaller children until last element x can be placed in the hole. q This strategy is called percolate down. Programming, Data Structures and Algorithms (Priority Queues) Slide 12/53

Delete. Min operation Programming, Data Structures and Algorithms (Priority Queues) Slide 13/53

Delete. Min operation q Delete. Min operation element_type delete_min( PRIORITY_QUEUE H ) { unsigned int I, child; element_type min_element, last_element; if ( H->size > 0 ) { min_element = H->elements[1]; last_element = H->elements[H->size--]; for ( i=1; i*2 <= H->size; i=child ) { child = i*2; if ( (child != H->size) && ( H->elements[child+1] < H->element[child] ) ) child++; if ( last_element > H->elements[child] ) H->elements[i] = H->elements[child]; else break; } H->elements[i] = last_element; return min_element; } else error(“Priority queue is empty”); } Programming, Data Structures and Algorithms (Priority Queues) Slide 14/53

Delete. Min operation q Like in Insert operation elements are not switched in each percolation but merely pushed up. q Delete. Min takes O(log n) time in worst case scenario. q On average, the hole, which is placed at the root, is percolated almost to the bottom of the heap. q On average Delete. Min takes O(log n) time. Programming, Data Structures and Algorithms (Priority Queues) Slide 15/53

Other heap operations q q Finding minimum element in constant time. Little information on location of maximum element. Maximum element in a leaf node (half of nodes are leaves) If location of element is important (find operation) some other data structure (like hash table) must be implemented in addition to heap. q Some additional operations become cheap if location of elements are known: § § Decrease_key(x, Δ, H) Increase_key(x, Δ, H) Delete(x, H) Build_heap(H) Programming, Data Structures and Algorithms (Priority Queues) Slide 16/53

Other heap operations q Decrease_key(x, Δ, H) lowers the value of the key at position x: § Since this might violate the heap order it must be fixed by percolate up. q Increase_key(x, Δ, H) increases the value of the key at position x: § The heap order is restored by percolate down. q Delete(x, H) removes the node at position x: § First perform Decrease_key(x, ∞, H) operation. § Perform Delete. Min(H) operation. q Build. Heap(H) operation takes n input keys and places them into an empty heap. § It can be done with n successive Inserts, worst case running time is O(n log n), while average is O(n). Programming, Data Structures and Algorithms (Priority Queues) Slide 17/53

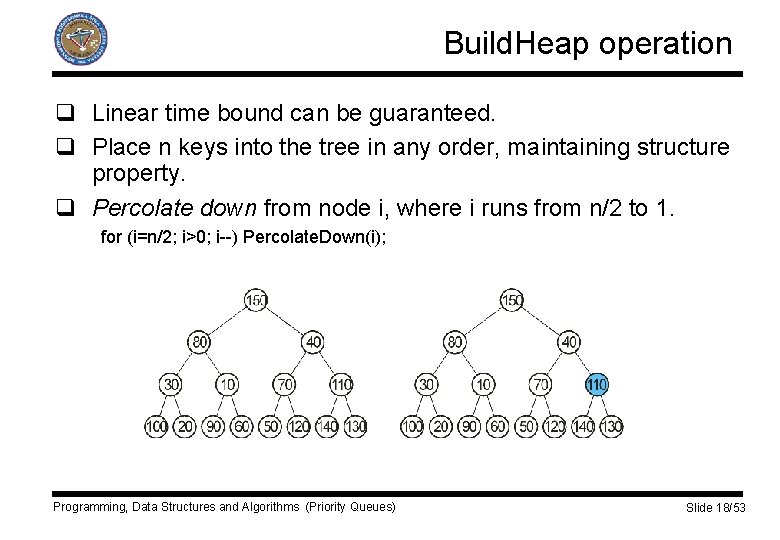
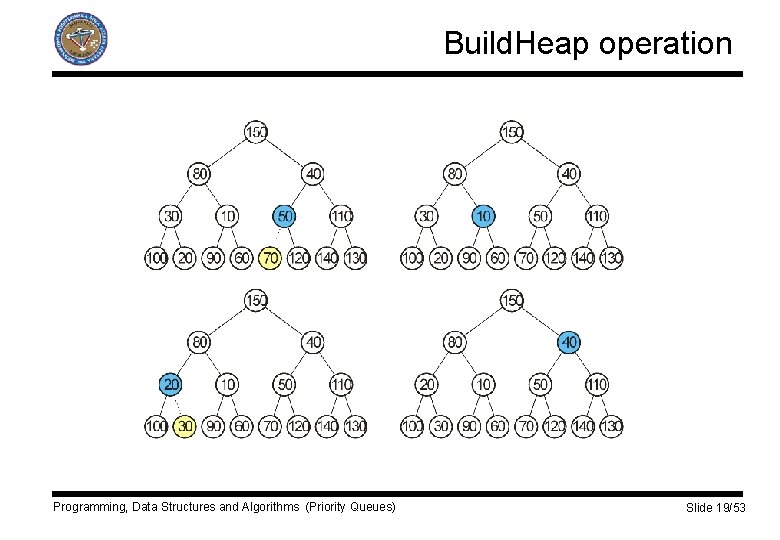
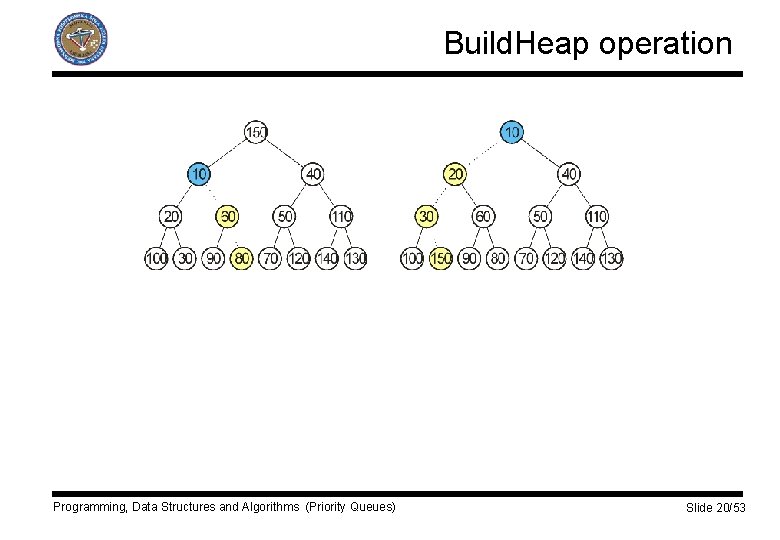
Build. Heap operation q Linear time bound can be guaranteed. q Place n keys into the tree in any order, maintaining structure property. q Percolate down from node i, where i runs from n/2 to 1. for (i=n/2; i>0; i--) Percolate. Down(i); Programming, Data Structures and Algorithms (Priority Queues) Slide 18/53

Build. Heap operation Programming, Data Structures and Algorithms (Priority Queues) Slide 19/53

Build. Heap operation Programming, Data Structures and Algorithms (Priority Queues) Slide 20/53

Applications of Priority queues q Operating systems design q The selection problem: the input is a list of n elements and an integer k, the problem is to find k-th largest element. q Event driven simulation q d-Heaps is a generalization of binary heap: § § Node has d children Improved Insert running time More expensive Delete. Min operation Used where Insert is more often than Delete. Min or heaps are large and don’t fit into memory (analogy with B-trees). Programming, Data Structures and Algorithms (Priority Queues) Slide 21/53

Leftist Heaps q Weakness of heap implementation § Merge operation is difficult q Leftist Heap § Has structural property and ordering property like binary heap. § Leftist heap is not perfectly balanced like binary heap. q Null path length NPL(x): § Is the length of the shortest path from node x to a node without two children. § NPL of a node with zero or one child is 0. q Leftist Heap property § For every node x in the heap the NPL of the left child is at least as large as NPL of the right child. Programming, Data Structures and Algorithms (Priority Queues) Slide 22/53

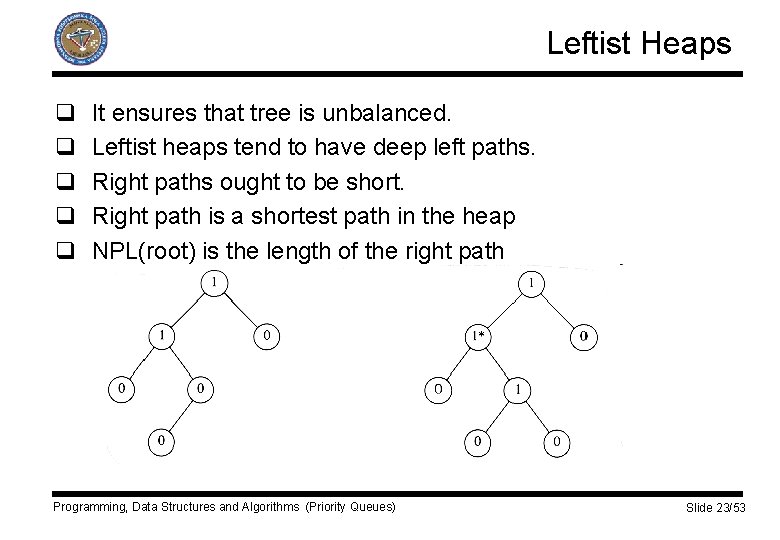
Leftist Heaps q q q It ensures that tree is unbalanced. Leftist heaps tend to have deep left paths. Right paths ought to be short. Right path is a shortest path in the heap NPL(root) is the length of the right path Programming, Data Structures and Algorithms (Priority Queues) Slide 23/53

Leftist Heaps q A leftist tree with r nodes on the right path (NPL=r-1) must have at least 2 r-1 nodes. q Proof by induction: § § § § If r = 1 (single node on right path), there must be at least one tree node. Suppose that theorem is true for 1, 2, . . , r. Consider a leftist tree with r+1 nodes on the right path (NPL=r for root). Root has right subtree with r nodes in right path. Root must have left subtree with at least r nodes in right path. Applying hypothesis each subtree has at least 2 r-1 nodes. Thus the complete leftist tree has 2*(2 r-1) + 1 = 2 r+1 -1 nodes. q A leftist tree of n nodes has a right path containing at most [log(n+1)] nodes. q Heap operation perform on the right path, which is short. Programming, Data Structures and Algorithms (Priority Queues) Slide 24/53

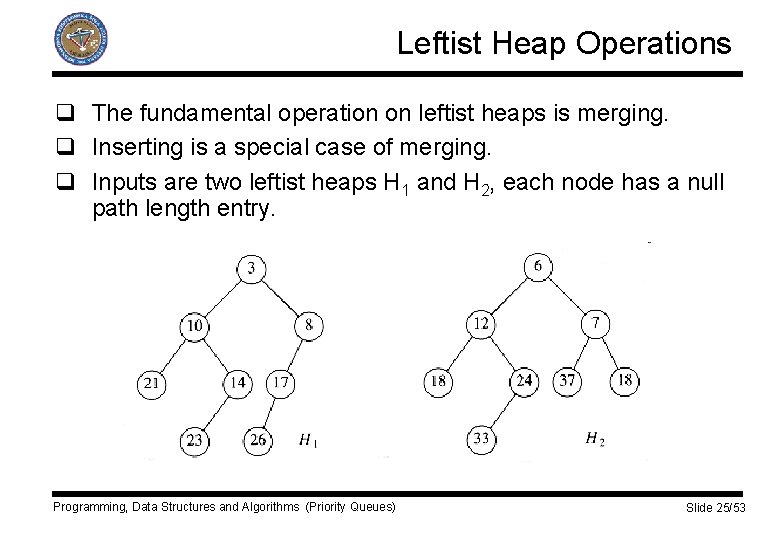
Leftist Heap Operations q The fundamental operation on leftist heaps is merging. q Inserting is a special case of merging. q Inputs are two leftist heaps H 1 and H 2, each node has a null path length entry. Programming, Data Structures and Algorithms (Priority Queues) Slide 25/53

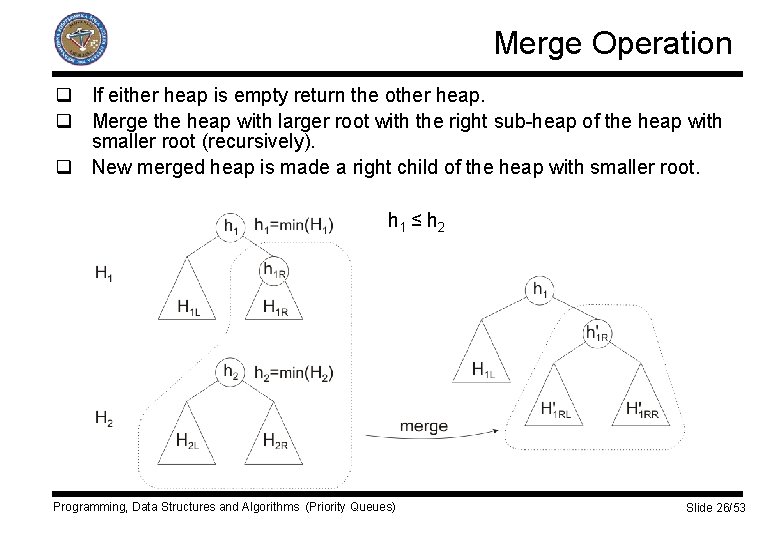
Merge Operation q If either heap is empty return the other heap. q Merge the heap with larger root with the right sub-heap of the heap with smaller root (recursively). q New merged heap is made a right child of the heap with smaller root. h 1 ≤ h 2 Programming, Data Structures and Algorithms (Priority Queues) Slide 26/53

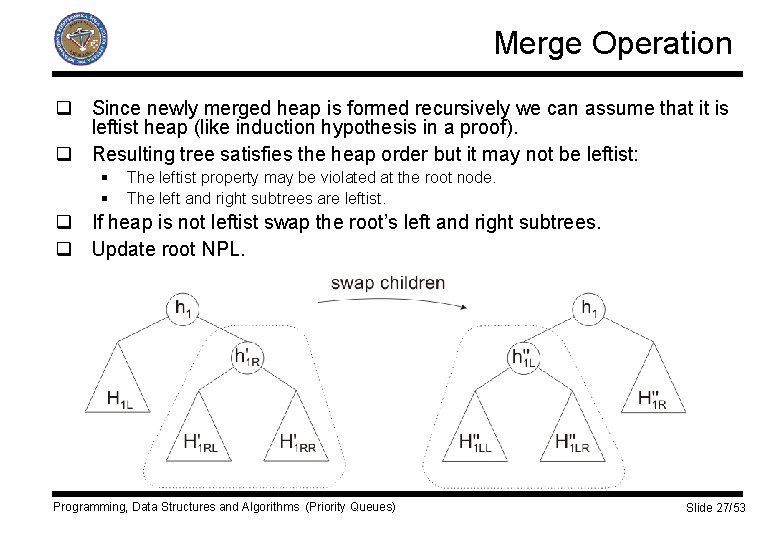
Merge Operation q Since newly merged heap is formed recursively we can assume that it is leftist heap (like induction hypothesis in a proof). q Resulting tree satisfies the heap order but it may not be leftist: § § The leftist property may be violated at the root node. The left and right subtrees are leftist. q If heap is not leftist swap the root’s left and right subtrees. q Update root NPL. Programming, Data Structures and Algorithms (Priority Queues) Slide 27/53

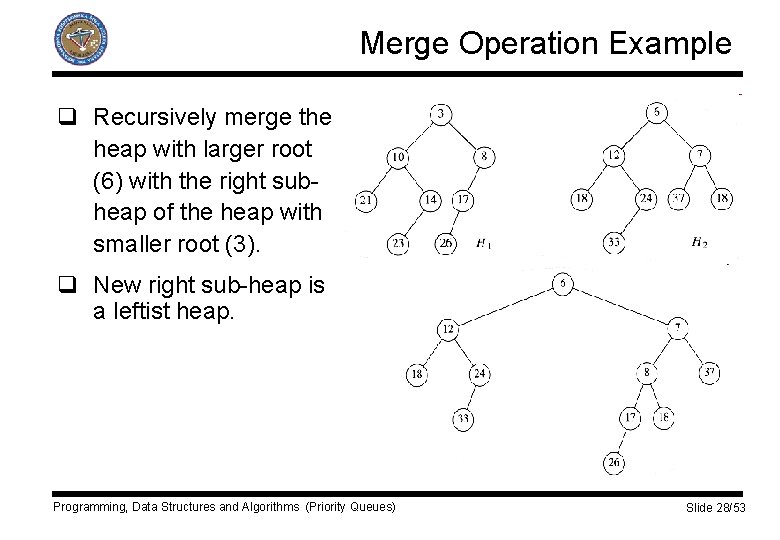
Merge Operation Example q Recursively merge the heap with larger root (6) with the right subheap of the heap with smaller root (3). q New right sub-heap is a leftist heap. Programming, Data Structures and Algorithms (Priority Queues) Slide 28/53

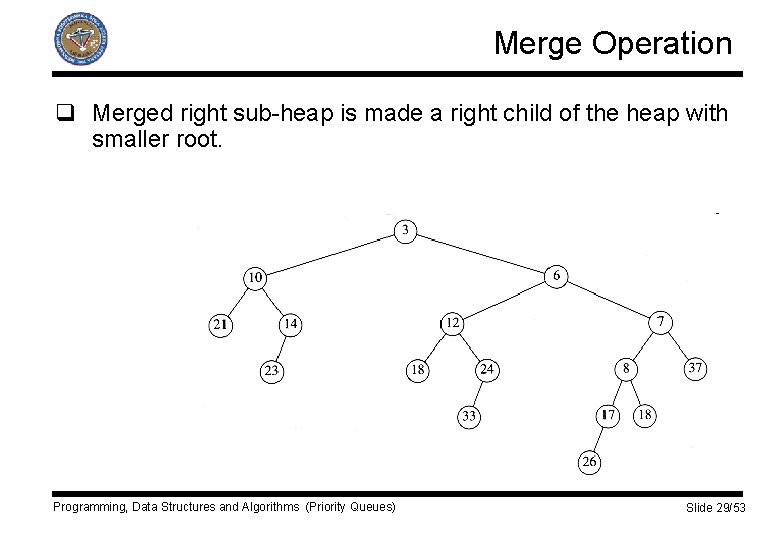
Merge Operation q Merged right sub-heap is made a right child of the heap with smaller root. Programming, Data Structures and Algorithms (Priority Queues) Slide 29/53

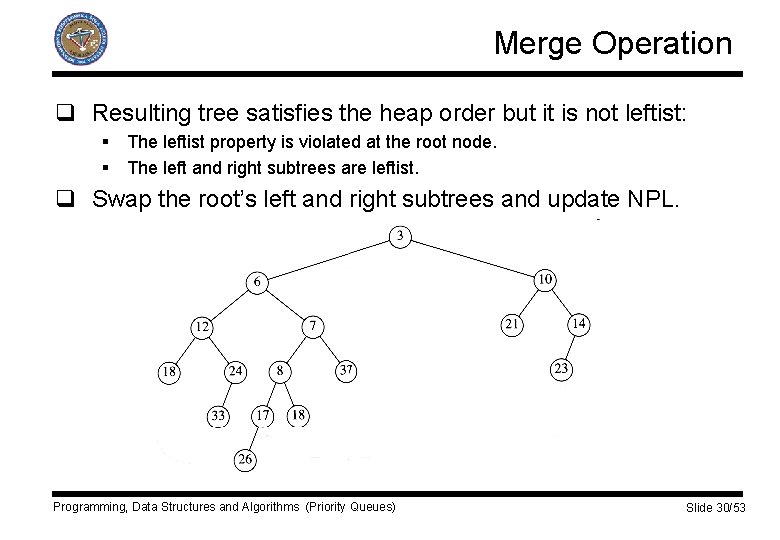
Merge Operation q Resulting tree satisfies the heap order but it is not leftist: § The leftist property is violated at the root node. § The left and right subtrees are leftist. q Swap the root’s left and right subtrees and update NPL. Programming, Data Structures and Algorithms (Priority Queues) Slide 30/53

Merge Operation q Merge operation PRIORITY_QUEUE merge( PRIORITY_QUEUE H 1, PRIORITY_QUEUE H 2) { if ( H 1 == NULL ) return H 2; if ( H 2 == NULL ) return H 1; if ( H 1 ->element < H 2 ->element) return merge 1( H 1, H 2 ); else return merge 1( H 2, H 1); } PRIORITY_QUEUE merge 1( PRIORITY_QUEUE H 1, PRIORITY_QUEUE H 2) { if ( H 1 ->right == NULL ) H 1 ->right = H 2; else { H 1 ->right = merge( H 1 ->right, H 2 ); if (H 1 ->left->npl < H 1 ->right->npl) swap_children( H 1 ); H 1 ->npl = H 1 ->right->npl + 1; return H 1; } Programming, Data Structures and Algorithms (Priority Queues) Slide 31/53

Leftist Operations q If null path length is not updated in merge operation all NPLs would be 0 and the heap would not be leftist but random. q The time to perform merge is proportional to sum of the lengths of the right paths and is O(log n). § At each visited node during recursive calls a constant work is performed. q Insertion is done by making an item to be a one-node heap and performing Merge with the heap. q Delete. Min operation: § Delete root node § Merge left and right subtree § Time to perform Delete. Min is O(log n) Programming, Data Structures and Algorithms (Priority Queues) Slide 32/53

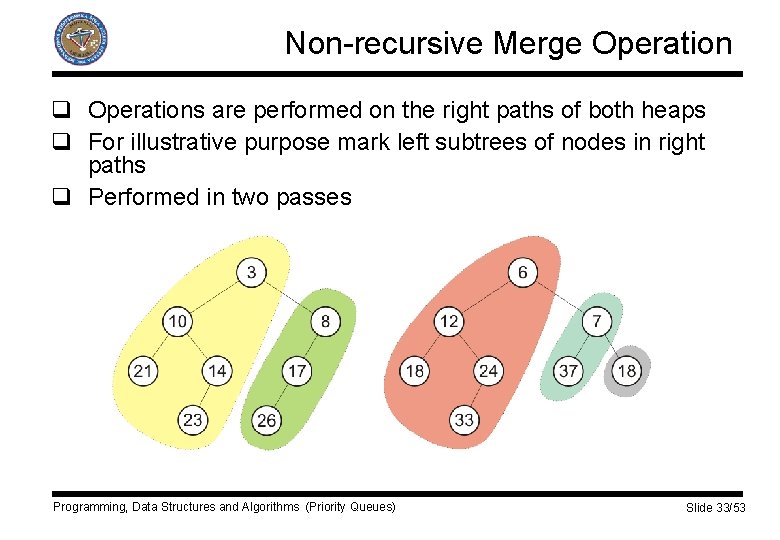
Non-recursive Merge Operation q Operations are performed on the right paths of both heaps q For illustrative purpose mark left subtrees of nodes in right paths q Performed in two passes Programming, Data Structures and Algorithms (Priority Queues) Slide 33/53

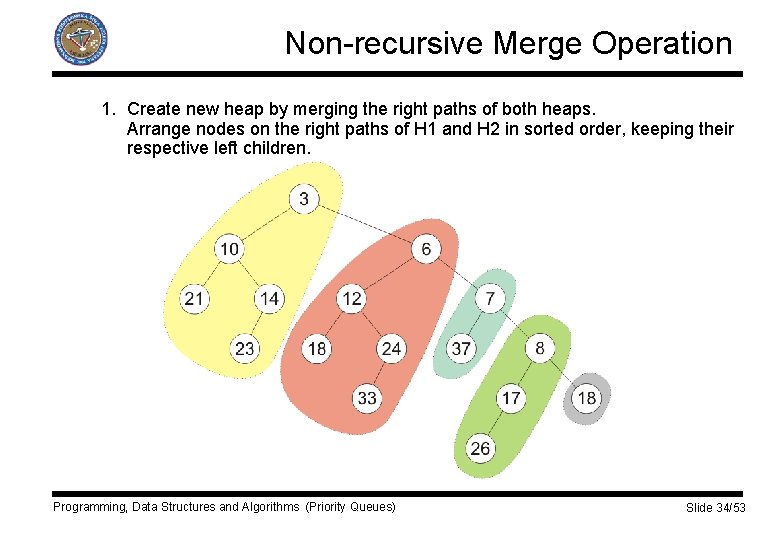
Non-recursive Merge Operation 1. Create new heap by merging the right paths of both heaps. Arrange nodes on the right paths of H 1 and H 2 in sorted order, keeping their respective left children. Programming, Data Structures and Algorithms (Priority Queues) Slide 34/53

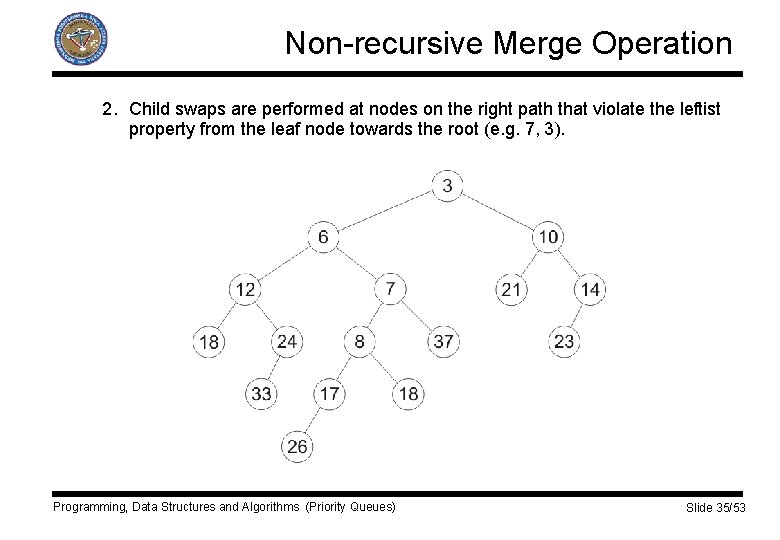
Non-recursive Merge Operation 2. Child swaps are performed at nodes on the right path that violate the leftist property from the leaf node towards the root (e. g. 7, 3). Programming, Data Structures and Algorithms (Priority Queues) Slide 35/53

Leftist Heaps q Unbalanced tree: § Short right path § Tend to have deep left paths q q q Record of null path length in each node is needed. Heap operation performed on the right path, which is short. Merging is fundamental operation. Insert is special case of merge. Delete. Min is implemented by merge. All three operations require O(log n) time. Programming, Data Structures and Algorithms (Priority Queues) Slide 36/53

Skew Heaps q A skew heap is a self-adjusting version of leftist heap. q Skew heaps are § Binary trees with heap order. § There is no structural constraints. § No information is maintained about null path length. q The right path can be arbitrary long at any time – running time for all operations in worst case is O(n). q For m consecutive operations the total worst case running time is O(m log n) – similar to the case of splay trees. Programming, Data Structures and Algorithms (Priority Queues) Slide 37/53

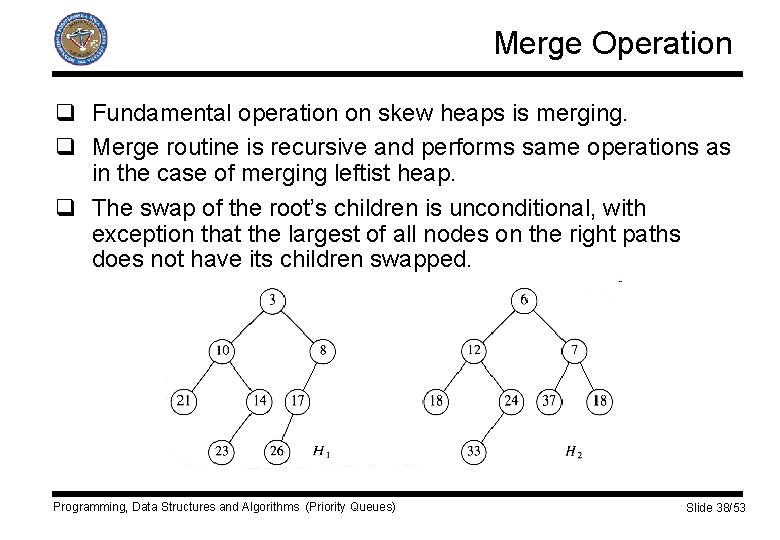
Merge Operation q Fundamental operation on skew heaps is merging. q Merge routine is recursive and performs same operations as in the case of merging leftist heap. q The swap of the root’s children is unconditional, with exception that the largest of all nodes on the right paths does not have its children swapped. Programming, Data Structures and Algorithms (Priority Queues) Slide 38/53

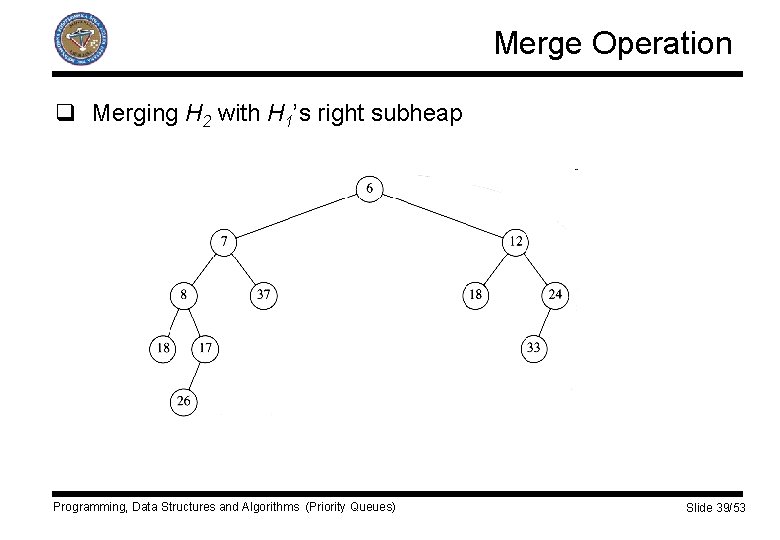
Merge Operation q Merging H 2 with H 1’s right subheap Programming, Data Structures and Algorithms (Priority Queues) Slide 39/53

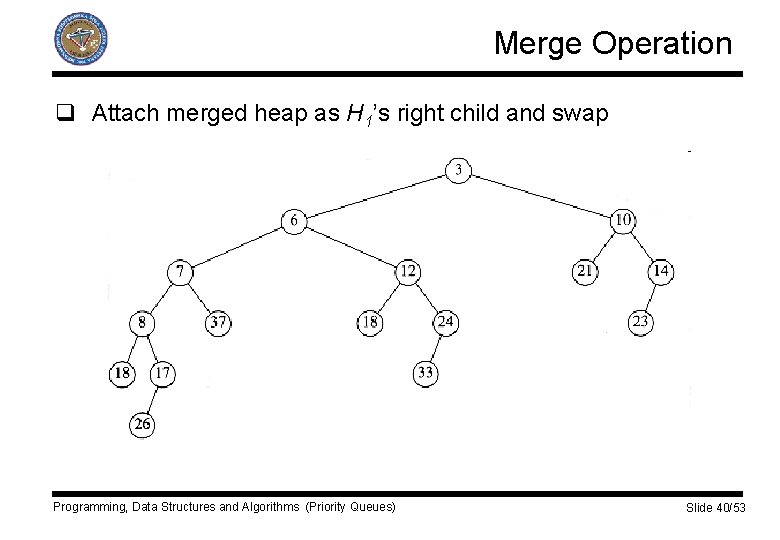
Merge Operation q Attach merged heap as H 1’s right child and swap Programming, Data Structures and Algorithms (Priority Queues) Slide 40/53

Skew Heaps q q q q Skew heap is unbalanced tree Record of null path length in each node is not needed. Merging is fundamental operation. Insert is special case of merge. Delete. Min is implemented by merge. Worst-case running time of heap operations is O(n). Worst-case running time of m consecutive operations is O(m log n). Programming, Data Structures and Algorithms (Priority Queues) Slide 41/53

Binomial Queues q Leftist and skew heaps support merging, insertion and Delete. Min all effectively in O(log n) time per operation. q Binary heaps support insertion in constant average time. q Binomial queues supports all three operations in O(log n) worst-case time, insertions take constant time on average. q Binomial queues is not a heap-ordered tree but rather a collection of heap-ordered trees, known as forest. q Each heap-ordered tree satisfies a constrained form known as a binomial tree. Programming, Data Structures and Algorithms (Priority Queues) Slide 42/53

Binomial Queues q There is at most one binomial tree of every height. q A binomial tree of height 0 is a one-node tree. q A binomial tree, Bk, of height k is formed by attaching a binomial tree, Bk-1, to the root of another binomial tree Bk-1. Programming, Data Structures and Algorithms (Priority Queues) Slide 43/53

Binomial Queues q Binomial tree Bk consists of a root with B 0, B 1, …, Bk-1 subtrees. q Binomial trees of height k have exactly 2 k nodes q The number of nodes at depth d is binomial coefficient. q We impose a heap order on the binomial trees. q If we allow at most one binomial tree of any height, we can uniquely represent a priority queue of any size by a collection of binomial trees. q A priority queue of size 13 is represented by the forest B 0, B 2, and B 3 (1101). Programming, Data Structures and Algorithms (Priority Queues) Slide 44/53

Binomial Operations q Binomial queue H 1 with six elements: q The minimum element is found by scanning the root nodes of all binomial trees. § There at most log n different trees – the minimum is found in O(log n) time. q Merging two binomial queues is performed by adding two queues together § Two binomial trees of same height k are attached together and forms a binomial tree of height k+1. Programming, Data Structures and Algorithms (Priority Queues) Slide 45/53

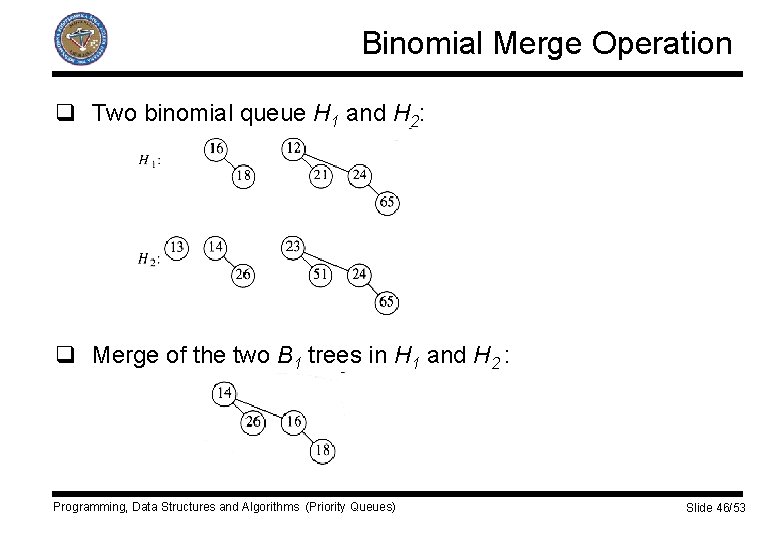
Binomial Merge Operation q Two binomial queue H 1 and H 2: q Merge of the two B 1 trees in H 1 and H 2 : Programming, Data Structures and Algorithms (Priority Queues) Slide 46/53

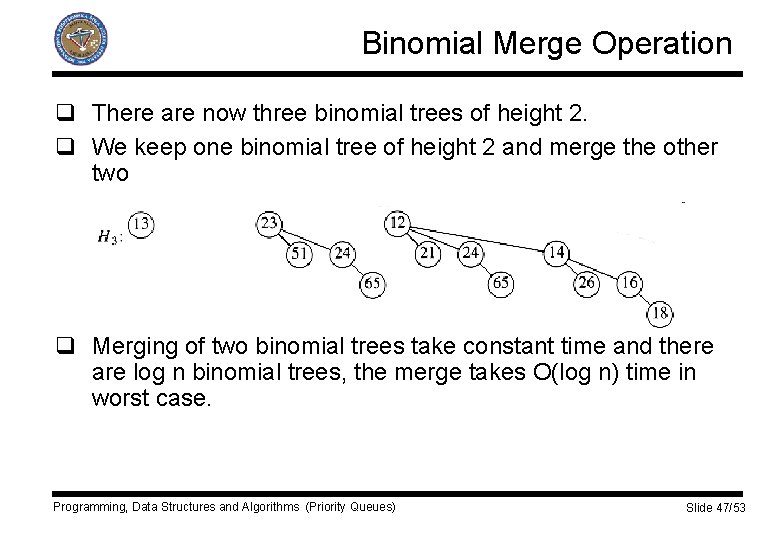
Binomial Merge Operation q There are now three binomial trees of height 2. q We keep one binomial tree of height 2 and merge the other two q Merging of two binomial trees take constant time and there are log n binomial trees, the merge takes O(log n) time in worst case. Programming, Data Structures and Algorithms (Priority Queues) Slide 47/53

Binomial Insert Operation q Insert is a special case of merge thus it takes O(log n) time in worst case. q If the priority queue does not have binomial tree Bi than the running time of the insert is proportional to i+1. q If each tree in a binomial queue is present with probability of ½, it follows that on average the insertions will terminate in two steps. q The average running time for insert is constant. q n inserts on empty binomial queue take O(n) in worst case. Programming, Data Structures and Algorithms (Priority Queues) Slide 48/53

Binomial Delete. Min Operation q First find binomial tree with smallest root node. Let it be in Bk tree. q Remove the binomial tree Bk from the priority queue H forming binomial queue H’. q Remove root node from binomial tree Bk creating binomial trees B 0, B 1, …, Bk-1, forming priority queue H’’. q Merge priority queues H’ and H’’. q It takes O(log n) time to find the tree containing minimum element and to create H’ and H’’. q Merging H’ and H’’ also takes O(log n) time q Entire Delete. Min takes O(log n) time. Programming, Data Structures and Algorithms (Priority Queues) Slide 49/53

Binomial Delete. Min Operation Programming, Data Structures and Algorithms (Priority Queues) Slide 50/53

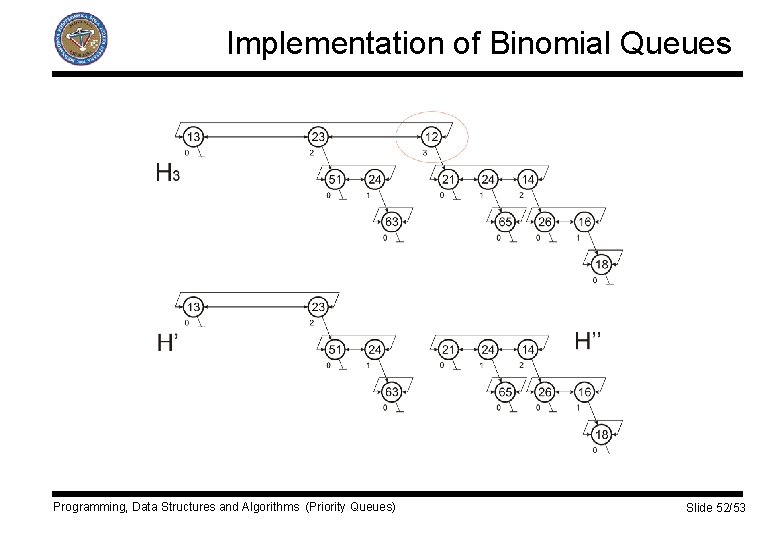
Implementation of Binomial Queues q The Delete. Min requires ability to find all the subtrees of the root quickly q Root nodes in linked list q Root node can have several children q Standard representation of general trees: § § The children are kept in a linked list. Each node has a pointer to the first child. The children are ordered by the size of their subtrees (for forming H’’) For efficient merging the size (height) of the subtree is stored in its root node. Programming, Data Structures and Algorithms (Priority Queues) Slide 51/53

Implementation of Binomial Queues Programming, Data Structures and Algorithms (Priority Queues) Slide 52/53

Binomial Queues q q q q Binomial queue is a forest Only single tree of each height Trees have 2 k elements Merging is fundamental operation. Insert is special case of merge. Delete. Min is implemented by merge. Worst-case running time of all operations is O(log n). Average-case running time of insert operation is O(1). Programming, Data Structures and Algorithms (Priority Queues) Slide 53/53