Programming Data Structures and Algorithms Graph Algorithms Anton

Programming, Data Structures and Algorithms (Graph Algorithms) Anton Biasizzo Programming, Data Structures and Algorithms (Graph Algorithms) Slide 1/63

Preliminaries q A graph G=(V, E) consists of a set of vertices, V, and a set of edges, E. q Each edge is a pair (v, w), where v, w V. q Edges are sometimes referred as arcs. q If pairs are ordered, then the graph is directed. q Directed graphs are sometimes referred as digraphs. q Vertex w is adjacent to v if and only if (v, w) E. q In undirected graph with edge (v, w), and hence (w, v), w is adjacent to v, and v is adjacent to w. q Sometimes an edge has a third component, known as either a weight or a cost. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 2/63

Preliminaries q A path in a graph is a sequence of vertices w 1, w 2, w 3, …, wn such that (wi, wi+1) E for 1≤i<n. q The length of a path is the number of edges on the path (n-1) q If the graph contains an edge (w, w) from a vertex to itself, than the path w, w is sometimes referred as a loop. We will generally consider loop-less graphs. q A simple path is a path such that all vertices are distinct, except that the first and last could be the same. q A cycle in a directed graph is a path of length least 1 such that w 1=wn; this cycle is simple if the path is simple. q For undirected graphs we require that the edges are distinct. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 3/63

Preliminaries q A directed graph is acyclic if it has no cycles (called DAG). q An undirected graph is connected, if there is a path from every vertex to every other vertex. q A directed graph with this property is called strongly connected. q If a directed graph is not strongly connected, but the underlying undirected graph is connected, then the graph is said to be weakly connected. q A complete graph is a graph in which there is an edge between every pair of vertices. q An example of real-life situation that can be modelled by graph is the airport system: airports are vertices and flights are edges. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 4/63

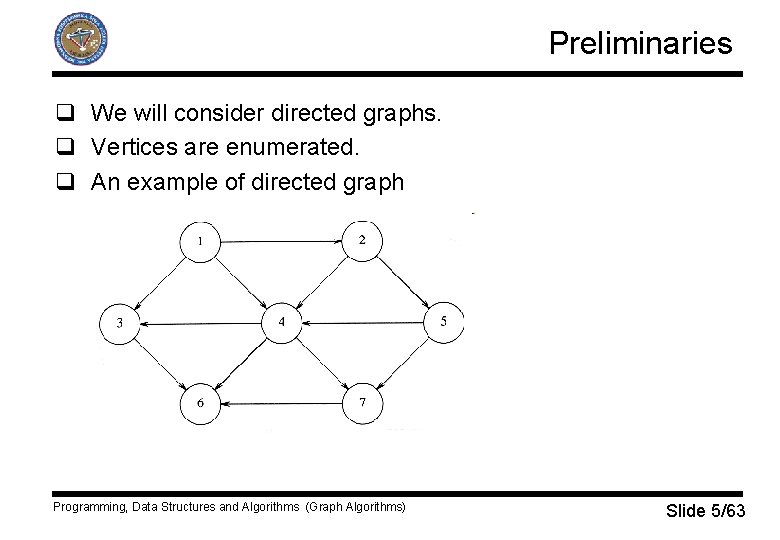
Preliminaries q We will consider directed graphs. q Vertices are enumerated. q An example of directed graph Programming, Data Structures and Algorithms (Graph Algorithms) Slide 5/63

Graph Representation q One simple way to represent a graph is to use twodimensional array, known as adjacent matrix. For each edge (u, v), we set A[u, v]=1; otherwise the entries in array are 0. q If the edge has a weight, we can set A[u, v] to the weight. q Non-existing edges could be also represented by ∞ or -∞ (for instance in the case of finding cheapest airplane route). q The space requirement is θ(|V|2), which is often prohibitive. q An adjacent matrix is an appropriate representation if the graph is dense: |E| = θ(|V|2). q In most application this is not true: the graphs are sparse. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 6/63

Sparse Graph Representation q For sparse graphs a better solution is an adjacent list representation: § For each vertex we keep a list of its adjacent vertices. q The space requirement is O(|E| + |V|). Programming, Data Structures and Algorithms (Graph Algorithms) Slide 7/63

Sparse Graph Representation q Undirected graphs are represented similarly: each edge appears in two lists, so the space usage is doubled. q A common requirement in graph algorithm is to find all vertices adjacent to some given vertex v. § This can be done in time proportional to the number of adjacent vertices by scanning the appropriate adjacent list. q In most real life applications, the vertices have names, unknown at the compile time. q The easiest way to enumerate the vertices is to use hash table, in which we store a name and internal number. q For output we need the vertex names: we can store them in separate array or keep references to the hash table. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 8/63

Problems q Topological sort. q Shortest path problem: § Unweighted edges. § Weighted edges (Dijkstra’s algorithm). § Negative weights. q Critical path problem (Earliest completion time). q Maximal network flow. q Minimum spanning tree. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 9/63

Topological Sort q A topological sort is an ordering of vertices in a directed acyclic graph, such that if there is a path from vi to vj, then vj appears after vi in the ordering. q It can be used to determine the order of courses at a university. q It is clear that a topological ordering is not possible if the graph has a cycle. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 10/63

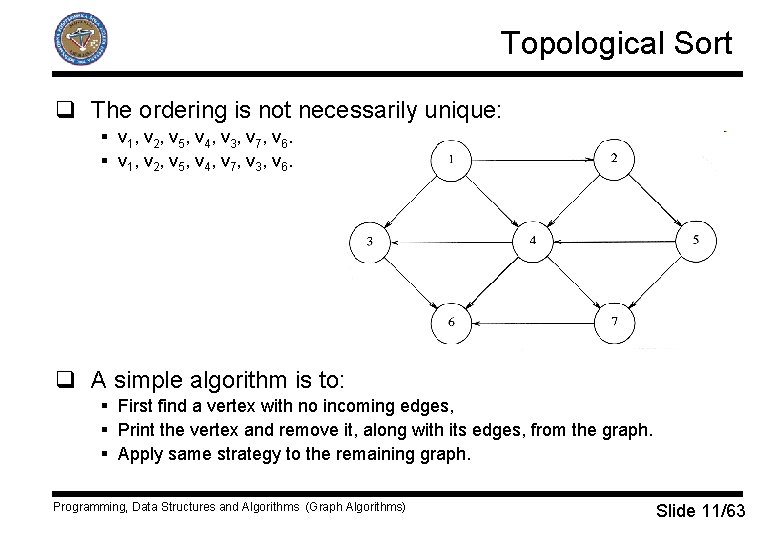
Topological Sort q The ordering is not necessarily unique: § v 1, v 2, v 5, v 4, v 3, v 7, v 6. § v 1, v 2, v 5, v 4, v 7, v 3, v 6. q A simple algorithm is to: § First find a vertex with no incoming edges, § Print the vertex and remove it, along with its edges, from the graph. § Apply same strategy to the remaining graph. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 11/63

Topological Sort q We define indegree of a vertex v as a number of incoming edges (u, v) to vertex v. q First we compute the indegree of all vertices in the graph. q Algorithm: void topsort(graph G) { unsigned int counter; vertex v, w; for ( counter=0; counter < NUM_VERTEX counter++) { v = find_new_vertex_of_indegree_zero(); if (v = NOT_A_VERTEX) error(“Graph has a cycle”); top_num[v] = counter; sorted[counter] = v; for each w adjacent to v indegree[w]--; } } Programming, Data Structures and Algorithms (Graph Algorithms) Slide 12/63

Topological Sort q Because find_new_vertex_of_indegree_zero function is a simple sequential scan of the indegree array, each call takes O(|V|) time. q Since there are |V| such calls, the running time of the algorithm is O(|V|2). q The cause of poor running time is a sequential scan. q If the graph is sparse only few vertices has their indegree changed, however, in the search of indegree 0 we look at (potentially) all the vertices. q We can remove the inefficiency by keeping all the vertices of indegree 0 in special box. When we decrement the indegree, we check if indegree falls to 0 an if so, put the vertex in the box. q The box can be implemented by either queue or stack. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 13/63

Topological Sort void topsort(graph G) { QUEUE Q; unsigned int counter; vertex v, w; Q = create_queue(NUM_VERTEX); make_null(Q); counter = 0; for each vertex v if (indegree[v] == 0) enqueue(v, Q); while ( ! Is_empty(Q) ) { v = dequeue(Q); sorted[counter] = v; top_num[v] = ++counter; for each w adjacent to v if (--indegree[w] == 0) enqueue( w, Q ); } dispose_queue( Q ); } q q Running time for this algorith is O(|E|+|V|) if adjacent lists are used. The body of for loop is executed at most once per edge. q The queue operations are done at most once per vertex. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 14/63

Shortest Path Algorithms q The input is a weighted graph. q Associated with each edge (vi, vj) is a cost ci, j to traverse the arc. q The cost of path v 1, v 2, , , v. N is q This is referred as weighted path length. q Single source shortest path problem: § Given as input a weighted graph, G=(V, E), and a distinguished vertex, s, find the shortest weighted path from s to every other vertex in G. q If graph have negative edges, there could be negative loops and shortest path are not defined. q Many practical examples of shortest path problem: § Communication in the network, § Airplane or other transit routes, … Programming, Data Structures and Algorithms (Graph Algorithms) Slide 15/63

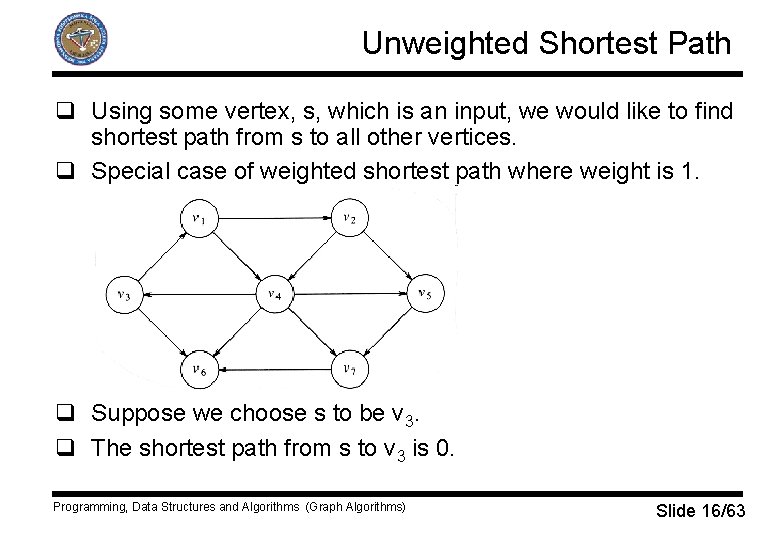
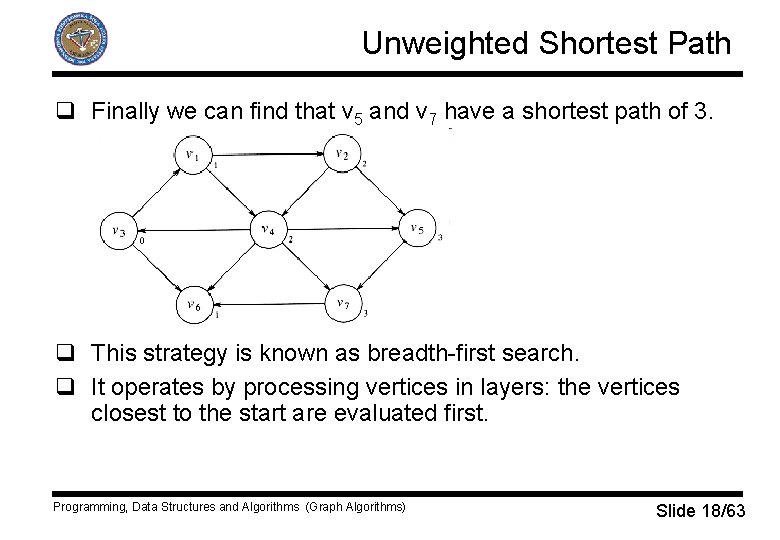
Unweighted Shortest Path q Using some vertex, s, which is an input, we would like to find shortest path from s to all other vertices. q Special case of weighted shortest path where weight is 1. q Suppose we choose s to be v 3. q The shortest path from s to v 3 is 0. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 16/63

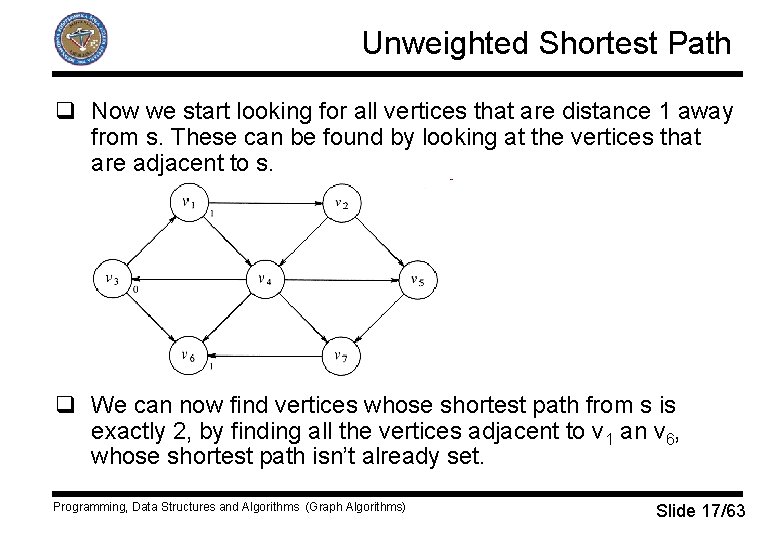
Unweighted Shortest Path q Now we start looking for all vertices that are distance 1 away from s. These can be found by looking at the vertices that are adjacent to s. q We can now find vertices whose shortest path from s is exactly 2, by finding all the vertices adjacent to v 1 an v 6, whose shortest path isn’t already set. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 17/63

Unweighted Shortest Path q Finally we can find that v 5 and v 7 have a shortest path of 3. q This strategy is known as breadth-first search. q It operates by processing vertices in layers: the vertices closest to the start are evaluated first. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 18/63

Unweighted Shortest Path q For each vertex we keep track of: § Its distance from s in the entry dv. § The entry pv is for bookkeeping variable to keep track of path. § The entry Known is set to 1 after vertex is processed. q Initial configuration of table: v v 1 v 2 v 3 v 4 v 5 v 6 v 7 Known 0 0 0 0 dv ∞ ∞ 0 ∞ ∞ pv 0 0 0 0 Programming, Data Structures and Algorithms (Graph Algorithms) Slide 19/63

Unweighted Shortest Path q Algorithm: § For distances from 0 to Num. Vertex-1 find unprocessed vertex with current distance. § Mark it as processed. § For all adjacent vertices of the current vertex, whose distance isn’t already set o set the distance of adjacent vertex w to current distance + 1 o set previous vertex field pv of adjacent vertex w to current vertex v. q Actual path can be determined by backtracking through variable pv. q The running time is O(|V|2) because of doubly nested loops. q Inefficiency is due to search over whole set of vertices even when they become known. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 20/63

Unweighted Shortest Path q At any point we have two types of unknown vertices that have already set distance: § Vertices with distance dv=current_distance + 1. q Simple solution would be to keep these vertices in two boxes, one for each distance: § We took vertices from first box with current distance. § We set the distance of unprocessed adjacent vertices to current distance + 1 and put them to second box. q We could refine this approach by using only single queue, since the adjacent vertices with incremented distance are enqueued at the rear. q The running time of improved algorithm is O(|V|+|E|). Programming, Data Structures and Algorithms (Graph Algorithms) Slide 21/63

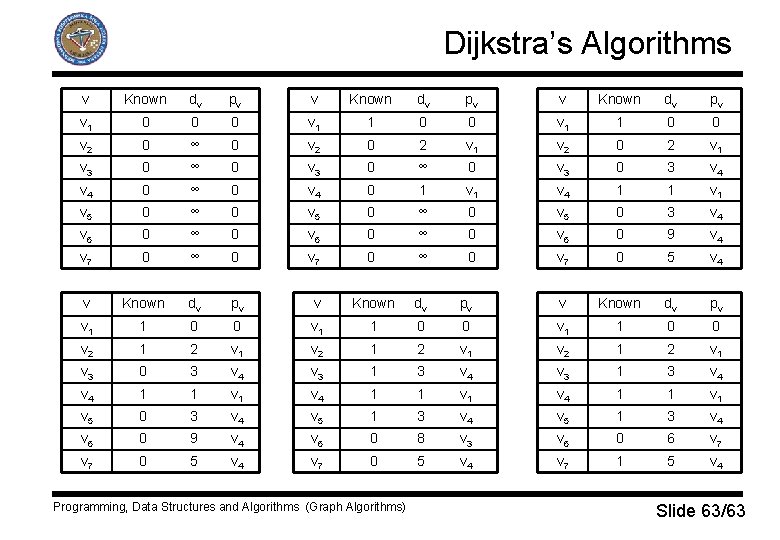
Dijkstra’s Algorithms q If the graph is weighted the problem becomes harder. q We keep the same information as before. q The general method to solve the single source shortest path problem is known a Dijkstra’s algorithm, q It is greedy algorithm, that solves a problem in stages by doing what appears to be the best thing at each stage. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 22/63

Dijkstra’s Algorithms q Dijkstra’s algorithm: While set of unknown vertices is not empty do: § Select a vertex v, which has smallest distance dv from the set of unknown vertices. § Mark the selected vertex v as known. § For all adjacent vertices if current distance dw is bigger than dv + cv, w o adjust its distance dw to dv + cv, w, . o set previous vertex field pv of the adjacent vertex w to current vertex v. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 23/63

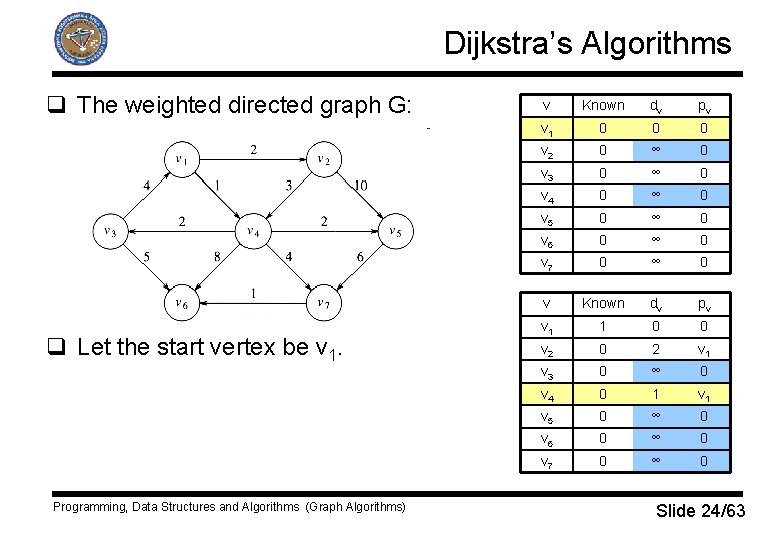
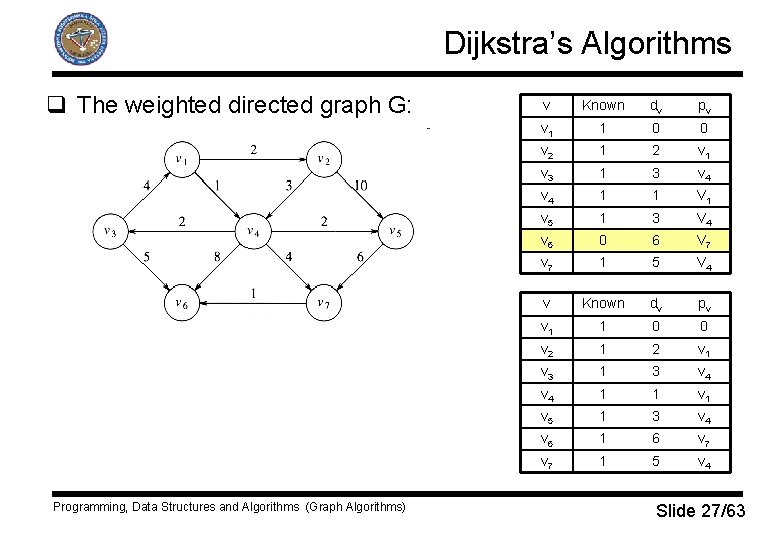
Dijkstra’s Algorithms q The weighted directed graph G: q Let the start vertex be v 1. Programming, Data Structures and Algorithms (Graph Algorithms) v Known dv pv v 1 0 0 0 v 2 0 ∞ 0 v 3 0 ∞ 0 v 4 0 ∞ 0 v 5 0 ∞ 0 v 6 0 ∞ 0 v 7 0 ∞ 0 v Known dv pv v 1 1 0 0 v 2 0 2 v 1 v 3 0 ∞ 0 v 4 0 1 v 5 0 ∞ 0 v 6 0 ∞ 0 v 7 0 ∞ 0 Slide 24/63

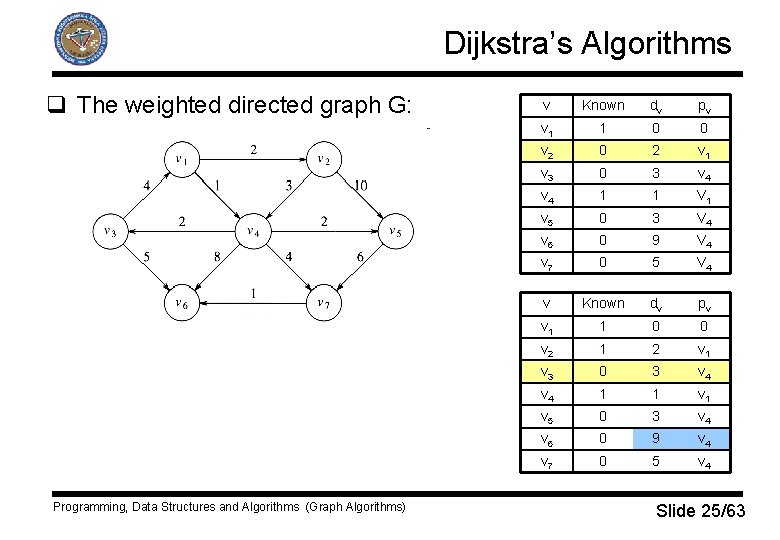
Dijkstra’s Algorithms q The weighted directed graph G: Programming, Data Structures and Algorithms (Graph Algorithms) v Known dv pv v 1 1 0 0 v 2 0 2 v 1 v 3 0 3 v 4 1 1 V 1 v 5 0 3 V 4 v 6 0 9 V 4 v 7 0 5 V 4 v Known dv pv v 1 1 0 0 v 2 1 2 v 1 v 3 0 3 v 4 1 1 v 5 0 3 v 4 v 6 0 9 v 4 v 7 0 5 v 4 Slide 25/63

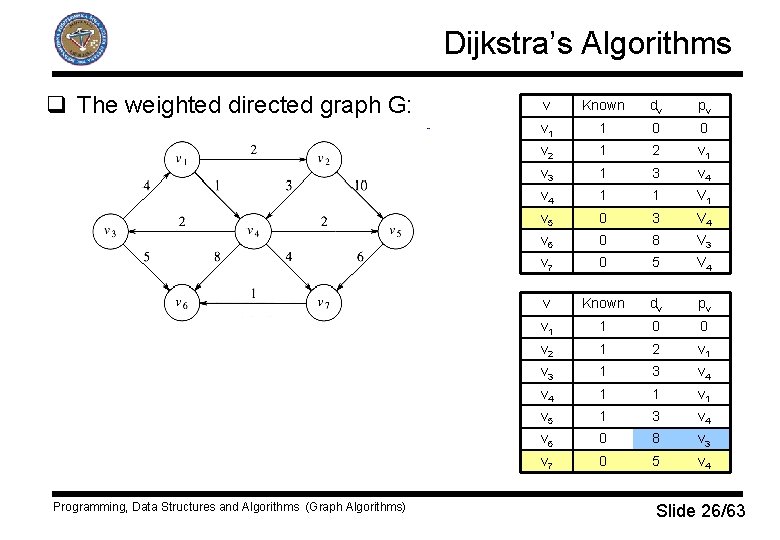
Dijkstra’s Algorithms q The weighted directed graph G: Programming, Data Structures and Algorithms (Graph Algorithms) v Known dv pv v 1 1 0 0 v 2 1 2 v 1 v 3 1 3 v 4 1 1 V 1 v 5 0 3 V 4 v 6 0 8 V 3 v 7 0 5 V 4 v Known dv pv v 1 1 0 0 v 2 1 2 v 1 v 3 1 3 v 4 1 1 v 5 1 3 v 4 v 6 0 8 v 3 v 7 0 5 v 4 Slide 26/63

Dijkstra’s Algorithms q The weighted directed graph G: Programming, Data Structures and Algorithms (Graph Algorithms) v Known dv pv v 1 1 0 0 v 2 1 2 v 1 v 3 1 3 v 4 1 1 V 1 v 5 1 3 V 4 v 6 0 6 V 7 v 7 1 5 V 4 v Known dv pv v 1 1 0 0 v 2 1 2 v 1 v 3 1 3 v 4 1 1 v 5 1 3 v 4 v 6 1 6 v 7 1 5 v 4 Slide 27/63

Dijkstra’s Algorithms q A Dijkstra’s algorithm works only for non-negative weights. q The running time depends on how the table is manipulated. q If we use obvious algorithm of scanning down the table to find the minimum dv, each phase will take O(|V|) time to find the minimum, and thus O(|V|2) will be spent for whole algorithm. q The time for updating dw is constant per update, and there must be at most one update per edge for a total of O(|E|). q Total running time is O(|E|+|V|2). q If the graph is dense, with |E| = θ(|V|2), then this algorithm is optimal. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 28/63

Dijkstra’s Algorithms q If the graph is sparse, with |E| = θ(|V|), this algorithm is too slow. q Vertices with their distances as keys could be kept in priority queue. q There are two ways of managing the change of value of dw: § Find the distance to be decreased in the queue, decrease it and update the queue. Since Find operation in priority queues are difficult this is an ugly solution. § Enqueue a copy of vertex with decreased distance. This instance will be processed first since it has lower distance. At reading smallest unprocessed distance we need to verify that the vertex hasn’t been already processed. q The running time requirement is O(|E| log |V|). Programming, Data Structures and Algorithms (Graph Algorithms) Slide 29/63

Negative Edge Costs q Dijkstra’s algorithm does not work: § Some vertex u is declared known. § It is possible that from some unknown vertex v there is a negative path to vertex u. § A path from source s to v and back to u might be better. q Allow algorithm to “change its mind”: § Dismiss the concept of known vertices. q Place start vertex s on queue q At each stage: § Dequeue a vertex v. § For all vertices w adjacent to vertex v such that dw>dv+cv, w: o Update dw and pw. o Place w on a queue, if it is not already there (use a bit at vertex as an indicator). q Finish when queue is empty. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 30/63

Negative Edge Costs q Each vertex can be dequeued at most |V| times. q Running time is O(|E| |V|) if adjacent lists are used. § Quite an increase from Dijkstra’s algorithm. q If negative-cost cycles are present, then the algorithm will loop indefinitely. q We can stop the algorithm after any vertex has dequeued |V|+1 times. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 31/63

Acyclic graphs q q If the graph is acyclic, we can improve Dijkstra’s algorithm. Change the order in which vertices are declared known: Vertex selection rule – select vertices in topological order. Algorithm can be done in one pass, since selections and updates can take place as the topological sort is being performed. q The selection rule works because when a vertex v is selected, its distance, dv, can no longer be lowered, because it has no incoming edges from unknown vertices. q Priority queue is not needed. q Running time is O(|E| + |V|). Programming, Data Structures and Algorithms (Graph Algorithms) Slide 32/63

Acyclic graphs q Acyclic graphs models: § downhill skiing problem, § nonreversible chemical reactions, § critical path analysis. q Critical path analysis (activity-node graph): § Each node represents an activity, that must be performed along with the time required for the operation. § The edges represent precedence relationships. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 33/63

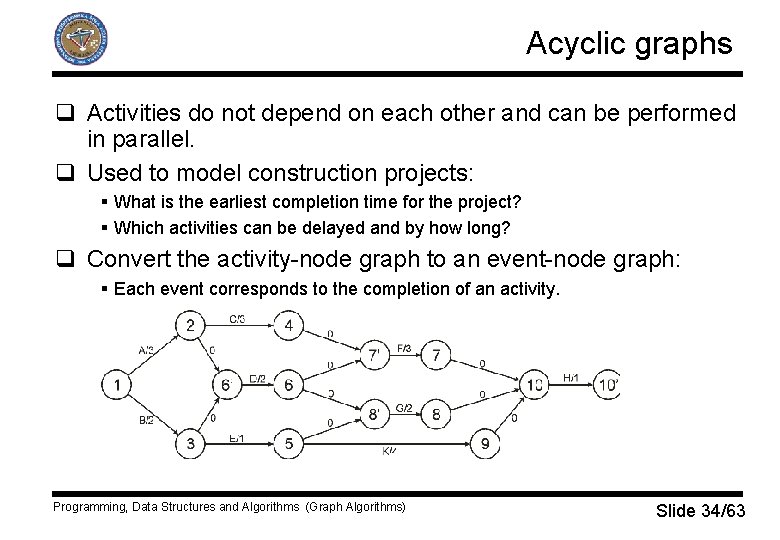
Acyclic graphs q Activities do not depend on each other and can be performed in parallel. q Used to model construction projects: § What is the earliest completion time for the project? § Which activities can be delayed and by how long? q Convert the activity-node graph to an event-node graph: § Each event corresponds to the completion of an activity. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 34/63

Acyclic graphs q Earliest completion time – find the longest path from the first event to the last event. q In general graphs there are possible positive-cost cycles – longest path does not make sense q The event-node graph is acyclic. q Adaptation of the shortest path problem: § If ECi is the earliest completion time for node (event) i, then rules are: q Latest time, LCi, that each event can finish without affecting the final completion time: Programming, Data Structures and Algorithms (Graph Algorithms) Slide 35/63

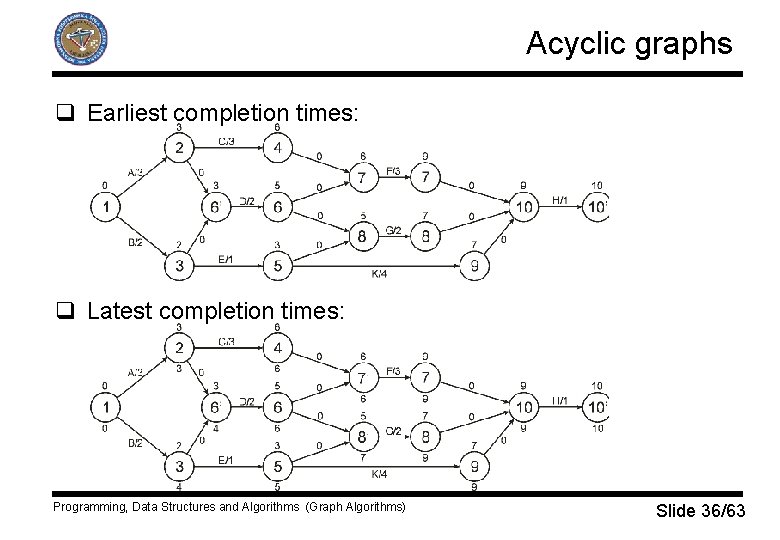
Acyclic graphs q Earliest completion times: q Latest completion times: Programming, Data Structures and Algorithms (Graph Algorithms) Slide 36/63

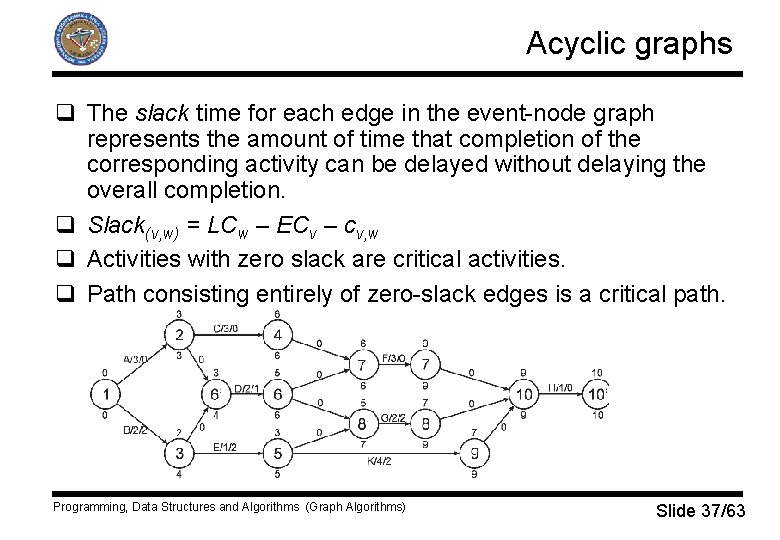
Acyclic graphs q The slack time for each edge in the event-node graph represents the amount of time that completion of the corresponding activity can be delayed without delaying the overall completion. q Slack(v, w) = LCw – ECv – cv, w q Activities with zero slack are critical activities. q Path consisting entirely of zero-slack edges is a critical path. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 37/63

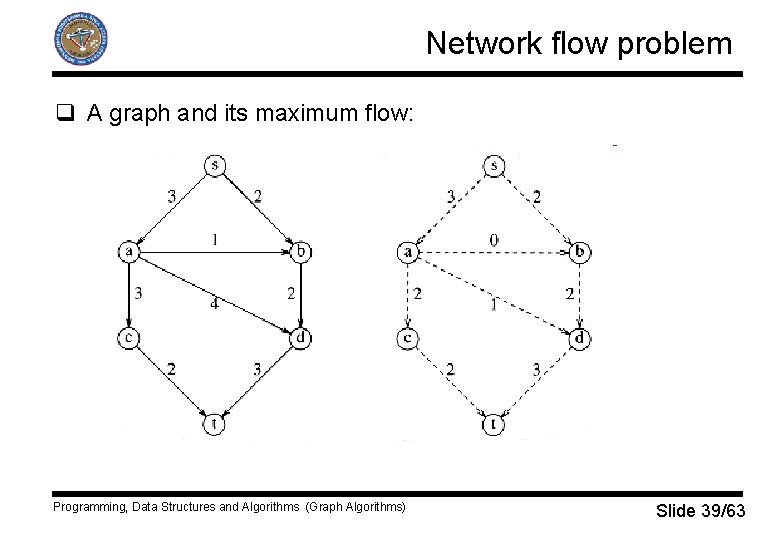
Network flow problem q Suppose we have a directed graph G=(V, E) with edge capacities cv, w. q Capacities could represent: § the water flow in pipes, § the amount of traffic that can flow between two intersections, § network flow, … q We have two special vertices: § the source s, and the sink t. q Through edge (v, w), at most cv, w units of “flow” may pass. q At any vertex that is not source nor sink, the total flow coming in must equal to the total flow going out: § continuity equation q Determine the maximum amount of flow that can pass from source s to sink t. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 38/63

Network flow problem q A graph and its maximum flow: Programming, Data Structures and Algorithms (Graph Algorithms) Slide 39/63

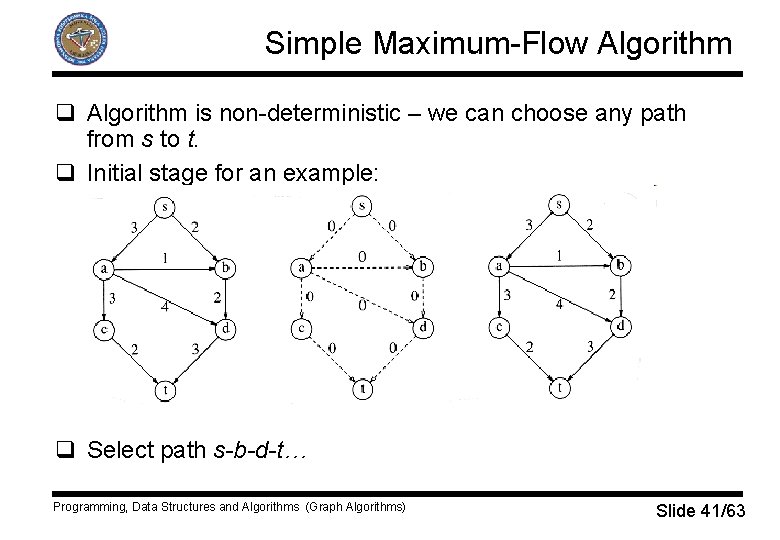
Simple Maximum-Flow Algorithm q Solve the problem in stages. q Start with graph G. q Construct a flow graph Gf that tells the flow that has been attained at any stage. Initially all edges in Gf have no flow. q Construct residual graph Gr, that tells for each edge how much more flow can be added. We subtract the current flow from the capacity. q At each stage, find a path in residual graph Gr from s to t – augmenting path. q The minimum edge on this path is the amount of flow that can be added to every edge on the path in the flow graph. q Adjust Gf an recompute Gr. q Terminate when there is no path from s to t in Gr. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 40/63

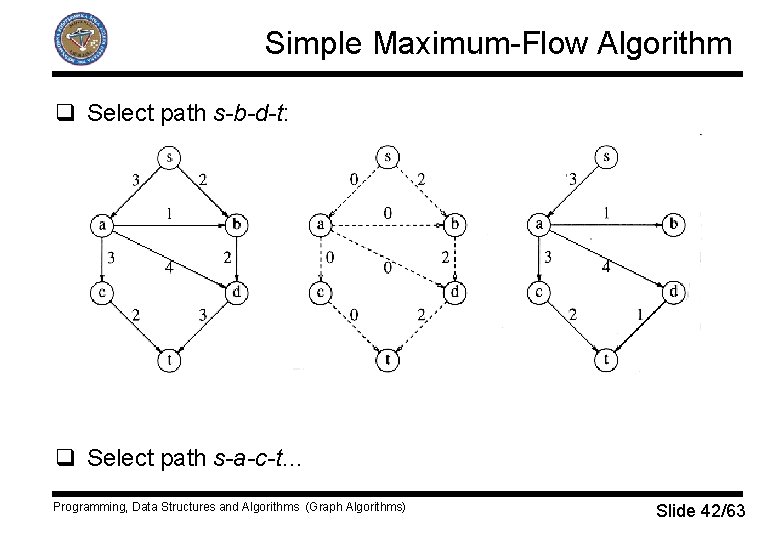
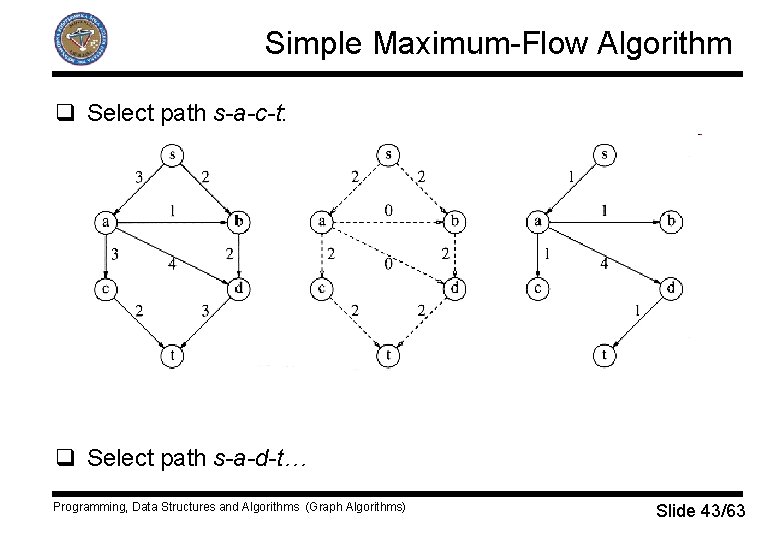
Simple Maximum-Flow Algorithm q Algorithm is non-deterministic – we can choose any path from s to t. q Initial stage for an example: q Select path s-b-d-t… Programming, Data Structures and Algorithms (Graph Algorithms) Slide 41/63

Simple Maximum-Flow Algorithm q Select path s-b-d-t: q Select path s-a-c-t… Programming, Data Structures and Algorithms (Graph Algorithms) Slide 42/63

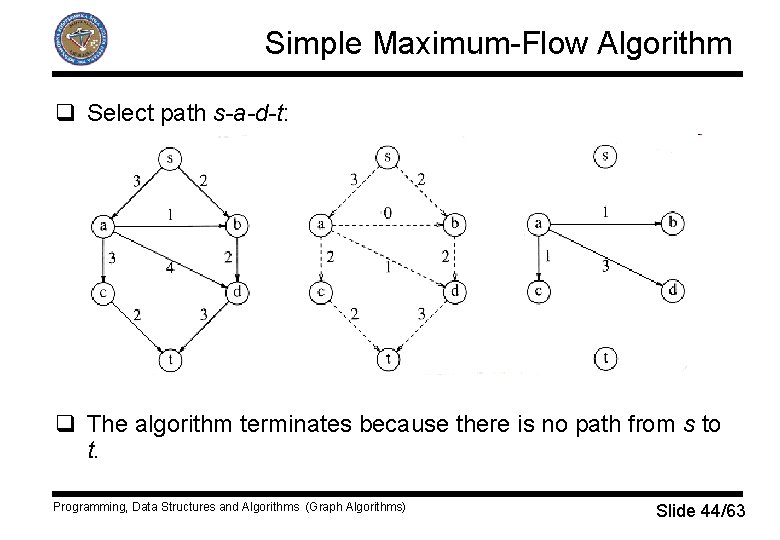
Simple Maximum-Flow Algorithm q Select path s-a-c-t: q Select path s-a-d-t… Programming, Data Structures and Algorithms (Graph Algorithms) Slide 43/63

Simple Maximum-Flow Algorithm q Select path s-a-d-t: q The algorithm terminates because there is no path from s to t. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 44/63

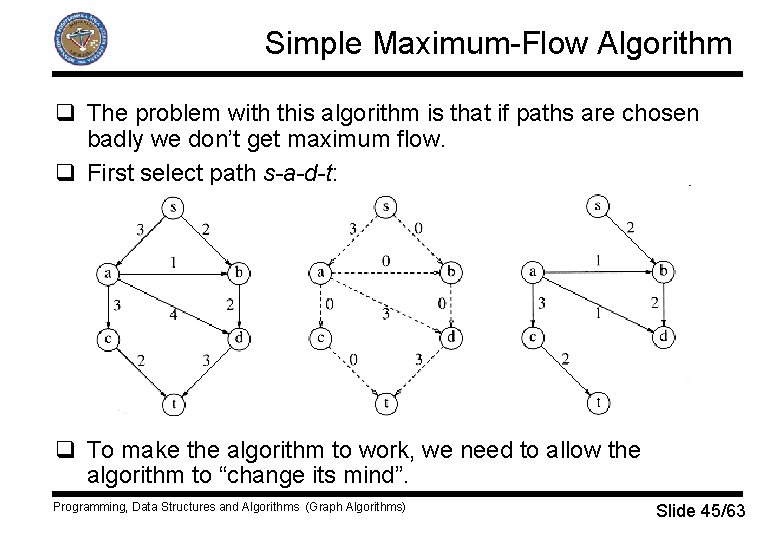
Simple Maximum-Flow Algorithm q The problem with this algorithm is that if paths are chosen badly we don’t get maximum flow. q First select path s-a-d-t: q To make the algorithm to work, we need to allow the algorithm to “change its mind”. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 45/63

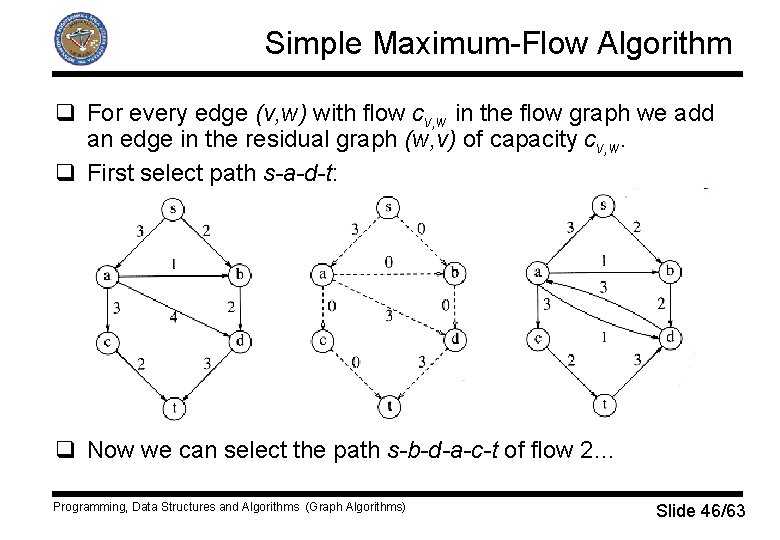
Simple Maximum-Flow Algorithm q For every edge (v, w) with flow cv, w in the flow graph we add an edge in the residual graph (w, v) of capacity cv, w. q First select path s-a-d-t: q Now we can select the path s-b-d-a-c-t of flow 2… Programming, Data Structures and Algorithms (Graph Algorithms) Slide 46/63

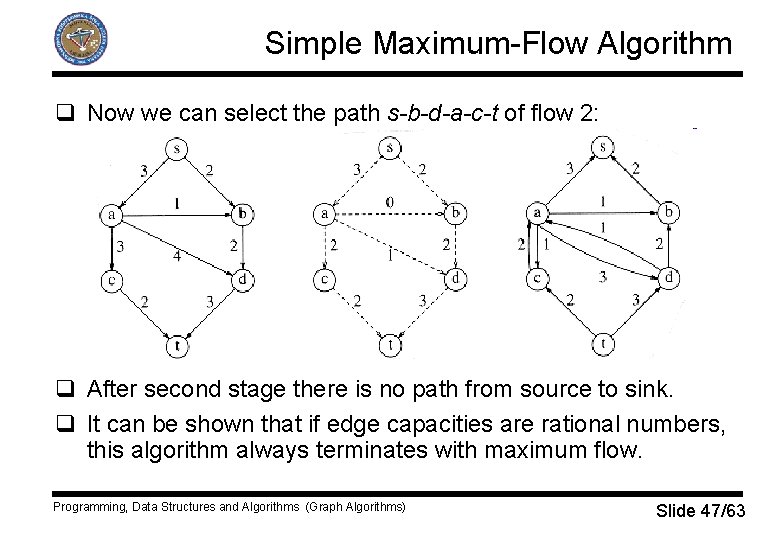
Simple Maximum-Flow Algorithm q Now we can select the path s-b-d-a-c-t of flow 2: q After second stage there is no path from source to sink. q It can be shown that if edge capacities are rational numbers, this algorithm always terminates with maximum flow. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 47/63

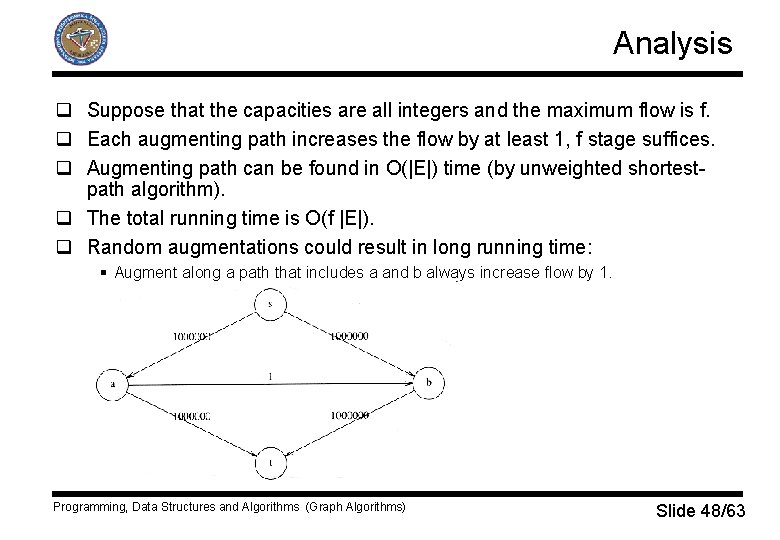
Analysis q Suppose that the capacities are all integers and the maximum flow is f. q Each augmenting path increases the flow by at least 1, f stage suffices. q Augmenting path can be found in O(|E|) time (by unweighted shortestpath algorithm). q The total running time is O(f |E|). q Random augmentations could result in long running time: § Augment along a path that includes a and b always increase flow by 1. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 48/63

Maximum-Flow Algorithm q Simple solution is to always choose the augmenting path that allows the largest increase in flow. § This is similar to solving weighted shortest-path problem. § Running time is O(|E|2 log|V|) if the capacitances are small integers. q Another possibility is to choose augmenting path with fewest number of edges. § The running time is O(E|2 |V|) q There are several, more complicated, algorithms, which have data structure improvements. q Currently best-known bound is O(|E||V| log(|V|2/|E|)). q There a lot of very good bounds for special cases: § O(|E| |V|1/2 ) time bound algorithm for graphs where except the source and the sink all vertices have either a single incoming or single outgoing edge of capacity 1. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 49/63

Minimum Spanning Tree q We will consider problem of finding a minimum spanning tree in an undirected graph. q Finding a minimum spanning tree in a directed graph is more difficult. q Minimum spanning tree of an undirected graph G is a tree formed from graph edges that connects all the vertices of G at lowest total cost. q We will assume the graph G is connected. q For any spanning tree T, if an edge e, that is not in T is added, a cycle is created. q The removal of any edge on the cycle reinstates the spanning tree property. q The cost of the spanning tree is lowered if added edge has lower cost than the edge that was removed. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 50/63

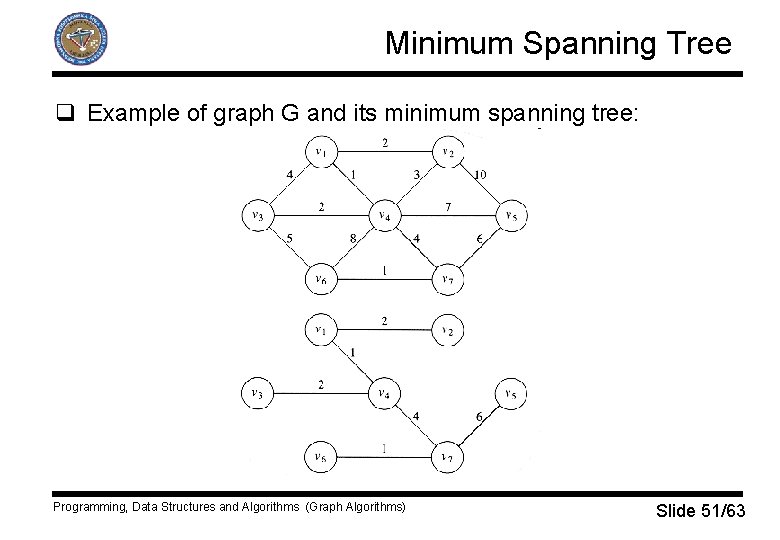
Minimum Spanning Tree q Example of graph G and its minimum spanning tree: Programming, Data Structures and Algorithms (Graph Algorithms) Slide 51/63

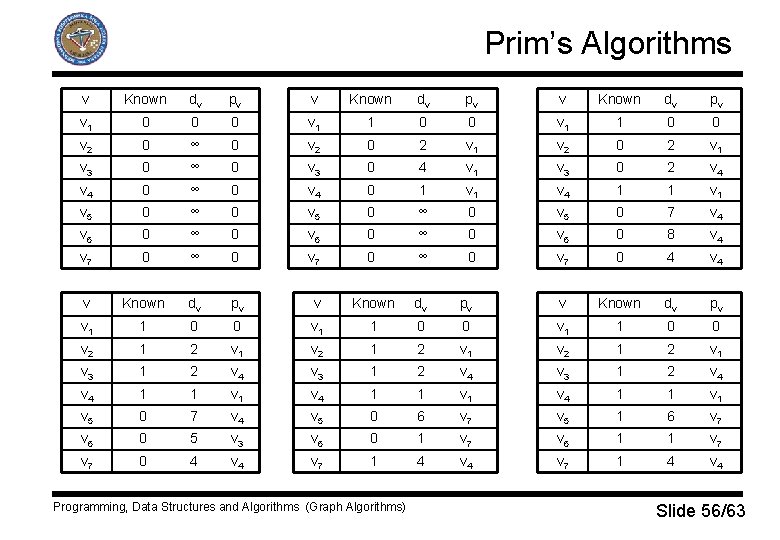
Prim’s Algorithm q One way to compute the minimum spanning tree is to grow the tree in successive stage. q In each stage, one node is picked as the root, and an edge is added, and an associated vertex, to the tree. q At any point in the algorithm, we have a set of vertices that have already been included in the tree; the rest of the vertices have not. q At each stage the algorithm finds a new vertex to add to the tree, by choosing the edge (u, v) such that the cost of (u, v) is the smallest among all edges where u is in the tree and v is not. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 52/63

Prim’s Algorithm q Prim’s algorithm is similar to Dijkstra’s algorithm for the shortest paths. q For each vertex v we keep values dv and pv and indication if vertex is known. q dv is the weight of the shortest arc connecting v to a known vertex. q pv is the last vertex to cause the change in dv. q The rest of the algorithm is the same as Dijkstra’s algorithm with exception of the update rule: § After a vertex v is selected, for each unknown w adjacent to v, dw = min(dw, cw, v). Programming, Data Structures and Algorithms (Graph Algorithms) Slide 53/63

Prim’s Algorithm q Prim’s algorithm: While set of unknown vertices is not empty do: § Select a vertex v, which has smallest weight dv from the set of unknown vertices. § Mark the selected vertex v as known. § For all adjacent vertices w update its weight dw to cw, v if current weight dw is bigger than cw, v. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 54/63

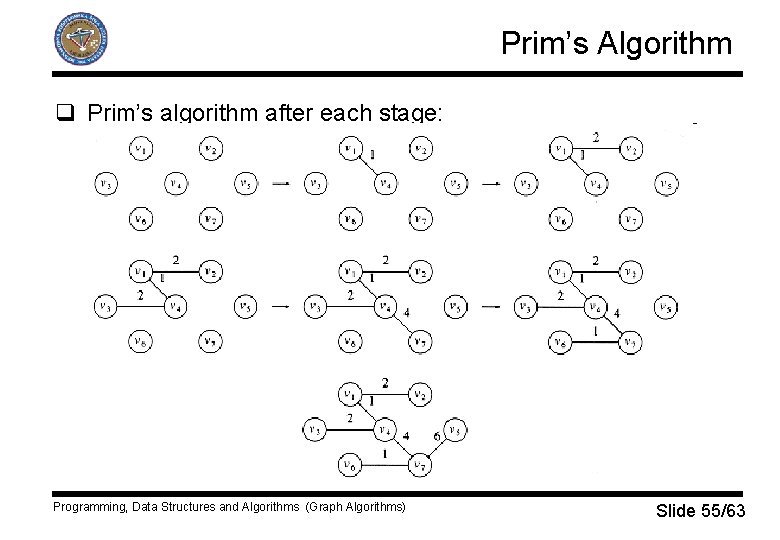
Prim’s Algorithm q Prim’s algorithm after each stage: Programming, Data Structures and Algorithms (Graph Algorithms) Slide 55/63

Prim’s Algorithms v Known dv pv v 1 0 0 0 v 1 1 0 0 v 2 0 ∞ 0 v 2 0 2 v 1 v 3 0 ∞ 0 v 3 0 4 v 1 v 3 0 2 v 4 0 ∞ 0 v 4 0 1 v 4 1 1 v 5 0 ∞ 0 v 5 0 7 v 4 v 6 0 ∞ 0 v 6 0 8 v 4 v 7 0 ∞ 0 v 7 0 4 v Known dv pv v 1 1 0 0 v 2 1 2 v 1 v 3 1 2 v 4 1 1 v 1 v 4 1 1 v 5 0 7 v 4 v 5 0 6 v 7 v 5 1 6 v 7 v 6 0 5 v 3 v 6 0 1 v 7 v 6 1 1 v 7 0 4 v 4 v 7 1 4 v 4 Programming, Data Structures and Algorithms (Graph Algorithms) Slide 56/63

Prim’s Algorithm q The entire implementation of Prim’s algorithm is virtually identical to that of Dijkstra’s algorithm. q The analysis of Dijkstra’s algorithm applies for Prim’s algorithm. q Prim’s algorithm runs on undirected graphs – every edge in two adjacent lists. q The running time without heaps is O(|V|2), which is optimal for dense graphs. q The running time for implementations using binary heaps, which is good for sparse graphs, is O(|E| log |V|). Programming, Data Structures and Algorithms (Graph Algorithms) Slide 57/63

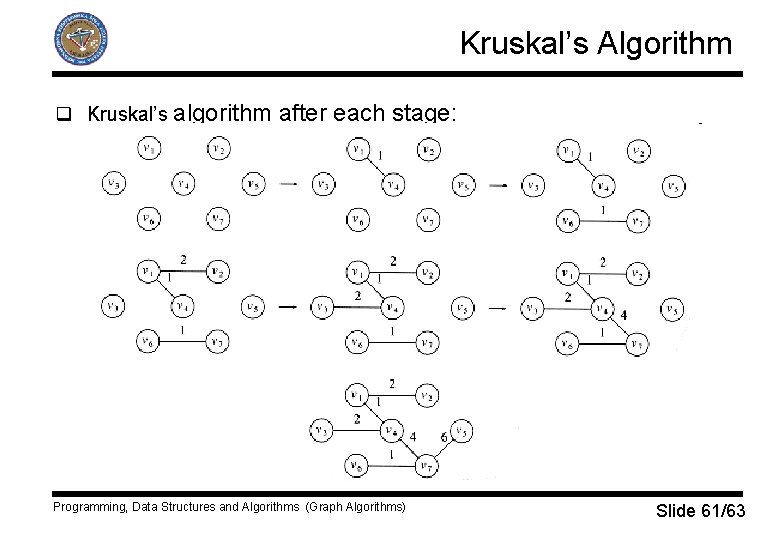
Kruskal’s Algorithm q A second greedy strategy is to continually select the edges in order of smallest weight and accept an edge if it does not cause a cycle. q Formally, Kruskal’s algorithm maintains a forest – a collection of trees. q Initially, there are |V| single-node trees. q When algorithm terminates there is only one tree – a minimum spanning tree. q The algorithm terminates when enough edges are accepted. q The sets with Union/Find algorithm is appropriate data structure. q Two vertices belongs to the same set if and only if they are connected. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 58/63

Kruskal’s Algorithm q Initially, each vertex is in its own set. q If u and v are in the same set, the edge (u, v) is rejected. § Adding (u, v) would cause a cycle. q Otherwise the edge (u, v) is accepted, and a Union operation is performed on two sets containing u and v. q The edges could be sorted, but building a heap in linear time is much better. q Then the Delete. Min give the edge to be tested in order. q Typically, only a small fraction of the edges need to be tested, although it is possible that all the edges must be tried. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 59/63

Kruskal’s Algorithm q Actions of Kruskal’s algorithm on G: Edge Weight Action (v 1, v 4) 1 Accepted (v 6, v 7) 1 Accepted (v 1, v 2) 2 Accepted (v 3, v 4) 2 Accepted (v 2, v 4) 3 Rejected (v 1, v 3) 4 Rejected (v 4, v 7) 4 Accepted (v 3, v 6) 5 Rejected (v 5, v 7) 6 Accepted Programming, Data Structures and Algorithms (Graph Algorithms) Slide 60/63

Kruskal’s Algorithm q Kruskal’s algorithm after each stage: Programming, Data Structures and Algorithms (Graph Algorithms) Slide 61/63

Kruskal’s Algorithm q The worst case running time is O(|E| log |E|). q Since |E| = O(|V|2), the running time is O(|E| log |V|). q In practice, the algorithm is much faster then this bound indicates. Programming, Data Structures and Algorithms (Graph Algorithms) Slide 62/63

Dijkstra’s Algorithms v Known dv pv v 1 0 0 0 v 1 1 0 0 v 2 0 ∞ 0 v 2 0 2 v 1 v 3 0 ∞ 0 v 3 0 3 v 4 0 ∞ 0 v 4 0 1 v 4 1 1 v 5 0 ∞ 0 v 5 0 3 v 4 v 6 0 ∞ 0 v 6 0 9 v 4 v 7 0 ∞ 0 v 7 0 5 v 4 v Known dv pv v 1 1 0 0 v 2 1 2 v 1 v 3 0 3 v 4 v 3 1 3 v 4 1 1 v 1 v 4 1 1 v 5 0 3 v 4 v 5 1 3 v 4 v 6 0 9 v 4 v 6 0 8 v 3 v 6 0 6 v 7 0 5 v 4 v 7 1 5 v 4 Programming, Data Structures and Algorithms (Graph Algorithms) Slide 63/63