Programming Abstractions for Approximate Computing Michael Carbin with

Programming Abstractions for Approximate Computing Michael Carbin with Sasa Misailovic, Hank Hoffmann, Deokhwan Kim, Stelios Sidiroglou, Martin Rinard

Challenges for Programming • Expression (specifying approximations) • Reasoning (verifying resulting program) • Debugging (reproducing failures) • Deployment (changes in assumptions)

Fundamental Questions • Scope • What do we approximate and how? • Specifications of “Correctness” • What is correctness? • Reasoning • How do we reason about correctness?

[Misailovic, Carbin, Achour, Qi, Rinard MIT-TR 14] What do we approximate? • Domains have inherent uncertainty Benchmark Domain LOC (Kernel) Time in Kernel (%) sor numerical 173 23 82. 30% blackscholes finance 494 88 65. 11% dct 532 62 99. 20% 532 93 98. 86% 218 88 93. 43% idct scale image processing • Execution time dominated by a fraction of code

• Approximation Transformations Approximate Hardware PCMOS, Palem et al. 2005; Narayanan et al. , DATE ’ 10; Liu et al. ASPLOS ’ 11; Sampson et al, PLDI ’ 11; Esmaeilzadeh et al. , ASPLOS ’ 12, MICRO’ 12 • Function Substitution Hoffman et al. , APLOS ’ 11; Ansel et al. , CGO ’ 11; Zhu et al. , POPL ‘ 12 • Approximate Memoization Alvarez et al. , IEEE TOC ’ 05; Chaudhuri et al. , FSE ’ 12; Samadi et al. , ASPLOS ’ 14 • Relaxed Synchronization (Lock Elision) Renganarayana et al. , RACES ’ 12; Rinard, Hot. Par ‘ 13; Misailovic, et al. , RACES ’ 12 • Code Perforation Rinard, ICS ‘ 06; Baek et al. , PLDI 10; Misailovic et al. , ICSE ’ 10;

Example: Loop Perforation float sum = 0; for (int i = 0; i < n; i += 1) { sum = sum + a[i]; } float avg = sum / n;

Example: Loop Perforation float sum = 0; for (int i = 0; i < n; i += 1) { sum = sum + a[i]; i += 2 } float avg = sum / n; float avg = (sum * 2) / n; • Skip iterations (or truncate or random subset) • Potentially add extrapolations to reduce bias

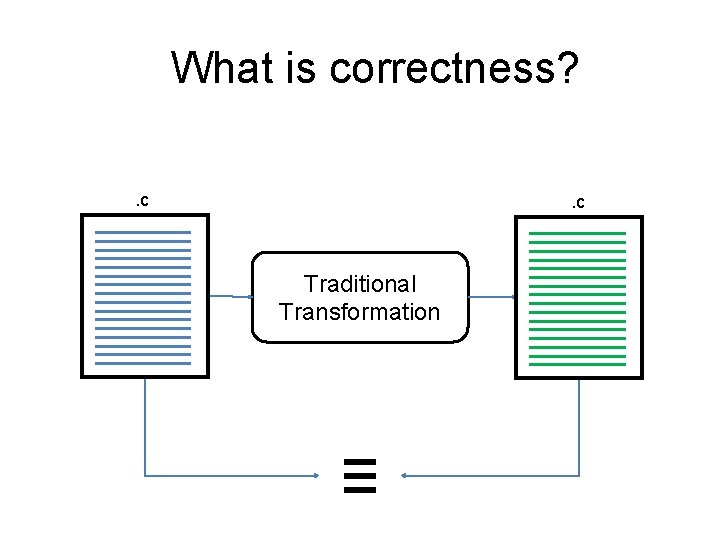
What is correctness? . c Traditional Transformation ≡

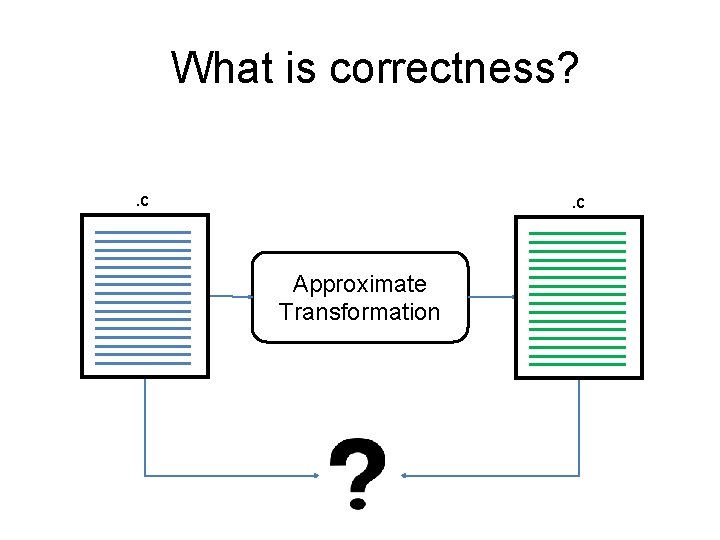
What is correctness? . c Approximate Transformation

What is correctness? • Safety: satisfies standard unary assertions (type safety, memory safety, partial functionality) • Accuracy: program satisfies relational assertions that constrain difference in results

Relational Assertions • Contribution: program logic and verification system that supports verifying relationships between implementations relate |x<o> - x<a>| / x<o> <=. 1; • x<o>: value of x in original implementation • x<a>: value of x in approximate implementation [Carbin, Kim, Misailovic, Rinard PLDI’ 12, PEP

Example: Loop Perforation float sum = 0; for (int i = 0; i < n; i += 1) { sum = sum + a[i]; i += 2 } float avg = sum / n; float avg = (sum * 2) / n;

Example: Loop Perforation float sum = 0; for (int i = 0; i < n; i += 1) { sum = sum + a[i]; i += 2 } float avg = sum / n; float avg = (sum * 2) / n; • Worst-case error:

Novel Safety Verification Concept • Assume validity of assertions in original program • Use relations to prove that approximation does not change validity of assertions p<o> == p<a> ∧ safe(*p<o>) safe(*p<a>) assert (safe(*p)) • Lower verification complexity than verifying an assertion outright

Specifications and Reasoning • Worst-case (for all inputs) • • • Non-interference [Sampson et al. , PLDI ‘ 11] Assertions [Carbin et al. , PLDI ‘ 12; PEPM ‘ 13] Accuracy [Carbin et al. , PLDI ‘ 12] • Statistical (with some probability) • • Assertions [Sampson et al. , PLDI ‘ 14] Reliability [Carbin, Misailovic, and Rinard, OOPSLA ‘ 13] Expected Error [Zhu, Misailovic et al. , POPL ‘ 13] Probabilistic Error Bounds [Misailovic et al. , SAS ‘ 13]

Questions from Computer Science

Question #1: “Programmers will never do this. ” - Unnamed Systems and PL Researchers

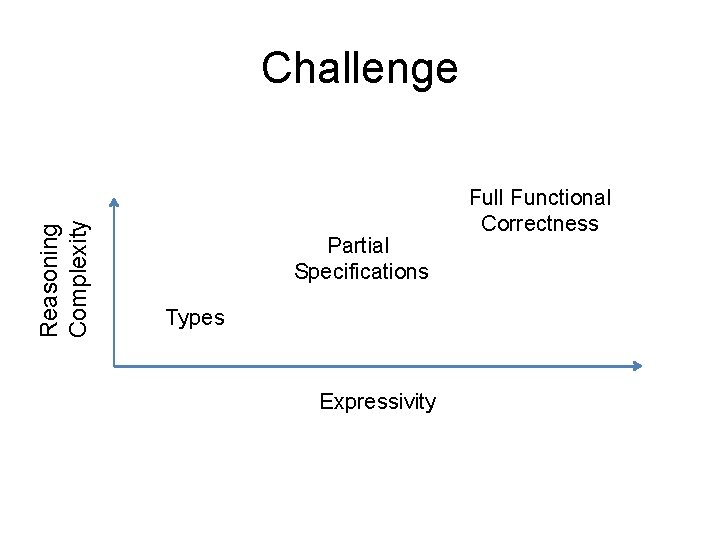
Reasoning Complexity Challenge Partial Specifications Types Expressivity Full Functional Correctness

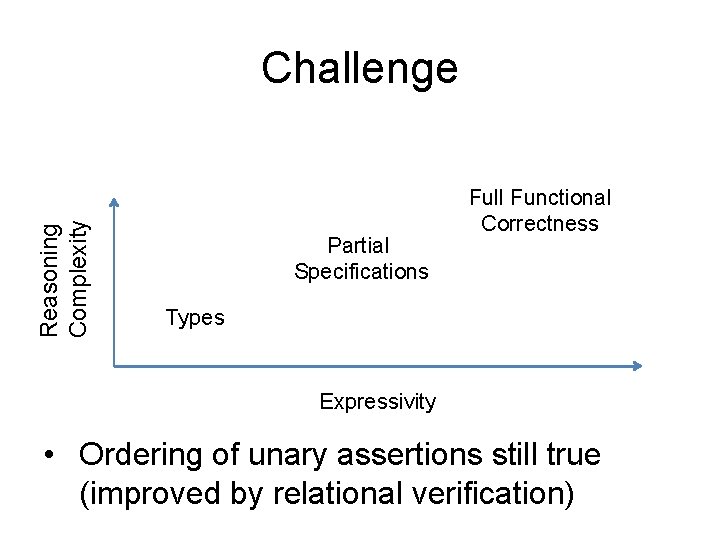
Reasoning Complexity Challenge Partial Specifications Full Functional Correctness Types Expressivity • Ordering of unary assertions still true (improved by relational verification)

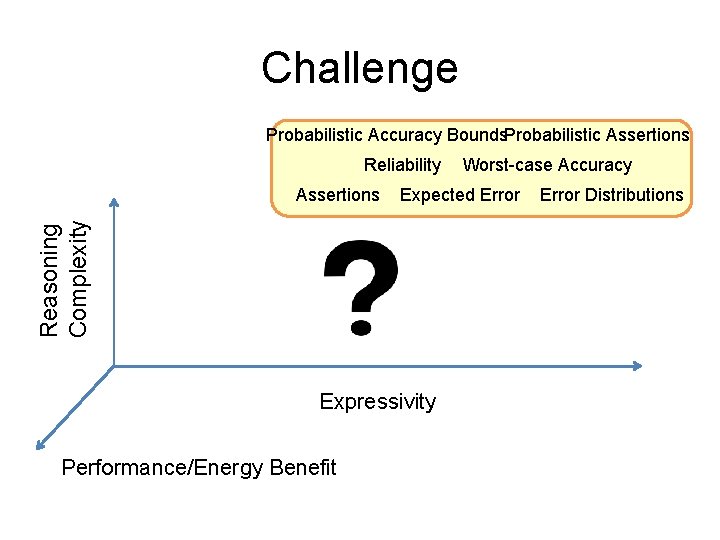
Challenge Probabilistic Accuracy Bounds. Probabilistic Assertions Reliability Worst-case Accuracy Reasoning Complexity Assertions Expected Error Expressivity Performance/Energy Benefit Error Distributions

Example: Loop Perforation (Misailovic et al. , SAS ‘ 11) float sum = 0; for (int i = 0; i < n; i += 1) { sum = sum + a[i]; i += 2 } float avg = sum / n; float avg = (sum * 2) / n;

Example: Loop Perforation (Misailovic et al. , SAS ‘ 11) float sum = 0; for (int i = 0; i < n; i += 1) { sum = sum + a[i]; i += 2 } float avg = sum / n; float avg = (sum * 2) / n; • Worst-case error: • Probabilistic Error Bound (. 95):

Question #2: “There’s no hope for building approximate hardware. ” - Unnamed Computer Architect

Challenge • Approx. PL community must work with hardware community to collaborate on models (not the PL community’s expertise) • Approx. hardware community faces major challenge in publishing deep architectural changes: simulation widely panned • Moving forward may require large joint effort

Question #3: “I believe your techniques are fundamentally flawed. ” - Unnamed Numerical Analyst

Challenge • Numerical analysts have been wronged • Programming systems have failed to provide support for making the statements they desire • Approximate computing community risks repeating work done by numerical analysis • Opportunity for collaboration • New research opportunities • It’s no longer just about floating-point

Broadly Accessible Motivations • Programming with uncertainty (uncertain operations and data) • Programming unrealizable computation (large scale numerical simulations) • Useful computation from non-digital fabrics (analog, quantum, biological, and human) Opportunity to build reliable and resilient computing systems built upon anything

End

Conclusion • Adoption hinges on tradeoff between expressivity, complexity and benefit • Opportunity/necessity for tighter integration of PL and hardware communities

Open Challenges and Directions Reasoning Complexity Probabilistic Accuracy Bounds Worst-case Accuracy Probabilistic Assertions Reliability Expected Accuracy Error Distributions Expressivity Problem: benefits (performance/energy) may vary between different types of guarantees

Open Challenges and Directions Expressivity and Reasoning Complexity Type Checking Partial Specifications Full Functional Correctness

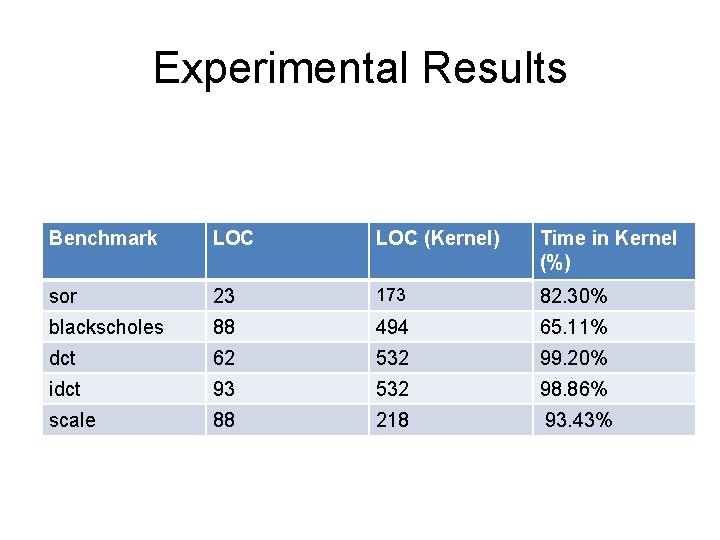
Experimental Results Benchmark LOC (Kernel) Time in Kernel (%) sor 23 173 82. 30% blackscholes 88 494 65. 11% dct 62 532 99. 20% idct 93 532 98. 86% scale 88 218 93. 43%

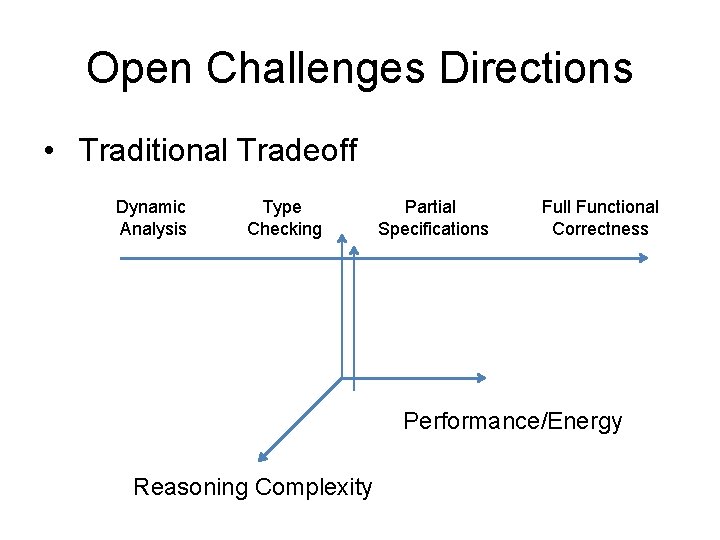
Open Challenges Directions • Traditional Tradeoff Dynamic Analysis Type Checking Partial Specifications Full Functional Correctness Performance/Energy Reasoning Complexity