Programmierkurs Java Teil Imperative Programmierung Unterrichtseinheit 16 Rekursion

Programmierkurs Java Teil Imperative Programmierung Unterrichtseinheit 16 Rekursion Dr. Dietrich Boles Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 1

Gliederung Ø Rekursion Ø Definitionen Ø Rekursive Prozeduren Ø Rekursive Funktionen Ø Lokale Variablen Ø Parameter Ø Endlosrekursion Ø Anmerkungen Ø Beispiele Ø Backtracking Ø Zusammenfassung Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 2

Rekursion (1) Ø "Definition eines Problems, einer Funktion oder eines Verfahrens durch sich selbst" Ø bereits bekannt: Ø direkt rekursive Syntaxdiagramme/EBNF: <boolescher Ausdruck> : : "true" | "false" | "(" <boolscher Ausdruck> ")" ; Ø indirekt rekursive Syntaxdiagramme/EBNF: <Anweisung> : : =. . . | <while-Anweisung> ; <while-Anweisung> : : = "while" "(" <b. A> ")" <Anweisung> ; Ø Mathematik: n! = { 1 falls n = 0 n * (n-1)! sonst Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 3

Rekursion (2) Ø Spielzeug: Quelle: German Wikipedia Matroschka Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 4

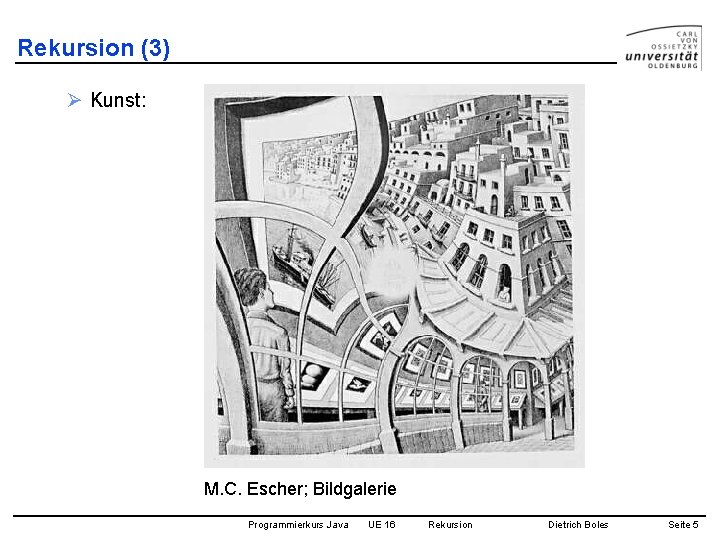
Rekursion (3) Ø Kunst: M. C. Escher; Bildgalerie Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 5

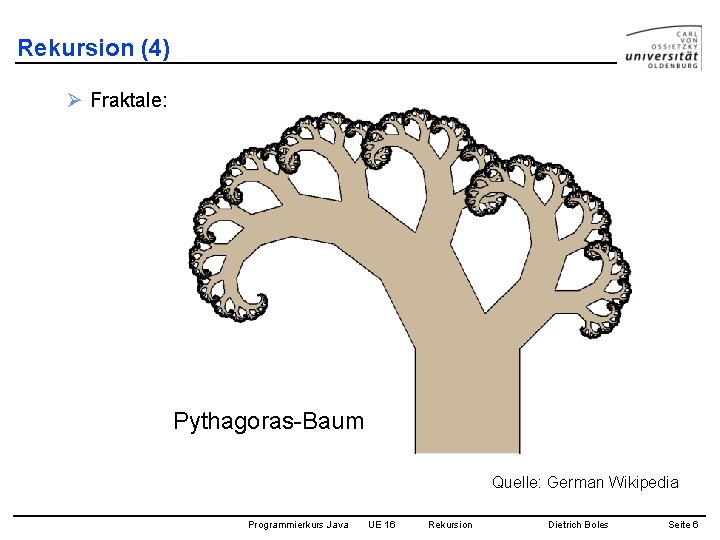
Rekursion (4) Ø Fraktale: Pythagoras-Baum Quelle: German Wikipedia Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 6

Rekursion (5) Ø Fraktale: Quelle: German Wikipedia, Wolfgag Beyer Mandelbrotmenge http: //www. mathematik. ch/anwendungenmath/fractal/julia/Mandelbrot. Applet. php Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 7

Definitionen (1) Definition (Rekursion): Eine Funktion heißt rekursiv, wenn sie während ihrer Abarbeitung erneut aufgerufen wird. Definition (direkte Rekursion): Eine Funktion heißt direkt rekursiv, wenn der erneute Aufruf im Funktionsrumpf der Funktion erfolgt. Definition (indirekte Rekursion): Eine Funktion heißt indirekt rekursiv, wenn der erneute Aufruf nicht im Funktionsrumpf der Funktion selbst sondern in einer anderen Funktion erfolgt. Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 8

Definitionen (2) Definition (Funktionsinkarnation): konkreter Aufruf einer Funktion Definition (Rekursionstiefe): Anzahl der aktuellen Inkarnationen einer Funktion minus 1 Definition (Variableninkarnation): konkrete Ausprägung (Speicherplatz) einer Variablen Iterativer Algorithmus: Algorithmus, der Wiederholungsanweisungen verwendet Rekursiver Algorithmus: Algorithmus, der rekursive Funktionen verwendet Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 9

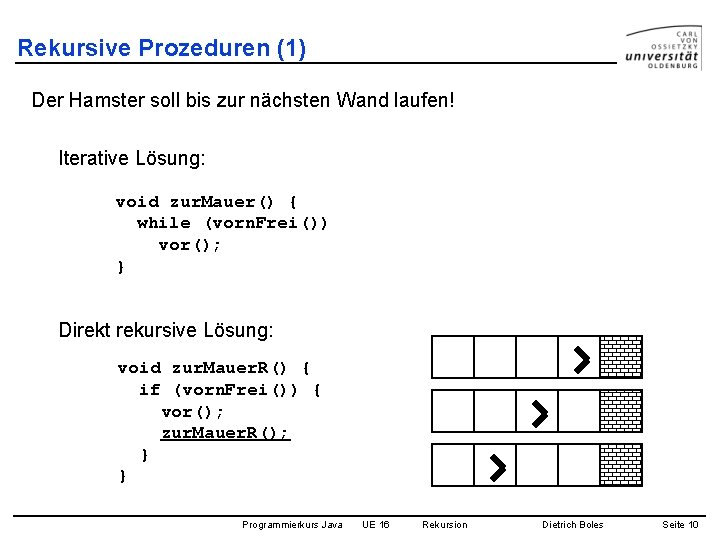
Rekursive Prozeduren (1) Der Hamster soll bis zur nächsten Wand laufen! Iterative Lösung: void zur. Mauer() { while (vorn. Frei()) vor(); } Direkt rekursive Lösung: void zur. Mauer. R() { if (vorn. Frei()) { vor(); zur. Mauer. R(); } } Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 10

Rekursive Prozeduren (2) Der Hamster soll alle Körner auf dem aktuellen Feld einsammeln! Iterative Lösung: void sammle() { while (korn. Da()) nimm(); } Direkt rekursive Lösung: void sammle. R() { if (korn. Da()) { nimm(); sammle. R(); } } Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 11

Rekursive Prozeduren (3) Der Hamster soll bis zur nächsten Wand und dann zurück zur Ausgangsposition laufen! Iterative Lösung: void hin. Und. Zurueck() { int anzahl = 0; while (vorn. Frei()) { vor(); anzahl++; } links. Um(); while (anzahl > 0) { vor(); anzahl--; } } Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 12

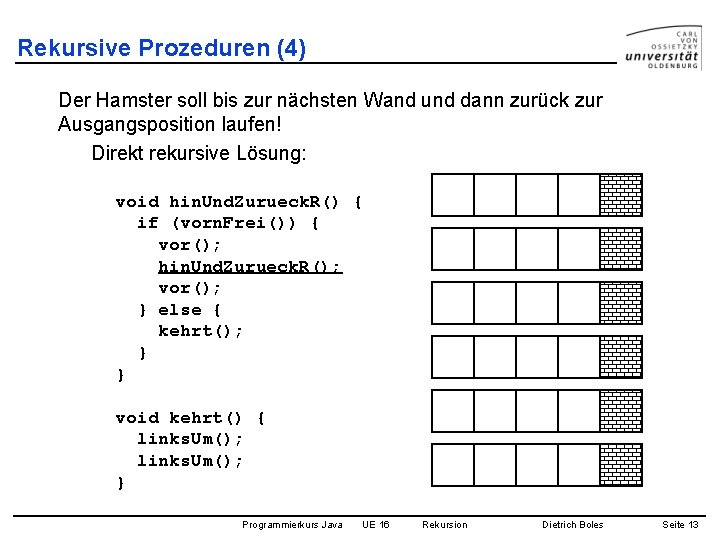
Rekursive Prozeduren (4) Der Hamster soll bis zur nächsten Wand und dann zurück zur Ausgangsposition laufen! Direkt rekursive Lösung: void hin. Und. Zurueck. R() { if (vorn. Frei()) { vor(); hin. Und. Zurueck. R(); vor(); } else { kehrt(); } } void kehrt() { links. Um(); } Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 13

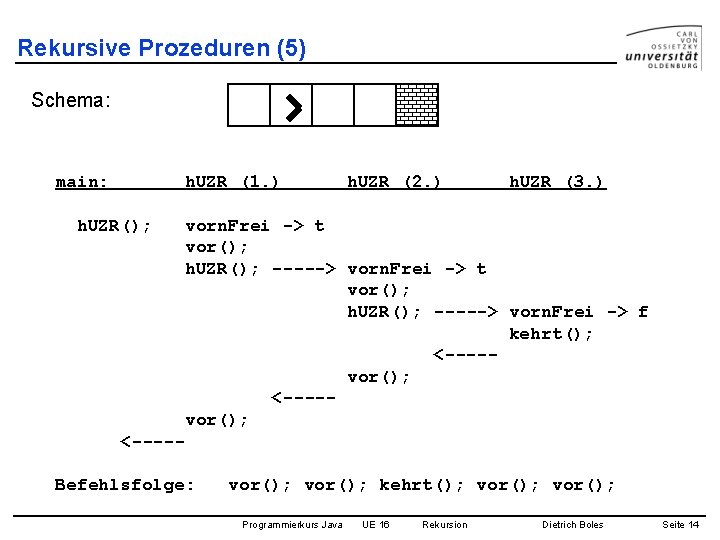
Rekursive Prozeduren (5) Schema: main: h. UZR (1. ) h. UZR(); h. UZR (2. ) h. UZR (3. ) vorn. Frei -> t vor(); h. UZR(); -----> vorn. Frei -> f kehrt(); <----vor(); <----Befehlsfolge: vor(); kehrt(); vor(); Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 14

Rekursive Prozeduren (6) Der Hamster soll bis zur nächsten Wand und dann zurück zur Ausgangsposition laufen! Indirekt rekursive Lösung: void hin. Und. Zurueck. R() { if (vorn. Frei()) { laufe(); } else { links. Um(); } } void laufe() { vor(); hin. Und. Zurueck. R(); vor(); } Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 15

Rekursive Funktionen (1) Der Hamster soll die Anzahl an Schritten bis zur nächsten Mauer zählen! Iterative Lösung: int anzahl. Schritte() { int anzahl = 0; while (vorn. Frei()) { vor(); anzahl++; } return anzahl; } Rekursive Lösung: int anzahl. Schritte. R() { if (vorn. Frei()) { vor(); return anzahl. Schritte. R() + 1; } else return 0; } Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 16

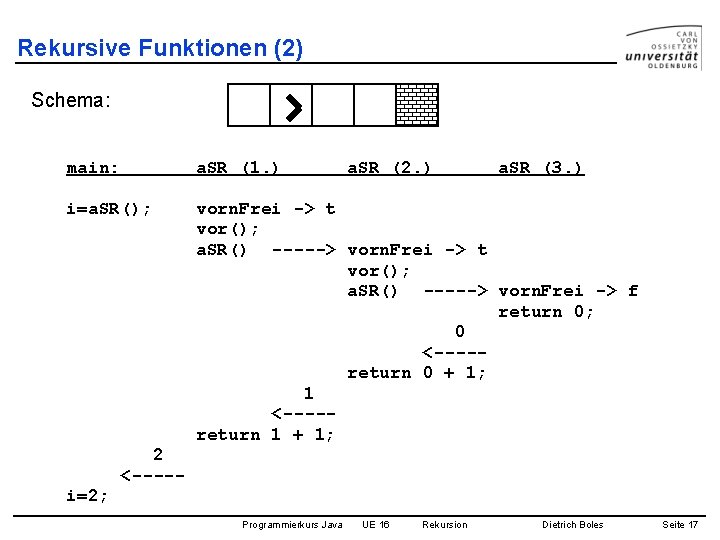
Rekursive Funktionen (2) Schema: main: a. SR (1. ) a. SR (2. ) a. SR (3. ) i=a. SR(); vorn. Frei -> t vor(); a. SR() -----> vorn. Frei -> f return 0; 0 <----return 0 + 1; 1 <----return 1 + 1; 2 <----i=2; Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 17

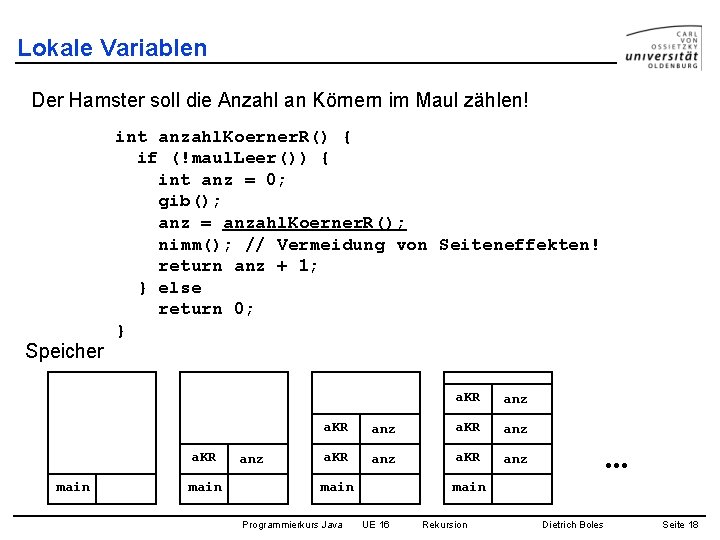
Lokale Variablen Der Hamster soll die Anzahl an Körnern im Maul zählen! Speicher int anzahl. Koerner. R() { if (!maul. Leer()) { int anz = 0; gib(); anz = anzahl. Koerner. R(); nimm(); // Vermeidung von Seiteneffekten! return anz + 1; } else return 0; } a. KR main anz a. KR anz main Programmierkurs Java . . . main UE 16 Rekursion Dietrich Boles Seite 18

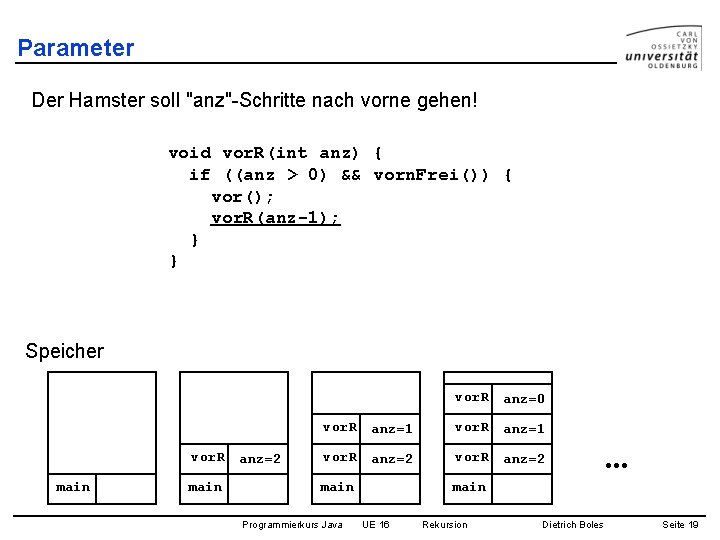
Parameter Der Hamster soll "anz"-Schritte nach vorne gehen! void vor. R(int anz) { if ((anz > 0) && vorn. Frei()) { vor(); vor. R(anz-1); } } Speicher vor. R main anz=2 vor. R anz=0 vor. R anz=1 vor. R anz=2 main Programmierkurs Java . . . main UE 16 Rekursion Dietrich Boles Seite 19

Endlosrekursion: void sammle. R() { if (korn. Da()) { sammle. R(); nimm(); } } Rekursionstiefe: im Prinzip "unendlich"! erzeugt im allgemeinen Laufzeitfehler: Stack overflow! Dem Java-Interpreter kann man die gewünschte Stackgröße mitteilen! Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 20

Anmerkungen Ø Satz: Ø zu jedem rekursiv formulierten Algorithmus gibt es einen äquivalenten iterativen Algorithmus Ø Vorteile rekursiver Algorithmen: Ø Ø kürzere Formulierung leichter verständliche Lösung Einsparung von Variablen teilweise sehr effiziente Problemlösungen (z. B. Quicksort) Ø Nachteile rekursiver Algorithmen: Ø weniger effizientes Laufzeitverhalten (Overhead beim Funktionsaufruf) Ø Verständnisprobleme bei Programmieranfängern Ø Konstruktion rekursiver Algorithmen "gewöhnungsbedürftig" Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 21

Beispiel 1 Anzahl an Ziffern einer Zahl ermitteln: static int length(int zahl) { if (zahl == 0) return 1; int laenge = 0; while (zahl != 0) { zahl /= 10; laenge++; } return laenge; } // iterativ static int length. R(int zahl) { // rekursiv if (zahl >= -9 && zahl <= 9) return 1; return length. R(zahl/10) + 1; } Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 22

Beispiel 2 Berechnung der Fakultätsfunktion: n! = { 1 falls n = 0 n * (n-1)! sonst static int fak(int n) { if (n <= 0) return 1; else return n * fak(n-1); } fak(3) = 3 * fak(2) 2 * fak(1) 1 * fak(0) 1 1 * 1 2 * 1 3 * 2 6 Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 23

Beispiel 3 Berechnung einer Fibonacci-Zahl: { fib(n) = 1 falls n = 1 1 falls n = 2 fib(n-1) + fib(n-2) sonst static int if (n <= return else return } fib(int n) { 2) 1; fib(n-1) + fib(n-2); Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 24

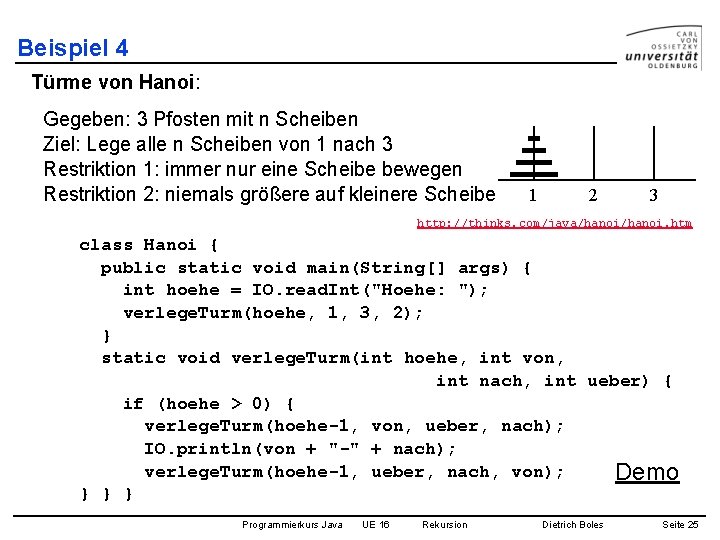
Beispiel 4 Türme von Hanoi: Gegeben: 3 Pfosten mit n Scheiben Ziel: Lege alle n Scheiben von 1 nach 3 Restriktion 1: immer nur eine Scheibe bewegen Restriktion 2: niemals größere auf kleinere Scheibe 1 2 3 http: //thinks. com/java/hanoi. htm class Hanoi { public static void main(String[] args) { int hoehe = IO. read. Int("Hoehe: "); verlege. Turm(hoehe, 1, 3, 2); } static void verlege. Turm(int hoehe, int von, int nach, int ueber) { if (hoehe > 0) { verlege. Turm(hoehe-1, von, ueber, nach); IO. println(von + "-" + nach); verlege. Turm(hoehe-1, ueber, nach, von); Demo } } } Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 25

Backtracking-Verfahren (1) Ø Prinzip: Ø Versuch, eine Teillösung eines gegebenen Problems systematisch zu einer Gesamtlösung auszubauen Ø falls in einer gewissen Situation ein weiterer Ausbau einer vorliegenden Teillösung nicht mehr möglich ist ("Sackgasse"), werden eine oder mehrere der letzten Teilschritte rückgängig gemacht Ø die dann erhaltene reduzierte Teillösung versucht man auf einem anderen Weg wieder auszubauen Ø Wiederholung des Verfahrens, bis Lösung gefunden wird oder man erkennt, dass keine Lösung existiert Ø Grundlage der Programmiersprache PROLOG! Ø Bekannte Probleme: Ø Springerproblem Ø Acht-Damenproblem Ø Labyrinthsuche Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 26

Backtracking-Verfahren (2) Aufgabe: Der Hamster steht am Eingang eines zyklenfreien Labyrinths, in dem er ein Korn finden und auf dem schnellsten Weg zurücktransportieren soll! Demo Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 27

Backtracking-Verfahren (3) void main() { durchsuche. Labyrinth(); } boolean durchsuche. Labyrinth() { if (korn. Da()) { nimm(); kehrt(); // mach dich auf den Heimweg return true; } if (links. Frei() && durchsuche. Teil. Labyrinth. Links()) { kehrt(); // mach dich auf den Heimweg return true; } if (rechts. Frei() && durchsuche. Teil. Labyrinth. Rechts()) { kehrt(); // mach dich auf den Heimweg return true; } Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 28

Backtracking-Verfahren (4) if (!vorn. Frei()) { kehrt(); // Sackgasse return false; } return durchsuche. Teil. Labyrinth. Vorne(); } boolean durchsuche. Teil. Labyrinth. Links() { links. Um(); vor(); boolean gefunden = durchsuche. Labyrinth(); // Ausgangsposition einnehmen vor(); links. Um(); return gefunden; } Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 29

Backtracking-Verfahren (5) boolean durchsuche. Teil. Labyrinth. Rechts() { rechts. Um(); vor(); boolean gefunden = durchsuche. Labyrinth(); // Ausgangsposition einnehmen vor(); rechts. Um(); return gefunden; } boolean durchsuche. Teil. Labyrinth. Vorne() { vor(); boolean gefunden = durchsuche. Labyrinth(); vor(); // Seiteneffekt: Hamster schaut in andere Richtung return gefunden; } // + Hilfsfunktionen Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 30

Zusammenfassung Ø Rekursive Funktionen: Funktionen, die während ihrer Abarbeitung erneut aufgerufen werden Ø Backtracking-Verfahren: Problemlösungsverfahren, das rekursiv Teilwege durchforstet, um eine Lösung zu finden Programmierkurs Java UE 16 Rekursion Dietrich Boles Seite 31