PROGRAMME F 10 FUNCTIONS STROUD Worked examples and

PROGRAMME F 10 FUNCTIONS STROUD Worked examples and exercises are in the text

Programme F 10: Functions Processing numbers Composition – ‘function of a function’ Trigonometric functions Exponential and logarithmic functions Odd and even functions STROUD Worked examples and exercises are in the text

Programme F 10: Functions Processing numbers Composition – ‘function of a function’ Trigonometric functions Exponential and logarithmic functions Odd and even functions STROUD Worked examples and exercises are in the text

Programme F 10: Functions Processing numbers Functions are rules but not all rules are functions Functions and the arithmetic operations Inverses of functions Graphs of inverses The graph of y = x 3 The graph of y = x 1/3 The graphs of y = x 3 and y = x 1/3 plotted together STROUD Worked examples and exercises are in the text

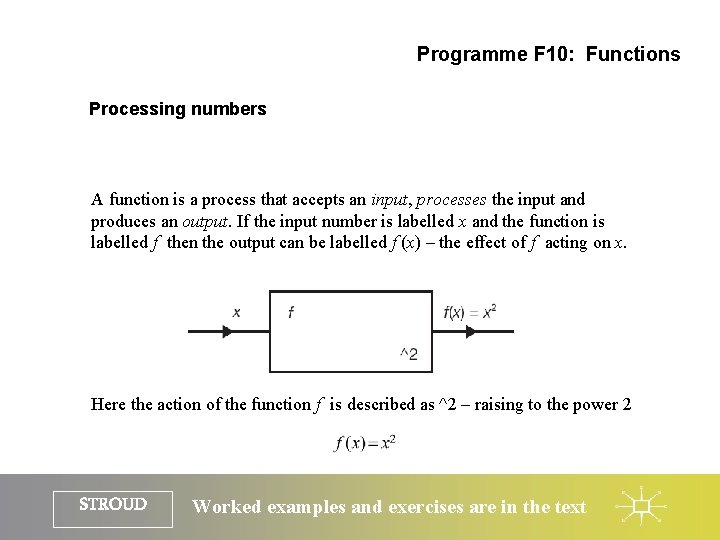
Programme F 10: Functions Processing numbers A function is a process that accepts an input, processes the input and produces an output. If the input number is labelled x and the function is labelled f then the output can be labelled f (x) – the effect of f acting on x. Here the action of the function f is described as ^2 – raising to the power 2 STROUD Worked examples and exercises are in the text

Programme F 10: Functions Processing numbers Functions are rules but not all rules are functions A function of a variable x is a rule that describes how a value of the variable is manipulated to generate a value of the variable y. The rule is often expressed in the form of an equation y = f (x) with the proviso that for any single input x there is just one output y – the function is said to be single valued. Different outputs are associated with different inputs. Other rules may not be single valued, for example: This rule is not a function. STROUD Worked examples and exercises are in the text

Programme F 10: Functions Processing numbers Functions are rules but not all rules are functions All the input numbers x that a function can process are collectively called the function’s domain. The complete collection of numbers y that correspond to the numbers in the domain is called the range (or co-domain) of the function. STROUD Worked examples and exercises are in the text

Programme F 10: Functions Processing numbers Functions and the arithmetic operations Functions can be combined under the action of the arithmetic operators provided care is taken over their common domains. STROUD Worked examples and exercises are in the text

Programme F 10: Functions Processing numbers Inverses of functions The process of generating the output of a function from the input is assumed to be reversible so that what has been constructed can be de-constructed. The rule that describes the reverse process is called the inverse of the function which is labelled: STROUD Worked examples and exercises are in the text

Programme F 10: Functions Processing numbers Graphs of inverses The ordered pairs of input-output numbers that are used to generate the graph of a function are reversed for the inverse function. Consequently, the graph of the inverse of a function is the shape of the graph of the original function reflected in the line f (x) = x. STROUD Worked examples and exercises are in the text

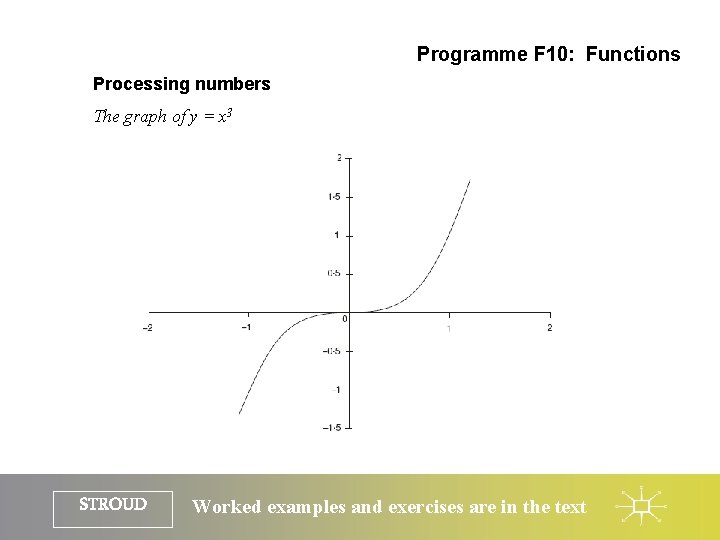
Programme F 10: Functions Processing numbers The graph of y = x 3 STROUD Worked examples and exercises are in the text

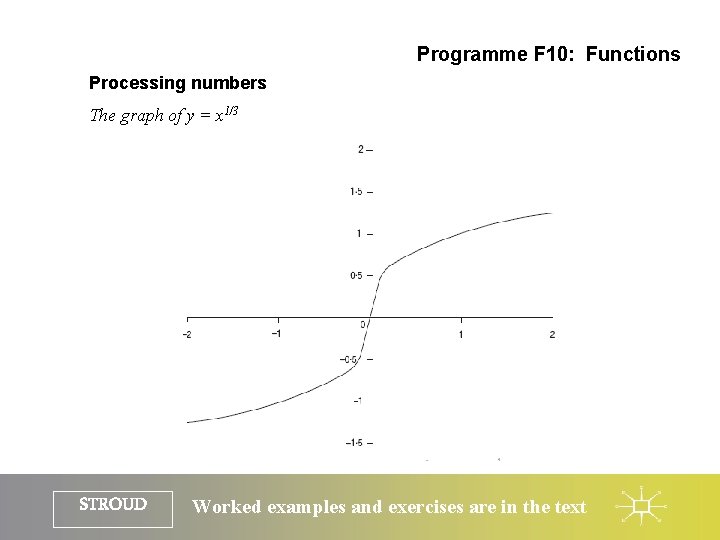
Programme F 10: Functions Processing numbers The graph of y = x 1/3 STROUD Worked examples and exercises are in the text

Programme F 10: Functions Processing numbers The graphs of y = x 3 and y = x 1/3 plotted together STROUD Worked examples and exercises are in the text

Programme F 10: Functions Processing numbers Composition – ‘function of a function’ Trigonometric functions Exponential and logarithmic functions Odd and even functions STROUD Worked examples and exercises are in the text

Programme F 10: Functions Composition – ‘function of a function’ Chains of functions can by built up where the output from one function forms the input to the next function in the chain. For example: The function f is composed of the two functions a and b where: STROUD Worked examples and exercises are in the text

Programme F 10: Functions Composition – ‘function of a function’ Inverses of compositions The diagram of the inverse can be drawn with the information flowing in the opposite direction. STROUD Worked examples and exercises are in the text

Programme F 10: Functions Composition – ‘function of a function’ Inverses of compositions STROUD Worked examples and exercises are in the text

Programme F 10: Functions Processing numbers Composition – ‘function of a function’ Trigonometric functions Exponential and logarithmic functions Odd and even functions STROUD Worked examples and exercises are in the text

Programme F 10: Functions Trigonometric functions Rotation The tangent Period Amplitude Phase difference Inverse trigonometric functions Trigonometric equations Equations of the form acos x + bsin x = c STROUD Worked examples and exercises are in the text

Programme F 10: Functions Trigonometric functions Rotation For angles greater than zero and less than /2 radians the trigonometric ratios are well defined and can be related to the rotation of the radius of a unit circle: STROUD Worked examples and exercises are in the text

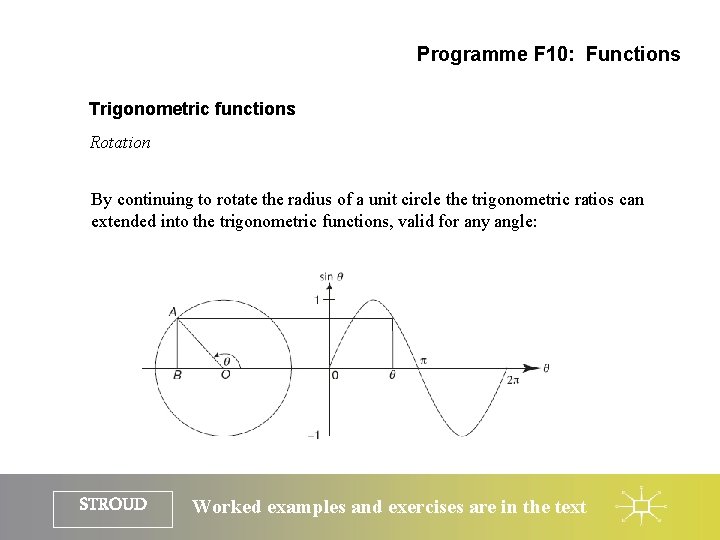
Programme F 10: Functions Trigonometric functions Rotation By continuing to rotate the radius of a unit circle the trigonometric ratios can extended into the trigonometric functions, valid for any angle: STROUD Worked examples and exercises are in the text

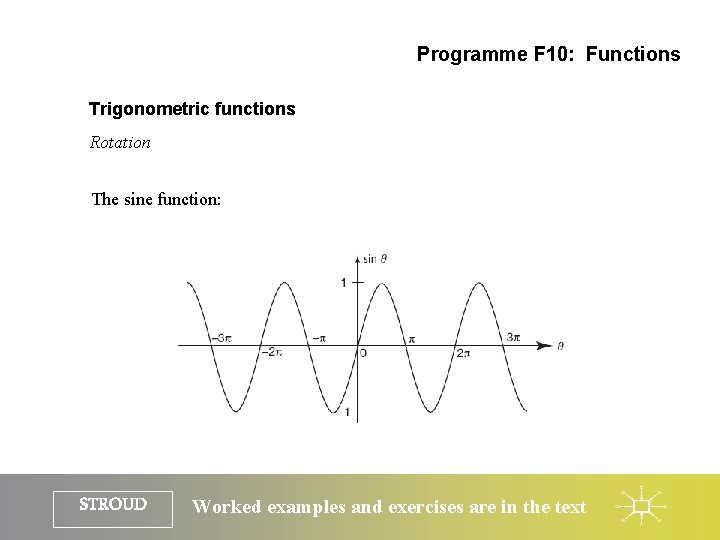
Programme F 10: Functions Trigonometric functions Rotation The sine function: STROUD Worked examples and exercises are in the text

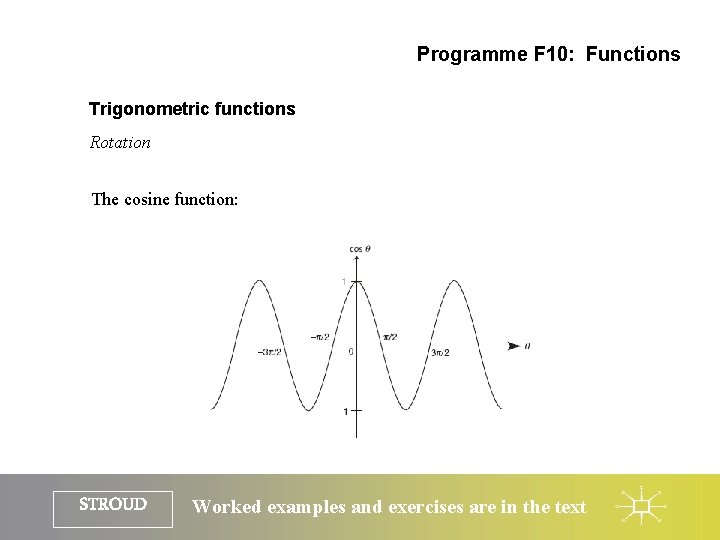
Programme F 10: Functions Trigonometric functions Rotation The cosine function: STROUD Worked examples and exercises are in the text

Programme F 10: Functions Trigonometric functions The tangent is the ratio of the sine to the cosine: STROUD Worked examples and exercises are in the text

Programme F 10: Functions Trigonometric functions Period Any function whose output repeats itself over a regular interval is called a periodic function, the regular interval being called the period of the function. The sine and cosine functions are periodic with period 2. The tangent function is periodic with period . STROUD Worked examples and exercises are in the text

Programme F 10: Functions Trigonometric functions Amplitude Every periodic function possesses an amplitude that is given as the difference between the maximum value and the average value of the output taken over a single period. STROUD Worked examples and exercises are in the text

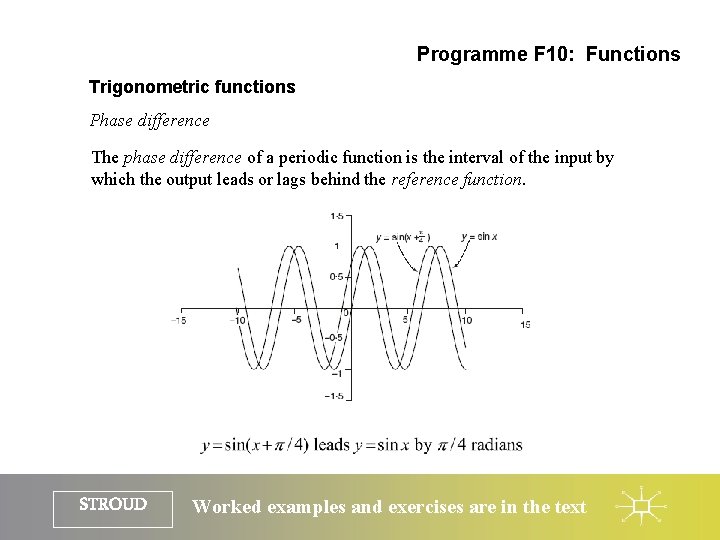
Programme F 10: Functions Trigonometric functions Phase difference The phase difference of a periodic function is the interval of the input by which the output leads or lags behind the reference function. STROUD Worked examples and exercises are in the text

Programme F 10: Functions Trigonometric functions Inverse trigonometric functions If the graph of y = sin x is reflected in the line y = x a function does not result. STROUD Worked examples and exercises are in the text

Programme F 10: Functions Trigonometric functions Inverse trigonometric functions Cutting off the upper and lower parts of the graph produces a single-valued function that is the inverse sine function. STROUD Worked examples and exercises are in the text

Programme F 10: Functions Trigonometric functions Inverse trigonometric functions Similarly for the inverse cosine function and the inverse tangent function. STROUD Worked examples and exercises are in the text

Programme F 10: Functions Trigonometric functions Trigonometric equations A simple trigonometric equation is one that involves just a single trigonometric expression: For example: STROUD Worked examples and exercises are in the text

Programme F 10: Functions Trigonometric functions Trigonometric equations As another example: STROUD Worked examples and exercises are in the text

Programme F 10: Functions Trigonometric functions Equations of the form acos x + bsin x = c The equation acos x + bsin x = c can be rewritten as: Remembering that multiple solutions can be found by using the graph. STROUD Worked examples and exercises are in the text

Programme F 10: Functions Processing numbers Composition – ‘function of a function’ Trigonometric functions Exponential and logarithmic functions Odd and even functions STROUD Worked examples and exercises are in the text

Programme F 10: Functions Exponential and logarithmic functions Exponential functions Indicial equations STROUD Worked examples and exercises are in the text

Programme F 10: Functions Exponential and logarithmic functions Exponential functions The exponential function is expressed by the equation: Where e is the exponential number 2. 7182818. . . The value of ex can be found to any level of precision desired from the series expansion: STROUD Worked examples and exercises are in the text

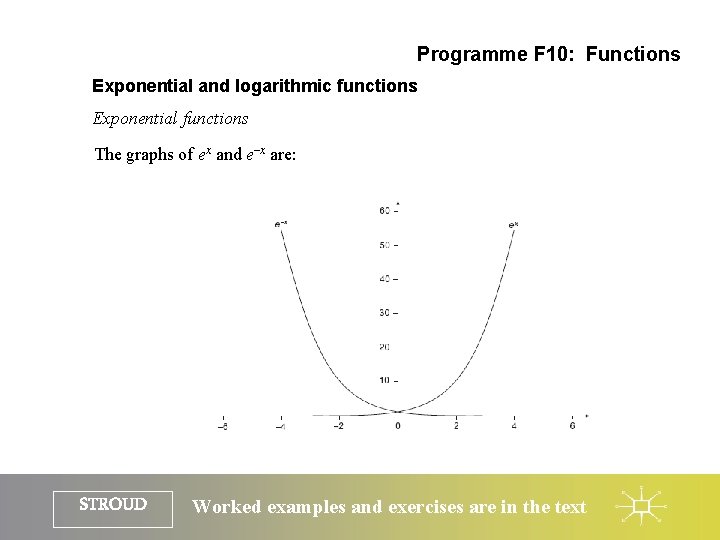
Programme F 10: Functions Exponential and logarithmic functions Exponential functions The graphs of ex and e–x are: STROUD Worked examples and exercises are in the text

Programme F 10: Functions Exponential and logarithmic functions Exponential functions The general exponential function is given by y = ax where a > 0. Since a = elna the general exponential function can be written as: STROUD Worked examples and exercises are in the text

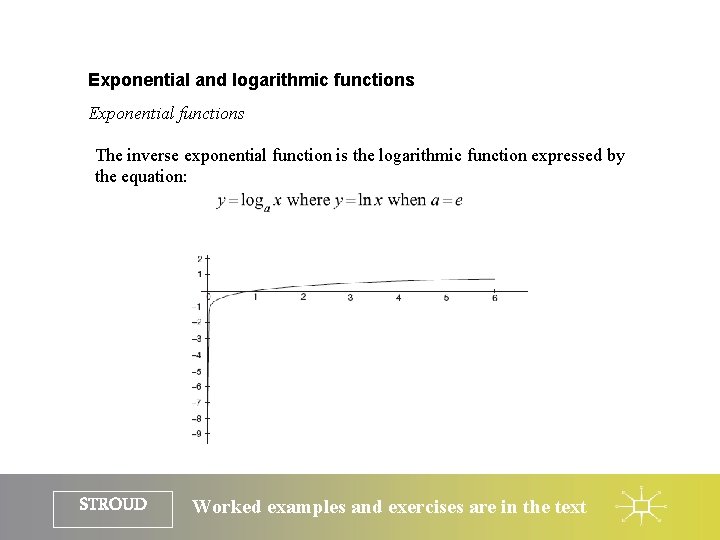
Exponential and logarithmic functions Exponential functions The inverse exponential function is the logarithmic function expressed by the equation: STROUD Worked examples and exercises are in the text

Programme F 10: Functions Exponential and logarithmic functions Indicial equations An indicial equation is an equation where the variable appears as an index and the solution of such equations requires application of logarithms. STROUD Worked examples and exercises are in the text

Programme F 10: Functions Processing numbers Composition – ‘function of a function’ Trigonometric functions Exponential and logarithmic functions Odd and even functions STROUD Worked examples and exercises are in the text

Programme F 10: Functions Odd and even functions Odd and even parts of the exponential function Limits of functions The rules of limits STROUD Worked examples and exercises are in the text

Programme F 10: Functions Odd and even functions Given a function f with output f (x) then, assuming f (−x) is defined: If f (−x) = f (x) the function f is called an even function If f (−x) = f (x) the function f is called an odd function STROUD Worked examples and exercises are in the text

Programme F 10: Functions Odd and even functions Odd and even parts If, given f (x) where f (−x) is defined then: STROUD Worked examples and exercises are in the text

Programme F 10: Functions Odd and even functions Odd and even parts of the exponential function The even part of the exponential function is: The odd part of the exponential function is: Notice: STROUD Worked examples and exercises are in the text

Programme F 10: Functions Odd and even functions Limits of functions There are times when a function has no defined output for a particular value of x, say x 0, but that it does have a defined value for values of x arbitrarily close to x 0. For example: However, so when x is close to 1 f (x) is close to 2. it is said that: the limit of f (x) as x approaches the value x = 1 is 2 STROUD Worked examples and exercises are in the text

Programme F 10: Functions Odd and even functions Limits of functions The limit of f (x) as x approaches the value x = 1 is 2. Symbolically this is written as: STROUD Worked examples and exercises are in the text

Programme F 10: Functions Odd and even functions The rules of limits STROUD Worked examples and exercises are in the text

Programme F 10: Functions Odd and even functions The rules of limits STROUD Worked examples and exercises are in the text

Programme F 10: Functions Learning outcomes üIdentify a function as a rule and recognize rules that are not functions üDetermine the domain and range of a function üConstruct the inverse of a function and draw its graph üConstruct compositions of functions and de-construct them into their components üDevelop the trigonometric functions from the trigonometric ratios üFind the period, amplitude and phase of a periodic function More. . . STROUD Worked examples and exercises are in the text

Programme F 10: Functions Learning outcomes üDistinguish between the inverse of a trigonometric function and the inverse trigonometric function ü Solve trigonometric equations using the inverse trigonometric functions üRecognize that the exponential and natural logarithmic functions are mutual inverses and solve indicial and logarithmic equations üConstruct the hyperbolic functions from the odd and even parts of the exponential function üEvaluate limits of simple functions STROUD Worked examples and exercises are in the text