Programme 23 Polar coordinate systems PROGRAMME 23 POLAR

Programme 23: Polar coordinate systems PROGRAMME 23 POLAR COORDINATE SYSTEMS STROUD Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Introduction to polar coordinates Polar curves Standard polar curves Applications STROUD Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Introduction to polar coordinates Polar curves Standard polar curves Applications STROUD Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Introduction to polar coordinates The position of a point in a plane can be represented by: (a) Cartesian coordinates (x, y) (b) polar coordinates (r, θ) The two systems are related by the equations: STROUD Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Introduction to polar coordinates Given that: then: STROUD Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Introduction to polar coordinates Polar curves Standard polar curves Applications STROUD Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Introduction to polar coordinates Polar curves Standard polar curves Applications STROUD Worked examples and exercises are in the text

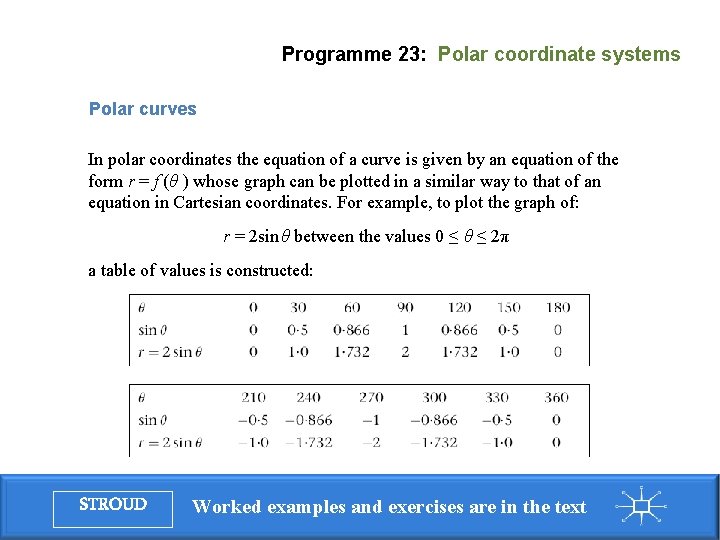
Programme 23: Polar coordinate systems Polar curves In polar coordinates the equation of a curve is given by an equation of the form r = f (θ ) whose graph can be plotted in a similar way to that of an equation in Cartesian coordinates. For example, to plot the graph of: r = 2 sin θ between the values 0 ≤ θ ≤ 2π a table of values is constructed: STROUD Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Polar curves From the table of values it is then a simple matter to construct the graph of: r = 2 sin θ (a) Choose a linear scale for r and indicate it along the initial line. (b) The value for r is then laid off along each direction in turn, point plotted, and finally joined up with a smooth curve. STROUD Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Polar curves Note: When dealing with the 210º direction, the value of r obtained is negative and this distance is, therefore, laid off in the reverse direction which brings the plot to the 30º direction. For values of θ between 180º and 360º the value obtained for r is negative and the first circle is retraced exactly. The graph, therefore, looks like one circle but consists of two circles one on top of the other. STROUD Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Polar curves As a further example the plot of: r = 2 sin 2θ exhibits the two circles distinctly. STROUD Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Introduction to polar coordinates Polar curves Standard polar curves Applications STROUD Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Introduction to polar coordinates Polar curves Standard polar curves Applications STROUD Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Standard polar curves r = a sin θ STROUD r = a sin 2θ Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Standard polar curves r = a cos θ STROUD r = a cos 2θ Worked examples and exercises are in the text

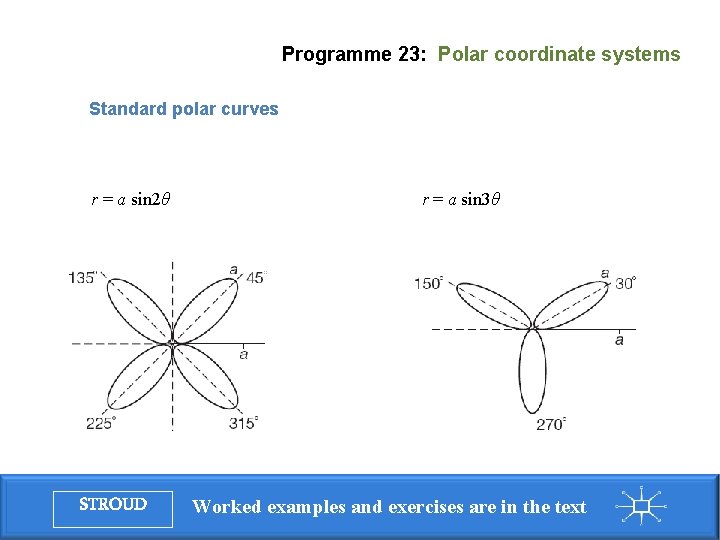
Programme 23: Polar coordinate systems Standard polar curves r = a sin 2θ STROUD r = a sin 3θ Worked examples and exercises are in the text

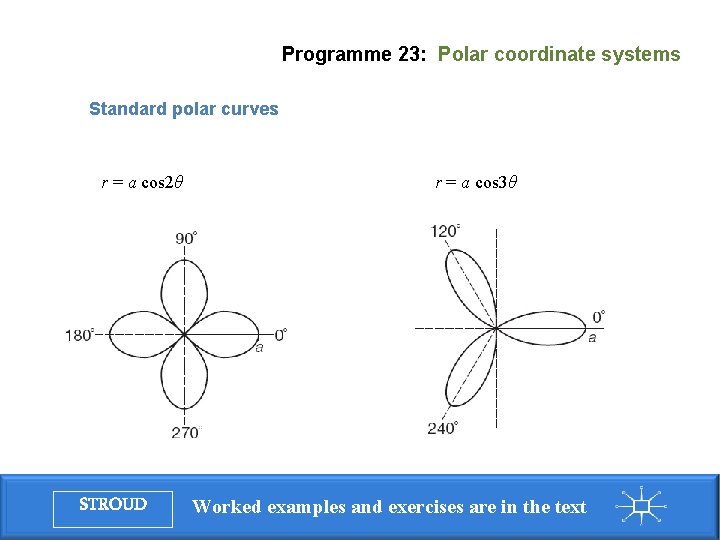
Programme 23: Polar coordinate systems Standard polar curves r = a cos 2θ STROUD r = a cos 3θ Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Standard polar curves r = a(1 + cosθ ) STROUD r = a(1 + 2 cosθ ) Worked examples and exercises are in the text

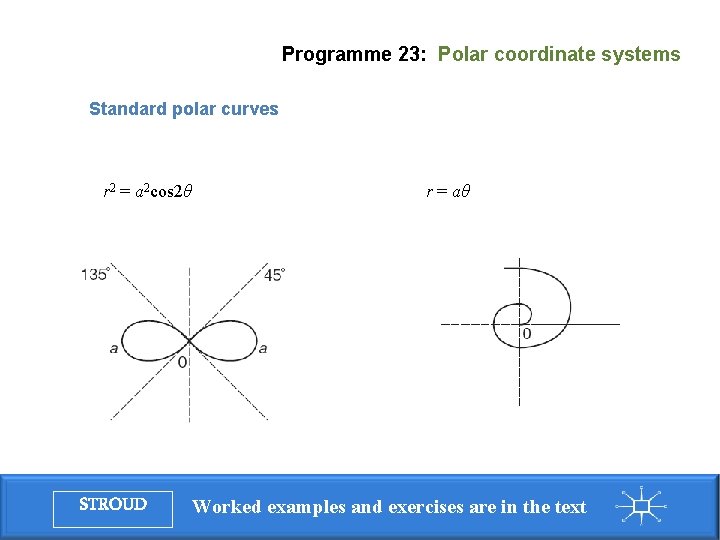
Programme 23: Polar coordinate systems Standard polar curves r 2 = a 2 cos 2θ STROUD r = aθ Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Standard polar curves The graphs of r = a + b cos θ STROUD Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Introduction to polar coordinates Polar curves Standard polar curves Applications STROUD Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Introduction to polar coordinates Polar curves Standard polar curves Applications STROUD Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Applications Area of a plane figure bounded by a polar curve Volume of rotation of a polar curve Arc length of a polar curve Surface of rotation of a polar curve STROUD Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Applications Area of a plane figure bounded by a polar curve Area of sector OPQ is δA where: Therefore: STROUD Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Applications Volume of rotation of a polar curve Area of sector OPQ is δA where: The volume generated when OPQ rotates about the x-axis is δV where : STROUD Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Applications Volume of rotation of a polar curve Since: so: STROUD Worked examples and exercises are in the text

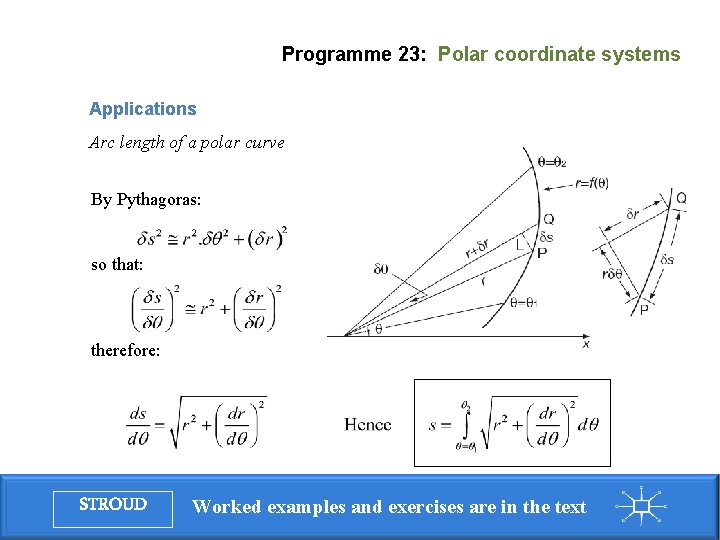
Programme 23: Polar coordinate systems Applications Arc length of a polar curve By Pythagoras: so that: therefore: STROUD Worked examples and exercises are in the text

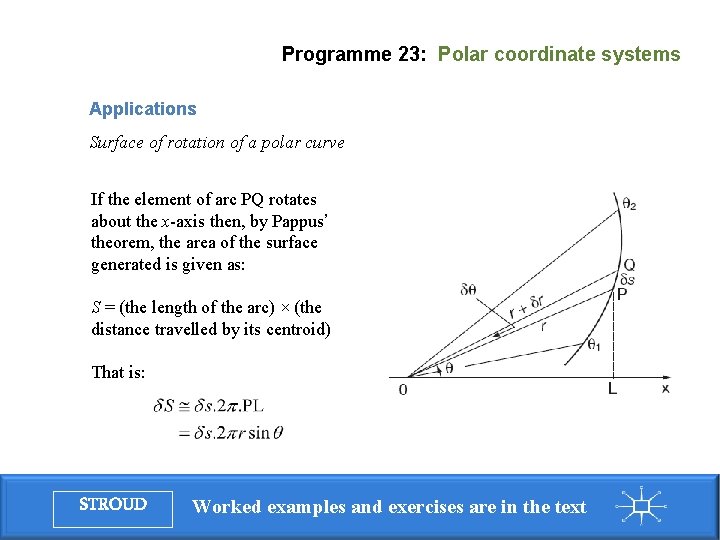
Programme 23: Polar coordinate systems Applications Surface of rotation of a polar curve If the element of arc PQ rotates about the x-axis then, by Pappus’ theorem, the area of the surface generated is given as: S = (the length of the arc) × (the distance travelled by its centroid) That is: STROUD Worked examples and exercises are in the text

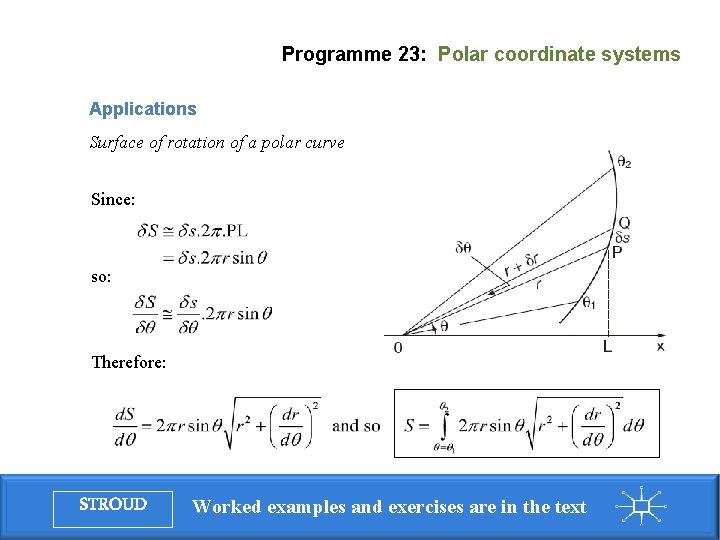
Programme 23: Polar coordinate systems Applications Surface of rotation of a polar curve Since: so: Therefore: STROUD Worked examples and exercises are in the text

Programme 23: Polar coordinate systems Learning outcomes üConvert expressions from Cartesian coordinates to polar coordinates üPlot the graphs of polar curves üRecognize equations of standard polar curves üEvaluate the areas enclosed by polar curves üEvaluate the volumes of revolution generated by polar curves üEvaluate the lengths of polar curves üEvaluate the surfaces of revolution generated by polar curves STROUD Worked examples and exercises are in the text