Programmation procdurale Transformations 1 C Transformation 2 Dfinition

Programmation procédurale Transformations 1. C. Transformation 2. Définition 3. Quelques transformations remarquables 4. Bohm et Jacoppini : B --> D 5. Méthode par automate : B --> D 6. Arsac : B --> REn 1. 2. 7. Ramshaw : B-->REn Williams and Chen : B --> D R --> B ( procédé sémantique)

Programmation procédurale Transformations � Introduction • Une transformation de programmes est une modification source à source. • Une transformation doit être compréhensible, assurer l'équivalence, précise pour permettre une automatisation. On distingue : - les transformations syntaxiques : dépendent uniquement de la forme du programme. - les transformations sémantiques : tiennent compte de la signification du programme (éliminer les test inutile, détecter et éliminer les parties inaccessibles d'un programme, . . . ) • Toutes les transformations que nous développons ici sont fonctionnelles.

Programmation procédurale Transformations � Introduction : Pourquoi transformer des algorithmes ? • Chaque type de construction représente un mode de pensée. Donc, un programmeur conçoit son algorithme à sa façon dans un formalisme de son choix. Puis, il l'exprime dans une forme structurée dans le but de le rendre plus lisible et plus facile à le mettre au point. • Domaines d'utilisation : . Synthèse des programmes (Partir d'une spécification mathématique et arriver par une série de transformations à un programme). Structuration d'algorithmes

Programmation procédurale Transformations � Introduction • Toutes les structures que nous avons présentées ( des langages procéduraux) peuvent être répartie en deux catégories : ceux qui utilisent des saut explicites ( avec goto, exit) et ceux qui utilisent des saut implicites( D, BJ, . . ). Les premières se transforment trivialement vers les B, les second de la même façon vers les D. Il est donc intéressant d'étudier le passage entre les B et les D algorithmes. Deux articles contradictoires méritent d'être évoqués : - DIJKSTRA(1968) critique l'utilisation des GOTO " L'instruction GOTO a des effets désastreux" - KNUTH (1974) "Programmation structurée avec GOTO". Le GOTO pourrait être un outil efficace s'il est bien utilisé.

Programmation procédurale Transformations � Bohm et Jaccopinni (1966)

Programmation procédurale Transformations � Technique par automate • Pour tout B-algorithme, on associe un automate et on donne son algorithme correspondant. Chaque étiquette dans le B-algorithme représente un état dans l'automate. Quelques étiquettes additionnels sont nécessaires au niveau du B-algorithme pour réaliser la transformation.

Programmation procédurale Transformations � Technique par automate • Soit le B-algorithme suivant : a b E 1 c d IF t 1 GOTO E 2 x E 3 IF t 2 GOTO E 4 z GOTO E 1 E 2 r s u GOTO E 3 u v E 4 x y z

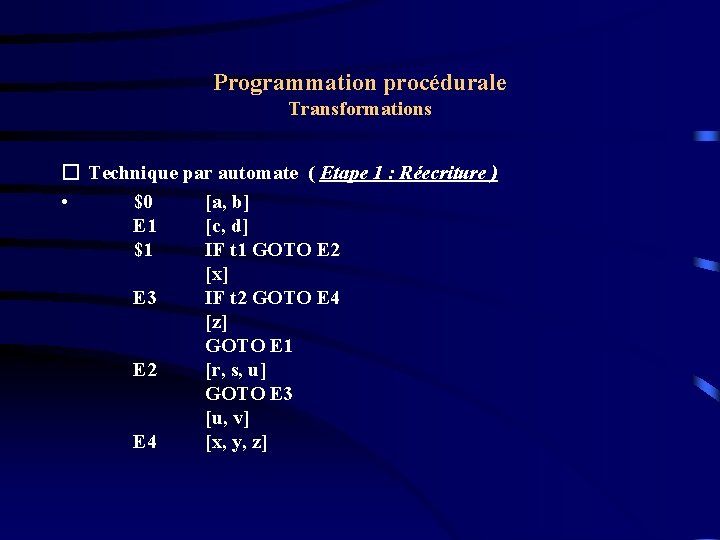
Programmation procédurale Transformations � Technique par automate ( Etape 1 : Réecriture ) • Étiqueter la première instruction. • Étiqueter aussi toute instruction conditionnel contenue dans le Balgorithme. • Si plusieurs actions atomiques se suivent et ne sont pas étiquetées, les rassembler en une séquence. • En plus, pour chaque état(Label), associer la condition correspondante par la construction d'une table de correspondance(COND) entre les états et les conditions.

Programmation procédurale Transformations � Technique par automate ( Etape 1 : Réecriture ) • $0 [a, b] E 1 [c, d] $1 IF t 1 GOTO E 2 [x] E 3 IF t 2 GOTO E 4 [z] GOTO E 1 E 2 [r, s, u] GOTO E 3 [u, v] E 4 [x, y, z]

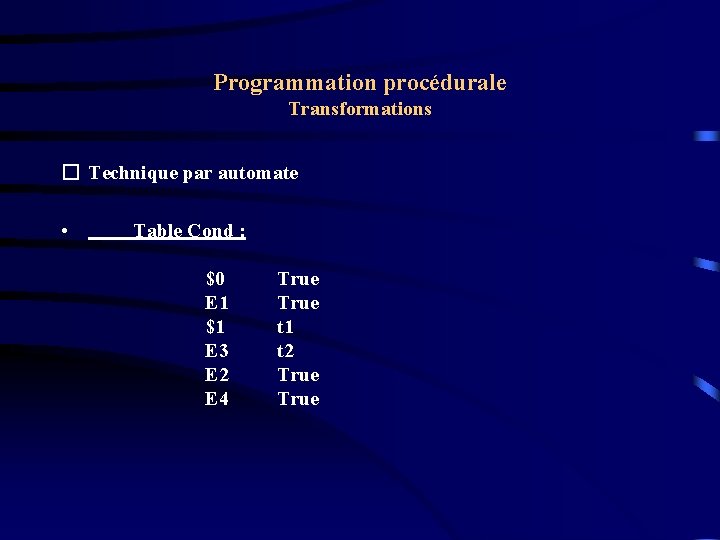
Programmation procédurale Transformations � Technique par automate • Table Cond : $0 E 1 $1 E 3 E 2 E 4 True t 1 t 2 True

Programmation procédurale Transformations 1. Technique par automate ( Etape 2 : matrice de transition ) 2. Construire la matrice de transition à partir du B-algorithme. 3. Pour chaque état S, si la condition associée(dans COND) est vrai c'est MAT(S, True) qui est considéré sinon c'est MAT(S, False). 4. Considérer veut dire l'action avant le symbole avant --> est exécutée, puis aller à l'état figurant après '->'. 5. Remarquer que la séquence [u, v] is supprimée comme elle n'est pas accessible.

Programmation procédurale Transformations � Technique par automate ( Etape 3 : D-algorithme ) • Donner le D-algorithme correspondant. • On utilise "IF THEN ELSE" en cascade. • Chaque "if statement" correspond à une ligne de la matrice. • Si un état à une valeur toujours vrai dans COND, donner simplement les actions correspondantes sil elles existent suivie par la modification de l'état courant.

Programmation procédurale Transformations 1. Technique par automate ( Etape 3 : D-algorithme ) 2. Si un état a une condition t, donner un choix entre les deux colonnes de la matrice selon la valeur logique de t. Par exemple, à la ligne E 3 de la matrice on associe l'alternative suivante : If Cond(E 3) : State : = E 4 Else z ; State : = E 1 Endif

Programmation procédurale Transformations 1. Technique par automate 2. Pour l'exemple, on obtient : (State est une variable. F désigne l'état finale ) { Initialisation } State : = $0 WHILE ( State # F ) : IF State = $0 : a; b; State : = E 1 ELSE IF State = E 1 : c; d; State : = $1 ELSE IF State = $1 : IF t 1 : State : = E 2 ELSE x; State : = E 3 ENDIF

Programmation procédurale Transformations � Technique par automate ELSE IF State = E 2 : r; s, u; State : = E 3 ELSE IF State = E 3 : IF t 2 : State : = E 4 ELSE z; State : = E 1 ENDIF ELSE IF State = E 4 : x; y; z; State : = F ENDIF ENDIF ENDWHILE

Programmation procédurale Transformations � Arsac REn-->D (1977) • La technique revient à poser le programme sous la forme d'un système de d'équations où les inconnus sont les étiquettes puis à le résoudre. • Le programme en sortie est un programme RE-n ( exit multiniveaux)

Programmation procédurale Transformations • Arsac REn-->D (1977) • Méthode : a) Etiquetter la première instruction. b) Introduire les "sinon" : c) Mise en équation : d) Résoudre le système : d 1)Substitution ( élimination d'une variable) , revient à substituer les variables non récursives. d 2) Récursifier / Dérécursifier

Programmation procédurale Transformations � Arsac REn-->D (1977) • Soit le B-algorithme suivant : a 4: IF t GOTO 5 2: b IF u GOTO 3 IF v GOTO 9 c GOTO 2 3: d GOTO 4 5: e GOTO 4 9 w

Programmation procédurale Transformations � Arsac REn-->D (1977) • a) Etiquetter la première instruction. Faire précéder toute instruction étiquetée, sauf la première, par une instruction GOTO. On obtient ainsi en écrivant les instructions en ligne, séparées par des "; " : 1 : a; GOTO 4; 4 : IF (t) GOTO 5; GOTO 2; 2 : b; IF(u) GOTO 3; IF(v) GOTO 9; c; GOTO 2; 3 : d; GOTO 4; 5 : e; GOTO 4; 9: w Comme vous pouvez le constater, les instructions étiquetées 3 et 5 ne sont pas suivies de Goto à l’étiquette suivante, car l'ajout de ces derniers rend les Goto 4 non terminaux.

Programmation procédurale Transformations � Arsac REn-->D (1977) • b) Introduire les "sinon" : 1: a; GOTO 4 4: Si non t : GOTO 2 Sinon GOTO 5 Finsi 2: b; Si non u : Si non v : c; GOTO 2 Sinon GOTO 9 Fsi Sinon GOTO 3 Finsi 3: d; GOTO 4 5: e; GOTO 4 9: w Il n'est pas nécessaire d'ordonner les lignes; Chacune d'entre elles désigne explicitement son successeur. Par contre une ligne doit être distinguée : celle par laquelle l'exécution doit commencer.

Programmation procédurale Transformations � Arsac REn-->D (1977) • Nous allons faire une nouvelle transformation, chaque ligne est considérée comme une action du programme, et nommée. De manière simple la ligne p sera appelée Xp. • L'appel d'une action par GOTO p sera abrégé en Xp, soit <--¨-un signe qui fera distinguer le nom de la première action Xp, donc on obtient : c) Mise en équation : X 1 = a; X 4 = Si non t : X 2 Sinon X 5 Fsi X 2 = b; Si non u : Si non v : c; X 2 Sinon X 9 Fsi Sinon X 3 Fsi X 3 = d; X 4 X 5 = e; X 4

Programmation procédurale Transformations � Arsac REn-->D (1977) • Le remplacement dans une action de GOTO p par la ligne numérotée p se traduit ici par le remplacement d'une variable Xp par sa définition. • Les actions sont des équations de programme définissant les variables d'actions. • Chaque variable est définie exactement une fois. • Les définitions ne sont pas ordonnées, mais l'une d'elles est distinguée (la variable résultat).

Programmation procédurale Transformations 1. Arsac REn-->D (1977) • d) Résoudre le système : Le système comporte une variable W non définie par une équation, son effet est d'occuper une place terminale, mais elle est sans action. Résoudre le système revient à trouver une équation X 1<--¨--y(W), si l'on aboutit à cette équation, il suffit de remplacer W par !0 ainsi la formule équivalente, au programme cherché, sera : X 1<--y(!0).

Programmation procédurale Transformations � Arsac REn-->D (1977) • d 1)Substitution ( élimination d'une variable) : On ne peut éliminer ainsi la variable X 1, qui est celle qu'on cherche à "calculer". La variable W ne doit pas être substituée non plus jusqu'à ce qu'il n'en reste aucune variable à éliminer. Le processus peut être répété tant que le système comporte des variables autre que X 1 ou W, non récursives.

Programmation procédurale Transformations � Arsac REn-->D (1977) • Substituer les variables non récursives. En appliquant ceci à l'exemple on aura après remplacement de X 5, X 9, et X 3 : X 1 = a; X 4 = Si non t: X 2 Sinon e; X 4 Fsi X 2 = b; Si non u : Si non v : c; X 2 Sinon W Fsi Sinon d; X 4 Fsi Aucune élimination ne peut être faite dans ce nouveau système.

Programmation procédurale Transformations � Arsac REn-->D (1977) • Dérécursifier X 2: Soit une équation récursive : Xi<-¨-fi(X 1. . . . Xi. . Xn , W ) dépendant de Xi (récursivité), et peut être des autres variables X et de W. Une équation récursive peut être remplacée par l'équation équivalente suivante : Xi = {fi ((X 1)+1, . . !0, . . . . (Xn )+1, W+1 )} Cette transformation rend non récursive une équation, après quoi le processus de substitution peut reprendre.

Programmation procédurale Transformations � Arsac REn-->D (1977) • X 2 = Répeter b; Si non u : Si non v: c; !0 Sinon W+1 Fsi Sinon d; (X 4) +1 Fsi Finrépéter

Programmation procédurale Transformations � Arsac REn-->D (1977) • X 4 devient : X 4 = Si non t : Répéter b; Si non u : Si non v: c; !0 Sinon W+1 Fsi Sinon d; (X 4) +1 Fsi Finrépéter Sinon e; X 4 fsi

Programmation procédurale Transformations � Arsac REn-->D (1977) • Récursifier X 4 : X 4 = Répéter Si non t : Répeter b; Si non u : Si non v: c; !0 Sinon W+2 Fsi Sinon d; !1 Fsi Finrépéter Sinon e; !0 fsi Finrépéter

Programmation procédurale Transformations � Arsac REn-->D (1977) • Enfin X 1 devient : a; Répéter Si non t : Répeter b; Si non u : Si non v: c; !0 Sinon W+2 Fsi Sinon d; !1 Fsi Finrépéter Sinon e; !0 fsi Finrépéter

Programmation procédurale Transformations � Arsac REn-->D (1977) • Remplaçons w par !0 : a; Répéter Si non t : Répeter b; Si non u : Si non v: c; Exit(0) Sinon Exit(2) Fsi Sinon d; Exit(1)Fsi Finrépéter Sinon e; Exit(0) fsi Finrépéter

Programmation procédurale Transformations 1. Ramshaw(1988) • Préservation de la structure du programme. • C'est à dire éliminer tous les "GOTO" et les étiquettes vers lesquelles ils se branchent en insérant des instructions de sortie et des boucles "Repeat-Endloop" tout en gardant le reste du programme inchangé. • Donc plus de lisibilité.

Programmation procédurale Transformations � Ramshaw(1988) • Soit l'exemple suivant : action 1; action 2; if test 3 then Goto G endif; _ action 4; action 5; G: action 6;

Programmation procédurale Transformations � Ramshaw(1988) • Il se transforme comme suit : action 1; action 2; Repeat if test 3 then Exit L endif; action 4; action 5; Exit L ; Endloop : L action 6;

Programmation procédurale Transformations � Williams and Chen(1985) • Par identification de schémas • Cette méthode a été proposée par Williams et Chen dans un article intitulé "Restructuring Pascal programs containing Goto statements" • son principe est basé sur la constitution d'une bibliothèque de schémas équivalents. • Un schéma pour une forme de branchement.

Programmation procédurale Transformations � Williams and Chen(1985) • On procède par identification dans le programme proposé d'un schéma type puis remplacement de celui-ci par le schéma équivalent sans branchement. • La méthode repose sur une triade ( T 1, T 2, T 3 ) d'ensembles de transformations de base, et procède en utilisant la structure hiérarchique de Pascal

Programmation procédurale Transformations 1. R vers B transformation • Procédé sémantique : technique basée sur la sémantique de la récursion. • 1. Définir la zone de donnée = paramètres appelée par valeur, adresse de retour. • 2. Définir les points d'appels et de retour. On suppose qu'il existe un premier appel dans le programme principal.

Programmation procédurale Transformations � R vers B transformation 3. Chaque Appel se traduit par : - Empiler la zone de donnée - préparer la nouvelle - se brancher au début de la procédure 4. Chaque retour se traduit par : - récupérer l'adresse de retour, Ret. - dépiler la zone de donnée - se brancher à Ret.