PROGRAMMATION ET ENSEIGNEMENT PRO1026 Logique Contenu du cours

PROGRAMMATION ET ENSEIGNEMENT PRO-1026

• Logique Contenu du cours 2 – Introduction – Logique propositionnelle – Logique et langage VB. NET • Notes de cours (site ftp UQTR)

• Introduction Logique • Ce document introduit les concepts de bases de la logique mathématique. • Pour être capable de comprendre les concepts les plus avancés de la logique mathématique, il est nécessaire de bien maîtriser la logique propositionnelle.

Logique • Introduction – Les notions de logique servent à la création des expressions logiques utilisées pour spécifier par exemple la condition de continuation d’une boucle (structure répétitive) ou la condition d’exécution du bloc d’instructions associé à une structure conditionnelle dans un programme. – Le formalisme utilisé s’exprime sous forme de langages logiques, la logique propositionnelle.

Logique • Logique propositionnelle – Cette logique est une logique très simple qui se trouve à la base de presque toutes logiques qui sont étudiées aujourd’hui. – Les éléments de bases sont des propositions (ou variables propositionnelles) qui représentent des énoncés qui peuvent être soit vrais ou faux. – La proposition p: "Marc est un étudiant" ou une proposition q: "Deux est un nombre pair". – Des propositions complexes peuvent être construites à partir des propositions en utilisant les connecteurs logiques : (“et”), (“ou”), et ¬ (négation).

Logique • Logique propositionnelle (exemple de proposition)

Logique • Logique propositionnelle (proposition) • Définition : Une proposition est une assertion (phrase éventuellement) qui ne peut qu’être Vraie ou Fausse. – Donc deux valeurs de vérités Vraie (v) et Faux (f). • Exemple : – ‘La terre est carrée’ est une assertion Fausse. – ‘Trois-Rivières est au Québec’ est une assertion Vraie.

Logique • Logique propositionnelle (opérateurs) • Il y a plusieurs façons de combiner des propositions simples de sorte à produire des propositions plus complexes. • Des connecteurs (opérateurs) comme et ( ), ou ( ), non( , ~), si … alors (implique, ), si et seulement si (équivalent à, ) • L’opérateur non opère sur une seule proposition • Les autres opérateurs opèrent sur plusieurs propositions (2 ou plus) • Pour connaître la valeur de vérité d’une proposition nous pouvons utilisé les tables de vérité.

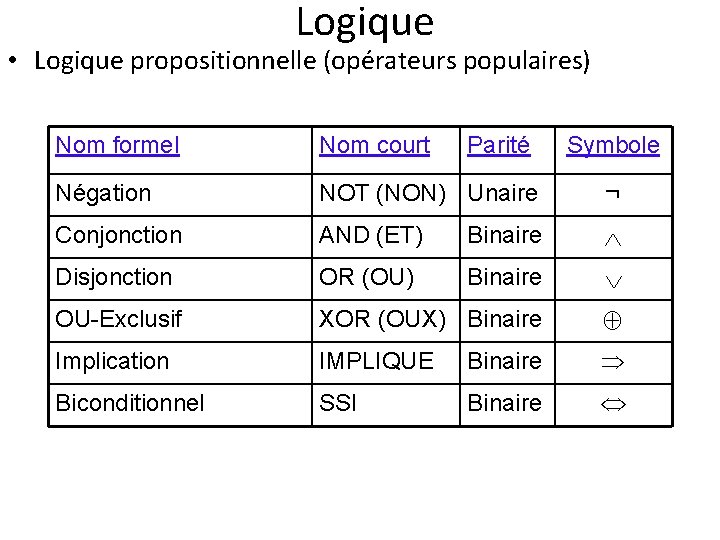
Logique • Logique propositionnelle (opérateurs populaires) Nom formel Nom court Parité Symbole Négation NOT (NON) Unaire ¬ Conjonction AND (ET) Binaire Disjonction OR (OU) Binaire OU-Exclusif XOR (OUX) Binaire Implication IMPLIQUE Binaire Biconditionnel SSI Binaire

Logique • Logique propositionnelle (opérateurs populaires) • L’opérateur de négation “¬” (NOT, NON) transforme une prop. dans sa forme logique complémentaire (négation). Ex: SI p = “J’ai les cheveux blanc. ” ALORS ¬p = “Je n’ai pas les cheveux blanc. ” • Table de vérité du NOT/NON: T : ≡ True; F : ≡ False “: ≡” “est défini comme” Opérande Résultat

Logique • Logique propositionnelle (opérateurs populaires) • L’opérateur de conjonction “ ” (AND, ET) combine deux propositions pour former leur conjonction logique. ND Ex: SI p=“J’irai à Québec. ” et q=“J’irai au Château Frontenac. ”, alors p q=“J’ira à Québec et au Château Frontenac. ” Rappel: “ ” pointe vers le haut comme un “A”, et correspond au “ ND”

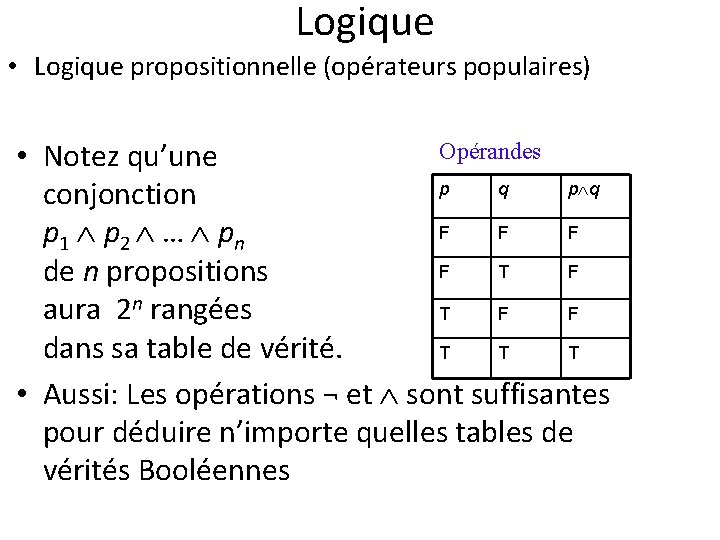
Logique • Logique propositionnelle (opérateurs populaires) Opérandes • Notez qu’une p q conjonction F F F p 1 p 2 … pn F T F de n propositions aura 2 n rangées T F F dans sa table de vérité. T T T • Aussi: Les opérations ¬ et sont suffisantes pour déduire n’importe quelles tables de vérités Booléennes

Logique • Logique propositionnelle (opérateurs populaires) • L’opérateur de disjonction “ ” (OR/OU) combine deux propositions pour former une disjonction logique. p=“Mon ordinateur a une bonne carte graphique. ” q=“Mon ordinateur a un CPU performant. ” p q=“Mon ordinateur a soit une bonne carte graphique, or (ou) mon ordinateur a un CPU performant. ”

Logique • Logique propositionnelle (opérateurs populaires) • Notez que p q signifie que p est VRAI, ou q est vrai, ou les deux sont vraies! • Cette opération est aussi appelée ou inclusif, et inclus la possibilité que p et q soient VRAIES. Notez la différence avec AND

Logique • Logique propositionnelle (opérateurs populaires) • Posons p = “Il a plue la nuit dernière”, q = “Le balai mécanique a lavée la rue cette nuit”, r = “La rue est mouillée ce matin. ” Tranduisez chaque proposition: “Il n’a pas plue la nuit dernière. ” ¬p = r ¬p = “La rue est mouillée mais il n’a pas plue” ¬r p q = “Soit que la rue n’était pas mouillée, ou il a plue la nuit dernière, ou la rue a été lavée cette nuit. ”

Logique • Logique propositionnelle (opérateurs populaires) • L’opérateur OU-Exclusif “ ” (XOR) combine deux propositions formant leur “OU exclusif” logique. p = “J’obtiendrai un A+ dans ce cours, ” q = “J’abandonnerai ce cours, ” p q = “Je vais soit avoir un A+ dans ce cours, ou j’abandonnerai (mais pas les deux)”

Logique • Logique propositionnelle (opérateurs populaires) • Notez que p q veut dire que p est vrai, ou q est vrai, mais pas les deux! • Cette opération est appelée OU-exclusif, puisqu’elle exclus la possibilité que p et q soient VRAIES. Notez la différence avec le OR.

Logique • Logique propositionnelle (opérateurs populaires) • Notez qu’en français le “ou” peut être ambïgu en regard des cas inclusif et exclusif “Joe est un plombier ou Joe est un politicien. ” “Joe a eu un A dans son cours de plomberie ou Joe a eu un B dans ce cours. ” • Besoin du contexte pour désambiguïser le sens des propositions

Logique • Logique propositionnelle (opérateurs populaires: implication) Hypothèse Conclusion • L’ implication p q signifie que p implique q. Ex: , posons p = “Vous étudiez beaucoup. ” q = “Vous obtenez une bonne cote. ” p q = “Si vous étudiez beaucoup, vous obtiendrai Alors une bonne cote. ”

Logique • Logique propositionnelle (opérateurs populaires: implication) • p q est faux seulement quand p est VRAI mais que q n’est pas VRAI (not true). • p q ne veut pas dire que p a causé q • p q ne requiert pas que p ou q soit VRAIE • EX: “(1=0) Dumbo l’éléphant vole” est VRAIE Le seul cas FAUX

Logique • Logique propositionnelle (opérateurs populaires: implication) • Considérons une phrase comme, – “Si je regarde CNN demain, il tombera de la grêle” • En logique, cette phrase est considérée VRAIE tant que je ne regarde pas CNN ou qu’il grêle. • Mais, dans une conversation normale, ce genre d’affirmation est déconcertante et questionnable.

Logique • Logique propositionnelle (opérateurs populaires: implication) • Une phrase en langage courant “SI p ALORS q” peut signifier implicitement: – – “Dans toutes les situations possibles, p implique q. ” SI p est VRAI ALORS q est aussi VRAI. SI p n’est pas VRAI ALORS q est FAUX. Il existe une relation entre, l’hypothèse et la conclusion. • Ce n’est pas le cas en logique. – p q signifie ¬p V q • Ex. : “Si vous avez 100 au final, vous aurez A+” – Si vous avez 100, vous attendez à avoir un A+ (1 1=1) – Sinon, vous pourriez avoir un A+ quand même (0 1=1) – Par contre, si vous avez un 100 et n’avez pas un A+, vous sentirez probablement lésé (1 0 = 0)

Logique • Logique propositionnelle (opérateurs populaires: implication) • “Si ce cours ne se termine jamais, Alors le soleil se lèvera demain. ” True or False? • “Si lundi est un jour de la semaine, Alors Je suis un singe. ” True or False? • “Si 1+1=6, Alors Trump est président. ” True or False? • “Si la Suisse est un fromage, Alors je suis plus riche que Warren Buffet. ” True or False?

Logique • Logique propositionnelle (biconditionnelle/équivalence ) • Une forme biconditionelles p q est vraie si la proposition p est vraie et si la proposition q est vraie. Nous dirons p SSI q. p = “Obama gagne les élections de 2008. ” q = “Obama sera président jusqu’en 2012. ” p q = “Obama gagne les élections de 2008, SSI, Obama sera président jusqu’en 2012. ” 2008 2012 Yes we can!

Logique • Logique propositionnelle (biconditionnelle ) • p q signifie que p et q ont la même valeur de vérité. • Notez que cette table de vérité est l’opposée du XOR Donc, p q est équivalent ¬(p q) • p q ne veut pas dire que p et q sont VRAIES, ou que chacune est la cause de l’autre, ou découlent d’une cause commune.

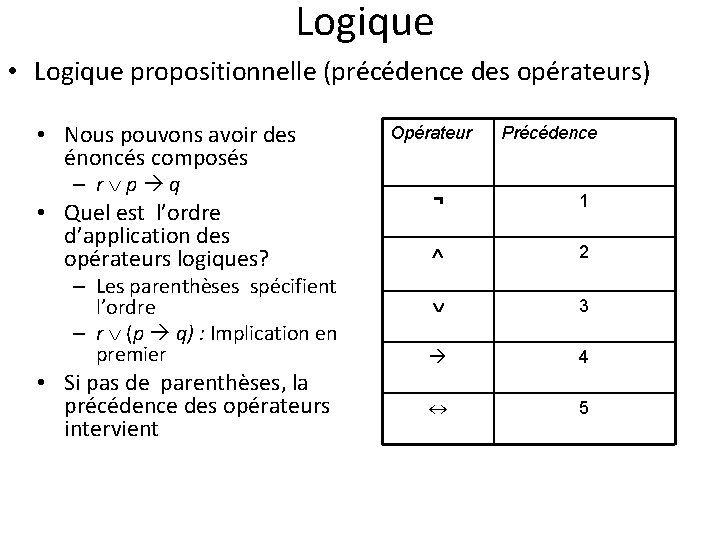
Logique • Logique propositionnelle (précédence des opérateurs) • Nous pouvons avoir des énoncés composés – r p q • Quel est l’ordre d’application des opérateurs logiques? – Les parenthèses spécifient l’ordre – r (p q) : Implication en premier • Si pas de parenthèses, la précédence des opérateurs intervient Opérateur Précédence ¬ 1 2 3 4 5

Logique • Logique propositionnelle (sommaire des opérateurs) • Table de vérité des opérateurs logiques vus jusqu’à maintenant.

Logique • Logique propositionnelle (table de vérité et propositions plus complexes) • Par exemple, considérons la proposition (A B) ( B C) où A, B et C sont des propositions. • Cette proposition complexe est construite à partir de propositions moins complexes.

Logique • Logique propositionnelle (table de vérité et propositions plus complexes) • Table de vérité correspondante: A B C (A B) B v v f f v f v f v v f f f f v v (A B) ( B C) f f v f v v v f f f v f

Logique • Logique propositionnelle (table de vérité et propositions plus complexes) Remarques • Le nombre de combinaisons dépend du nombre de propositions de départ. • Si nous avons 2 propositions nous aurons alors une table de vérité de 4 combinaisons. Si nous avons 3 propositions alors nous aurons 8 combinaisons. • En fait si le nombre de propositions est n alors le nombre de combinaisons est 2 * 2 … n fois (autrement dit 2 n)

Logique • Logique propositionnelle (table de vérité et propositions plus complexes) Définitions • Une proposition complexe est construite à partir de propositions initiales au moyen de la conjonction, de la disjonction et de la négation. • Si x et y sont des propositions alors (x), x, (x) (y) et (x) (y) sont aussi des propositions.

Logique • Logique propositionnelle (table de vérité et propositions plus complexes) Autres remarques • La proposition A B C est équivalente à (A B) C • La proposition A B C est équivalente à ((A) (B)) C • La proposition A B est équivalente à ( A) ( B)

Logique • Logique propositionnelle (table de vérité et propositions plus complexes: Exercices) 1. Construire les tables de vérités de : (A B) A ( B) (A B) C (A B) (B C) (C A) ( A) ( B) A B C D 2. Réécrire les propositions suivantes avec le moins de parenthèses possibles : ( ((A) (B))) (C) ((A) (B)) ((C) (B)) 3. Dans quel ordre sont les opérations logiques dans cette expression : A B C A

Logique • Logique propositionnelle (Implications et équivalences: autres notions: tautologies) • Une tautologie est une proposition toujours vraie. Une tautologie sera annotée par v (vrai). • Exemples : • (A B) ( A) ( B) • A A • (A B) A • A (B A) • (A B) (B A)

Logique • Logique propositionnelle (Implications et équivalences: autres notions: tautologies) • Exemple : (A B) ( A) ( B) A B (A B) A B ( A) ( B) v v v f f v f v vf v f f f v vv v

Logique • Logique propositionnelle (Implications et équivalences: autres notions, exemple concret) Sachant que : la proposition A est ‘Tension artérielle supérieure à 11’ ( Tension > 11) la proposition B est ‘Tension artérielle inférieure à 13’ (Tension < 13) la proposition (A B) signifie alors ‘Tension artérielle supérieure à 11 et inférieure à 13’ (11 < Tension < 13 ) la proposition (A B) signifie alors ‘ Tension artérielle n’est pas supérieure à 11 et inférieure à 13’ (non (11 < Tension < 13 )) autrement dit ((Tension <= 11) ou (Tension >= 13)) la proposition A signifie ‘ Tension artérielle n’est pas supérieure à 11’ (non (Tension > 11)) autrement dit (Tension <= 11) la proposition B signifie ‘ Tension artérielle n’est pas inférieure à 13’ (non (Tension < 13)) autrement dit (Tension >= 13) la proposition ( A) ( B) signifie dès lors ‘ Tension artérielle inférieure ou égale à 11 ou Tension artérielle supérieure ou égale à 13’ ((Tension <= 11) ou (Tension >= 13))

Logique • Logique propositionnelle (Implications et équivalences: autres notions, contradiction) • Une contradiction est toujours fausse. Une contradiction sera annotée par f. • Exemples : • A A • (A B) ( A) ( B)

Logique • Logique propositionnelle (Implications et équivalences: autres notions, contradiction) • Exemples : (A B) A B v v f f v f v v v f A A v f f v ( A) (A B) ( A) ( B) (A B) ( A) ( B) f f v v A A f f v f f

Logique • Logique propositionnelle (Implications et équivalences: autres notions, tautologie) • On dit qu’une proposition A est équivalente à une proposition B si la proposition A B est une tautologie. On notera l’équivalence par v • Exemples : – (A B) ( A B) v B – A B v B A

Logique • Logique propositionnelle (Implications et équivalences: autres notions, tautologie) • Exemples : A B (A B) A ( A B) (A B) ( A B) v B v v v f f f f f v f v v f f f v

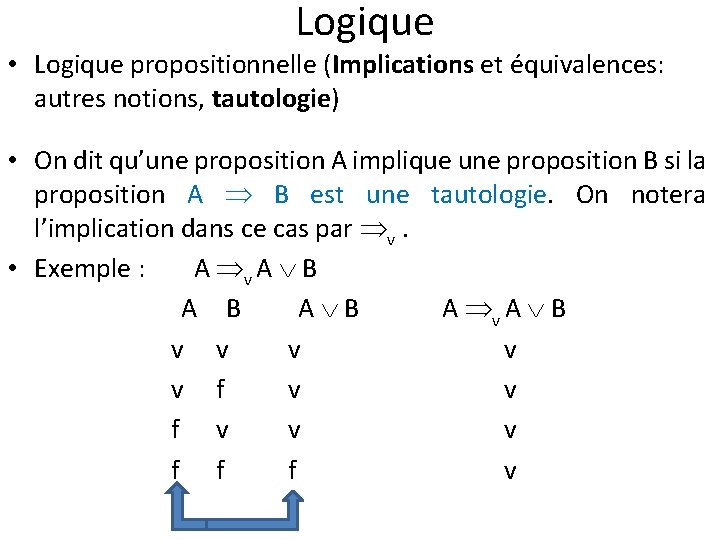
Logique • Logique propositionnelle (Implications et équivalences: autres notions, tautologie) • On dit qu’une proposition A implique une proposition B si la proposition A B est une tautologie. On notera l’implication dans ce cas par v. • Exemple : A v A B A B A v A B v v v f f f v

Logique • Logique propositionnelle (Équivalences: Exercices (voir la solution dans le fichier Exercices. Equivalence. xlsx) Trouvez les propositions qui sont équivalentes : · · · · (A B) C A (B C) B A B A (A C) (B C) B A B A A B

Logique • Logique propositionnelle (Lois/Règles d’équivalence) Similaires aux identités arithmétiques utilisées en algèbre, mais appliquées aux équivalences propositionnelles. l Peuvent être substituées entièrement ou en partie à des propositions complexes pour en prouver l’équivalence, pour les simplifier. l

Logique • Logique propositionnelle (Lois/Règles d’équivalence) p T v p p F v p l Domination: p T v T p F v F l Idempotence: p p v p l Double négation: p v p l Commutativité: p q v q p l Associativité: (p q) r v p (q r) l Identité:

Logique • Logique propositionnelle (Lois/Règles d’équivalence) l Distributivité: p (q r) v (p q) (p r) De Morgan: (p q) v p q l Tautologie/contradiction triviale (Équivalences logiques utiles: ELU) p p v T p p v F (p q) v ( p q) l

Logique • Logique et langage VB. NET – http: //www. visual-basic-tutorials. com/beginner/Conditional-and. Logical-Operators. html VB. NET offre des opérateurs Logique et Bit à bit pour implémenter des expressions logiques complexes: • Not fait une négation logique sur une expression booléenne ou une négation bit à bit sur une expression numérique. • Pour la négation booléenne le type du résultat est Booléen. • Pour la négation bit à bit, le type du résultat est le même que celui de l’expression sauf si l’expression est de type Decimal, le résultat sera de type Long.

Logique • Logique et langage VB. NET – http: //www. visual-basic-tutorials. com/beginner/Conditional-and. Logical-Operators. html VB. NET offre des opérateurs Logique et Bit à bit pour implémenter des expressions logiques complexes: • And effectue une conjonction logique sur deux expressions logiques ou une conjonction bit à bit sur deux expressions numériques. • L’opérateur And évalue toujours les deux expressions, l’opérateur And. Also n’évaluerait pas la seconde expression si la première était fausse.

Logique • Logique et langage VB. NET – http: //www. visual-basic-tutorials. com/beginner/Conditional-and. Logical-Operators. html VB. NET offre des opérateurs Logique et Bit à bit pour implémenter des expressions logiques complexes: • Or effectue une disjonction logique sur deux expressions logiques ou une disjonction bit à bit sur deux expressions numériques. • L’opérateur Or évalue toujours les deux expressions, l’opérateur Or. Else n’évaluerait pas la seconde expression si la première était vraie.

Logique • Logique et langage VB. NET – http: //www. visual-basic-tutorials. com/beginner/Conditional-and. Logical-Operators. html VB. NET offre des opérateurs Logique et Bit à bit pour implémenter des expressions logiques complexes: • Xor effectue une exclusion logique sur deux expressions logiques ou une exclusion bit à bit sur deux expressions numériques. • L’opérateur Xor évalue toujours les deux expressions.

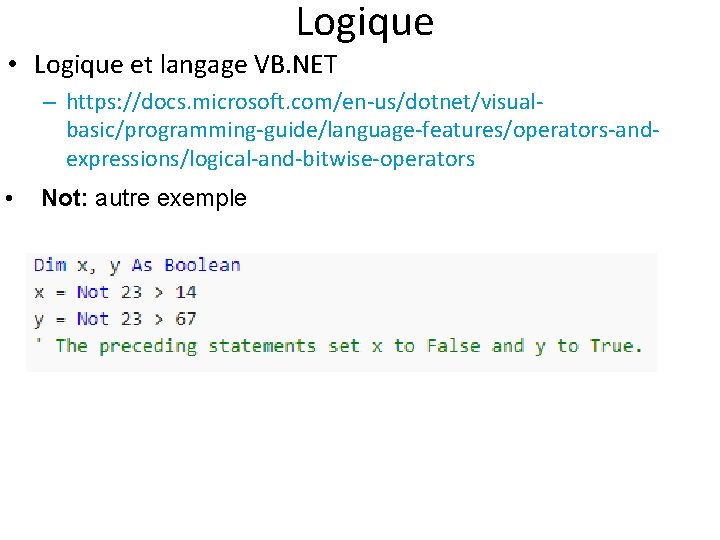
Logique • Logique et langage VB. NET – https: //docs. microsoft. com/en-us/dotnet/visualbasic/programming-guide/language-features/operators-andexpressions/logical-and-bitwise-operators • Not: autre exemple

Logique • Logique et langage VB. NET – https: //docs. microsoft. com/en-us/dotnet/visualbasic/programming-guide/language-features/operators-andexpressions/logical-and-bitwise-operators • And, Or, Xor: autres exemples

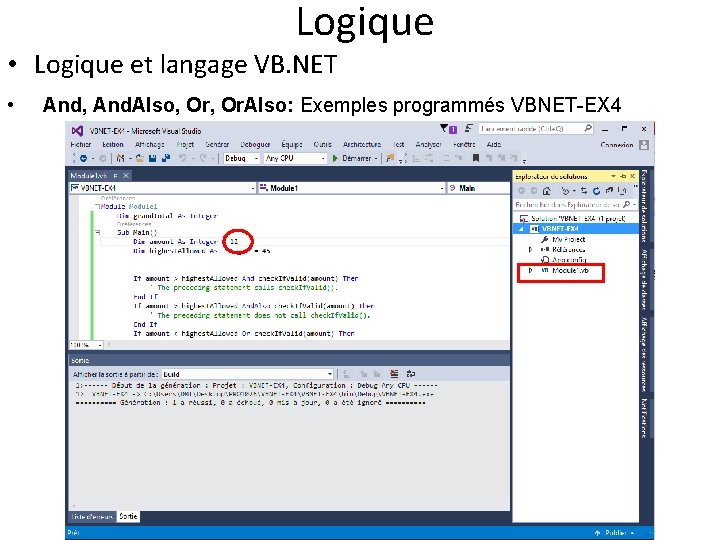
Logique • Logique et langage VB. NET – https: //docs. microsoft. com/en-us/dotnet/visualbasic/programming-guide/language-features/operators-andexpressions/logical-and-bitwise-operators • And, And. Also, Or. Also: Exemples programmés VBNETEX 4 • Cette application est de type console • Avant de tester (exécuter) l’application, veuillez d’abord modifier manuellement la valeur de la variable amount (ex: 12 ou 16) dans le fichier Module 1. vb • Pour exécuter l’application faire ctrl-F 5

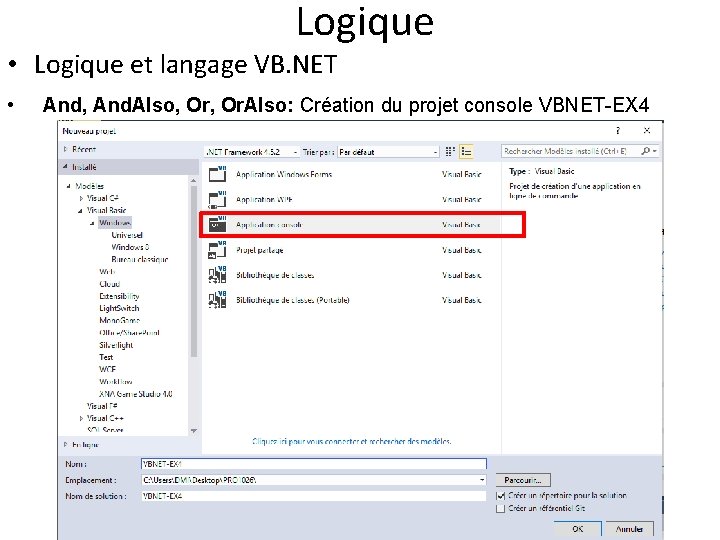
Logique • Logique et langage VB. NET • And, And. Also, Or. Also: Création du projet console VBNET-EX 4

Logique • Logique et langage VB. NET • And, And. Also, Or. Also: Exemples programmés VBNET-EX 4