Programao Linear Teoria e Modelagem Matemtica Prof Antnio

Programação Linear Teoria e Modelagem Matemática Prof. Antônio Sérgio Coelho (coelho@deps. ufsc. br) Prof. Sérgio Fernando Mayerle (mayerle@deps. ufsc. br)

Programação Linear Sumário – Parte I § § § Exemplo introdutório Modelagem conceitual e matemática Solução gráfica Dificuldades adicionais Lista de exercícios adicionais

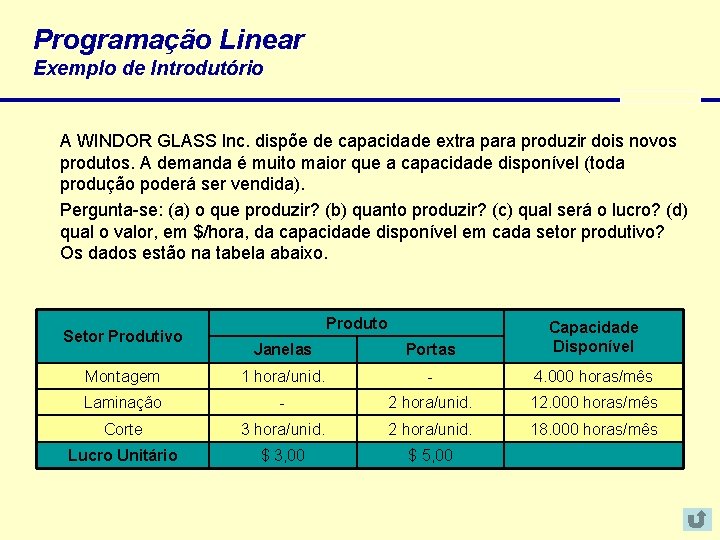
Programação Linear Exemplo de Introdutório A WINDOR GLASS Inc. dispõe de capacidade extra para produzir dois novos produtos. A demanda é muito maior que a capacidade disponível (toda produção poderá ser vendida). Pergunta-se: (a) o que produzir? (b) quanto produzir? (c) qual será o lucro? (d) qual o valor, em $/hora, da capacidade disponível em cada setor produtivo? Os dados estão na tabela abaixo. Produto Janelas Portas Capacidade Disponível Montagem 1 hora/unid. - 4. 000 horas/mês Laminação - 2 hora/unid. 12. 000 horas/mês Corte 3 hora/unid. 2 hora/unid. 18. 000 horas/mês Lucro Unitário $ 3, 00 $ 5, 00 Setor Produtivo

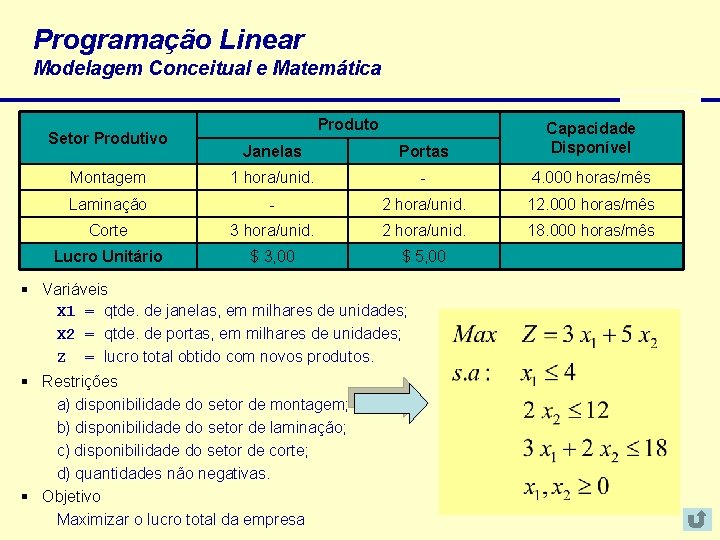
Programação Linear Modelagem Conceitual e Matemática Produto Janelas Portas Capacidade Disponível Montagem 1 hora/unid. - 4. 000 horas/mês Laminação - 2 hora/unid. 12. 000 horas/mês Corte 3 hora/unid. 2 hora/unid. 18. 000 horas/mês Lucro Unitário $ 3, 00 $ 5, 00 Setor Produtivo § Variáveis X 1 = qtde. de janelas, em milhares de unidades; X 2 = qtde. de portas, em milhares de unidades; Z = lucro total obtido com novos produtos. § Restrições a) disponibilidade do setor de montagem; b) disponibilidade do setor de laminação; c) disponibilidade do setor de corte; d) quantidades não negativas. § Objetivo Maximizar o lucro total da empresa

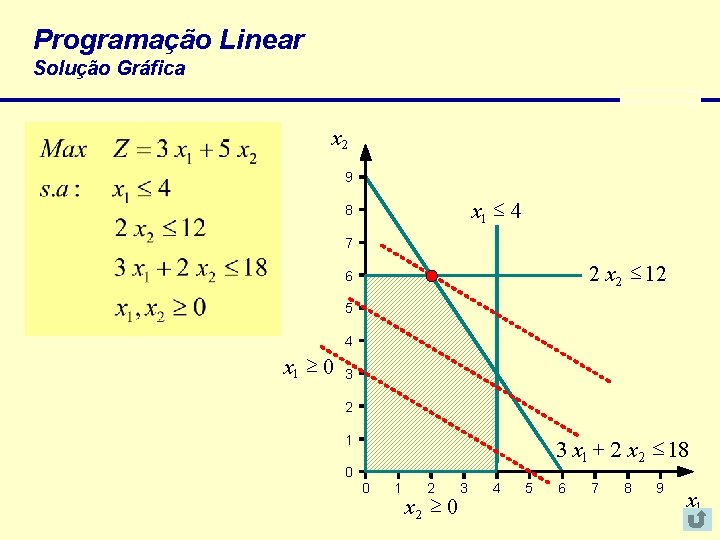
Programação Linear Solução Gráfica x 2 9 x 1 £ 4 8 7 2 x 2 £ 12 6 5 4 x 1 0 3 2 3 x 1 + 2 x 2 £ 18 1 0 0 1 2 x 2 0 3 4 5 6 7 8 9 x 1

Programação Linear Dificuldades Adicionais ao Problema. . . § O que fazer se além de portas e janelas a WINDOR puder fabricar, também, mesas e armários? Resolver graficamente o problema torna-se inviável. . . É necessário usar métodos numéricos mais eficazes e eficientes. § Quantos produtos diferentes uma fábrica pode produzir? 5, 100, 1000, . . . § Quantos setores de produção uma fábrica possui? 5, 100, 1000, . . . § E se existem restrições adicionais em relação ao uso de matéria-prima, energia, estoques, mão-de-obra, cadeia de suprimento e distribuição? Outros modelos, mais complexos, poderão ser formulados. . .

Programação Linear Lista de Exercícios de Formulação § § § § § Produção Logística Mistura Finanças e investimentos Carregamento de navios Corte de chapas e barras Aquisição de máquinas Problemas dinâmicos Câmbio § § § Alguns do problemas acima apresentam variáveis discretas que somente podem assumir valores do conjunto de inteiros, e em casos mais particulares o conjunto de inteiros se limita a {0, 1}. § § § Estratégia militar Engenharia estrutural Operação de dutos Dimensionamento de linhas de produção Alocação de mão-de-obra Programação de operações Controle de emissão de poluentes

Programação Linear Sumário – Parte II § § § Forma padrão Relações de equivalência Suposições da Programação Linear Propriedades Estrutura do método Simplex

Programação Linear Forma Padrão (1)

Programação Linear Forma Padrão (2)

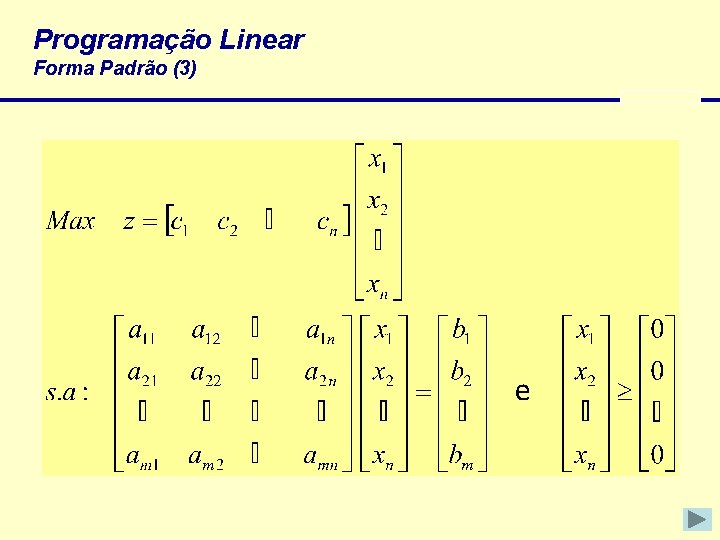
Programação Linear Forma Padrão (3)

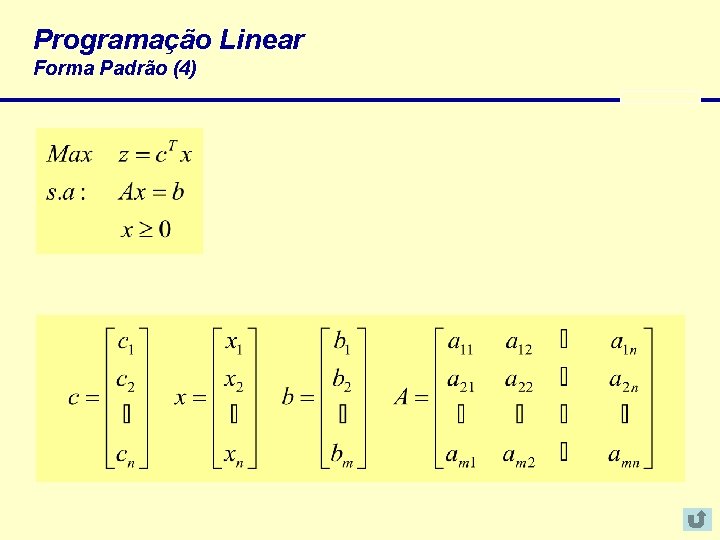
Programação Linear Forma Padrão (4)

Programação Linear Relações de Equivalência (1) § Qualquer que seja a estrutura do PPL, sempre é possível transformá-lo no formato padrão apresentado. § Relação entre maximização e minimização

Programação Linear Relações de Equivalência (2) § Relação entre inequações e equações

Programação Linear Relações de Equivalência (3) § Tratamento de limites de variáveis

Programação Linear Suposições § Proporcionalidade Custos e quantidades de recursos consumidos na produção são proporcionais às quantidades produzidas § Aditividade Custos totais e quantidades totais de recursos são determinados pela soma de custos e recursos consumidos na produção de todos items § Divisibilidade É possível produzir quantidades fracionárias de cada um dos produtos § Certeza Todos os parâmetros do modelo são determinados e conhecidos § Perspectiva das suposições Existe a possibilidade de todas estas suposições não serem verdadeiras.

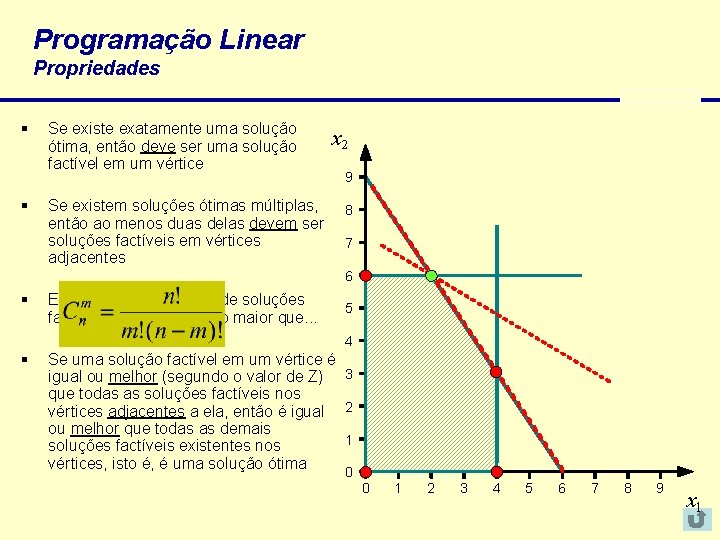
Programação Linear Propriedades § § Se existe exatamente uma solução ótima, então deve ser uma solução factível em um vértice Se existem soluções ótimas múltiplas, então ao menos duas delas devem ser soluções factíveis em vértices adjacentes x 2 9 8 7 6 § Existe um número finito de soluções factíveis em vértices, não maior que. . . 5 4 § Se uma solução factível em um vértice é igual ou melhor (segundo o valor de Z) 3 que todas as soluções factíveis nos vértices adjacentes a ela, então é igual 2 ou melhor que todas as demais 1 soluções factíveis existentes nos vértices, isto é, é uma solução ótima 0 0 1 2 3 4 5 6 7 8 9 x 1

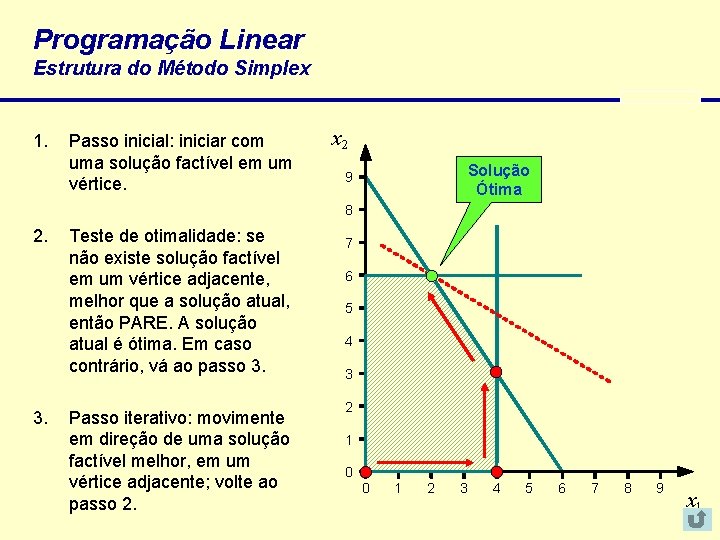
Programação Linear Estrutura do Método Simplex 1. Passo inicial: iniciar com uma solução factível em um vértice. x 2 Solução Ótima 9 8 2. 3. Teste de otimalidade: se não existe solução factível em um vértice adjacente, melhor que a solução atual, então PARE. A solução atual é ótima. Em caso contrário, vá ao passo 3. Passo iterativo: movimente em direção de uma solução factível melhor, em um vértice adjacente; volte ao passo 2. 7 6 5 4 3 2 1 0 0 1 2 3 4 5 6 7 8 9 x 1

Programação Linear Sumário – Parte III § § § Solução inicial viável (caso trivial) Método Simplex na forma tableau Algoritmo Exemplo da WINDOR Método Simplex na forma matricial Formulação matemática Exemplo da WINDOR Obtenção da solução inicial viável (caso não trivial) Inclusão de variáveis artificiais Solução inicial pelo método das duas fases Solução inicial pelo método do M-grande

Programação Linear Solução Inicial Viável (caso trivial) Caso trivial a) variáveis não negativas b) restrições com limite superior Solução variáveis nulas folgas iguais ao RHS

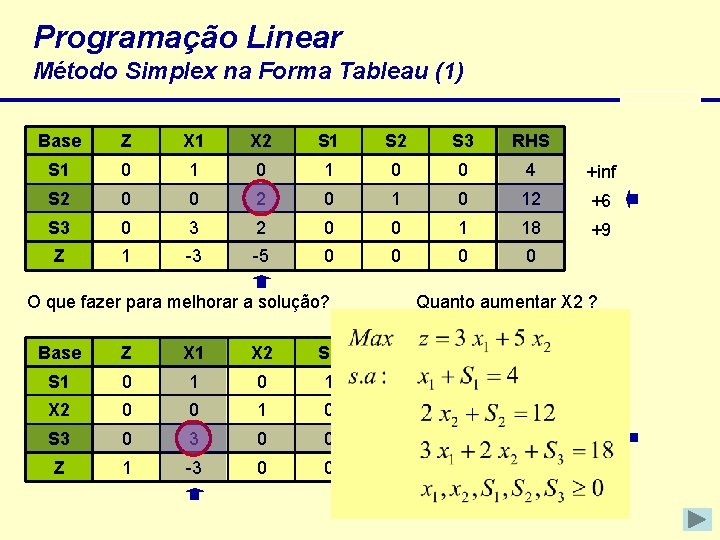
Programação Linear Método Simplex na Forma Tableau (1) Base Z X 1 X 2 S 1 S 2 S 3 RHS S 1 0 1 0 0 4 +inf S 2 0 0 2 0 12 +6 S 3 0 3 2 0 0 1 18 +9 Z 1 -3 -5 0 0 O que fazer para melhorar a solução? Quanto aumentar X 2 ? Base Z X 1 X 2 S 1 S 2 S 3 RHS S 1 0 1 0 0 4 +4 X 2 0 0 1/2 0 6 +inf S 3 0 0 -1 1 6 +2 Z 1 -3 0 0 5/2 0 30

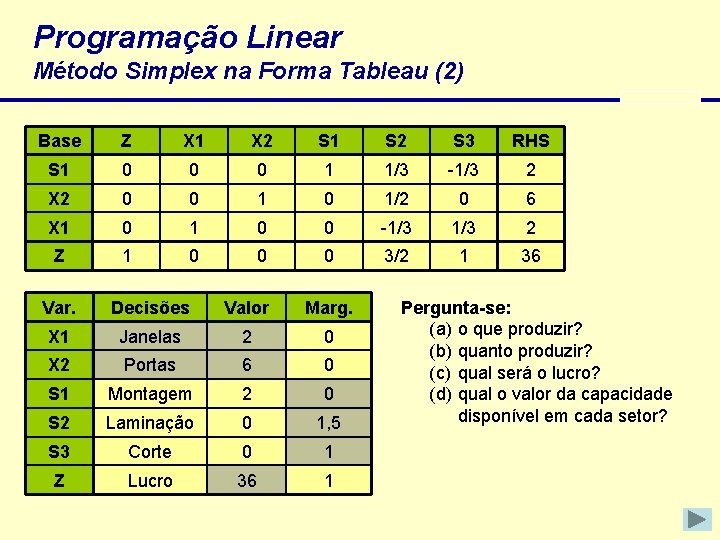
Programação Linear Método Simplex na Forma Tableau (2) Base Z X 1 X 2 S 1 S 2 S 3 RHS S 1 0 0 0 1 1/3 -1/3 2 X 2 0 0 1/2 0 6 X 1 0 0 -1/3 2 Z 1 0 0 0 3/2 1 36 Var. Decisões Valor Marg. X 1 Janelas 2 0 X 2 Portas 6 0 S 1 Montagem 2 0 S 2 Laminação 0 1, 5 S 3 Corte 0 1 Z Lucro 36 1 Pergunta-se: (a) o que produzir? (b) quanto produzir? (c) qual será o lucro? (d) qual o valor da capacidade disponível em cada setor?

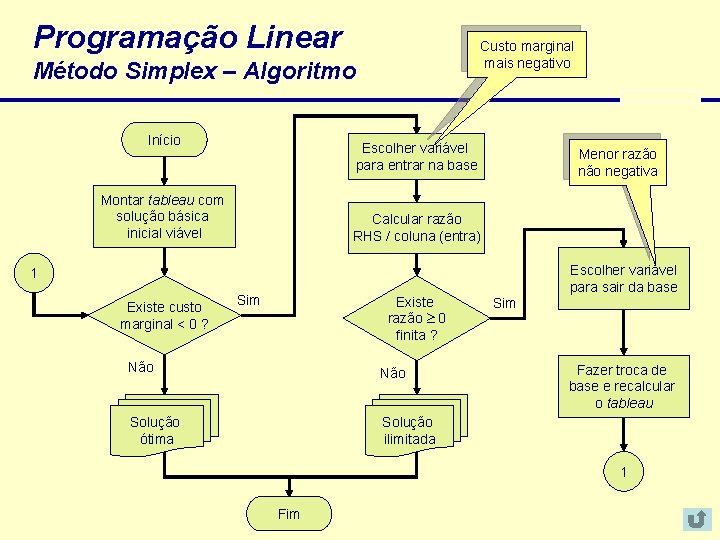
Programação Linear Custo marginal mais negativo Método Simplex – Algoritmo Início Escolher variável para entrar na base Montar tableau com solução básica inicial viável Menor razão negativa Calcular razão RHS / coluna (entra) Escolher variável para sair da base 1 Existe custo marginal < 0 ? Sim Existe razão 0 finita ? Não Solução ótima Solução ilimitada Sim Fazer troca de base e recalcular o tableau 1 Fim

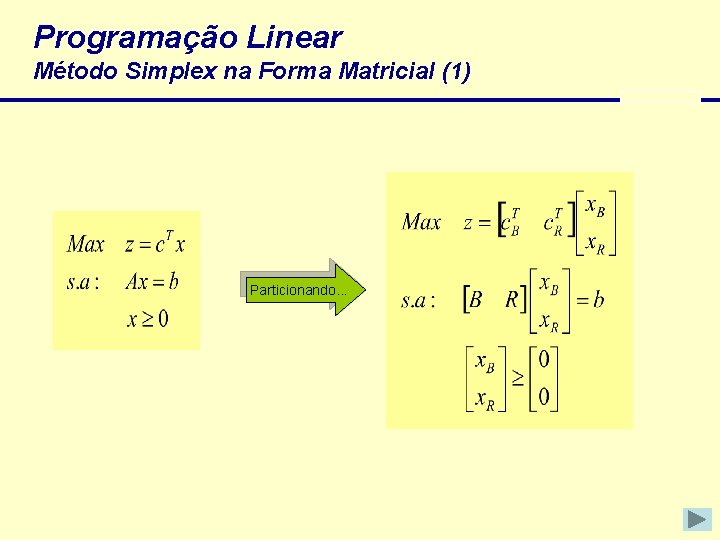
Programação Linear Método Simplex na Forma Matricial (1) Particionando. . .

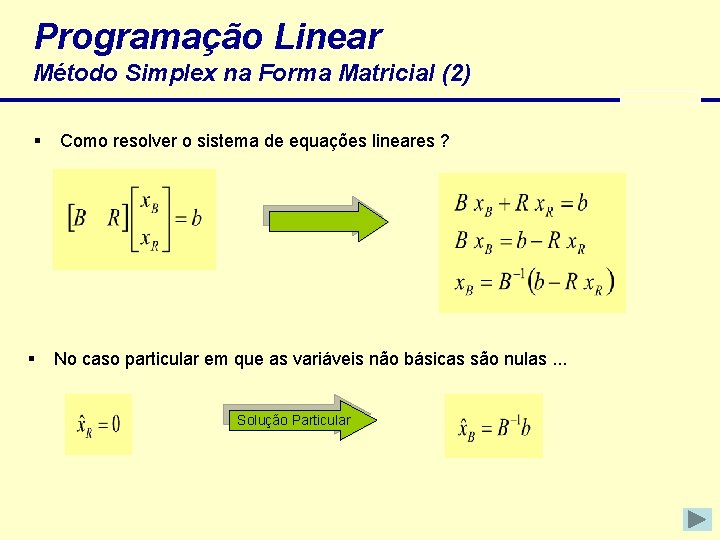
Programação Linear Método Simplex na Forma Matricial (2) § § Como resolver o sistema de equações lineares ? No caso particular em que as variáveis não básicas são nulas. . . Solução Particular

Programação Linear Método Simplex na Forma Matricial (3) § § E o valor da função objetivo ? No caso particular em que as variáveis não básicas são nulas. . . Solução Particular

Programação Linear Método Simplex na Forma Matricial (4) § Resumindo, até aqui tem-se. . . § É possível melhorar o valor da função objetivo ? . . .

Programação Linear Método Simplex na Forma Matricial (5) § Como melhorar. . . Escolher para aumentar (entrar na base) uma variável não básica associada a uma componente positiva do vetor

Programação Linear Método Simplex na Forma Matricial (6) § Aumentar a k-ésima variável não básica (escolhida). . . até quanto ? Escolher para sair da base uma variável básica associada ao menor valor calculado.

Programação Linear Método Simplex na Forma Matricial (7) § Resumo. . . Solução Teste de entrada Teste de saída

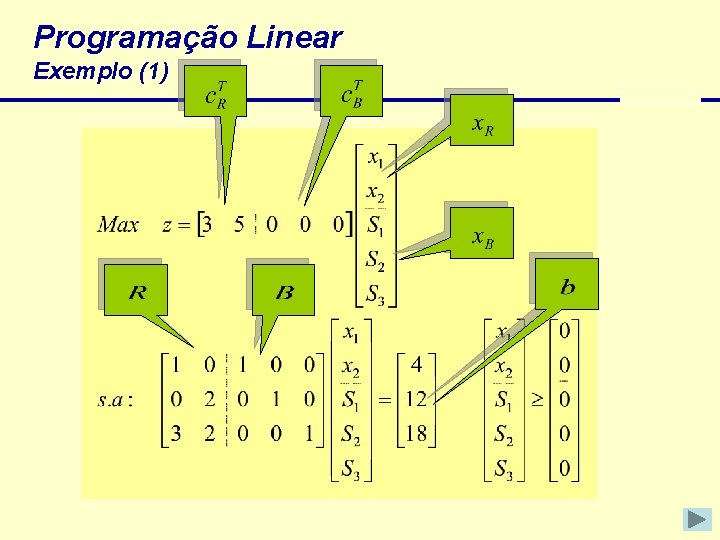
Programação Linear Exemplo (1)

Programação Linear Exemplo (1. a) 1 a. Iteração

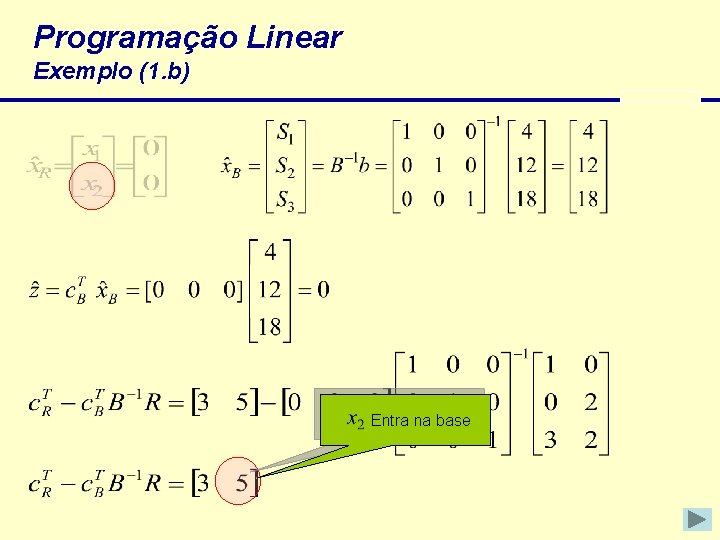
Programação Linear Exemplo (1. b) Entra na base

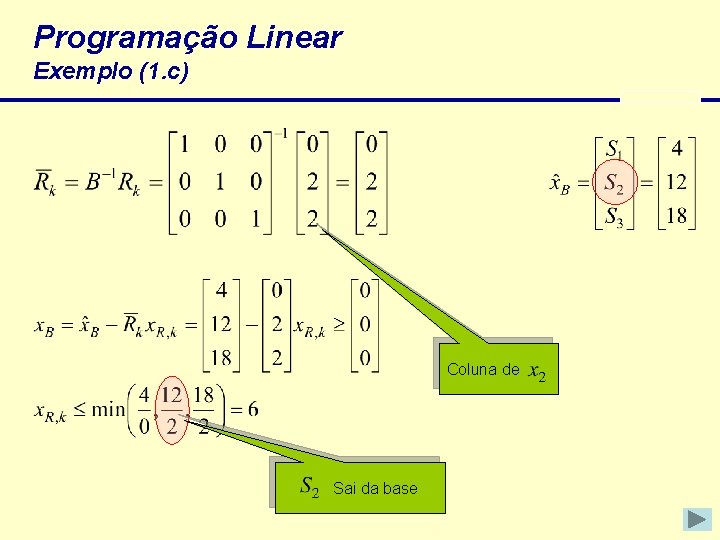
Programação Linear Exemplo (1. c) Coluna de Sai da base

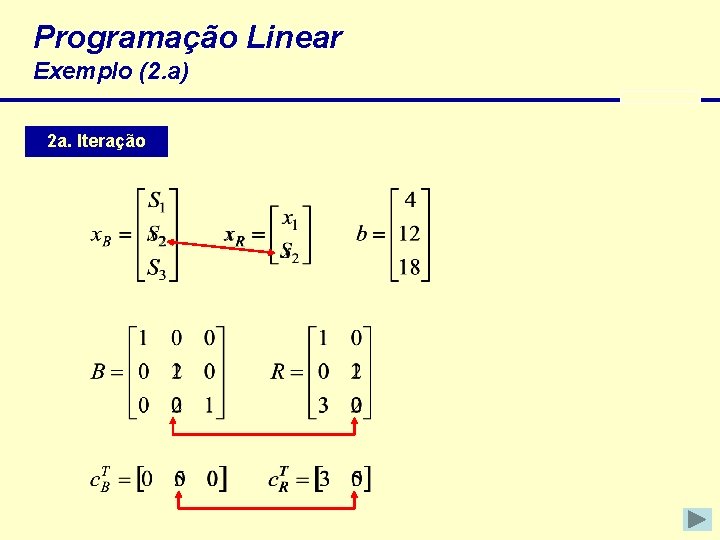
Programação Linear Exemplo (2. a) 2 a. Iteração

Programação Linear Exemplo (2. b) Entra na base

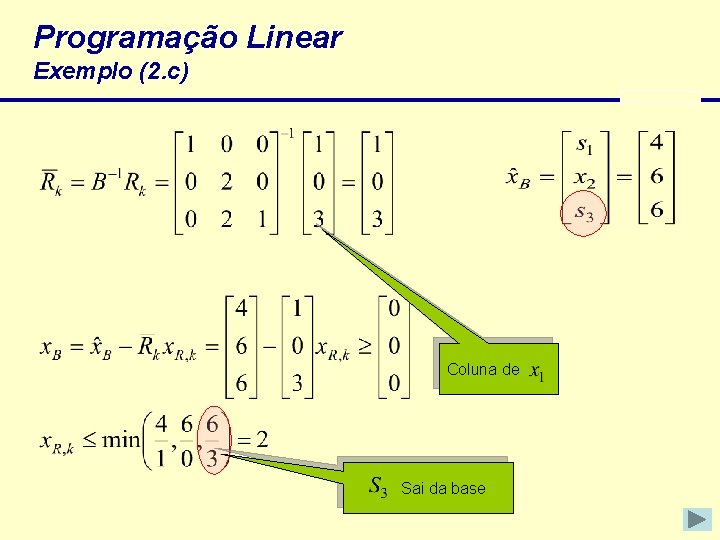
Programação Linear Exemplo (2. c) Coluna de Sai da base

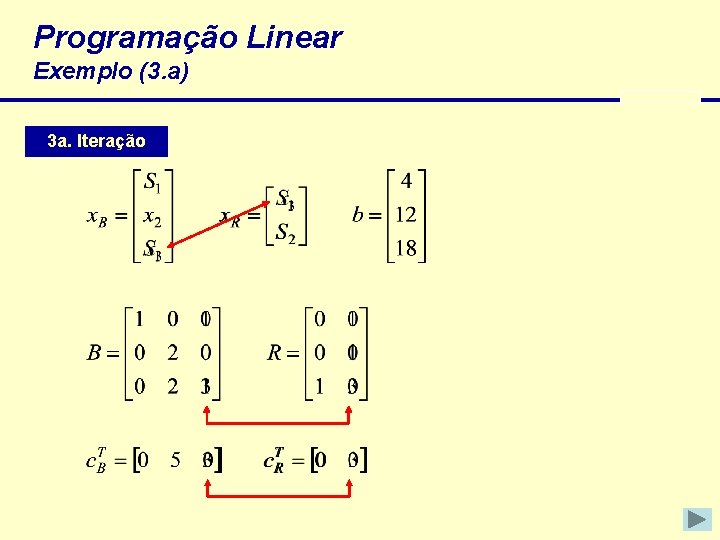
Programação Linear Exemplo (3. a) 3 a. Iteração

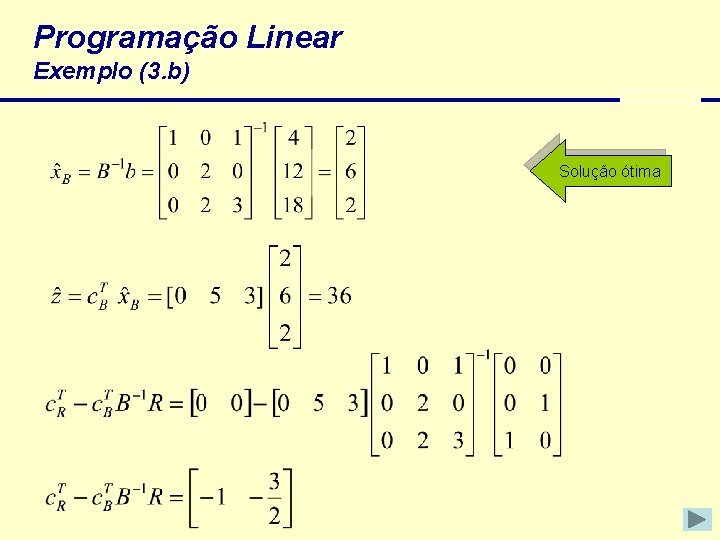
Programação Linear Exemplo (3. b) Solução ótima

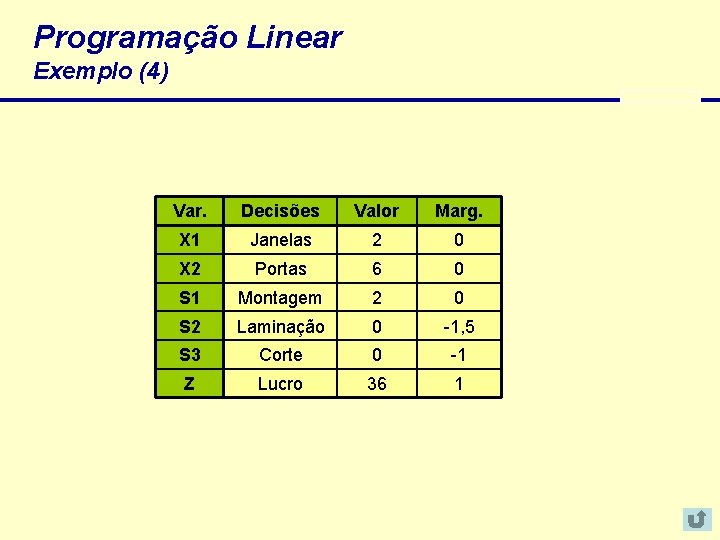
Programação Linear Exemplo (4) Var. Decisões Valor Marg. X 1 Janelas 2 0 X 2 Portas 6 0 S 1 Montagem 2 0 S 2 Laminação 0 -1, 5 S 3 Corte 0 -1 Z Lucro 36 1

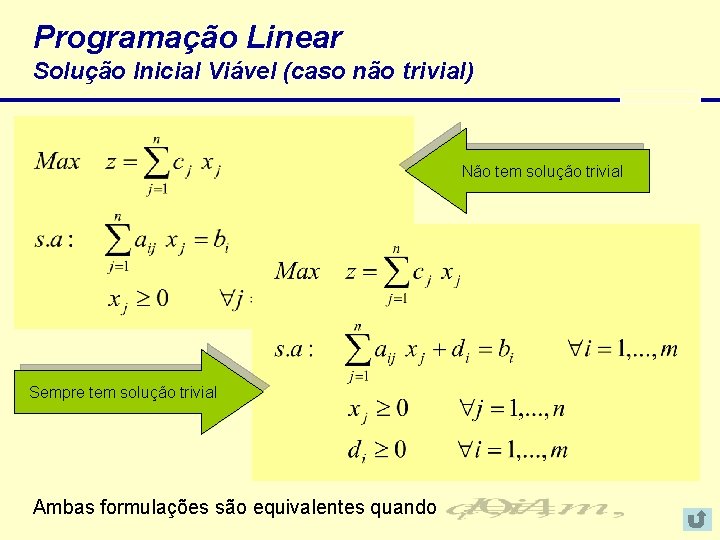
Programação Linear Solução Inicial Viável (caso não trivial) Não tem solução trivial Sempre tem solução trivial Ambas formulações são equivalentes quando

Programação Linear Solução Inicial Viável – Método do M-grande

Programação Linear Solução Inicial Viável – Método das 2 Fases Fase 1 Resolver o problema da fase 1 usando as variáveis artificiais para formar uma base inicial viável. Se w = 0, então uma solução inicial viável foi obtida para o problema. Fase 2 Se w = 0, usar solução ótima da fase 1 como solução inicial viável para a fase 2.

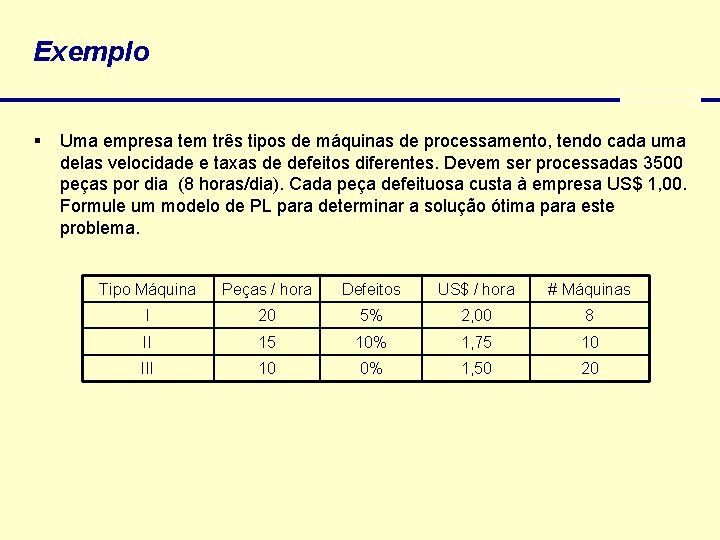
Exemplo § Uma empresa tem três tipos de máquinas de processamento, tendo cada uma delas velocidade e taxas de defeitos diferentes. Devem ser processadas 3500 peças por dia (8 horas/dia). Cada peça defeituosa custa à empresa US$ 1, 00. Formule um modelo de PL para determinar a solução ótima para este problema. Tipo Máquina Peças / hora Defeitos US$ / hora # Máquinas I 20 5% 2, 00 8 II 15 10% 1, 75 10 III 10 0% 1, 50 20