Programacin de Memoria Compartida open MP El Modelo

Programación de Memoria Compartida open. MP

El Modelo de Memoria Compartida Los procesadores interactuan uno con otro mediante variables compartidas. Open. MP es el estandar para programación de memoria compartida.

¿Que es open. MP? • open. MP es una especificación para una implementación portable de paralelismo en FORTRAN y C/C++. • La especificación provee directivos de compilador, rutinas de biblioteca que se pueden usar para controlar paralelismo.

Paralelismo Fork/Join • Inicialmente solamente el hilo maestro está activo • El hilo maestro ejecuta el código secuencial • Fork: El hilo maestro crea hilos adicionales para ejecutar el código paralelo • Join: Al finalizar de código paralelo, los hilos creados mueren o se suspendienden

Ejemplo #include <omp. h> #include <stdio. h> int main (int argc, char *argv[]) { #pragma omp parallel printf(“Hello worldn”); return 0; }

El Modelo de Memoria Compartida vs. el Modelo que Pasa Mensajes (#1) • El modelo de memoria compartida – El número de hilos es 1 al principio y al final y cambia dinámicamente durante de la ejecutación del programa • El Modelo que pasa mensajes – Todos los procesos estan activos durante de la ejecutacion del programa.

Paralelización Incremental • Un programa secuencial es un caso especial de un programa de memoria compartida • Paralelización incremental es el procesos de convertir un programa secuencial a un programa paralelo poco a poco

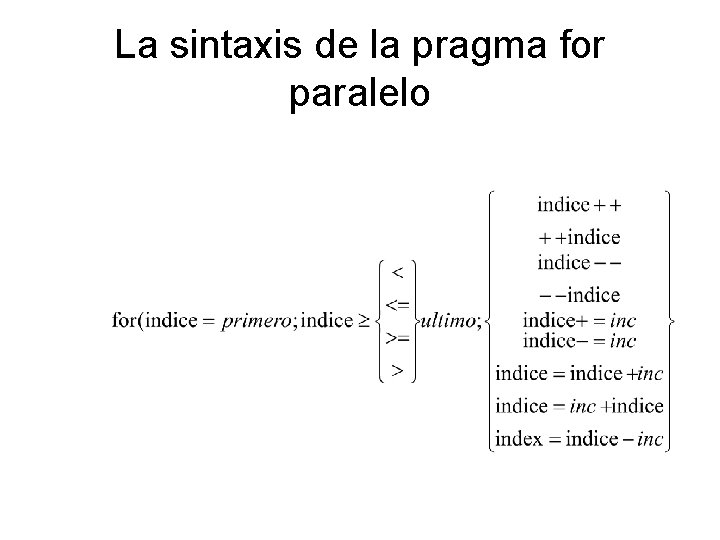
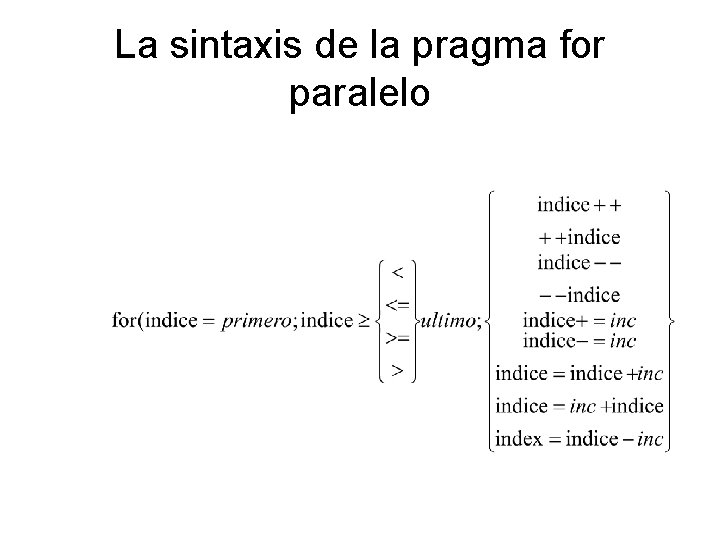
Un Bucle for Paralelo • Las iteraciones de un bucle for se pueden ejecutar en paralelo si ninguna iteración depende de otra anterior. • Ejemplos: Las iteraciones de - for (i=first; i<size; i += prime; marked[i]=1) se pueden ejecutar en paralelo, pero -for (i=1; i<=n; i++) suma += suma + v[i] no

Pragmas • Una pragma en C o C++ es un directivo al compilador. • La sintaxis es #pragma omp <el resto de la pragma> Ejemplo: #pragma omp parallel for es una directriz que dice al compilador que trate a paralelizar el bucle for que sigue

La Pragma for Paralelo #pragma omp parallel for (i = 0; i < N; i++) a[i] = b[i] + c[i]; • El compilador tiene que verificar que cuando se ejecuta, habrá disponible la información necesaria para llevar a cabo las iteraciones

La sintaxis de la pragma for paralelo

El Contexto de Ejecutación • Todo hilo tiene un contexto de ejecutación, que consiste del espacio de direcciones que el hilo puede acesar • El contexto de ejecutación incluye variables estáticas, estructuras dinámicamente asignadas, y variables en el “run-time stack”

“Variables Compartidas y Variables Privadas • Una variable compartida tiene la misma dirección en el contexto de ejecutación de cada hilo. • Una variable privada tiene una dirección distinta en el contexto de ejecutación de cada hilo. • Un hilo no puede acesar las variables privadas de otro hilo.

Función omp_set_num_threads • Se usa para asignar el número de hilos a ser activos en secciones paralelas del código • Se puede llamar en varios puntos del programa void omp_set_num_threads (int t)

omp_get_thread_num() • Todo hilo tiene una identificación que es el número del hilo • omp_get_thread_num() devuelve el número del hilo

Función omp_get_num_procs • Devuelve el número de procesadores fisicos que están dispondible para el uso del programa paralelo int omp_get_num_procs (void)

Hello World • #include <omp. h> • #include <stdio. h> • • int main (int argc, char *argv[]) { • int p, th_id; • p=omp_get_num_procs(); • omp_set_num_threads(p); • #pragma omp parallel private(th_id); • { • th_id = omp_get_thread_num(); • printf("Hello World from thread %dn", th_id); • } • return 0; • }

Pragmas - REPASO • Una pragma en C o C++ es un directivo al compilador. • La sintaxis es #pragma omp <el resto de la pragma> Ejemplo: #pragma omp parallel for es una directriz que dice al compilador que trate a paralelizar el bucle for que sigue

La sintaxis de la pragma for paralelo

Ejemplo 1 #pragma omp parallel for (i=0; i<(int) sqrt(x); i++) a[i] = 2. 3*I; if (i < 10) b[i]=a[i];

Ejemplo 2 flag = 0; for (i=0; (i<n) & (!flag); i++){ a[i] = 2. 3*i; if (a[i] < b[i]) flag = 1; No se puede paralelizar el bucle pues no no satisface el requisito de sintaxis.

Ejemplo 3 for (i=0; i<n; i++) { a[i] = foo(i); if (a[i] < b[i]) break; No se puede paralelizar un bucle cuyo cuerpo contiene break, return, o exit.

Variables privadas y compartidas • #pragma omp parallel <clausula> bloque • La clausula puede ser private (lista de variables) shared (lista de variables) y otras.

Variables privadas y compartidas(2) • Una variable compartida tiene la misma dirección en el contexto de ejecutación de cada hilo • Una variable privada tiene una dirección distinta en el contexto de ejecutación de cada hilo • Cada variable en el cuerpo de un bucle paralelo, excepto la variable de iteración, que no se especifica como privada es compartida.

Ejemplo //Despues de ejecutar del siguiente código, debe ser cierto que a[i] <= b[i] para todo i #pragma omp parallel for (i=0; i<n; i++) if (a[i] > b[i]) {temp=a[i]; a[i]=b[i]; b[i]=temp; } ¿Funciona este código?

Ejemplo(continuado) • No funciona correctamente, pues la variable temp debe ser privada • //El código correcto #pragma omp parallel for private(temp) for (i=0; i<n; i++) if (a[i] > b[i]) {temp=a[i]; a[i]=b[i]; b[i]=temp; }

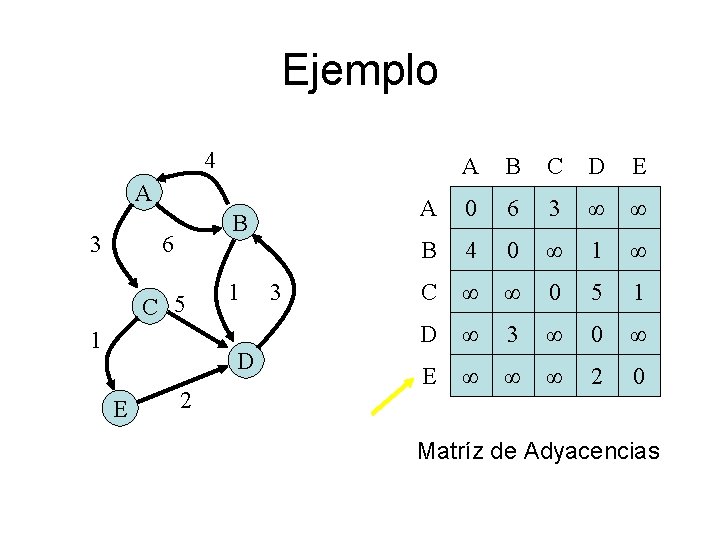
Grafos con Pesos • Un grafo dirigido en la cual hay asociado con cada arista un número positivo (el “peso”) se llama un grafo dirigido con pesos. • El largo de una trayectoria de un vértice u a otro vértice v es la suma de los pesos de las aristas que componen la trayectoria.

El Problema de Todos Pares Distancias mas Cortas • Dado un grafo dirigido con pesos, ¿cuales son las trayectorias de largos mínimos (es decir “distancias mas cortas”) entre todos los pares de vértices?

La Matríz de Adyacencias • Representar un grafo dirigido con pesos G con n vértices por una matríz AG como sigue: • Si 1, 2, … , n son los vértices, entonces el elemento en la fila #i y la columna #j es 0 si i=j, es ∞ (un número mas grande que cualquier peso) si no hay arista de I a j, y es el peso de la arista de i a j si tal arista existe. Llamemos AG la matríz de adyacencias.

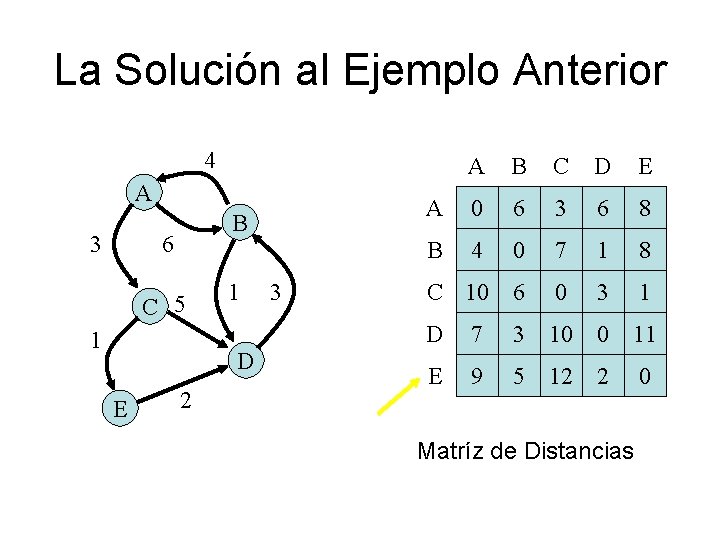
Ejemplo 4 A 3 B 6 C 5 1 1 D E 2 3 A B C D E A 0 6 3 ∞ ∞ B 4 0 ∞ 1 ∞ C ∞ ∞ 0 5 1 D ∞ 3 ∞ 0 ∞ E ∞ ∞ ∞ 2 0 Matríz de Adyacencias

El Algoritmo de Floyd for (k= 0; k<n; k++) for (i =0; i< n; i++) for (j= 0; j<n; j++) a[i, j] min (a[i, j], a[i, k] + a[k, j])

La Solución al Ejemplo Anterior 4 A 3 B 6 C 5 1 1 D E 2 3 A B C D E A 0 6 3 6 8 B 4 0 7 1 8 C 10 6 0 3 1 D 7 3 10 0 11 E 9 5 12 2 0 Matríz de Distancias

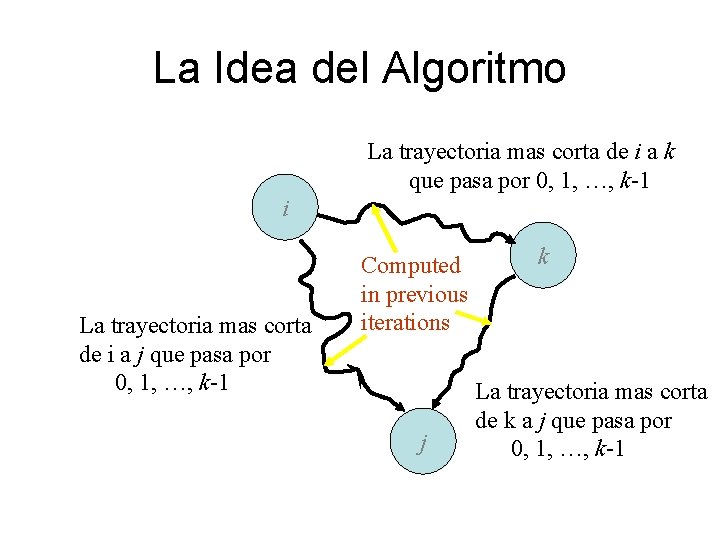
La Idea del Algoritmo La trayectoria mas corta de i a k que pasa por 0, 1, …, k-1 i La trayectoria mas corta de i a j que pasa por 0, 1, …, k-1 Computed in previous iterations j k La trayectoria mas corta de k a j que pasa por 0, 1, …, k-1

¿Como se puede paralelizar el algoritmo de Floyd? for (k= 0; k<n; k++) for (i =0; i< n; i++) for (j= 0; j<n; j++) a[i, j] min (a[i, j], a[i, k] + a[k, j]) No se puede paralelizar el primer bucle. Se puede paralelizar el segundo o el tercero. ¿Cual es mejor?

El algoritmo de Floyd paralelizado for (k= 0; k<n; k++) #pragma omp parallel for private(j) for (i =0; i< n; i++) for (j= 0; j<n; j++) a[i, j] min (a[i, j], a[i, k] + a[k, j]) Mejor paralelizar el segundo bucle en vez del tercero para evitar el costo de “fork join” repetido

Asignación Escribir un programa sequencial en C (o C++) para resolver el problema de Floyd. La entrada debe consistir de n, el número de vértices en el grafo con pesos, y la matriz de adjacencias. Esta matriz debe ser implementada como un arreglo dinámico. La entrada puede ser mediante el teclado o mediante un archivo. La salida debe consistir de un arreglo n X n en donde cada posición (i, j) contiene el peso de la trayectoria mas corta de i a j.

Arreglos Dinámicos Unidimensionales/ main() { Int i, n=10; int *A; A=(int *) malloc (n* sizeof(int)); //Ahora, A se puede usar como un arreglo ordinario. // Por ejemplo, for (i=0; i<n; i++) { A[i]=2*i; printf("%dn", A[i]); } }

Arreglos Dinámicos Bidimensionales main() { int i, j, m=4, n=3; int **B, *Bstorage; Bstorage=(int *) malloc (m*n*sizeof(int)); //asignar memoria para arreglo m. Xn B= (int **) malloc (m*sizeof(int *)); //asignar memoria para el arreglo //de apuntadores a las filas for (i=0; i<m; i++) B[i]=&Bstorage[i*n]; //Inicializar el arrego de apuntadores a las filas //Ahora podemos tratar como un m Xn arreglo ordinario. //Por ejemplo, for (i=0; i<m; i++) { for (j=0; j<n; j++) { B[i][j]=i*j; printf("%d ", B[i][j]); } printf("n"); } }

¿Como se puede paralelizar el siguiente código? x[0] = complex_function(); for (i=0; j<n; i++) { for (j=1; j<4; j++) x[j]=g(i, x[j-1]); answer[i] = x[1] – x[3]; }

Como se puede paralelizar el siguiente código: x[0] = complex_function(); for (i=0; j<n; i++) { for (j=1; j<4; j++) x[j]=g(i, x[j-1]); answer[i] = x[1] – x[3]; } Se puede hacer el bucle exterior paralelo si hacemos j y x privadas. Sin embargo, x[0] se necesita en la primera iteración del bucle interior.

firstprivate Se podría mover la inicialización de x[0] a dentro del bucle anterior, pero es caro. Mejor usar la cláusula firstprivate. x[0] = complex_function(); #pragma omp parallel for private[j] firstprivate(x) for (i-0; j<n; i++) { for (j=1; j<4; j++) x[j]=g(i, x[j-1]); answer[i] = x[1] – x[3]; }

firstprivate (cont) • Se usa para crear una variable privada que tiene su valor inicial igual al valor de la variable controlada por el hilo maestro cuando se entra el bucle. • Si un hilo cambia el valor de una variable en alguna iteración, entonces este valor será el valor de la variable en iteraciones subsecuentes

lastprivate • La secuencialmente última iteración es la última iteración que se lleva a cabo cuando el bucle se ejecuta secuencialmente • La cláusula lastprivate se usa para copiar el valor privado del hilo que ejecutó la secuencialmente última iteración a la copia del hilo maestro

Ejemplo for (i=0; i<n; i++){ x[0] = 1. 0; for (j=1; j<4; j++) x[j] = x[j-1] * (i+1); sum_of_powers[i] = x[0]+x[1]+x[2]+x[3]; } n_cubed = x[3]; No se puede predecir el valor de x[3]!

Una solución para que x[3]=n 3 #pragma omp parallel for private(j) lastprivate(x) for (i=0; i<n; i++){ x[0] = 1. 0; for (j=1; j<4; j++) x[j] = x[j-1] * (i+1); sum_of_powers[i] = x[0]+x[1]+x[2]+x[3]; } n_cubed = x[3];

La Regla Rectangulo para Computar • = ∫ 0 1 4/(1+x 2) dx • La Regla de Rectangulo consiste de estimar el area debajo de la curva y=4/(1+x 2) entre x=0 y x=1 mediante areas de rectangulos

Código para aproximar double area, pi, x; int i, n; . . . area = 0. 0; for (i = 0; i < n; i++) { x += (i+0. 5)/n; area += 4. 0/(1. 0 + x*x); } pi = area / n;

¿Como se puede paralelizar el código para aproximar a ? for (i = 0; i < n; i++) { x += (i+0. 5)/n; area += 4. 0/(1. 0 + x*x); } Si dos hilos, digamos A y B están ejecutando dos iteraciones, entonces B podria intentar a poner area al dia mientras que A está haciendo lo mismo, B podría usar el valor de area antes de que A ha terminado a poner su nuevo valor Esto se llama una “condición de carrera”

La Pragma critical • #pragma omp critical bloque de código garantiza que solamente un hilo ejecuta el bloque a la vez

Código correcto, pero no eficiente double area, pi, x; int i, n; . . . area = 0. 0; #pragma omp parallel for private(x) for (i = 0; i < n; i++) { x += (i+0. 5)/n; #pragma omp critical area += 4. 0/(1. 0 + x*x); } pi = area / n;

Ineficiente porque … Poner area al dia a dentro de una sección crítica no es eficiente ya que • Solamente un hilo puede ejecutar la asignación a la vez, es decir, es código secuencial. • El tiempo para ejecutarla puede ser una parte significativa del bucle • Por la Ley de Amdahl, esto podria limitar el speedup

Reducciones Se puede añadir una cláusula de reducción a una pragma parallel for Hay que especificar la operación y la variable Open. MP lleva cuenta de los resultados parciales y como combinarlos despues del bucle

La Cláusula reduction • La sintaxis es: reduction (<op> : <variable>) • Operadores + * & | ^ && || Suma Producto Bitwise and Bitwise or Bitwise exclusive or Logical and Logical or

El Código con la Cláusula reduction double area, pi, x; int i, n; . . . area = 0. 0; #pragma omp parallel for private(x) reduction(+: area) for (i = 0; i < n; i++) { x = (i + 0. 5)/n; area += 4. 0/(1. 0 + x*x); } pi = area / n;

Mejormiento en Rendimiento Invertiendo Bucles • Muchos fork/joins puede empeorar el rendimiento • Invertir bucles puede mejorar el rendimiento si – Hay paralelismo en el bucle interio – El bucle exterior se puede paralelizar después de la inversión. – La inversión no disminuye la razón de “cache hits”

Mejormiento en Rendimiento Ejecutando Bucles Condicionalmente • Si un bucle tiene pocas iteraciones, los gastos generales podría ser mayor que la economia de ejecutación paralela. • La cláusula if instruye al compilador determinar si el bucle se debe ejecutar en paralelo. #pragma omp parallel for if(n > 5000)

Mejormiento en Rendimiento usando la cláusula schedule • Las iteraciones de un bucles pueden variar mucho en duración. • Se puede usar una cláusula schedule para indicar como las iteraciones se asignan a los hilos. • Schedule estática: todas las iteraciones se asignan a los hijos antes de ejecutarla • Schedule dinámica: solamente algunas iteraciones se asignan al prinicipio de la ejecutación de un bucle. Las otras iteraciones se asignan a hilos que terminan sus iteraciones asignadas.

Estático vs. Dinámico • Static scheduling: • -Gastos generales menores (“low overhead”) • Dynamic scheduling – Podría exhibir un cargo de trabajo no balanceado – Gastos generales mayores – Puede reduce el imbalance de trabajo

Chunks • Un chunk es un conjunto contiguos de iteraciones que se asignan a hilos • Aumentar el tamaño de un chunk reduce los gastos generales y podría aumentar el “cache hit rate” • Disminuir el tamaño de chunk permite uno a obtener un balance mas preciso del trabajo

La Cláusula schedule • La sintaxis: schedule (<tipo>[, <chunk> ]) • Se requiere tipo, pero el tamaño del chunk es opcional • El tipo puede ser – static – dynamic – guided – runtime

Opciones para schedule • schedule(static): asignar bloques de aproximadamente n/t iteraciones contiguas a cada hilo • schedule(static, C): asignar chunks de tamaño C • schedule(dynamic): asignar dinámcamente iteracones una por una. • schedule(dynamic, C): asignar dinámcamente C iteraciones a la vez

Opciones para schedule (cont) • schedule(guided, C): asignar chunks dinámicamente. Los tamaños de los chunks decrecen dependiendo de la implementación. C es el tamaño mínimo. • schedule(guided): Lo mismo excepto 1 es el tamaño mínimo. • schedule(runtime): el tipo de schedule se escoge al tiempo de ejecutación basado en el valor de la variable omp_schedule.

Para compilar y ejecutar • Compilar: cc –openmp –o pi pi. c • Ejecutar: Hay que especificar el número de hilos con o setenv OMP_NUM_THREADS = número de hilos afuera del programa o con omp_set_num_threads( número de hilos) a dentro del programa

Otro uso del la Pragma parallel Ejemplo: ¿Como se puede optimizar lo siguiente? for (i = 0; i < m; i++) { low = a[i]; high = b[i]; if (low > high) { printf ("Exiting (%d)n", i); break; } for (j = low; j < high; j++) c[j] = (c[j] - a[i])/b[i]; } No se puede paralelizar el bucle exterion pues contiene break.

Primer Intento #pragma omp parallel private(i, j) for (i = 0; i < m; i++) { low = a[i]; high = b[i]; if (low > high) { printf ("Exiting (%d)n", i); break; } for (j = low; j < high; j++) c[j] = (c[j] - a[i])/b[i]; } Ahora, cada hilo va a ejectar todas las iteraciones del bucle interior. Nos gustaria que los hilos compartan.

Segundo Intento #pragma omp parallel private(i, j) for (i = 0; i < m; i++) { low = a[i]; high = b[i]; if (low > high) { printf ("Exiting (%d)n", i); break; } #pragma omp for (j = low; j < high; j++) c[j] = (c[j] - a[i])/b[i]; }

La pragma for • #pragma omp for <bucle for> dentro de una región paralela dice al compilador particionar las iteraciones entre los hilos

Segundo Intento Ahora hay, solamente un problema: Cada hilo va a escribir un mensaje “Exiting. . ” #pragma omp parallel private(i, j) for (i = 0; i < m; i++) { low = a[i]; high = b[i]; if (low > high) { printf ("Exiting (%d)n", i); break; } #pragma omp for (j = low; j < high; j++) c[j] = (c[j] - a[i])/b[i]; }

Tercer Intento #pragma omp parallel private(i, j) for (i = 0; i < m; i++) { low = a[i]; high = b[i]; if (low > high) { #prama omp single printf ("Exiting (%d)n", i); break; } #pragma omp for (j = low; j < high; j++) c[j] = (c[j] - a[i])/b[i]; }

La Pragma single • #pragma omp single <bloque de código> dice al compilar que solamente un solo hilo deberia ejecutar el bloque sigue.

Cuarto Intento Finalmente se puede remover la barrera al finalizar del segundo bucle #pragma omp parallel private(i, j, low, high) for (i = 0; i < m; i++) { low = a[i]; high = b[i]; if (low > high) { #prama omp single printf ("Exiting (%d)n", i); break; } #pragma omp for nowait for (j = low; j < high; j++) c[j] = (c[j] - a[i])/b[i];

La cláusula nowait • Cuando se añade a un bucle for paralelo, elimina la barrera al finalizar de un bucle.

Dos Tipos de Paralelismo de Data • La paralelización del bucles for • Ejemplos: El computo de π, el algoritmo de Floyd • Paralelismo de data mas general – la creación de una región paralela mediante la pragma omp parallel • Ejemplos: hello, satisfacer un circuito

Paralelismo Funcional • Hasta ahora hemos considerado paralelismo de data nada mas • Open. MP nos permite asignar hilos distintos a partes distintas del código (paralelismo funcional)

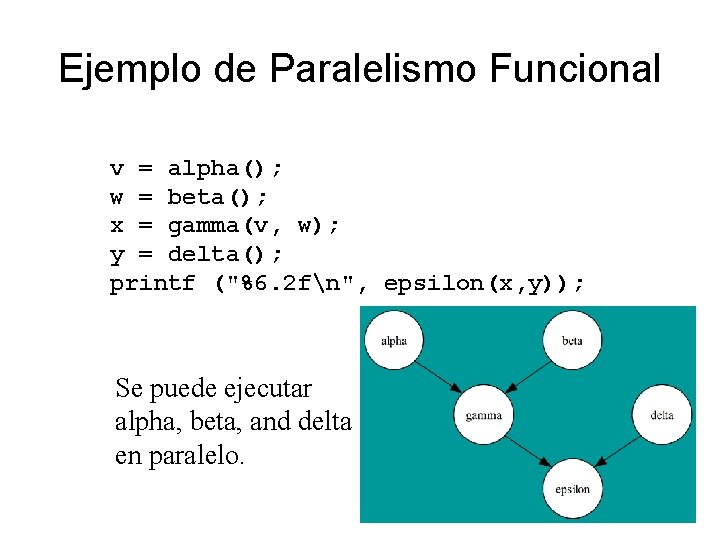
Ejemplo de Paralelismo Funcional v = alpha(); w = beta(); x = gamma(v, w); y = delta(); printf ("%6. 2 fn", epsilon(x, y)); Se puede ejecutar alpha, beta, and delta en paralelo.

La pragma parallel sections • Precede un bloque de k bloques de código que se puede ejecutar en paralelo por k hilos • La sintaxis: #pragma omp parallel sections

La pragma section • Precede cada bloque de código dentro del bloque grande • Se puede omitir para el primer bloque después de la pragma parallel sections • La sintaxis: #pragma omp section

Ejemplo de parallel sections #pragma omp parallel sections { #pragma omp section /* Optional */ v = alpha(); #pragma omp section w = beta(); #pragma omp section y = delta(); } x = gamma(v, w); printf ("%6. 2 fn", epsilon(x, y));

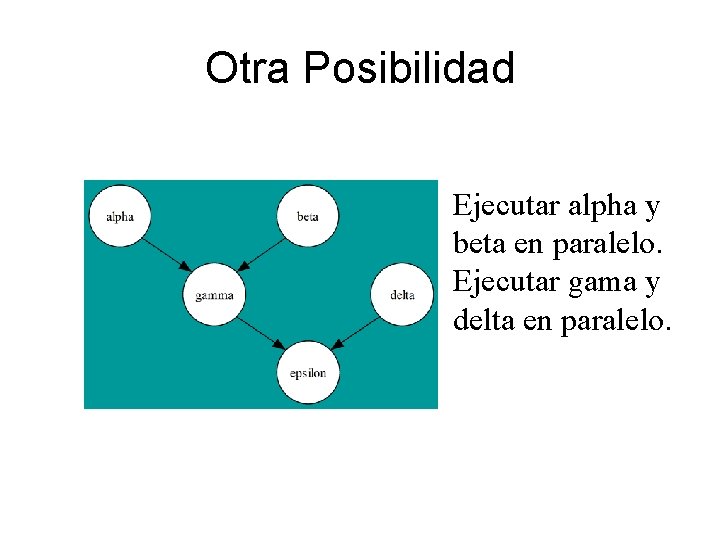
Otra Posibilidad Ejecutar alpha y beta en paralelo. Ejecutar gama y delta en paralelo.

La pragma sections • Aparece a dentro de un bloque paralelo de código • Tiene el mismo significado como la pragma parallel sections • Varias pragmas sections dentro de un bloque paralelo podría reducir los gastos de fork/join

Uso de la pragma sections #pragma omp parallel { #pragma omp sections { #pragma omp section v = alpha(); #pragma omp section w = beta(); } #pragma omp sections { #pragma omp section x = gamma(v, w); #pragma omp section y = delta(); } } printf ("%6. 2 fn", epsilon(x, y));

Como medir tiempos en open. MP • Ejemplo: double empezar, terminar; empezar=omp_get_wtime( ); … algun código terminar=omp_get_wtime(); printf(“TIEMPO=%lfn”, empezar-terminar) El resultado es en segundos.