Program verification flowchart programs Book chapter 7 History

Program verification: flowchart programs Book: chapter 7

History n n Verification of flowchart programs: Floyd, 1967 Hoare’s logic: Hoare, 1969 Linear Temporal Logic: Pnueli, Krueger, 1977 Model Checking: Clarke & Emerson, 1981

Program Verification n n n Predicate (first order) logic. Partial correctness, Total correctness Flowchart programs Invariants, annotated programs Well founded ordering (for termination) Hoare’s logic

Predicate (first order logic) n Variables, functions, predicates n Terms n Formulas (assertions)

Signature Variables: v 1, x, y 18 Each variable represents a value of some given domain (int, real, string, …). n Function symbols: f(_, _), g 2(_), h(_, _, _). Each function has an arity (number of paramenters), a domain for each parameter, and a range. f: int*int->int (e. g. , addition), g: real->real (e. g. , square root) A constant is a predicate with arity 0. n Relation symbols: R(_, _), Q(_). Each relation has an arity, and a domain for each parameter. R : real*real (e. g. , greater than). Q : int (e. g. , is a prime). n

Terms are objects that have values. n Each variable is a term. n Applying a function with arity n to n terms results in a new term. Examples: v 1, 5. 0, f(v 1, 5. 0), g 2(f(v 1, 5. 0)) n More familiar notation: sqr(v 1+5. 0)

Formulas Applying predicates to terms results in a formula. R(v 1, 5. 0), Q(x) More familiar notation: v 1>5. 0 n One can combine formulas with the boolean operators (and, or, not, implies). R(v 1, 5. 0)->Q(x) x>1 -> x*x>x n One can apply existentail and universal quantification to formulas. x Q(X) x 1 R(x 1, 5. 0) X Y R(x, y) n

A model, A proofs n n n A model gives a meaning (semantics) to a first order formula: n A relation for each relation symbol. n A function for each function symbol. n A value for each variable. An important concept in first order logic is that of a proof. We assume the ability to prove that a formula holds for a given model. Example proof rule (MP) :

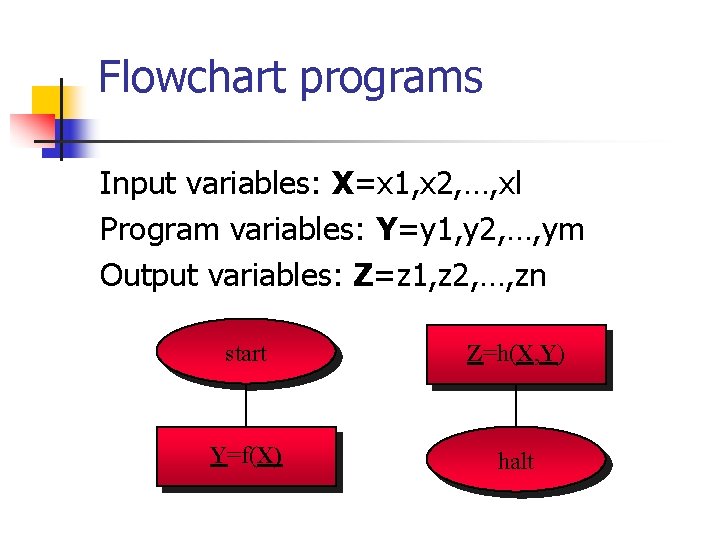
Flowchart programs Input variables: X=x 1, x 2, …, xl Program variables: Y=y 1, y 2, …, ym Output variables: Z=z 1, z 2, …, zn start Z=h(X, Y) Y=f(X) halt

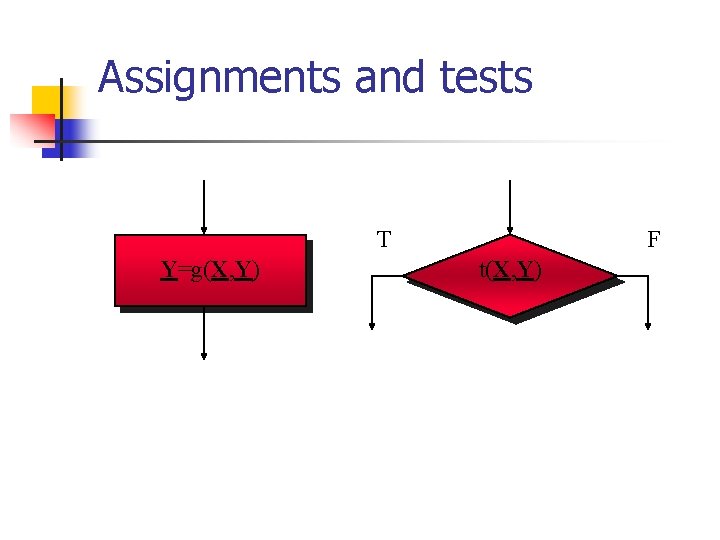
Assignments and tests T Y=g(X, Y) F t(X, Y)

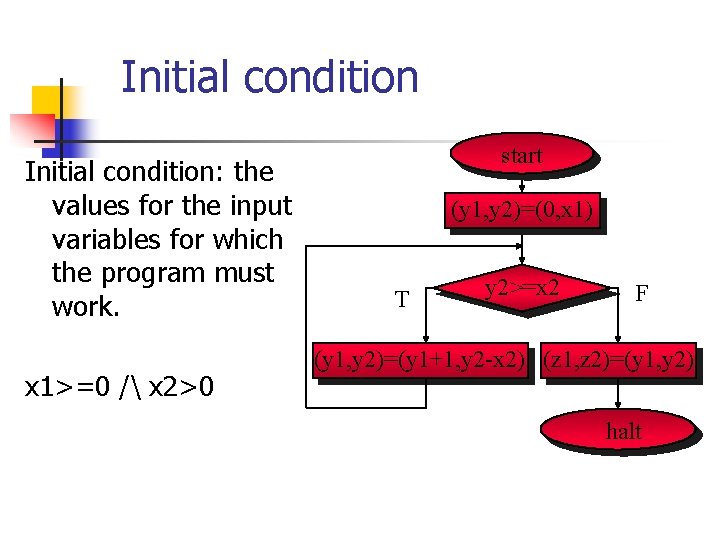
Initial condition: the values for the input variables for which the program must work. x 1>=0 / x 2>0 start (y 1, y 2)=(0, x 1) T y 2>=x 2 F (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) halt

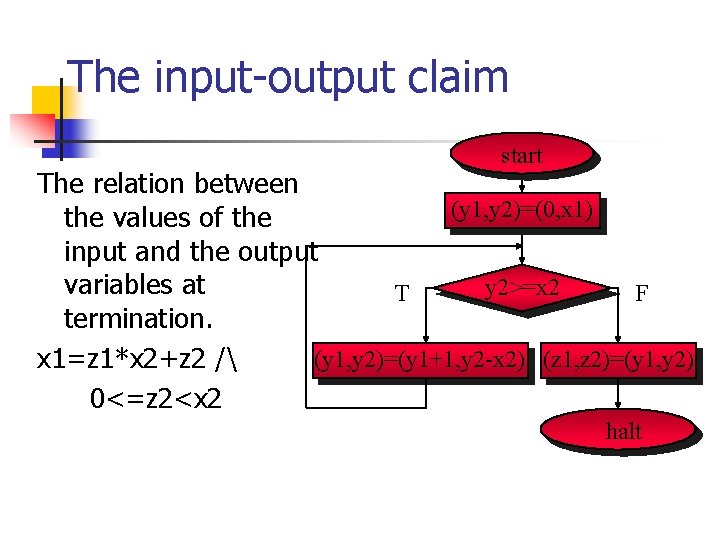
The input-output claim start The relation between (y 1, y 2)=(0, x 1) the values of the input and the output variables at y 2>=x 2 T F termination. (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) x 1=z 1*x 2+z 2 / 0<=z 2<x 2 halt

Partial correctness, Termination, Total correctness n n n Patial correctness: if the initial condition holds and the program terminates then the input-output claim holds. Termination: if the initial condition holds, the program terminates. Total correctness: if the initial condition holds, the program terminates and the input-output claim holds.

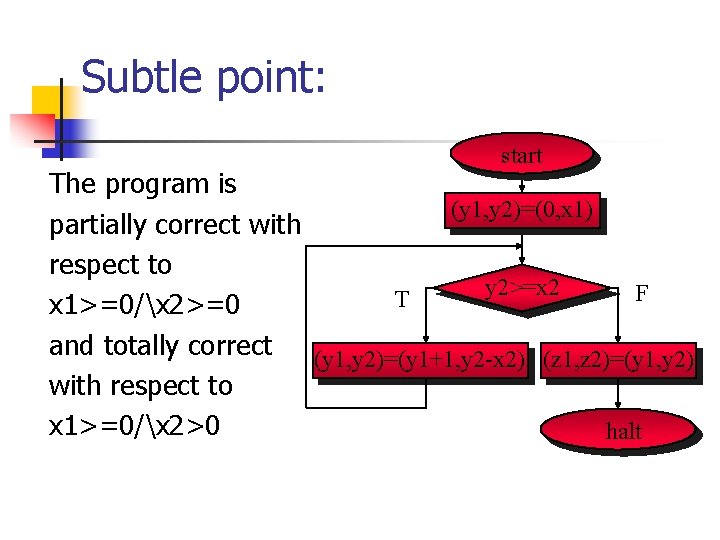
Subtle point: start The program is (y 1, y 2)=(0, x 1) partially correct with respect to y 2>=x 2 F T x 1>=0/x 2>=0 and totally correct (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) with respect to x 1>=0/x 2>0 halt

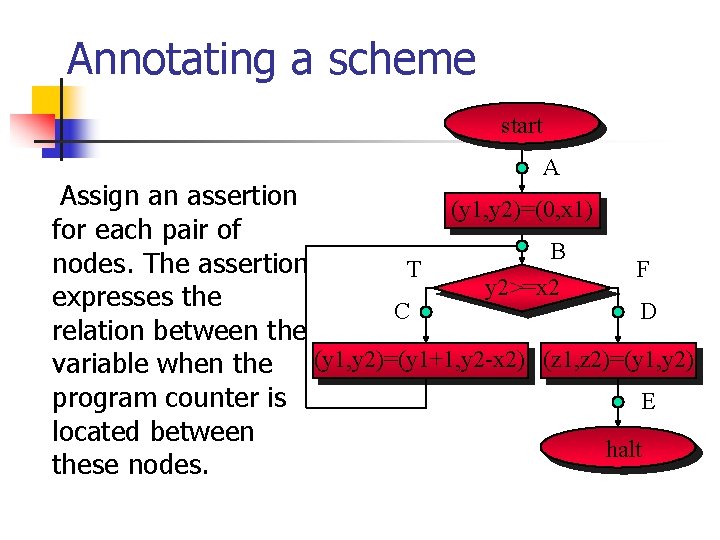
Annotating a scheme start A Assign an assertion (y 1, y 2)=(0, x 1) for each pair of B nodes. The assertion T F y 2>=x 2 expresses the C D relation between the (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) variable when the program counter is E located between halt these nodes.

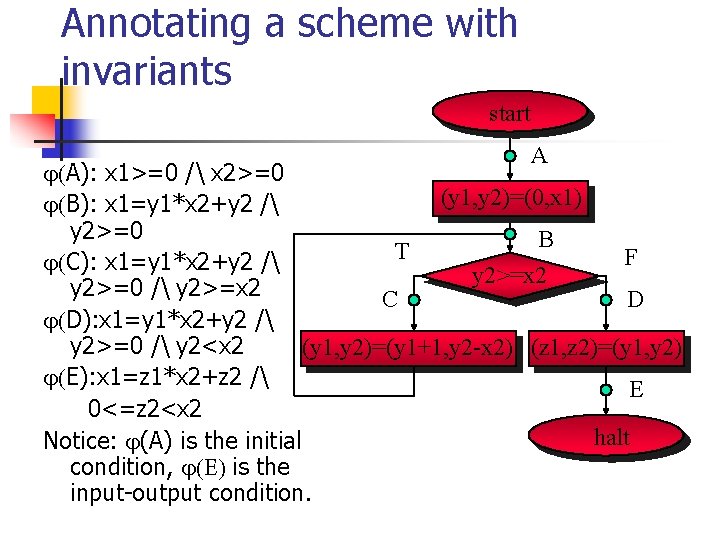
Annotating a scheme with invariants start A A): x 1>=0 / x 2>=0 (y 1, y 2)=(0, x 1) B): x 1=y 1*x 2+y 2 / y 2>=0 B T F C): x 1=y 1*x 2+y 2 / y 2>=x 2 y 2>=0 / y 2>=x 2 C D D): x 1=y 1*x 2+y 2 / y 2>=0 / y 2<x 2 (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) E): x 1=z 1*x 2+z 2 / E 0<=z 2<x 2 halt Notice: (A) is the initial condition, is the input-output condition.

Verification conditions: assignment A) B) [Yg(X, Y)] A): x 1>=0 / x 2>=0 B): x 1=y 1*x 2+y 2 / y 2>=0 A (y 1, y 2)=(0, x 1) Y=g(X, Y) B A B) [Yg(X, Y)] = x 1=0*x 2+x 1 / x 1>=0 (y 1, y 2)=(0, x 1) B

Second assignment C): x 1=y 1*x 2+y 2 / y 2>=0 / y 2>=x 2 B): x 1=y 1*x 2+y 2 / y 2>=0 B)[Yg(X, Y]: x 1=(y 1+1)*x 2+y 2 x 2 / y 2 -x 2>=0 C (y 1, y 2)=(y 1+1, y 2 -x 2) B

Third assignment D): x 1=y 1*x 2+y 2 / y 2>=0 / y 2<x 2 E): x 1=z 1*x 2+z 2 / 0<=z 2<x 2 E)[Zg(X, Y]: x 1=y 1*x 2+y 2 / 0<=y 2<x 2 D (z 1, z 2)=(y 1, y 2) E

Verification conditions: tests T B) / t(X, Y) C) B) /¬t(X, Y) D) C B): x 1=y 1*x 2+y 2 /y 2>=0 C): x 1=y 1*x 2+y 2 / y 2>=0 T / y 2>=x 2 D): x 1=y 1*x 2+y 2 / y 2>=0 C / y 2<x 2 B t(X, Y) F D B y 2>=x 2 F D

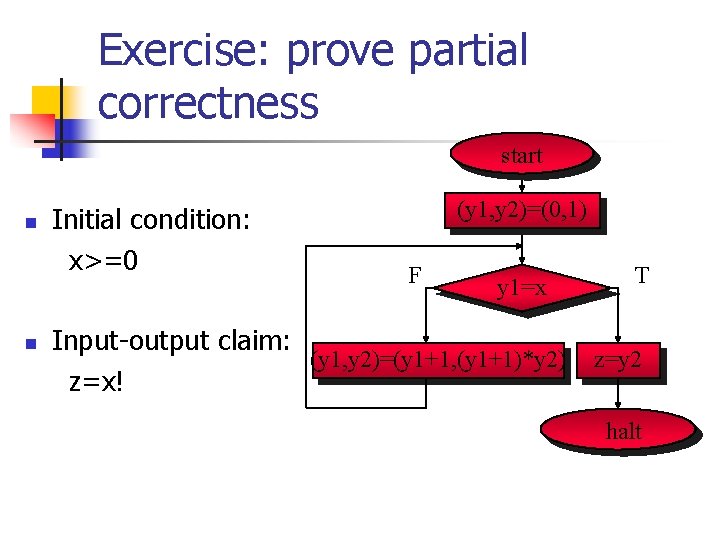
Exercise: prove partial correctness start n n Initial condition: x>=0 (y 1, y 2)=(0, 1) F y 1=x T Input-output claim: (y 1, y 2)=(y 1+1, (y 1+1)*y 2) z=y 2 z=x! halt

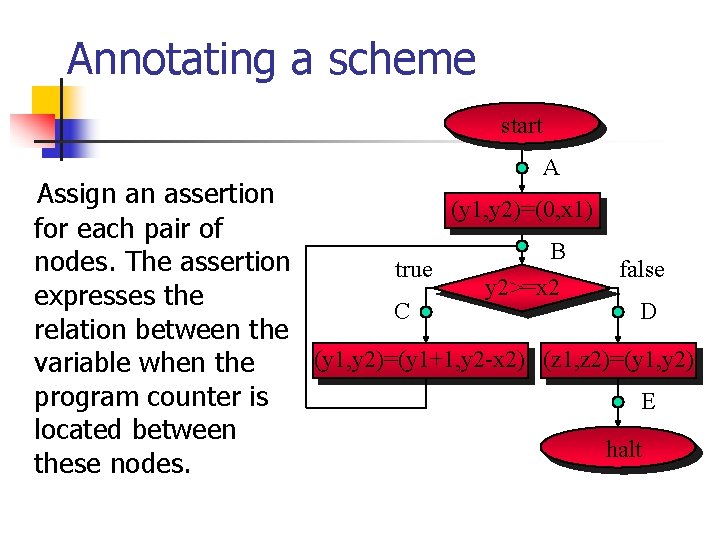
Annotating a scheme start A Assign an assertion (y 1, y 2)=(0, x 1) for each pair of B nodes. The assertion true false y 2>=x 2 expresses the C D relation between the (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) variable when the program counter is E located between halt these nodes.

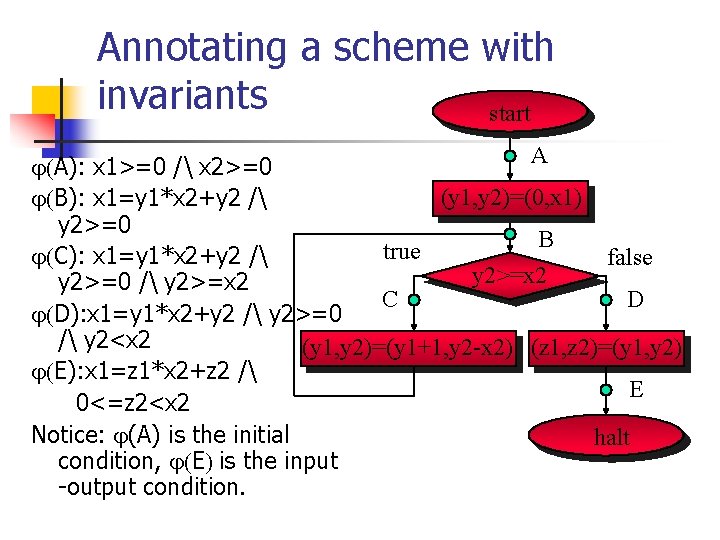
Annotating a scheme with invariants start A A): x 1>=0 / x 2>=0 (y 1, y 2)=(0, x 1) B): x 1=y 1*x 2+y 2 / y 2>=0 B true C): x 1=y 1*x 2+y 2 / false y 2>=x 2 y 2>=0 / y 2>=x 2 C D D): x 1=y 1*x 2+y 2 / y 2>=0 / y 2<x 2 (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) E): x 1=z 1*x 2+z 2 / E 0<=z 2<x 2 Notice: (A) is the initial halt condition, E is the input -output condition.

Verification conditions: assignment A) B) [Yg(X, Y)] A (y 1, y 2)=(0, x 1) Y=g(X, Y) A): x 1>=0 / x 2>=0 B): x 1=y 1*x 2+y 2 / y 2>=0 B) [Yg(X, Y)] = x 1=0*x 2+x 1 / x 1>=0 B A (y 1, y 2)=(0, x 1) B

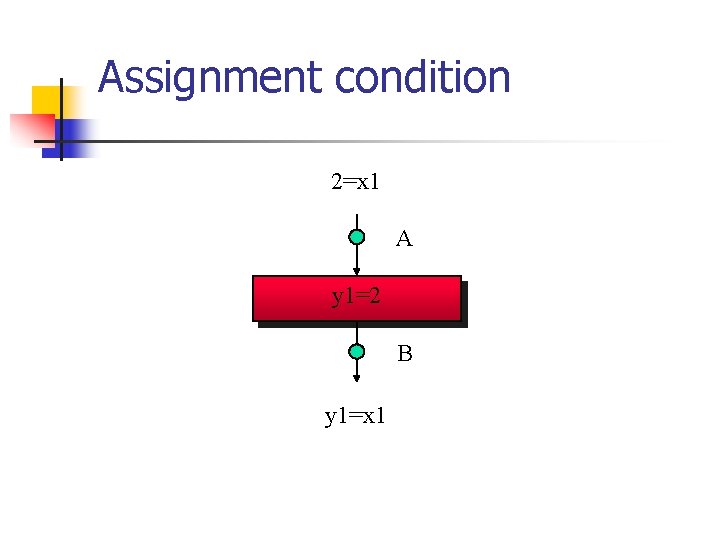
Assignment condition 2=x 1 A (y 1, y 2)=(0, x 1) y 1=2 B y 1=x 1

Another way to understand condition Use two versions of variables: before assignment and after. E. g. , y 1 and y 1’, respectively. postcondition: y 1’=x 1 assignment: y 1’=2 precondition: 2=x 1 A (y 1, y 2)=(0, x 1) y 1=2 B y 1=x 1

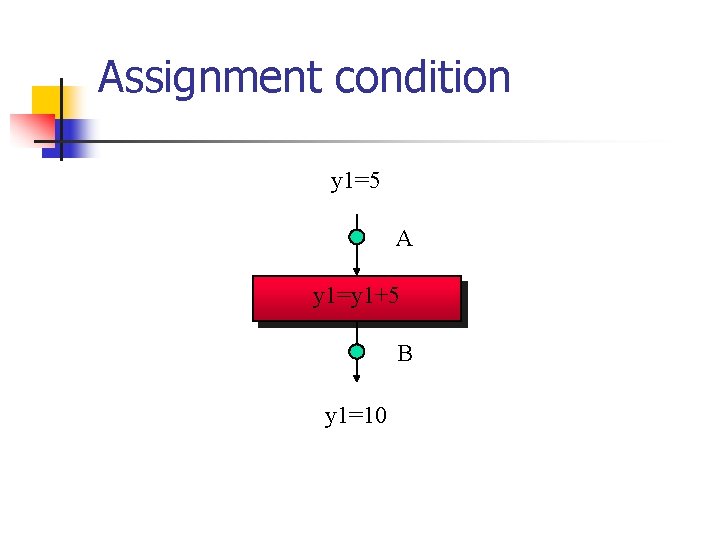
Assignment condition y 1=5 A (y 1, y 2)=(0, x 1) y 1=y 1+5 B y 1=10

Assignment condition Postcondition: y 1’=10 y 1=5 A Assignment: y 1’=y 1+5 Precondition: y 1+5=10, I. e. , y 1=5 (y 1, y 2)=(0, x 1) y 1=y 1+5 B y 1=10

Verification conditions: assignment B): x 1=y 1’*x 2+y 2’ / y 2’ >=0 A): x 1>=0 / x 2>=0 A Assignment: y 1’=0 / y 2’=x 1 B) [Yg(X, Y)] = x 1=0*x 2+x 1 / x 1>=0 (or simply x 1>=0) (y 1, y 2)=(0, x 1) B

Second assignment Precondition: B): x 1=y 1*x 2+y 2 / y 2>=0 Assignment: y 1’=y 1+1/y 2’=y 2 -x 2 Postcondition: B)[Yg(X, Y)]: x 1=(y 1+1)*x 2+y 2 -x 2 / y 2 -x 2>=0 C (y 1, y 2)=(y 1+1, y 2 -x 2) B

Second assignment C): x 1=y 1*x 2+y 2 / y 2>=0 / y 2>=x 2 B): x 1=y 1*x 2+y 2 / y 2>=0 B)[Yg(X, Y)]: x 1=(y 1+1)*x 2+y 2 -x 2 / y 2 -x 2>=0 C (y 1, y 2)=(y 1+1, y 2 -x 2) B

Third assignment D): x 1=y 1*x 2+y 2 / y 2>=0 / y 2<x 2 D (z 1, z 2)=(y 1, y 2) E): x 1=z 1*x 2+z 2 / 0<=z 2<x 2 E)[Zg(X, Y]: x 1=y 1*x 2+y 2 / 0<=y 2<x 2 E

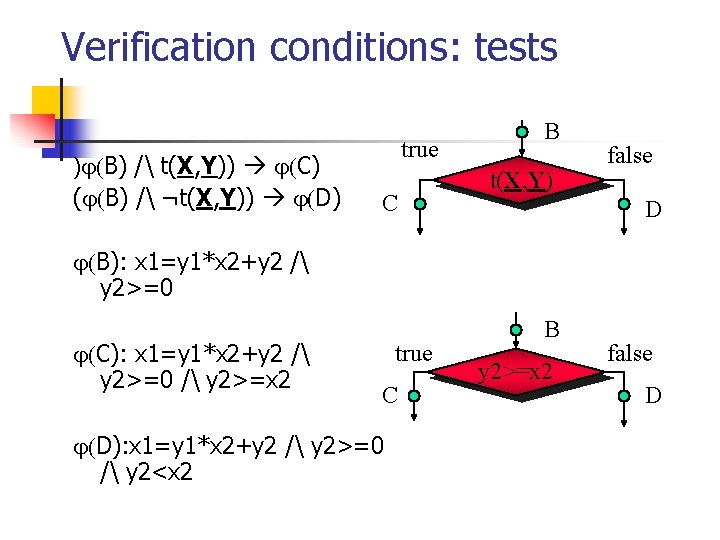
Verification conditions: tests ) B) / t(X, Y)) C) ( B) / ¬t(X, Y)) D) true C B t(X, Y) false D B): x 1=y 1*x 2+y 2 / y 2>=0 C): x 1=y 1*x 2+y 2 / y 2>=0 / y 2>=x 2 true C D): x 1=y 1*x 2+y 2 / y 2>=0 / y 2<x 2 B y 2>=x 2 false D

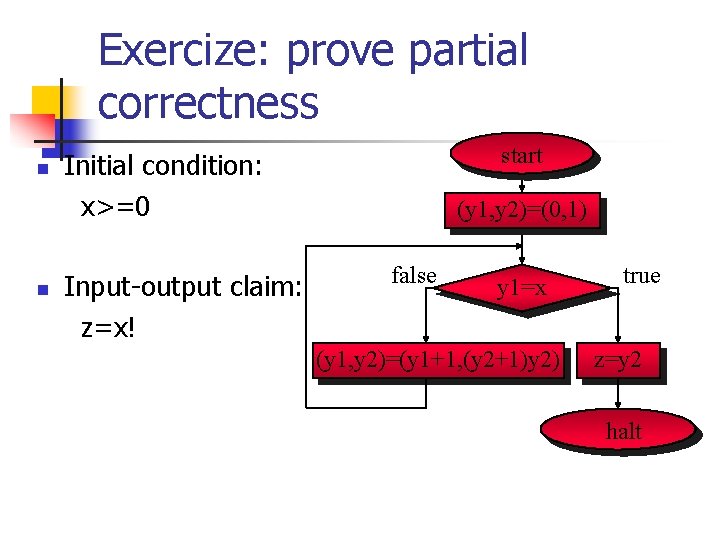
Exercize: prove partial correctness n n start Initial condition: x>=0 Input-output claim: z=x! (y 1, y 2)=(0, 1) false y 1=x (y 1, y 2)=(y 1+1, (y 2+1)y 2) true z=y 2 halt

What have we achieved? n n n For each statement S that appears between points X and Y we showed that if the control is in X when (X) holds and S is executed, then (Y) holds. Initially, we know that (A) holds. The above two conditions can be combined into an induction on the number of statements that were executed: n If after n steps we are at point X, then (X) holds.

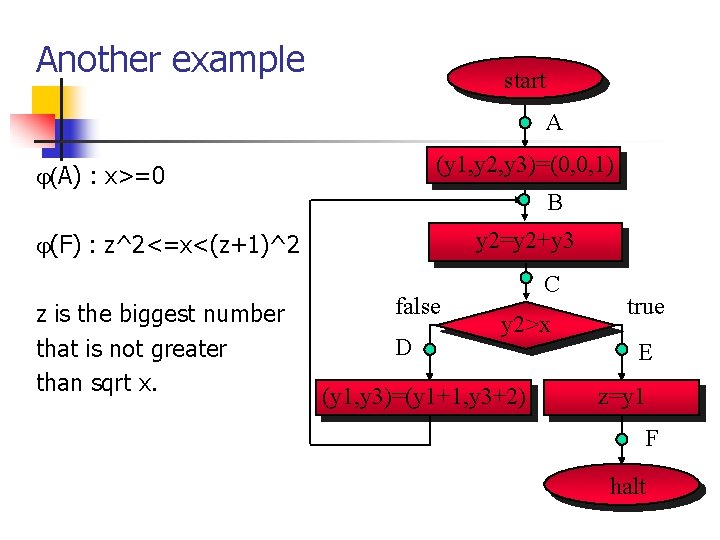
Another example start A (y 1, y 2, y 3)=(0, 0, 1) (A) : x>=0 B y 2=y 2+y 3 (F) : z^2<=x<(z+1)^2 z is the biggest number that is not greater than sqrt x. false D C y 2>x (y 1, y 3)=(y 1+1, y 3+2) true E z=y 1 F halt

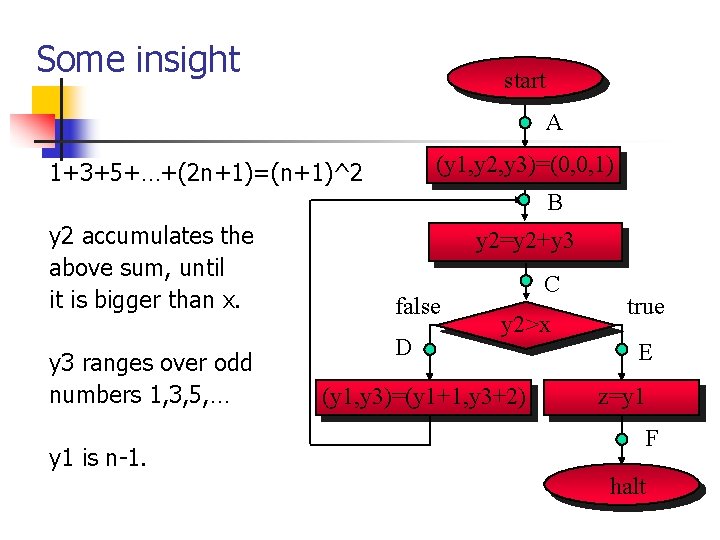
Some insight start A (y 1, y 2, y 3)=(0, 0, 1) 1+3+5+…+(2 n+1)=(n+1)^2 B y 2 accumulates the above sum, until it is bigger than x. y 3 ranges over odd numbers 1, 3, 5, … y 1 is n-1. y 2=y 2+y 3 false D C y 2>x (y 1, y 3)=(y 1+1, y 3+2) true E z=y 1 F halt

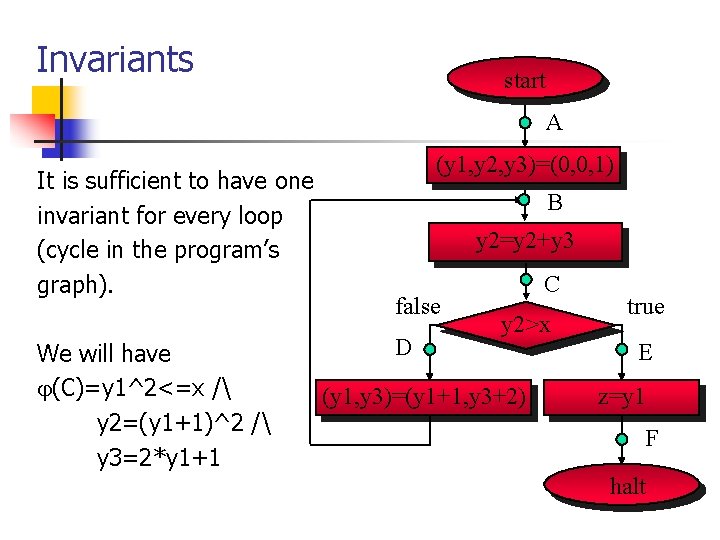
Invariants start A It is sufficient to have one invariant for every loop (cycle in the program’s graph). We will have (C)=y 1^2<=x / y 2=(y 1+1)^2 / y 3=2*y 1+1 (y 1, y 2, y 3)=(0, 0, 1) B y 2=y 2+y 3 false D C y 2>x (y 1, y 3)=(y 1+1, y 3+2) true E z=y 1 F halt

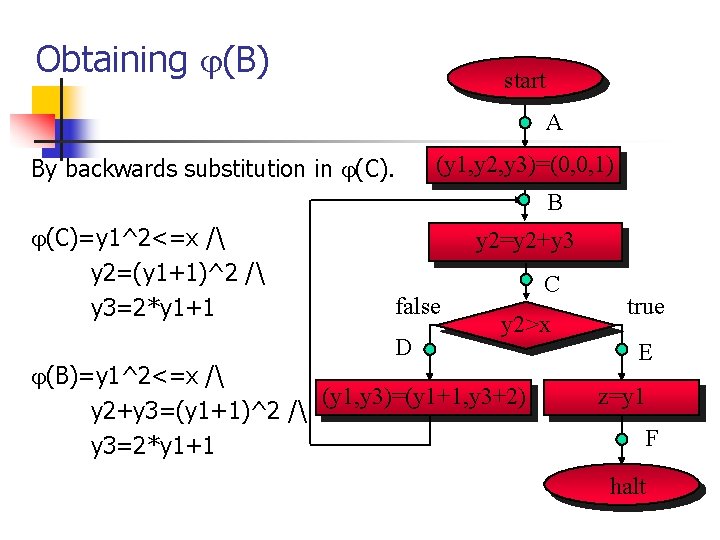
Obtaining (B) start A By backwards substitution in (C). (y 1, y 2, y 3)=(0, 0, 1) B (C)=y 1^2<=x / y 2=(y 1+1)^2 / y 3=2*y 1+1 y 2=y 2+y 3 false D C y 2>x (B)=y 1^2<=x / (y 1, y 3)=(y 1+1, y 3+2) y 2+y 3=(y 1+1)^2 / y 3=2*y 1+1 true E z=y 1 F halt

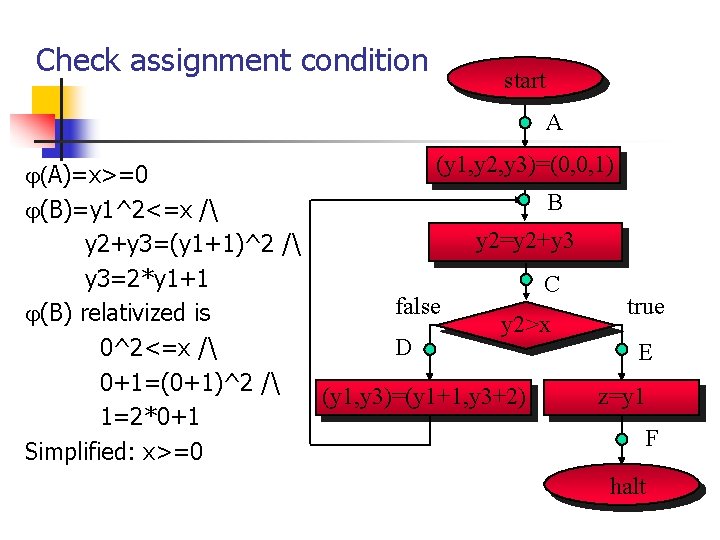
Check assignment condition start A (y 1, y 2, y 3)=(0, 0, 1) (A)=x>=0 B (B)=y 1^2<=x / y 2=y 2+y 3=(y 1+1)^2 / y 3=2*y 1+1 C false true (B) relativized is y 2>x D 0^2<=x / E 0+1=(0+1)^2 / (y 1, y 3)=(y 1+1, y 3+2) z=y 1 1=2*0+1 F Simplified: x>=0 halt

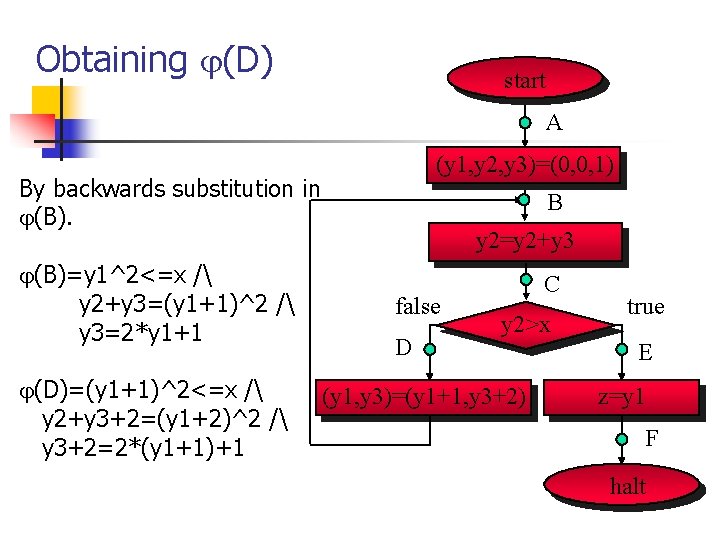
Obtaining (D) start A (y 1, y 2, y 3)=(0, 0, 1) By backwards substitution in (B)=y 1^2<=x / y 2+y 3=(y 1+1)^2 / y 3=2*y 1+1 (D)=(y 1+1)^2<=x / y 2+y 3+2=(y 1+2)^2 / y 3+2=2*(y 1+1)+1 B y 2=y 2+y 3 false D C y 2>x (y 1, y 3)=(y 1+1, y 3+2) true E z=y 1 F halt

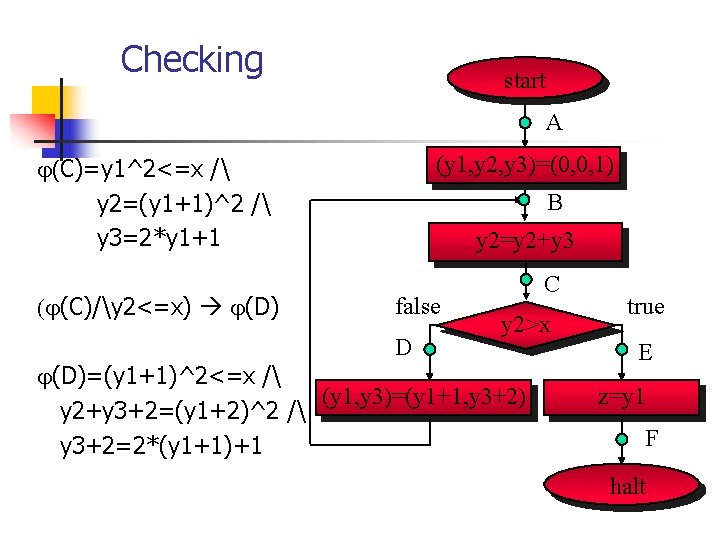
Checking start A (y 1, y 2, y 3)=(0, 0, 1) (C)=y 1^2<=x / y 2=(y 1+1)^2 / y 3=2*y 1+1 (C)/y 2<=x) (D) B y 2=y 2+y 3 false D C y 2>x (D)=(y 1+1)^2<=x / (y 1, y 3)=(y 1+1, y 3+2) y 2+y 3+2=(y 1+2)^2 / y 3+2=2*(y 1+1)+1 true E z=y 1 F halt

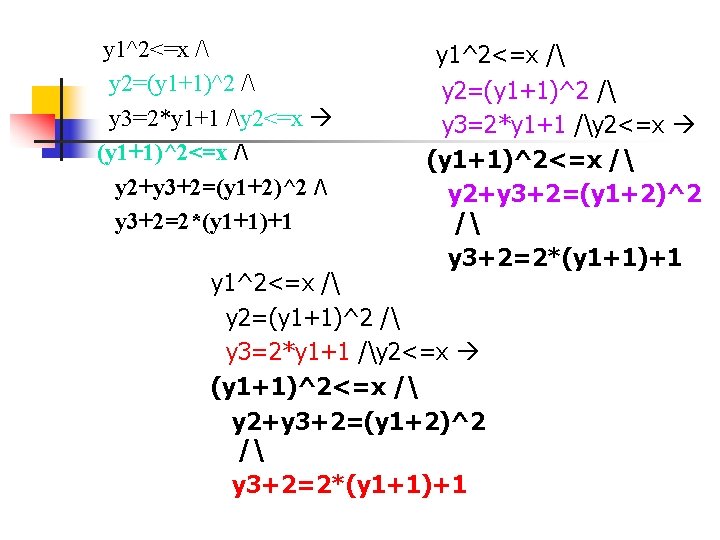
y 1^2<=x / y 2=(y 1+1)^2 / y 3=2*y 1+1 /y 2<=x (y 1+1)^2<=x / y 2+y 3+2=(y 1+2)^2 / y 3+2=2*(y 1+1)+1

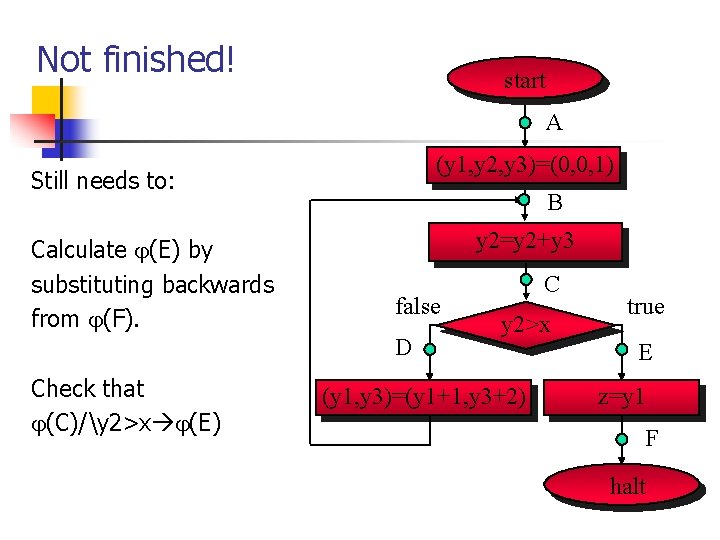
Not finished! start A (y 1, y 2, y 3)=(0, 0, 1) Still needs to: Calculate (E) by substituting backwards from (F). B y 2=y 2+y 3 false D Check that (C)/y 2>x (E) C y 2>x (y 1, y 3)=(y 1+1, y 3+2) true E z=y 1 F halt

Proving termination

Well-founded sets n n Partially ordered set (W, <): n If a<b and b<c then a<c (transitivity). n If a<b then not b<a (asymmetry). n Not a<a (irreflexivity). Well-founded set (W, <): n Partially ordered. n No infinite decreasing chain a 1>a 2>a 3>…

Examples for well founded sets n n Natural numbers with the bigger than relation. Finite sets with the set inclusion relation. Strings with the substring relation. Tuples with alphabetic order: n n (a 1, b 1)>(a 2, b 2) iff a 1>a 2 or [a 1=a 2 and b 1>b 2]. (a 1, b 1, c 1)>(a 2, b 2, c 2) iff a 1>a 2 or [a 1=a 2 and b 1>b 2] or [a 1=a 2 and b 1=b 2 and c 1>c 2].

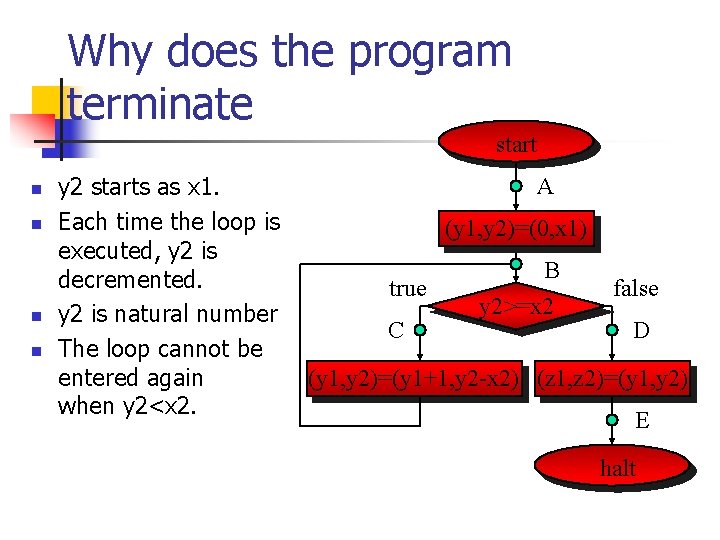
Why does the program terminate start n n y 2 starts as x 1. Each time the loop is executed, y 2 is decremented. y 2 is natural number The loop cannot be entered again when y 2<x 2. A (y 1, y 2)=(0, x 1) true C B y 2>=x 2 false D (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) E halt

Proving termination n n Choose a well-founded set (W, <). Attach a function u(N) to each point N. Annotate the flowchart with invariants, and prove their consistency conditions. Prove that (N) (u(N) in W).

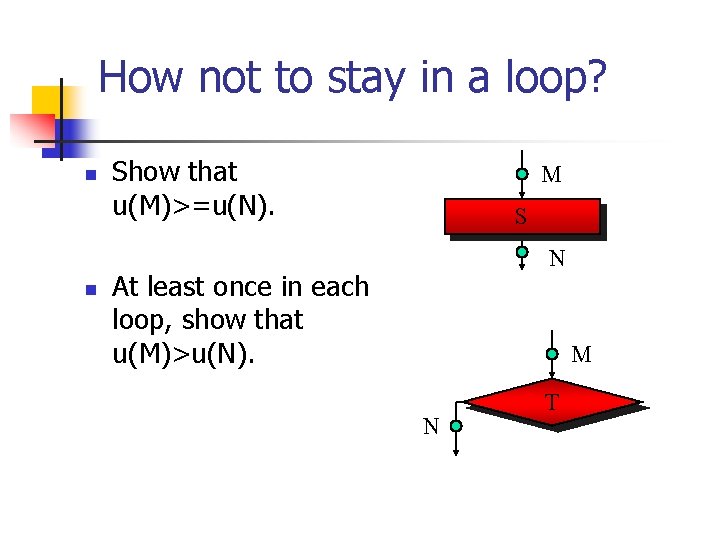
How not to stay in a loop? n n Show that u(M)>=u(N). M S N At least once in each loop, show that u(M)>u(N). M N T

How not to stay in a loop? M For stmt: (M) (u(M)>=u(N)’rel) n stmt N For test (true side): ( (M)/test) (u(M)>=u(N)) n For test (false side): ( (M)/¬test) (u(M)>=u(L)) n M true false test N L

What did we achieve? n n There are finitely many control points. The value of the function u cannot increase. If we return to the same control point, the value of u must decrease (its a loop!). The value of u can decrease only a finite number of times.

Why does the program terminate start u(A)=x 1 u(B)=y 2 u(C)=y 2 u(D)=y 2 u(E)=z 2 A (y 1, y 2)=(0, x 1) true C B y 2>=x 2 false D (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) W: naturals > : greater than E halt

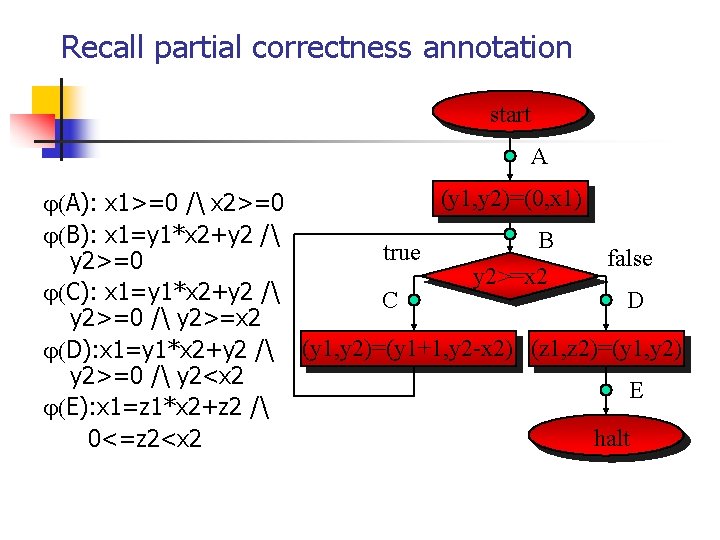
Recall partial correctness annotation start A (y 1, y 2)=(0, x 1) A): x 1>=0 / x 2>=0 B): x 1=y 1*x 2+y 2 / B true false y 2>=0 y 2>=x 2 C): x 1=y 1*x 2+y 2 / C D y 2>=0 / y 2>=x 2 D): x 1=y 1*x 2+y 2 / (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) y 2>=0 / y 2<x 2 E E): x 1=z 1*x 2+z 2 / halt 0<=z 2<x 2

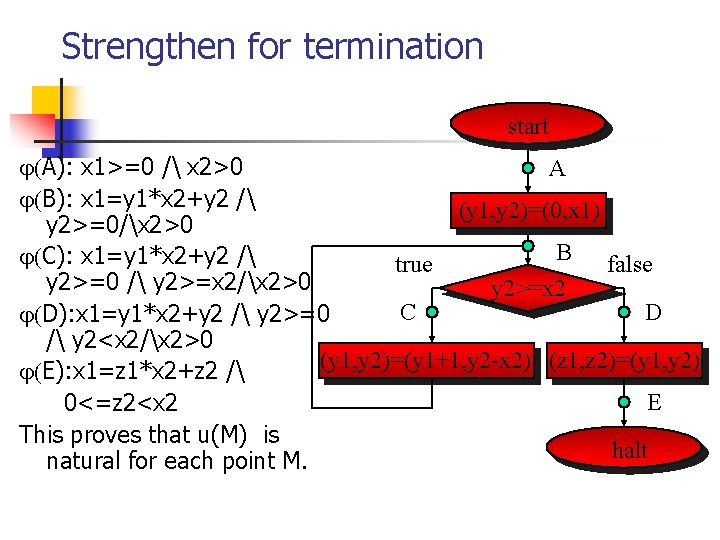
Strengthen for termination start A): x 1>=0 / x 2>0 A B): x 1=y 1*x 2+y 2 / (y 1, y 2)=(0, x 1) y 2>=0/x 2>0 B false C): x 1=y 1*x 2+y 2 / true y 2>=0 / y 2>=x 2/x 2>0 y 2>=x 2 C D D): x 1=y 1*x 2+y 2 / y 2>=0 / y 2<x 2/x 2>0 (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) E): x 1=z 1*x 2+z 2 / E 0<=z 2<x 2 This proves that u(M) is halt natural for each point M.

We shall show: u(A)=x 1 u(B)=y 2 u(C)=y 2 u(D)=y 2 u(E)=z 2 u(A)>=u(B)>=u(C)>u(B)>=u(D)>=u(E) start A (y 1, y 2)=(0, x 1) true C B y 2>=x 2 false D (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) E halt

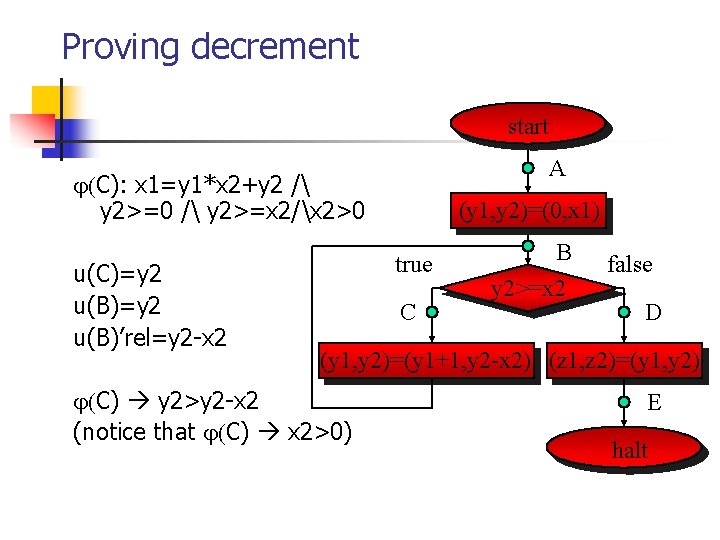
Proving decrement start A C): x 1=y 1*x 2+y 2 / y 2>=0 / y 2>=x 2/x 2>0 u(C)=y 2 u(B)’rel=y 2 -x 2 (y 1, y 2)=(0, x 1) true C B y 2>=x 2 false D (y 1, y 2)=(y 1+1, y 2 -x 2) (z 1, z 2)=(y 1, y 2) C) y 2>y 2 -x 2 (notice that C) x 2>0) E halt

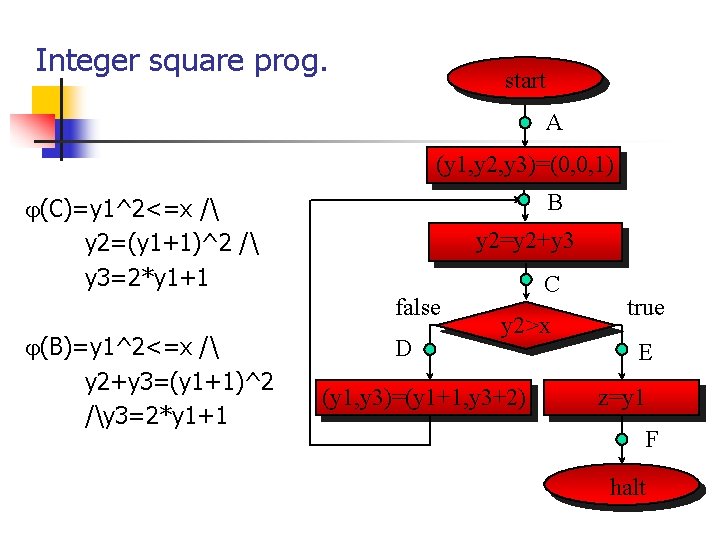
Integer square prog. start A (y 1, y 2, y 3)=(0, 0, 1) B (C)=y 1^2<=x / y 2=(y 1+1)^2 / y 3=2*y 1+1 y 2=y 2+y 3 false (B)=y 1^2<=x / y 2+y 3=(y 1+1)^2 /y 3=2*y 1+1 D C y 2>x (y 1, y 3)=(y 1+1, y 3+2) true E z=y 1 F halt

u(A)=x+1 u(B)=x-y 2+1 u(C)=max(0, x-y 2) u(D)=x-y 2+1 u(E)=u(F)=0 u(A)>=u(B)>u(C)>=u(D)>=u(B) Need some invariants, i. e. , y 2<=x/y 3>0 at points B and D, and y 3>0 at point C. start A (y 1, y 2, y 3)=(0, 0, 1) B y 2=y 2+y 3 false D C y 2>x (y 1, y 3)=(y 1+1, y 3+2) true E z=y 1 F halt