Program Studi Statistika Universitas Brawijaya DETERMINISTIC DYNAMIC PROGRAMMING

� Dynamic programming problems adalah masalah multi tahap(multistage) dimana keputusan dibuat secara berurutan (in sequence) � Beberapa aplikasi dari dynamic programming antara lain: � Network � Resource allocation � Inventory control,

NETWORK PROBLEM Untuk menemukan shortest (longest) path yang menghubungkan dua titik dalam network � Contoh: Joe tinggal di new York dan akan pergi ke LA. Dia berencana menginap di rumah temannya dalam perjalanan tersebut. Joe punya teman di Columbus, Nashville, Louisville, Kansas, Omaha, Dallas, San Antonio, dan Denver. Joe tahu setelah satu hari perjalanan dia akan mencapai Columbus, Nashville atau Louisville. Setelah perjalanan 2 hari akan mencapai Kansas, Omaha, atau Dallas. Setelah 3 hari perjalanan akan mencapai Denver atau San Antonio. Setelah 4 hari akan mencapai LA. Untuk meminimalkan jarak, kemana Joe harus menginap setiap malam dalam perjalanannya ? �

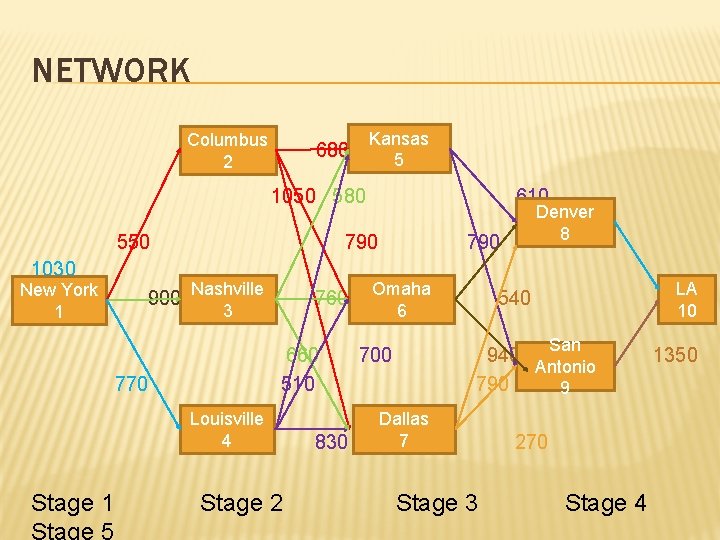
NETWORK Columbus 2 Kansas 5 680 1050 580 550 1030 New York 1 790 900 Nashville 760 3 660 510 770 Louisville 4 Stage 1 610 Stage 2 830 Denver 8 790 Omaha 6 LA 10 540 San 700 940 Antonio 790 9 Dallas 7 Stage 3 270 Stage 4 1350

THE RECURSION Ide bekerja secara backward adalah kita mulai menyelesaikan masalah dari yang paling sederhana untuk menyelesaikan masalah yang kompleks. Jadi kita mulai dari kota yang hanya membutuhkan perjalanan satu hari ke LA yaitu kota Denver dan San Antonio (kota pada stage 4) Kemudian kita gunakan informasi dari stage 4 untuk menemukan jarak terpendek dari kota pada stage 3 ( yang membutuhkan 2 hari) ke LA Demikian seterusnya sampai kita menemukan shortest path dari kota New York ke LA

SOLUSI � Tentukan Cij = jarak kota i ke kota j � Tentukan Ft(i) = panjang shortest path dari kota i ke kota LA dimana kota i adalah kota pada stage t � Tentukan shortest path ke LA dari setiap kota di setiap stage mulai dari stage akhir

STAGE 4 COMPUTATION Karena hanya ada satu path dari kota pada stage 4 ke LA maka kita dapat langsung menentukan Jarak terpendek dari kota Denver ke kota LA adalah F 4(8) = 1030 Dari kota San Antonio ke LA adalah F 4(9) = 1390

STAGE 3 COMPUTATION � Terdapat tiga kota pada stage 3 yaitu kota Kansas, Omaha dan Dallas � Dari kota Kansas terdapat 2 path menuju kota LA yaitu Path 1. Kansas – Denver – kemudian mengambil shortest path dari Denver ke LA Path 2. Kansas – San Antonio – kemudian mengambil shortest path dari San Antonio ke LA

STAGE 2 COMPUTATION Pada stage 2 terdapat 3 kota yaitu Columbus, Nashville, dan Louisville Terdapat 3 path dari Coulumbus ke LA yaitu Path 1. Columbus – Kansas – kemudain mengambil shortest path dari Kansas Path 2. Columbus – Omaha – kemudian mengambil shortest path dari Omaha Path 3. Columbus – Dallas – kemudian mengambil shortest path dari Dallas

STAGE 1 COMPUTATION � Dari kota 1(New York) terdapat 3 Path ke kota LA yaitu Path 1. New York – Columbus – kemudian mengikuti shortest path dari Columbus Path 2. new York – Nashville – kemudian mengikuti shortest pat dari Nashville Path 3. New York – Louisville – kemudian mengikuti shortest path dari Louisville

KARAKTERISTIK APLIKASI DYNAMIC PROGRAMMING � Karakteristik 1 � Problem dapat dibagi menjadi beberapa stage dan dibutuhkan sebuah keputusan pada setiap stage. � Karakteristik � Setiap 2 stage memiliki beberapa state. � state, adalah informasi yang dibutuhkan pada setiap stage untuk membuat keputusan optimal. � Karakteristik � Keputusan 3 yang dipilih pada setiap stage menggambarkan bagaimana state pada stage sekarang ditransformasi ke state pada stage berikutnya.

� Karakteristik 4 � Diberikan state sekarang, keputusan optimal untuk setiap stage yang tersisa harus tidak tergantung pada state yang dicapai sebelumnya atau keputusan yang diambil sebelumnya. � Ide ini dikenal sebagai the principle of optimality. � Karakteristik � Jika 5 state untuk suatu problem telah diklasifikasikan ke T stage, harus terdapat rekursi yang menghubungkan biaya atau reward yang didapat selama stage t, t+1, …. , T terhadap biaya atau reward yang didapat dari stages t+1, t+2, …. T.

PRODUCTION AND INVENTORY PROBLEM � Dynamic programming dapat digunakan untuk menyelesaikan masalah inventory dengan karakteristik berikut: 1. 2. Waktu dibagi menjadi beberapa periode. Periode sekarang adalah periode 1, berikutnya periode 2 dan terakhir adalah periode T. Pada awal periode 1, permintaan selama setiap periode diketahui. Pada awal setiap periode, perusahaan harus menentukan berapa banyak unit yang harus diproduksi. Kapasitas produksi selama setiap periode terbatas.

3. 4. 5. Permintaan pada setiap periode harus dipenuhi tepat waktu dari inventory ataau produksi sekarang. Selama setiap periode dimana dilakukan produksi maka akan timbul fixed cost dan variabel cost. Perusahaan memiliki kapasitas penyimpanan yang terbatas. Hal ini mencerminkan batas pada end-ofperiod inventory. Holding cost per unit timbul pada setiap period’s ending inventory. Tujuan perusahaan adalah menentukan jadwal produksi untuk meminimumkan total cost dari pemenuhan permintaan tepat waktu untuk periode 1, 2, …. , T.

� Pada model ini, posisi inventory perusahaan direview pada akhir setiap periode dan kemudian keputusan produksi dibuat. � Model seperti ini dinamakan periodic review model. � Model ini berlawanan dengan the continuous review model dimana perusahaan mengetahui posisi inventory setiap saat dan memesan order atau memulai produksi setiap saat.

PRODUCTION AND INVENTORY PROBLEMS � MJ berencana memproduksi 15 mobil selama 5 bulan yaitu bulan Mei, Juni, Juli, Agustus dan September. 21

DATA � � � Maximum level produksi adalah 3 untuk Juli, dan 4 untuk setiap bulan yang lain. Kapasitas penyimpanan adalah 2 mobil dengan holding cost adalah $2, 500 per bulan ($3, 000 untuk Mei). Fixed costs (untuk asuransi dan lain – lain) hanya terjadi jika mobil benar – benar diproduksi 22

TUJUAN DARI MJ Membuat jadwal produksi yang meminimumkan total cost 23

MJ - DEFINISI � Stage variable j: Bulan ke - j. � State variable Xj: Banyaknya mobil di inventory pada awal bulan ke - j � Decision variable Dj: Jumlah produksi untuk bulan ke – j 24

MJ - DEFINISI � Stage cost function: � Fixed costs FCj(Dj) terjadi jika dalam bulan ke j terdapat produksi mobil. Sehingga FCj(Dj) = Sj FCj(0) = 0 jika Dj > 0 jika Dj = 0 • Production costs PCj(Dj) dalam bulan j proporsional dengan jumlah mobil yang diproduksi PCj(Dj) = Pj. Dj • Holding (storage) costs HCj(Dj) dalam bulan ke j dibayarkan untuk mobil yang tidak terjual di akhir bulan ke j. Untuk bulan j =1: HC 1(D 1) = 3000(X 1 + D 1 - C 1)= 3000 D 1 – 9000 Untuk bulan j = 2, 3, 4, 5: HCj(Dj ) =2500(Xj+Dj - Cj) Asumsi: X 1 = 0 dan C 1 = 3 25

MJ - DEFINISI � � � The optimal value function Fj(Xj) dalam bulan j adalah minimum total cost yang terjadi dari bulan ke j sampai 5( September), jika terdapat Xj mobil pada inventory di awal bulan ke-j Boundary conditions F 5(X 5): F 5(0) = 2, 000 + 23, 000(4) = $94, 000; D 5 = 4 F 5(1) = 2, 000 + 23, 000(3) = $71, 000; D 5 = 3 F 5(2) = 2, 000 + 23, 000(2) = $48, 000; D 5 = 2 Optimal solution F 1(0) adalah minimum total cost dari bulan Mei sampai September jika tidak ada inventory awal 26

THE RECURSION Fj(Xj) = Min{FCj(Dj) + PCj(Dj) + HCj(Dj) + Fj+1(Xj +Dj - Cj)}, Pada semua Dj yang feasible. Dj feasible hanya jika memenuhi kondisi berikut : Dj + X j ³ C j ; D 3 £ 3 for July; Dj £ 4 for j = 1, 2, 4, 5; Dj + Xj - Cj £ 2; Dj ³ 0 27

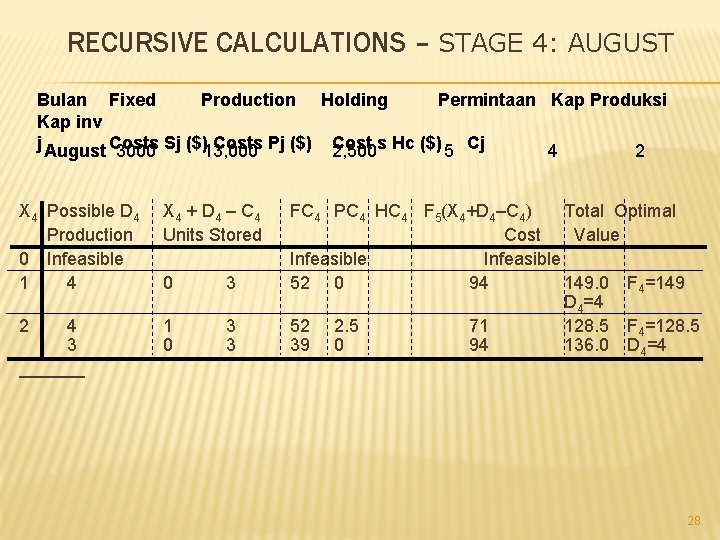
RECURSIVE CALCULATIONS – STAGE 4: AUGUST Bulan Fixed Production Holding Permintaan Kap Produksi Kap inv j August Costs Pj ($) Cost 3000 Sj ($)13, 000 2, 500 s Hc ($) 5 Cj 4 2 X 4 Possible D 4 Production 0 Infeasible 1 4 X 4 + D 4 – C 4 Units Stored 0 3 2 1 0 3 3 4 3 FC 4 PC 4 HC 4 F 5(X 4+D 4–C 4) Total Optimal Cost Value Infeasible 52 0 94 149. 0 F 4=149 D 4=4 52 2. 5 71 128. 5 F 4=128. 5 39 0 94 136. 0 D 4=4 28

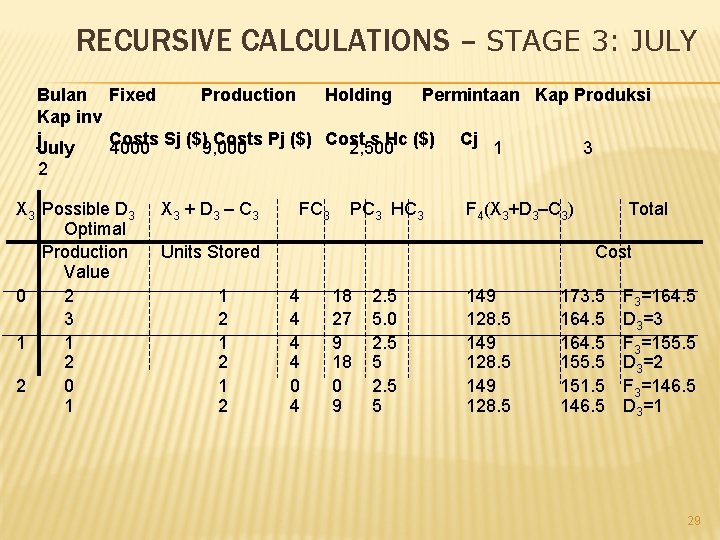
RECURSIVE CALCULATIONS – STAGE 3: JULY Bulan Fixed Production Holding Permintaan Kap Produksi Kap inv j. July Costs Pj ($) Cost s Hc ($) Cj 1 4000 Sj ($)9, 000 2, 500 3 2 X 3 Possible D 3 Optimal Production Value 0 2 3 1 1 2 2 0 1 X 3 + D 3 – C 3 FC 3 PC 3 HC 3 F 4(X 3+D 3–C 3) Units Stored 1 2 1 2 Total Cost 4 4 0 4 18 27 9 18 0 9 2. 5 5. 0 2. 5 5 149 128. 5 173. 5 164. 5 155. 5 151. 5 146. 5 F 3=164. 5 D 3=3 F 3=155. 5 D 3=2 F 3=146. 5 D 3=1 29

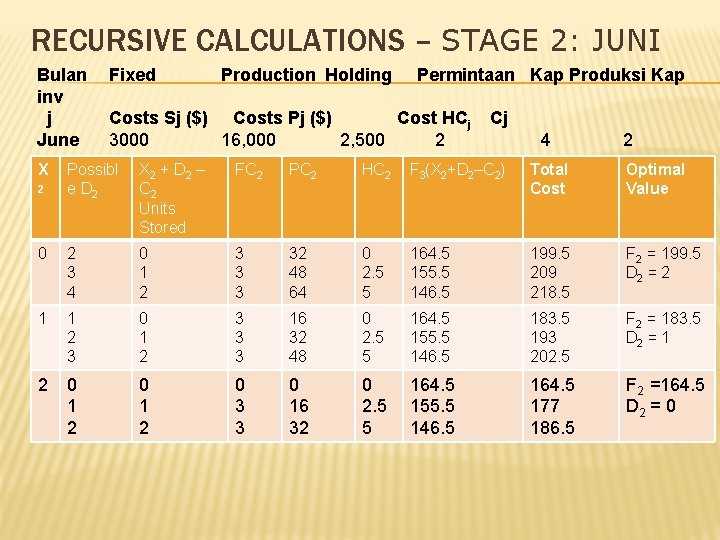
RECURSIVE CALCULATIONS – STAGE 2: JUNI Bulan inv j June X Fixed Production Holding Permintaan Kap Produksi Kap Costs Sj ($) Costs Pj ($) Cost HCj 3000 16, 000 2, 500 2 Cj 4 2 Possibl e D 2 X 2 + D 2 – C 2 Units Stored FC 2 PC 2 HC 2 F 3(X 2+D 2–C 2) Total Cost Optimal Value 0 2 3 4 0 1 2 3 32 48 64 0 2. 5 5 164. 5 155. 5 146. 5 199. 5 209 218. 5 F 2 = 199. 5 D 2 = 2 1 1 2 3 0 1 2 3 3 3 16 32 48 0 2. 5 5 164. 5 155. 5 146. 5 183. 5 193 202. 5 F 2 = 183. 5 D 2 = 1 2 0 3 3 0 16 32 0 2. 5 5 164. 5 155. 5 146. 5 164. 5 177 186. 5 F 2 =164. 5 D 2 = 0 2

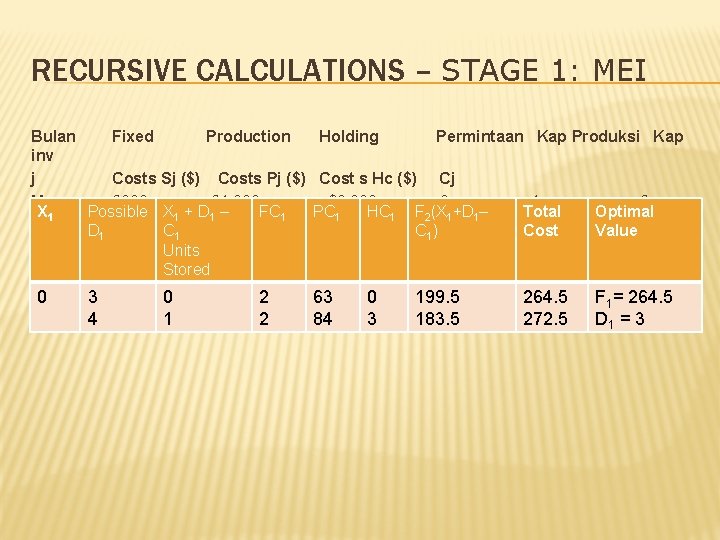
RECURSIVE CALCULATIONS – STAGE 1: MEI Bulan Fixed Production Holding Permintaan Kap Produksi Kap inv j Costs Sj ($) Costs Pj ($) Cost s Hc ($) Cj May 2000 21, 000 $3, 000 3 4 2 X 1 Possible X 1 + D 1 – FC 1 PC 1 HC 1 F 2(X 1+D 1– Total Optimal D 1 C 1 ) Cost Value Units Stored 0 3 4 0 1 2 2 63 84 0 3 199. 5 183. 5 264. 5 272. 5 F 1= 264. 5 D 1 = 3

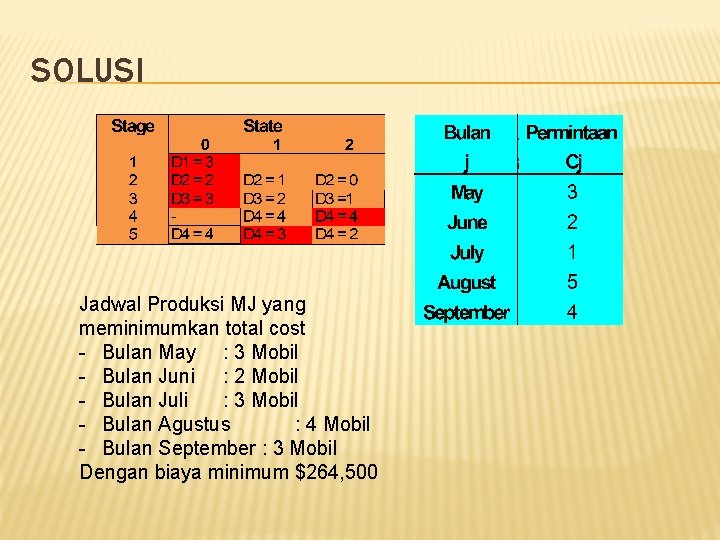
SOLUSI Jadwal Produksi MJ yang meminimumkan total cost - Bulan May : 3 Mobil - Bulan Juni : 2 Mobil - Bulan Juli : 3 Mobil - Bulan Agustus : 4 Mobil - Bulan September : 3 Mobil Dengan biaya minimum $264, 500

RESOURCE ALLOCATION PROBLEM Kementrian tenaga kerja memiliki dana sebesar 5 juta dollar untuk digunakan oleh kementrian – kementrian yang lain untuk menciptakan tenaga kerja � Terdapat 4 kementrian yang mengajukan permohonan dana untuk kepentingan penciptaan tenaga kerja. � Kementrian tenaga kerja ingin mengalokasikan dana untuk memaksimalkan banyaknya tenaga kerja yang diciptakan � 33

� Data Estimasi pekerjaan baru yang tercipta 34

SOLUSI � Kementrian tenaga kerja ingin : � Memaksimumkan total banyaknya tenaga kerja baru � Biaya yang tersedia adalah $5 juta. 35

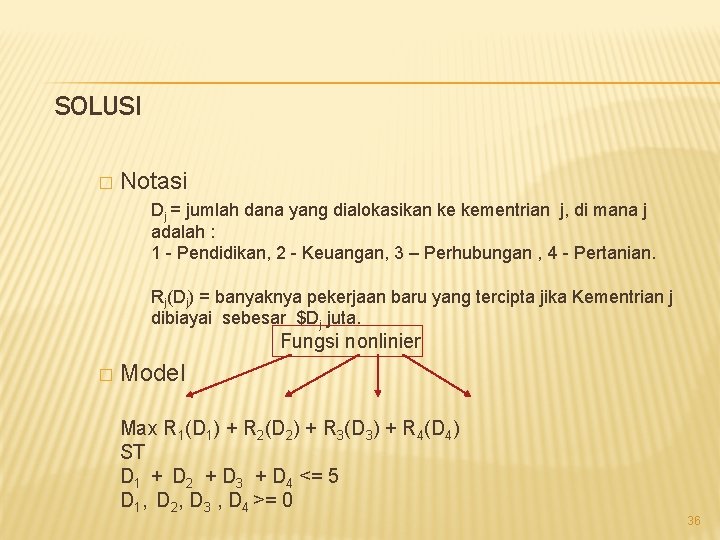
SOLUSI � Notasi Dj = jumlah dana yang dialokasikan ke kementrian j, di mana j adalah : 1 - Pendidikan, 2 - Keuangan, 3 – Perhubungan , 4 - Pertanian. Rj(Dj) = banyaknya pekerjaan baru yang tercipta jika Kementrian j dibiayai sebesar $Dj juta. Fungsi nonlinier � Model Max R 1(D 1) + R 2(D 2) + R 3(D 3) + R 4(D 4) ST D 1 + D 2 + D 3 + D 4 <= 5 D 1, D 2, D 3 , D 4 >= 0 36

THE BACKWARD DYNAMIC PROGRAMMING � Definisikan Fj(Xj) adalah maksimum banyaknya pekerjaan baru yang diciptakan oleh kementrian (stage) j, j+1, …, 4, jika tersedia dana sebesar $Xj juta (state) untuk kementrian j sampai 4. 37

THE BACKWARD DYNAMIC PROGRAMMING � Stage 4: Kementrian Pertanian, (KPt) � � Mulailah dengan tahap terakhir j = 4 (Kementrian Pertanian, KPt). Alokasikan dana yang memaksimalkan jumlah pekerjaan baru yang diciptakan untuk kementrian ini. Jelas, solusi optimal untuk kementrian terakhir adalah menggunakan semua jumlah yang tersedia pada stage ini). Solusi optimal untuk stage terakhir disebut “The boundary condition” 38

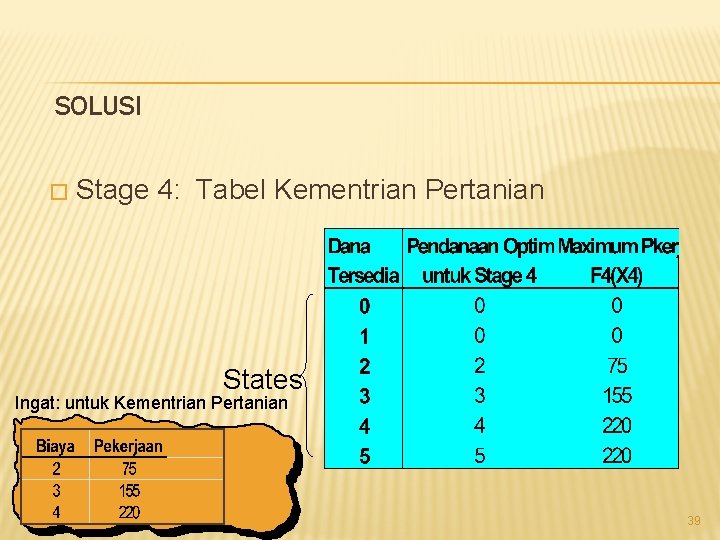
SOLUSI � Stage 4: Tabel Kementrian Pertanian States Ingat: untuk Kementrian Pertanian 39

SOLUSI � Stage 3: Kementrian Perhubungan, (KPh) Pada stage ini kita mempertimbangkan pendanaan untuk Kementrian Perhubungan dan Kementrian Pertanian � Untuk jumlah dana tertentu yang tersedia untuk kedua kementrian ini, keputusan besarnya dana yang diberikan untuk kementrian KPh akan berpengaruh pada dana yang tersedia untuk KPt � 40

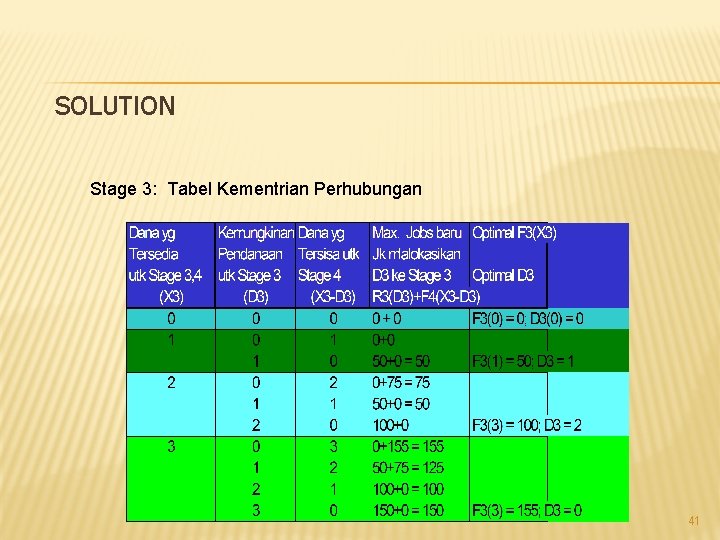
SOLUTION Stage 3: Tabel Kementrian Perhubungan 41

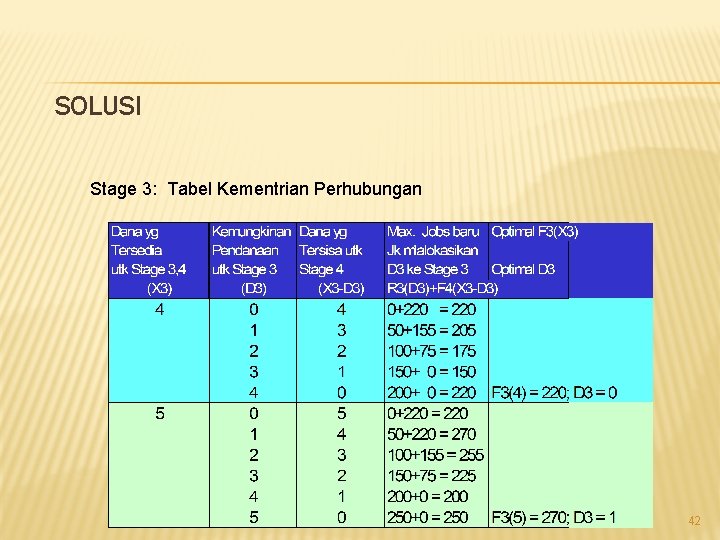
SOLUSI Stage 3: Tabel Kementrian Perhubungan 42

SOLUSI � Stage 2: Kementrian Keuangan, (KKu) � Pada stage ini kita memikirkan pendanaan untuk. Kementrian Keuangan dua Kementrian sebelumnya yaitu Kementrian Perhubngan dan Pertanian � Untuk state tertentu (jumlah dana yang tersedia untuk ketiga Kementrian ), keputusan mengalokasikan sejumlah dana untuk Kementrian Keuangan berpengaruh pada jumlah dana yang tersedia untuk Kementrian Perhubungan dan Pertanian (state pada stage j = 3). 43

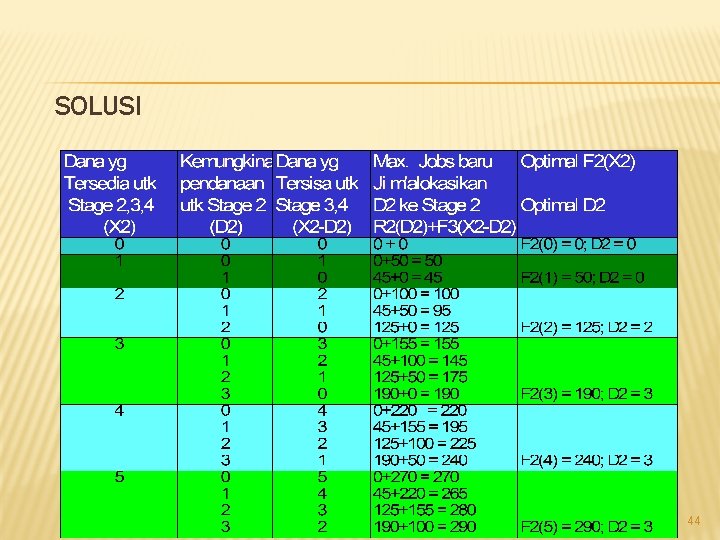
SOLUSI 44

SOLUSI � Stage 1: Kementrian Pendidikan (KPd) Pada stage ini kita memikirkan pendanaan untuk Kementrian Pendidikan dan semua kementrian sebelumnya. � Perhatikan bahwa pada stage 1 masih terdapat $5 juta untuk dialokasikan (X 1 = 5). � 45

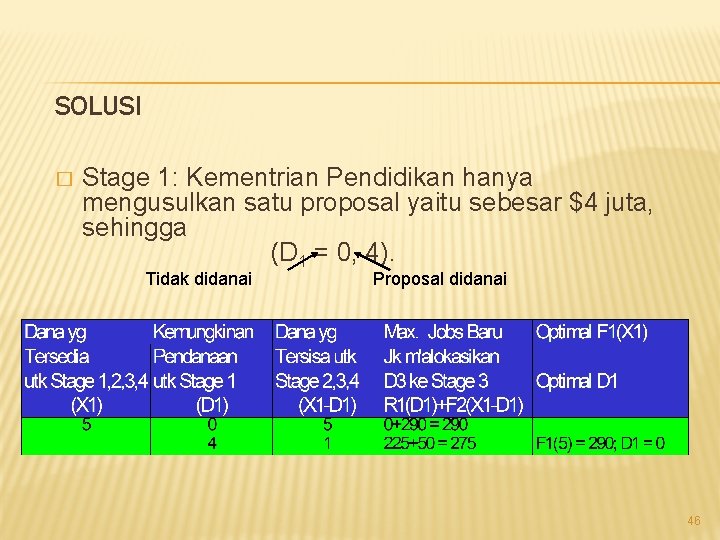
SOLUSI � Stage 1: Kementrian Pendidikan hanya mengusulkan satu proposal yaitu sebesar $4 juta, sehingga (D 1 = 0, 4). Tidak didanai Proposal didanai 46

SOLUSI Alokasi pendanaan optimal untuk memaksimalkan banyaknya pekerjaan yang diciptakan adalah : Pendidikan Keuangan = $0 = $3 million Perhubungan = 47

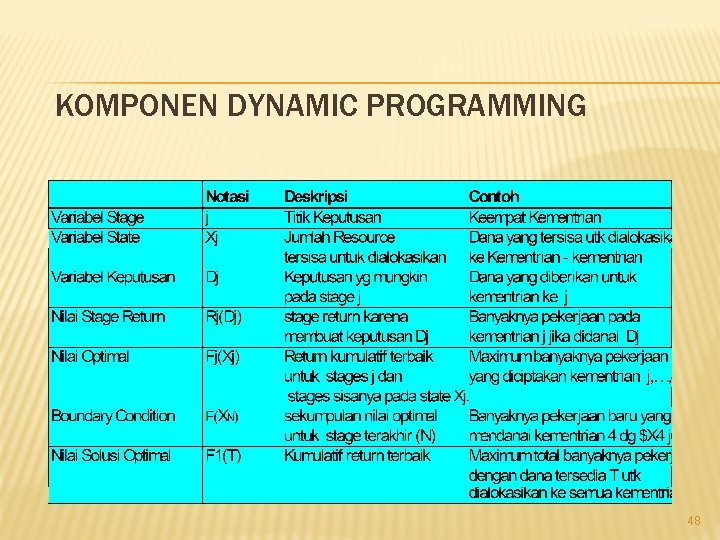
KOMPONEN DYNAMIC PROGRAMMING 48

DYNAMIC RECURSIVE RELATIONSHIP � Dynamic programming adalah proses rekursif � � Recursive relationship berikut menggambarkan proses untuk resource allocation Definisikan Fj(Xj) sebagai maksimum banyaknya pekerjaan baru yang diciptakan oleh kementrian (stage j, j+1, …, 4, jika tersedia $Xj juta untuk pendanaan kementrian (stage) j sampai 4. Fj(Xj) = Max {(Rj(Xj) + Fj+1(Xj - Dj)} Untuk semua Xj yang feasible 49

DYNAMIC RECURSIVE RELATIONSHIP Bentuk dari recursion relation berbeda dari satu problem ke problem yang lain, tapi secara umum idenya sama : Lakukan yang terbaik untuk stage yang tersisa dengan resource sisa yang tersedia. 50

DYNAMIC PROGRAMS AS NETWORKS Jaringan (Networks) dapat digunakan untuk memodelkan multistage decision problems yang diselesaikan dengan dynamic programming approach. � Setiap node merepresentasikan nilai state variable pada setiap stage. � Setiap arc merepresentasikan keputusan yang mungkin pada state tertentu. Stage return adalah nilai (panjang) pada setiap arc. � Tujuannya adalah menemukan path terpanjang(terpendek). � 51

NETWORK PRESENTATIONRESOURCE ALLOCATION PROBLEM 52

FORMULATING DYNAMIC PROGRAMMING RECURSIONS � Pada banyak dynamic programming problems, stage tertentu terdiri atas semua state yang mungkin � Jika kasusnya adalah seperti ini maka dynamic programming recursion dapat dituliskan dalam bentuk berikut: Ft(i) = min{(cost during stage t) + ft+1 (new stage at stage t +1)} dimana minimum pada persamaan di atas adalah untuk semua keputusan yang mungkin (feasible) bila state pada stage t adalah i

� Formulasi yang benar menghasruskan kita mengidentifikasi tiga aspek penting dari masalah tersebut : Aspect 1: Sekumpulan keputusan yang feasible untuk state dan stage tertentu. � Aspect 2: Kita harus menentukan bagaimana biaya selama periode waktu sekarang (stage t) tergantung pada nilai t, state yang sekarang dan keputusan yang dipilih pada stage t. � Aspect 3: Kita harus menentukan bagaimana state pada stage t+1 tergantung pada nilai t, state pada stage t dan keputusan yang diambil pada stage t. � � Tidak semua recursi merupakan bentuk dari yang telah ditunjukkan sebelumnya.

A FISHERY EXAMPLE � Pemilik danau harus memutuskan berapa banyak bass yang harus ditangkap dan dijual setiap tahun. � Jika dia menjual x bass selama tahun t, maka pendapatan r(x) didapatkan. � Biaya menangkap x bass selama setahun adalah fungsi c(x, b) dari banyaknya bass yang ditangkap selama tahun tersebut dan b banyaknya bass di danau pada awal tahun tersebut. Tentu saja bass bereproduksi.

A FISHERY EXAMPLE � Untuk memodelkan masalah ini, kita asumsikan bahwa banyaknya bass didalam danau pada awal tahun adalah 20% lebih banyak dari banyaknya bass yang tersisa didanau pada akhir tahun sebelumnya. � Asumsikan bahwa terdapat 10, 000 bass di danau pada awal tahun pertama. � Bentuklah dynamic programming recursion yang dapat digunakan untuk memaksimumkan net profit pemiliknya selama T- tahun.

A FISHERY EXAMPLE � � Dalam suatu masalah dimana keputusan harus dibuat pada beberapa titik waktu. Seringkali terdapat trade off dari keuntungan sekarang dan keuntungan masa datang. Pada awal tahun T, pemilik danau tidak perlu khawatir tentang efek bahwa penangkapan bass akan berpengaruh pada populasi di danau pada masa datang. Jadi, masalah pada awal tahun T relative lebih mudah diselesaikan. Untuk alasan ini, kita pilih waktu sebagai stage. Pada setiap stage, pemilik danau harus memutuskan berapa banyak bass yang harus ditangkap.

A FISHERY EXAMPLE � Kita tentukan xt adalah banyaknya bass yang ditangkap selama tahun t. � Untuk menentukan nilai optimal dari xt, pemilik danau hanya perlu tahu berapa banyak bass (sebut sebagai bt) di danau pada awal tahun ket. sehinggastate pada awal tahun t adalah bt. � Kita tentukan ft (bt) adalah maximum net profit yang dapat diperoleh dari bass yang ditangkap selama tahun t, t+1, …T jika terdapat bt bass di danau pada awal tahun t.

A FISHERY EXAMPLE � Sekarang � Aspect kita bahas aspek 1 -3 dari rekursi. 1: apakah keputusan yang diijinkan? Selama setiap tahun kita tidak dapat menangkap � Bass lebih banyak dari yang ada di danau. Sehungga, dalam setiap state dan untuk semua t 0 ≤ xt ≤ bt harus terpenuhi. � Aspect 2: berapakah net profit yang didapatkan selama tahun t ? Jika xt bass ditangkap selama satu tahunyang dimulai bt bass di danau, maka net profit adalah r(xt) – c(xt, bt). � Aspect 3: Apakah state selama t+1? State tahun t+1 adalah 1. 2 (bt – xt).

A FISHERY EXAMPLE � Setelah tahun T, tidak ada future profit yang harus dipertimbangkan, sehingga ft(bt)=max{r(xt) – c(xt, bt)+ft+1[1. 2(bt-xt)]} dimana 0 ≤ xt ≤ bt. � Kita gunakan persamaan ini untuk bekerja backward sampai f 1(10, 000) selesai dihitung. � Kemudian untuk menentukan optimal fishing policy, kita pilih x 1 adalah nilai yang mencapai maksimum dalam persamaan untuk f 1(10, 000). � Kemudian tahun 2 akan mulai dengan 1. 2(10, 000 – x 1) bass di danau.

A FISHERY EXAMPLE � Artinya x 2 harus dipilih nilai yang mencapai maximum di persamaan untuk f 2(10, 000 x 1)). � Lanjutkan terus sampai nilai optimal x 3, x 4, …x. T ditentukan.

COMPUTERS AND DYNAMIC PROGRAMMING � Dynamic programming problems biasanya diselesaikan menggunakan program komputer. � Karena dynamic problem berbeda - beda, tidak ada universal code untuk menyelesaikan semua masalah tersebut. 62

DYNAMIC PROGRAMMING - EXAMPLES � Dalam setiap permasalahan dynamic programming kita harus dapat menentukan / mengidentifikasi hal – hal berikut: : � � � � The stage variable. The state variable. The decision variable. The stage return or cost function(s). The optimal value function. The boundary conditions. The optimal solution value (stopping rule). The recurrence relation. 63