Program Perkuliahan Dasar Umum Sekolah Tinggi Teknologi Telkom

Program Perkuliahan Dasar Umum Sekolah Tinggi Teknologi Telkom 0 Barisan dan Deret

Barisan 0 0 Definisi Barisan bilangan didefinisikan sebagai fungsi dengan daerah asal merupakan bilangan asli. Notasi: f: N R n f(n ) = an Fungsi tersebut dikenal sebagai barisan bilangan Riil {an} dengan an adalah suku ke-n. Bentuk penulisan dari barisan : 1. bentuk eksplisit suku ke-n 2. ditulis barisannya sejumlah berhingga suku awalnya. 3. bentuk rekursi 12/5/2020 [MA 1124] KALKULUS II 2

Kekonvergenan Barisan 0 Definisi: Barisan {an} dikatakan konvergen menuju L atau berlimit L dan ditulis sebagai Jika untuk tiap bilangan positif , ada bilangan positif N sehingga untuk Sebaliknya, barisan yang tidak konvergen ke suatu bilangan L yang terhingga dinamakan divergen. 12/5/2020 [MA 1124] KALKULUS II 3

Catatan 0 Akan kita jumpai banyak persoalan konvergensi barisan. Kita akan menggunakan fakta berikut. Jika , maka Fakta ini memudahkan karena kita dapat memakai kaidah I’ Hospital untuk soal peubah kontinu. 12/5/2020 [MA 1124] KALKULUS II 4

Sifat Limit Barisan 0 Sifat dari limit barisan, jika barisan {an} konvergen ke L dan barisan {bn} konvergen ke M, maka 0 Barisan {an} dikatakan 12/5/2020 [MA 1124] KALKULUS II 5

Contoh Tentukan konvergensi dari barisan di bawah ini: 1. Jawab: Ambil , Dalam hal ini menurut kaidah I’Hospital, Jadi, artinya barisan an konvergen menuju ½. 12/5/2020 [MA 1124] KALKULUS II 6

Contoh 2. Jawab: Ambil I’Hospital, , Dalam hal ini menurut kaidah Jadi, artinya barisan an konvergen menuju e. 12/5/2020 [MA 1124] KALKULUS II 7

Latihan Tentukan konvergensi dari barisan di bawah ini: 1. 7. 2. 8. 3. 4. 9. 10. 5. 6. 12/5/2020 11. [MA 1124] KALKULUS II 8

Deret Tak Hingga 0 Bentuk deret tak hingga dinotasikan dengan notasi sigma, sebagai berikut: dengan an adalah suku ke-n. 12/5/2020 [MA 1124] KALKULUS II 9

Barisan Jumlah Parsial Misalkan Sn menyatakan jumlah parsial ke-n suku deret , maka S 1 = a 1 S 2 = a 1 + a 2. . . Sn = a 1 + a 2 + a 3 + a 4 + …+ an = Barisan {Sn}, dinamakan barisan jumlah parsial deret Dari jumlah parsial ini di dapat bahwa Sn – Sn-1 = an. 12/5/2020 [MA 1124] KALKULUS II 10

Kekonvergenan Deret Tak Hingga Deret tak hingga konvergen dan mempunyai jumlah S jika barisan jumlah-jumlah parsialnya {Sn} konvergen ke S. Sebaliknya apabila {Sn} divergen maka deret divergen. 12/5/2020 [MA 1124] KALKULUS II 11

Deret Geometri 0 Bentuk umum deret geometri adalah 0 dengan a 0. Jumlah parsial deret ini adalah dan dapat ditulis sebagai 12/5/2020 [MA 1124] KALKULUS II 12

Sifat Deret Geometri 1. Jika maka barisan {rn} konvergen ke 0 karena maka deretnya konvergen ke 2. Jika maka barisan {rn} divergen karena maka deretnya juga divergen 12/5/2020 [MA 1124] KALKULUS II 13

Contoh (Selidiki kekonvergenannya) 1. Jawab: Kalau kita perhatikan Sehingga kita peroleh jumlah parsial ke-n-nya Dan Jadi karena barisan jumlah-jumlah parsialnya konvergen ke 1, maka deret di atas juga konvergen. 12/5/2020 [MA 1124] KALKULUS II 14

Contoh (2) 2. (Deret Kolaps) Jawab: Kalau kita perhatikan Dari sini kita peroleh bahwa jumlah parsial ke-n-nya Dan Jadi karena barisan jumlah parsialnya konvergen ke 1, maka deret di atas juga konvergen. 12/5/2020 [MA 1124] KALKULUS II 15

Contoh (3) 3. (Deret Harmonik) Jawab: Dari sini kita dapatkan Sehingga akan kita dapatkan limit untuk Sn untuk n menuju tak hingga harganya adalah tak hingga juga. Jadi deret harmonik di atas adalah deret divergen. 12/5/2020 [MA 1124] KALKULUS II 16

Uji kedivergenan dengan suku ke-n. Apabila konvergen maka = 0, ekivalen 0 maka deret divergen. Contoh: Buktikan bahwa divergen. Bukti = = Jadi terbukti bahwa 12/5/2020 (Tidak Nol) divergen. [MA 1124] KALKULUS II 17

Masalah Baru = 0, tetapi dari sini Dalam banyak kasus bahwa kita sangat sulit menentukan apakah deret tersebut konvergen atau divergen. Sebagai contoh deret harmonik, =1 + Jelas bahwa +. . . = 0, tetapi deret harmonik adalah deret yang divergen. Oleh karena itu perlu dilakukan uji-uji untuk deret positif. 12/5/2020 [MA 1124] KALKULUS II 18

Uji Deret Positif 1. Tes Integral Misalkan fungsi f kontinu monoton turun dan f(x) > 0 pada selang [1, ) konvergen, maka deret a. Jika integral tak wajar konvergen. b. Jika integral tak wajar divergen. 12/5/2020 [MA 1124] KALKULUS II divergen, maka deret 19

Contoh 1. Selidiki kekonvergenan dari Jawab. Kita ambil , sehingga = = Jadi karena = konvergen, maka juga konvergen. 12/5/2020 [MA 1124] KALKULUS II 20

Contoh 2. Selidiki kekonvergenan dari Jawab. Kita ambil Jadi karena , sehingga divergen, maka juga divergen. 12/5/2020 [MA 1124] KALKULUS II 21

Latihan Selidiki kekonvergenan deret berikut: 1. 4. 2. 5. 3. 12/5/2020 [MA 1124] KALKULUS II 22

Uji Deret Positif 2. Uji Deret -p Deret-p atau deret hiperharmonik mempunyai bentuk umum Dengan menggunakan tes integral, kita dapatkan = = Kalau kita perhatikan, untuk 1. p = 1 diperoleh deret harmonik, sehingga untuk p = 1 2. deret divergen. = 0, sehingga diperoleh deret 2. p > 1 maka yang konvergen. 12/5/2020 [MA 1124] KALKULUS II 23

Uji Deret Positif 3. p < 1 maka divergen. =∞, sehingga diperoleh deret yang 4. p < 0, suku ke-n deret , yaitu, tidak menuju 0. Jadi deret divergen menurut Uji Suku ke-n Sehingga dapat kita simpulkan untuk uji deret-p, yaitu: 1. Deret-p konvergen apabila p > 1 2. Deret-p divergen apabila 0 p 1 12/5/2020 [MA 1124] KALKULUS II 24

Contoh Apakah deret berikut konvergen atau divergen? 1. Berdasarkan uji deret-p, deret konvergen karena p=1, 001 > 1 2. Berdasarkan uji deret-p, deret divergen karena p= ½ < 1 12/5/2020 [MA 1124] KALKULUS II 25

Uji Deret Positif 3. Tes Perbandingan deret lain Andaikan deret positif, jika an bn maka 1. Jika konvergen, maka 2. Jika divergen, maka 12/5/2020 [MA 1124] KALKULUS II konvergen divergen 26

Contoh Selidiki Kekonvergenan deret berikut: 1. Jawab: Akan kita bandingkan deret ini dengan kita tahu bahwa , dan bn= adalah deret harmonik dan , Sehingga karena deret divergen, maka deret yang divergen. 12/5/2020 [MA 1124] KALKULUS II 27

Contoh 2. Jawab: Akan kita bandingkan deret ini dengan bn= kita tahu bahwa p = 2 >1 dan konvergen, maka 12/5/2020 dan an= adalah deret hiperharmonik dengan , Sehingga karena deret yang konvergen. [MA 1124] KALKULUS II 28

Latihan Selidiki kekonvergenan deret berikut 1. 4. 2. 5. 3. 12/5/2020 [MA 1124] KALKULUS II 29

Uji Deret Positif 4. Tes Banding limit Andaikan an dan bn deret positif dan 1. Jika 0 < L < maka dan =L sama-sama konvergen atau divergen 2. Jika L = 0 dan 12/5/2020 konvergen maka [MA 1124] KALKULUS II konvergen. 30

Contoh Selidiki kekonvergenan dari deret berikut : 1. Jawab: Kita gunakan Uji Banding Limit. Kalau kita perhatikan deret tersebut, suku umumnya mirip dengan bn= sehingga =2 Jadi karena L=2 dan konvergen, maka deret konvergen. 12/5/2020 [MA 1124] KALKULUS II 31

Contoh Selidiki kekonvergenan dari deret berikut : 2. Jawab: Kita gunakan Uji Banding Limit. Kalau kita perhatikan deret tersebut, suku umumnya mirip dengan bn= sehingga =1 = = Jadi karena L=1 dan divergen, maka deret divergen. 12/5/2020 [MA 1124] KALKULUS II 32

Latihan Selidiki kekonvergenan dari deret berikut: 1. 4. 2. 5. 3. 12/5/2020 [MA 1124] KALKULUS II 33

Uji Deret Positif 5. Tes Hasil Bagi Diketahui merupakan suatu deret dengan suku-suku yang positif, misalkan 1. Jika < 1 maka deret konvergen 2. Jika > 1 maka deret divergen 3. Jika = 1 maka uji deret ini tidak dapat dilakukan. 12/5/2020 [MA 1124] KALKULUS II 34

Contoh Selidiki kekonvergenan deret berikut: 1. Jawab: Misalkan suku ke-n adalah an = adalah an+1= sehingga , maka suku ke-n+1 Karena nilai limit r=0 (< 1), maka deret 12/5/2020 [MA 1124] KALKULUS II konvergen 35

Contoh 2. Jawab: Misalkan suku ke-n adalah an = adalah an+1= sehingga , maka suku ke-n+1 Karena nilai limit r=3 (> 1), maka deret 12/5/2020 [MA 1124] KALKULUS II divergen 36

Latihan Selidiki kekonvergenan dari deret berikut: 1. 4. 2. 5. 3. 12/5/2020 [MA 1124] KALKULUS II 37

Uji Deret Positif 6. Tes Akar Diketahui merupakan suatu deret dengan suku-suku yang positif, misalkan 1. Jika a < 1 maka deret konvergen 2. Jika a > 1 maka deret divergen 3. Jika a = 1 maka uji deret ini tidak dapat dilakukan. 12/5/2020 [MA 1124] KALKULUS II 38

Contoh Selidiki kekonvergenan deret 1. Jawab: Misalkan suku ke-n adalah an = , maka nilai limitnya adalah Karena nilai limit r = 2 (> 1), maka deret divergen 12/5/2020 [MA 1124] KALKULUS II 39

Contoh 2. Jawab: Misalkan suku ke-n adalah an = , maka nilai limitnya adalah Karena nilai limit r = ½ (< 1), maka deret konvergen 12/5/2020 [MA 1124] KALKULUS II 40

Latihan Selidiki kekonvergenan dari deret berikut: 1. 3. 2. 4. 12/5/2020 [MA 1124] KALKULUS II 41

Deret Ganti Tanda dan Kekonvergenan Mutlak 0 Deret Ganti Tanda Deret ini mempunyai bentuk sebagai berikut dengan an > 0, untuk semua n. Contoh penting adalah deret harmonik berganti tanda, yaitu 12/5/2020 [MA 1124] KALKULUS II 42

Uji Deret Ganti Tanda Andaikan deret ganti tanda, deret tersebut dikatakan konvergen jika 1. an+1< an 2. Contoh Tentukan kekonvergenan deret ganti tanda berikut 1. 2. 12/5/2020 [MA 1124] KALKULUS II 43

Contoh 1. Jawab (uji ganti tanda) Dari soal diatas kita punya an= , dan an+1 = , deret tersebut konvergen jika a. an >an+1 b. Karena a dan b terpenuhi maka deret di atas konvergen. 12/5/2020 [MA 1124] KALKULUS II 44

Contoh 2. Jawab (uji ganti tanda) Dari soal diatas kita punya an= , dan an+1 = , deret tersebut konvergen jika a. an >an+1 b. Karena a dan b terpenuhi maka deret di atas konvergen. 12/5/2020 [MA 1124] KALKULUS II 45

Latihan Selidiki kekonvergenan dari deret ganti tanda berikut: 1. 4. 2. 5. 3. 12/5/2020 [MA 1124] KALKULUS II 46

Konvergen Mutlak dan Konvergen Bersyarat Suatu deret dikatakan konvergen mutlak bila harga mutlak deret tersebut konvergen. Atau dengan kata lain dikatakan konvergen mutlak jika Dan dikatakan konvergen bersyarat jika tetapi 12/5/2020 konvergen. divergen, konvergen. [MA 1124] KALKULUS II 47

Pengujian Kekonvergenan Mutlak Misalkan dengan an 0 dan = r. Maka 1. bila r < 1 maka deret konvergen mutlak 2. bila r > 1 maka deret divergen 3. bila r = 1 maka tes gagal. ` 12/5/2020 [MA 1124] KALKULUS II 48

Contoh Selidiki deret berikut konvergen bersyarat, konvergen mutlak atau divergen 1. Jawab: Dari soal diatas kita punya an= , dan an+1 = sehingga Menurut uji hasilbagi mutlak, deret ini konvergen mutlak 12/5/2020 [MA 1124] KALKULUS II 49

Contoh 2. Jawab: Dengan uji deret ganti tanda deret konvergen adalah deret divergen (buktikan!!), sedangkan (karena merupakan deret-p dengan p= ½ < 1) Jadi deret 12/5/2020 adalah konvergen bersyarat. [MA 1124] KALKULUS II 50

Latihan Selidiki apakah deret tersebut konvergen mutlak, konvergen bersyarat atau divergen: 1. 4. 2. 5. 3. 6. 12/5/2020 [MA 1124] KALKULUS II 51

Deret Pangkat Deret pangkat secara umum ada dua bentuk 1. Deret pangkat dalam x didefinisikan = a 0 + a 1 x + a 2 x 2 +. . . 2. Deret pangkat dalam (x – b) didefinisikan = a 0 + a 1 (x-b) + a 2 (x-b)2 +. . . Untuk kali ini kita bicara selang kekonvergenan / untuk harga x berapa saja deret pangkat tersebut konvergen. 12/5/2020 [MA 1124] KALKULUS II 52

Selang Kekonvergenan Selang kekonvergenan ditentukan dengan uji hasilbagi mutlak sebagai berikut: Misalkan dan 1. Jika L < 1, maka deret konvergen. 2. Jika L = 1, tidak dapat diambil kesimpulan gunakan uji deret sebelumnya. 12/5/2020 [MA 1124] KALKULUS II 53

Soal Tentukan selang kekonvergenan deret 1. 2. 3. 12/5/2020 [MA 1124] KALKULUS II 54

Jawab 1. Kita akan gunakan Uji Hasilbagi Mutlak, untuk menyelidiki kekonvergenan mutlak. Jadi deret tersebut konvergen mutlak apabila L< 1, yaitu – 2 < x < 2 Kemudian akan kita cek untuk titik ujung intervalnya yaitu x = 2 atau x = -2. q Pada x = 2 deret ini adalah deret harmonik yang divergen. 12/5/2020 [MA 1124] KALKULUS II 55

Jawab q Pada x = – 2 deret ini adalah deret harmonik berganti tanda yang konvergen. Sehingga selang kekonvergenannya adalah – 2 x < 2 12/5/2020 [MA 1124] KALKULUS II 56

Jawab(2) 2. Kita akan gunakan Uji Hasilbagi Mutlak, untuk menyelidiki kekonvergenan mutlak. Karena L = 0 < 1, maka deret selalu konvergen untuk semua nilai x. Jadi selang kekonvergenannya adalah (- , ) 12/5/2020 [MA 1124] KALKULUS II 57

Jawab(3) 3. Kita akan gunakan Uji Hasilbagi Mutlak, untuk menyelidiki kekonvergenan mutlak. Jadi deret tersebut konvergen hanya untuk x = 0. 12/5/2020 [MA 1124] KALKULUS II 58

Teorema 1 Himpunan kekonvergenan deret pangkat berbentuk selang yang berupa salah satu dari ketiga jenis berikut: 1. satu titik x = 0 2. selang (-c, c), mungkin ditambah salah satu atau keduanya titik ujungnya. 3. seluruh himpunan bilangan riil 12/5/2020 [MA 1124] KALKULUS II 59

Teorema 2 Himpunan kekonvergenan deret pangkat berbentuk selang yang berupa salah satu dari ketiga jenis berikut : 1. satu titik x = b 2. selang (b-c, c+b), mungkin ditambah salah satu atau keduanya titik ujungnya. 3. seluruh himpunan bilangan riil 12/5/2020 [MA 1124] KALKULUS II 60

Latihan Tentukan selang kekonvergenan deret pangkat berikut: 1. 2. 3. 12/5/2020 [MA 1124] KALKULUS II 61

Operasi deret pangkat Dalam pasal sebelumnya untuk deret Pertanyaan yang muncul mengenai sifat-sifat deret kuasa di atas (misal S(x)= ) misalkan bagaimana jika S(x) didiferensialkan dan jika S(x) diintegralkan. 12/5/2020 [MA 1124] KALKULUS II 62

Teorema 0 Andaikan S(x) adalah jumlah sebuah deret pangkat pada sebuah selang I; jadi S(x)= = a 0 + a 1 x + a 2 x 2 + a 3 x 3+. . . Maka 1. S’(x) = = D[a 0 + a 1 x + a 2 x 2 + a 3 x 3+. . . ] = a 1 + 2 a 2 x + 3 a 3 x 2+. . . = 2. = = a 0 x + a 1 x 2 + a 2 x 3 + a 3 x 4+. . . = 12/5/2020 [MA 1124] KALKULUS II 63

Contoh Sesuai teorema di atas = 1 + x 2 + x 3 +. . . untuk -1< x <1, tentukan a. b. ln(1 – x) Jawab: a. Dengan menurunkan suku demi suku, kita peroleh = 1 + 2 x + 3 x 2 + 4 x 3 +. . . , 12/5/2020 -1< x <1 [MA 1124] KALKULUS II 64

Contoh a. ln (1 – x) Sedangkan dengan mengintegralkan suku demi suku, kita peroleh juga , 12/5/2020 -1< x <1 [MA 1124] KALKULUS II 65

Latihan Tentukan (Petunjuk : Lihat contoh a dan b di atas) 1. 5. f(x)=tan-1(x) 2. 6. 3. 7. 4. 12/5/2020 [MA 1124] KALKULUS II 66

Deret Taylor dan Deret Maclurin Deret Taylor 0 Definisi: Misalkan f(x) dapat diturunkan sampai n kali pada x=b. Maka f(x) dapat diperderetkan menjadi deret kuasa dalam bentuk f(x) = = f(b) + f ’(b)(x-b)+ +. . . deret di atas disebut Deret Taylor dengan pusat x = b. Bila b = 0, kita peroleh Deret Mac Laurin, yaitu f(x) = 12/5/2020 = f(0) + f ’(0)(x)+ [MA 1124] KALKULUS II +. . . 67

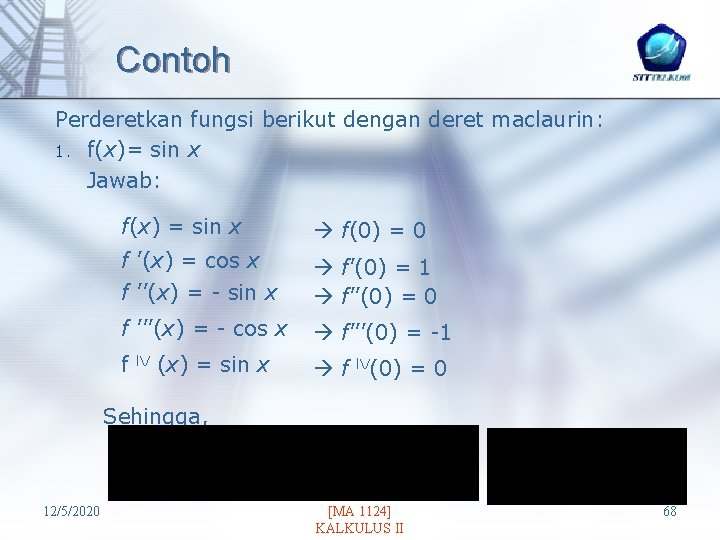
Contoh Perderetkan fungsi berikut dengan deret maclaurin: 1. f(x)= sin x Jawab: f(x) = sin x f(0) = 0 f ’(x) = cos x f ’’(x) = - sin x f’(0) = 1 f’’(0) = 0 f ’’’(x) = - cos x f’’’(0) = -1 f f l. V(0) = 0 l. V (x) = sin x Sehingga, 12/5/2020 [MA 1124] KALKULUS II 68

Contoh 2. f(x)= ex Jawab: f(x) = ex f(0) = 1 f ’(x) = ex f ’’(x) = ex f’(0) = 1 f’’(0) = 1 f ’’’(x) = ex f’’’(0) = 1 f f l. V(0) = 1 l. V (x) = ex Sehingga, 12/5/2020 [MA 1124] KALKULUS II 69

Contoh 3. Perderetkan f(x)= ex dengan deret taylor dengan pusat di x=1 Jawab: f(x) = ex f(1) = e f ’(x) = ex f ’’(x) = ex f’(1) = e f’’(1) = e f ’’’(x) = ex f’’’(1) = e f f l. V(1) = e l. V (x) = ex Sehingga, 12/5/2020 [MA 1124] KALKULUS II 70

Latihan 1. Perderetkan dengan f(x) berikut deret maclaurin a. f(x) = cos x e. f(x) = sin 2 x b. f(x) = cos x 2 f. f(x) = sec x c. f(x) = cos 2 x g. f(x) = tan x d. f(x) = ex + sin x h. f(x) = sec x 2. Perderetkan dengan f(x) berikut deret taylor dengan pusat x = a a. f(x) = cos x, a = /3 c. f(x) = ex, a = 2 b. f(x) = sin x, a = /3 12/5/2020 [MA 1124] KALKULUS II 71