Program Analysis via Graph Reachability Thomas Reps University

Program Analysis via Graph Reachability Thomas Reps University of Wisconsin http: //www. cs. wisc. edu/~reps/ PLDI 00 Tutorial, Vancouver, B. C. , June 18, 2000

PLDI 00 Registration Form • PLDI 00: …………. . $ ____ • Tutorial (morning): …………… $ ____ • Tutorial (afternoon): …………. . $ ____ • Tutorial (evening): ……………. $ – 0 –

Applications • Program optimization • Program-understanding and software -reengineering • Security – information flow • Verification – model checking – security of crypto-based protocols for distributed systems

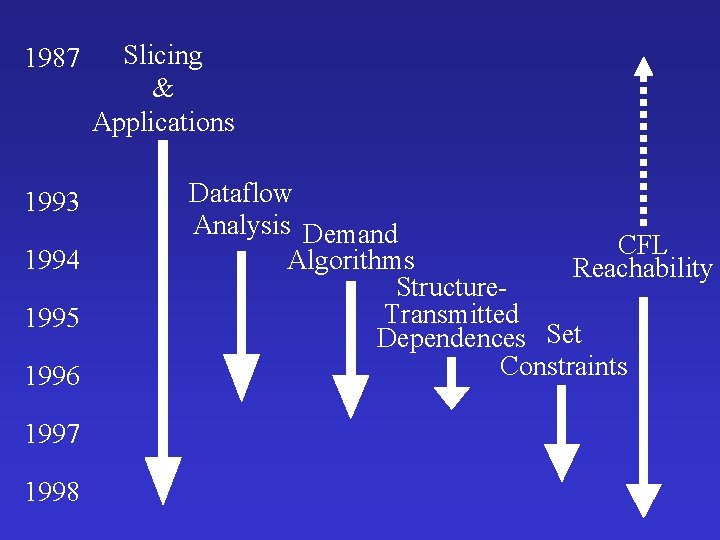
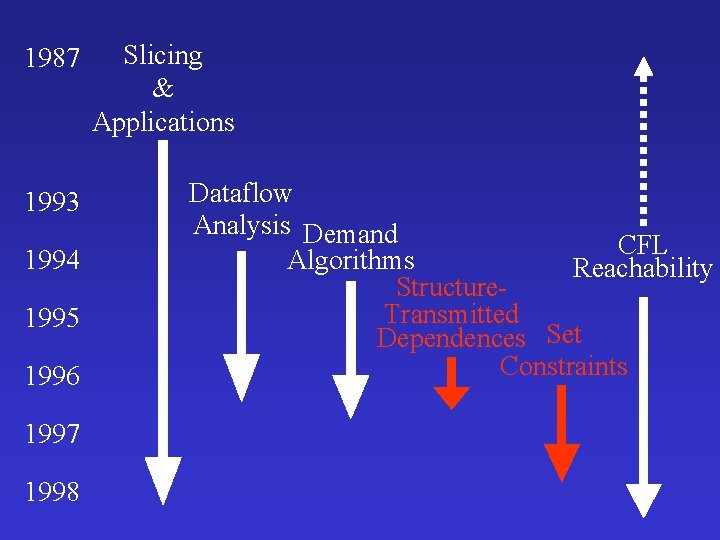
1987 1993 1994 1995 1996 1997 1998 Slicing & Applications Dataflow Analysis Demand CFL Algorithms Reachability Structure. Transmitted Dependences Set Constraints

. . . As Well As. . . • Flow-insensitive points-to analysis • Complexity results – Linear. . . cubic. . . undecidable variants – PTIME-completeness • Model checking of recursive hierarchical finite-state machines – “infinite”-state systems – linear-time and cubic-time algorithms

. . . And Also • Analysis of attribute grammars • Security of crypto-based protocols for distributed systems [Dolev, Even, & Karp 83] • Formal-language problems – CFL-recognition (given G and , is L(G)? ) – 2 DPDA- and 2 NPDA-simulation • Given M and , is L(M)? • String-matching problems

Unifying Conceptual Model for Dataflow-Analysis Literature • • • Linear-time gen-kill [Hecht 76], [Kou 77] Path-constrained DFA [Holley & Rosen 81] Linear-time GMOD [Cooper & Kennedy 88] Flow-sensitive MOD [Callahan 88] Linear-time interprocedural gen-kill [Knoop & Steffen 93] • Linear-time bidirectional gen-kill [Dhamdhere 94] • Relationship to interprocedural DFA [Sharir & Pneuli 81], [Knoop & Steffen 92]

Collaborators • • Susan Horwitz Mooly Sagiv Genevieve Rosay David Melski • David Binkley • Michael Benedikt • Patrice Godefroid

Themes • Harnessing CFL-reachability • Relationship to other analysis paradigms • Exhaustive alg. Demand alg. • Understanding complexity – Linear. . . cubic. . . undecidable • Beyond CFL-reachability

Backward Slice int main() { int sum = 0; int i = 1; while (i < 11) { sum = sum + i; i = i + 1; } printf(“%dn”, sum); printf(“%dn”, i); } Backward slice with respect to “printf(“%dn”, i)”

Backward Slice int main() { int sum = 0; int i = 1; while (i < 11) { sum = sum + i; i = i + 1; } printf(“%dn”, sum); printf(“%dn”, i); } Backward slice with respect to “printf(“%dn”, i)”

Slice Extraction int main() { int i = 1; while (i < 11) { i = i + 1; } printf(“%dn”, i); } Backward slice with respect to “printf(“%dn”, i)”

Forward Slice int main() { int sum = 0; int i = 1; while (i < 11) { sum = sum + i; i = i + 1; } printf(“%dn”, sum); printf(“%dn”, i); } Forward slice with respect to “sum = 0”

Forward Slice int main() { int sum = 0; int i = 1; while (i < 11) { sum = sum + i; i = i + 1; } printf(“%dn”, sum); printf(“%dn”, i); } Forward slice with respect to “sum = 0”

What Are Slices Useful For? • Understanding Programs – What is affected by what? • Restructuring Programs – Isolation of separate “computational threads” • Program Specialization and Reuse – Slices = specialized programs – Only reuse needed slices • Program Differencing – Compare slices to identify changes • Testing – What new test cases would improve coverage? – What regression tests must be rerun after a change?

Line-Character-Count Program void line_char_count(FILE *f) { int lines = 0; int chars; BOOL eof_flag = FALSE; int n; extern void scan_line(FILE *f, BOOL *bptr, scan_line(f, &eof_flag, &n); chars = n; while(eof_flag == FALSE){ lines = lines + 1; scan_line(f, &eof_flag, &n); chars = chars + n; } printf(“lines = %dn”, lines); printf(“chars = %dn”, chars); } int *iptr);

Character-Count Program void char_count(FILE *f) { int lines = 0; int chars; BOOL eof_flag = FALSE; int n; extern void scan_line(FILE *f, BOOL *bptr, scan_line(f, &eof_flag, &n); chars = n; while(eof_flag == FALSE){ lines = lines + 1; scan_line(f, &eof_flag, &n); chars = chars + n; } printf(“lines = %dn”, lines); printf(“chars = %dn”, chars); } int *iptr);

Line-Character-Count Program void line_char_count(FILE *f) { int lines = 0; int chars; BOOL eof_flag = FALSE; int n; extern void scan_line(FILE *f, BOOL *bptr, scan_line(f, &eof_flag, &n); chars = n; while(eof_flag == FALSE){ lines = lines + 1; scan_line(f, &eof_flag, &n); chars = chars + n; } printf(“lines = %dn”, lines); printf(“chars = %dn”, chars); } int *iptr);

Line-Count Program void line_count(FILE *f) { int lines = 0; int chars; BOOL eof_flag = FALSE; int n; extern void scan_line 2(FILE *f, BOOL *bptr, scan_line 2(f, &eof_flag, &n); chars = n; while(eof_flag == FALSE){ lines = lines + 1; scan_line 2(f, &eof_flag, &n); chars = chars + n; } printf(“lines = %dn”, lines); printf(“chars = %dn”, chars); } int *iptr);

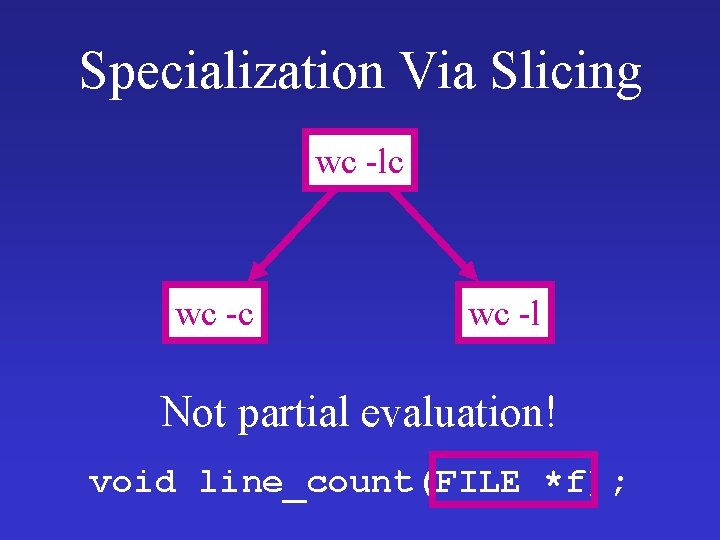
Specialization Via Slicing wc -lc wc -l Not partial evaluation! void line_count(FILE *f);

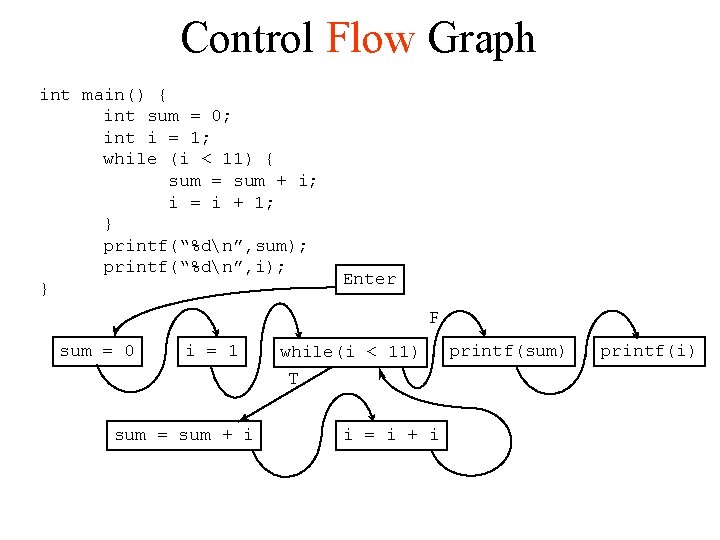
Control Flow Graph int main() { int sum = 0; int i = 1; while (i < 11) { sum = sum + i; i = i + 1; } printf(“%dn”, sum); printf(“%dn”, i); } Enter F sum = 0 i = 1 while(i < 11) T sum = sum + i i = i + i printf(sum) printf(i)

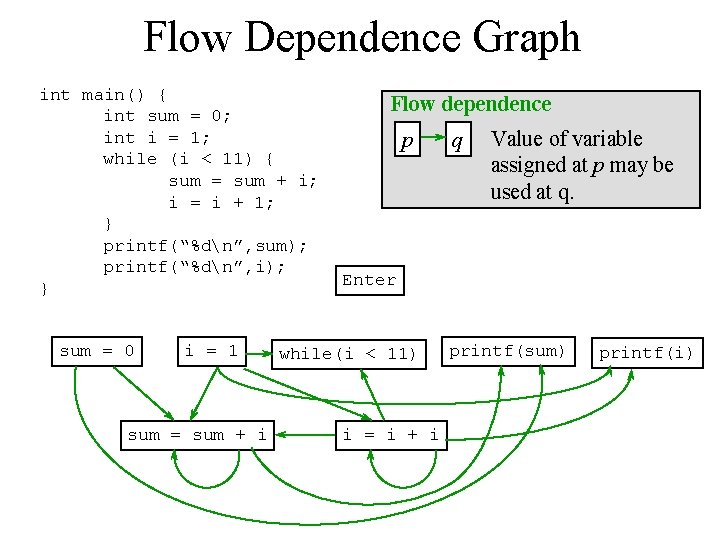
Flow Dependence Graph int main() { int sum = 0; int i = 1; while (i < 11) { sum = sum + i; i = i + 1; } printf(“%dn”, sum); printf(“%dn”, i); } sum = 0 i = 1 sum = sum + i Flow dependence p q Value of variable assigned at p may be used at q. Enter while(i < 11) i = i + i printf(sum) printf(i)

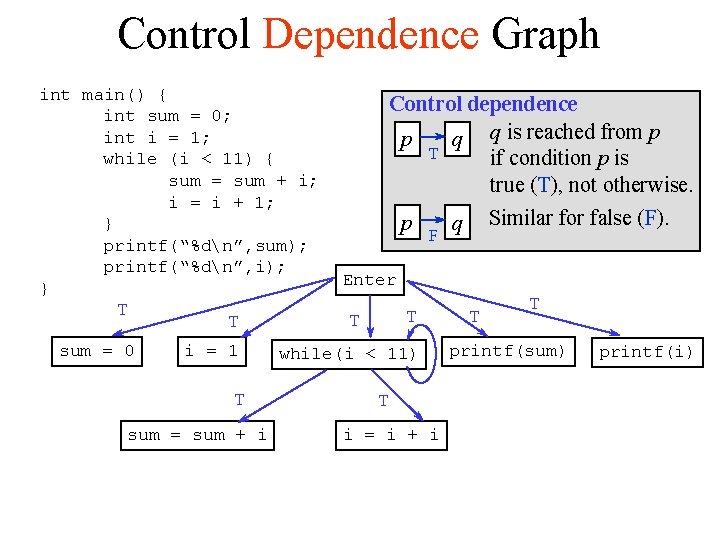
Control Dependence Graph int main() { int sum = 0; int i = 1; while (i < 11) { sum = sum + i; i = i + 1; } printf(“%dn”, sum); printf(“%dn”, i); } T sum = 0 T i = 1 T sum = sum + i Control dependence p q q is reached from p T if condition p is true (T), not otherwise. p F Similar for false (F). q Enter T T while(i < 11) T i = i + i T T printf(sum) printf(i)

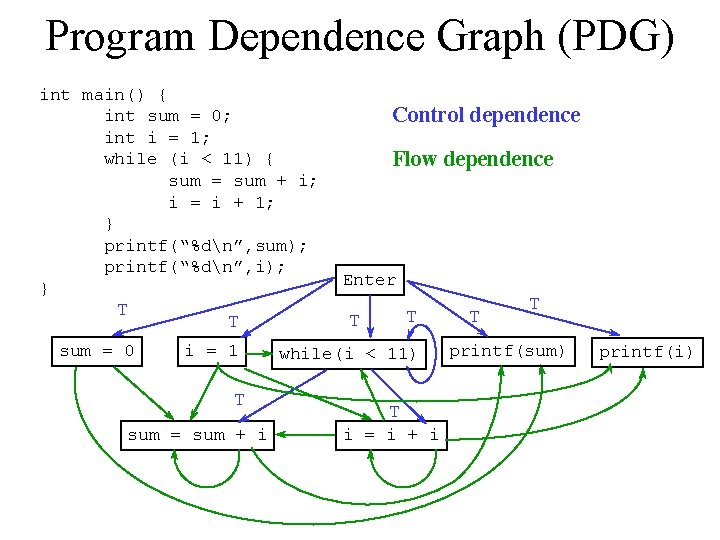
Program Dependence Graph (PDG) int main() { int sum = 0; int i = 1; while (i < 11) { sum = sum + i; i = i + 1; } printf(“%dn”, sum); printf(“%dn”, i); } T sum = 0 T i = 1 T sum = sum + i Control dependence Flow dependence Enter T T while(i < 11) T i = i + i T T printf(sum) printf(i)

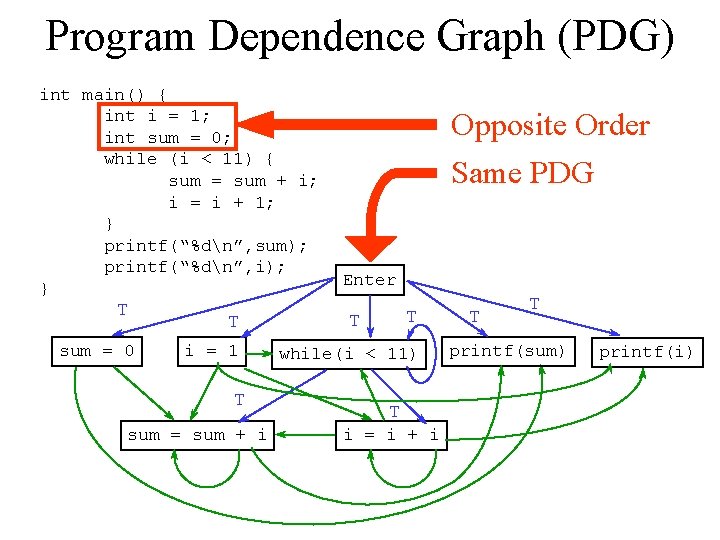
Program Dependence Graph (PDG) int main() { int i = 1; int sum = 0; while (i < 11) { sum = sum + i; i = i + 1; } printf(“%dn”, sum); printf(“%dn”, i); } T sum = 0 T i = 1 T sum = sum + i Opposite Order Same PDG Enter T T while(i < 11) T i = i + i T T printf(sum) printf(i)

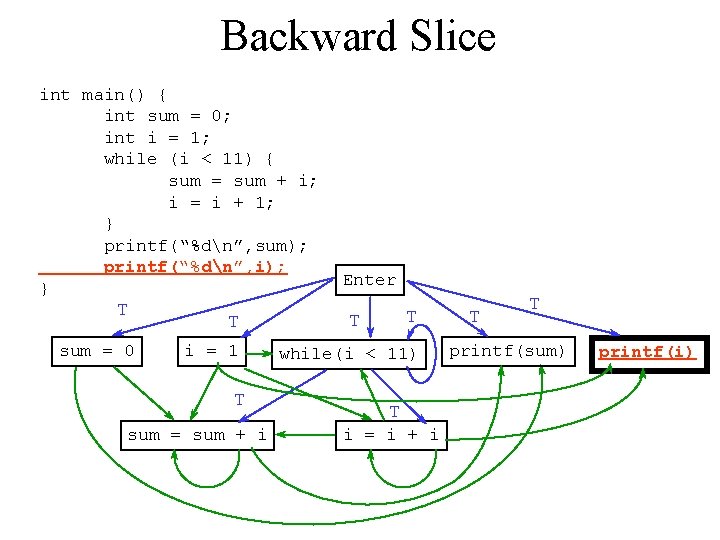
Backward Slice int main() { int sum = 0; int i = 1; while (i < 11) { sum = sum + i; i = i + 1; } printf(“%dn”, sum); printf(“%dn”, i); } T sum = 0 T i = 1 T sum = sum + i Enter T T while(i < 11) T i = i + i T T printf(sum) printf(i)

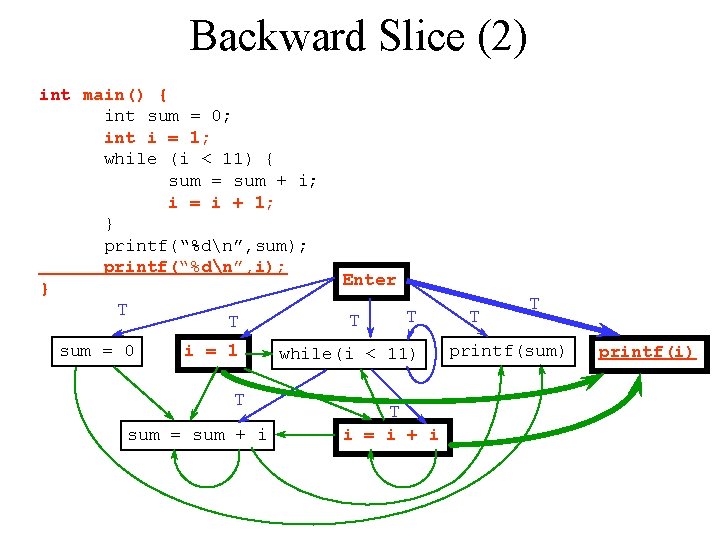
Backward Slice (2) int main() { int sum = 0; int i = 1; while (i < 11) { sum = sum + i; i = i + 1; } printf(“%dn”, sum); printf(“%dn”, i); } T sum = 0 T i = 1 T sum = sum + i Enter T T while(i < 11) T i = i + i T T printf(sum) printf(i)

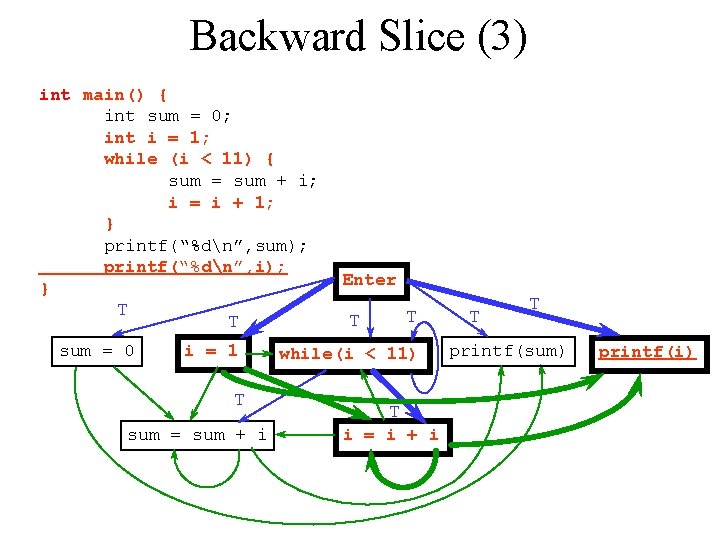
Backward Slice (3) int main() { int sum = 0; int i = 1; while (i < 11) { sum = sum + i; i = i + 1; } printf(“%dn”, sum); printf(“%dn”, i); } T sum = 0 T i = 1 T sum = sum + i Enter T T while(i < 11) T i = i + i T T printf(sum) printf(i)

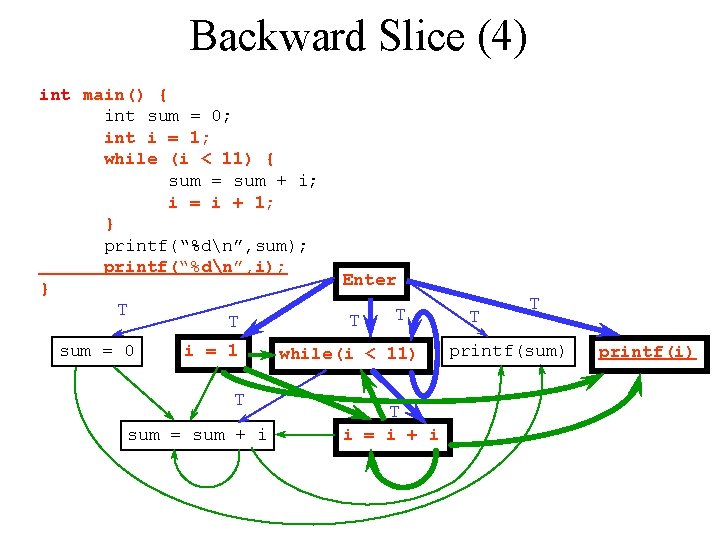
Backward Slice (4) int main() { int sum = 0; int i = 1; while (i < 11) { sum = sum + i; i = i + 1; } printf(“%dn”, sum); printf(“%dn”, i); } T sum = 0 T i = 1 T sum = sum + i Enter T T while(i < 11) T i = i + i T T printf(sum) printf(i)

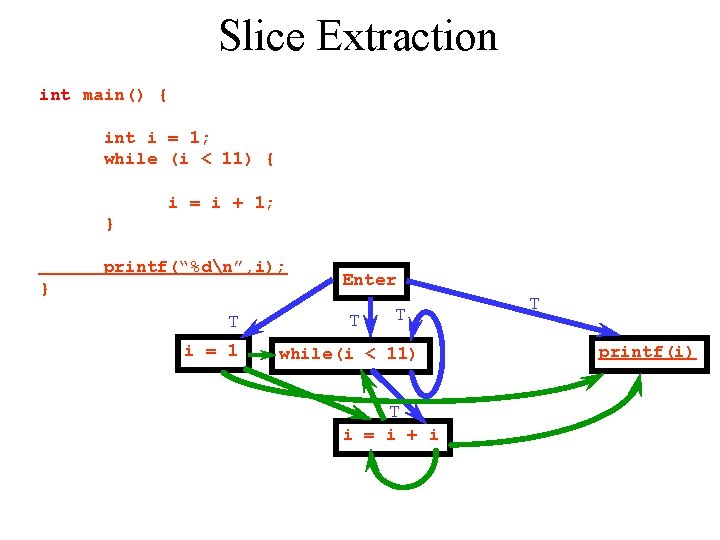
Slice Extraction int main() { int i = 1; while (i < 11) { i = i + 1; } printf(“%dn”, i); } T i = 1 Enter T T while(i < 11) T i = i + i T printf(i)

Code. Surfer

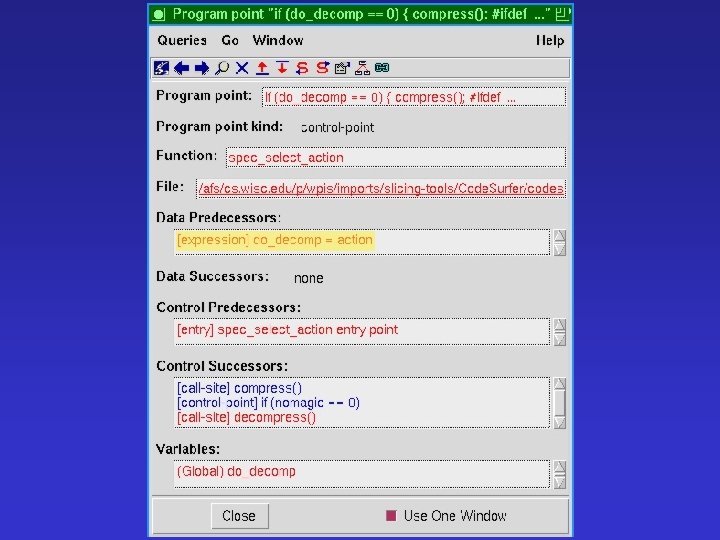
Browsing a Dependence Graph Pretend this is your favorite browser What does clicking on a link do? Or you move to an internal tag You get a new page

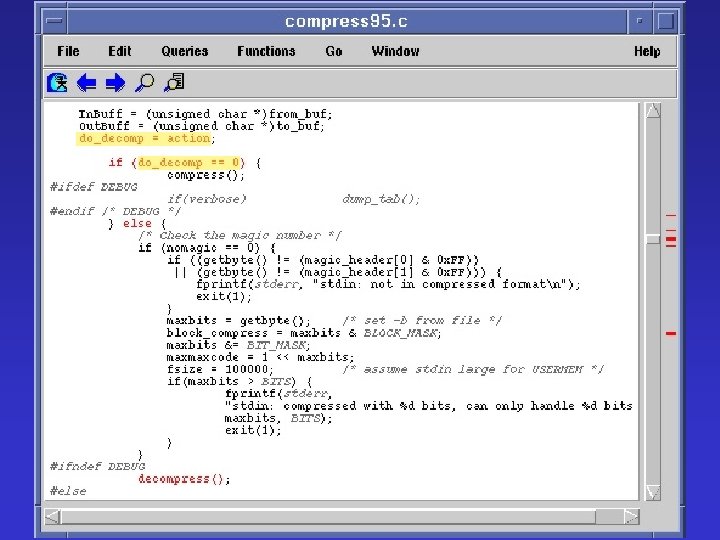
Interprocedural Slice int main() { int add(int x, int y) { int sum = 0; return x + y; int i = 1; } while (i < 11) { sum = add(sum, i); i = add(i, 1); } printf(“%dn”, sum); printf(“%dn”, i); } Backward slice with respect to “printf(“%dn”, i)”

Interprocedural Slice int main() { int add(int x, int y) { int sum = 0; return x + y; int i = 1; } while (i < 11) { sum = add(sum, i); i = add(i, 1); } printf(“%dn”, sum); printf(“%dn”, i); } Backward slice with respect to “printf(“%dn”, i)”

Interprocedural Slice int main() { int add(int x, int y) { int sum = 0; return x + y; int i = 1; } while (i < 11) { sum = add(sum, i); i = add(i, 1); } printf(“%dn”, sum); printf(“%dn”, i); } Superfluous components included by Weiser’s slicing algorithm [TSE 84] Left out by algorithm of Horwitz, Reps, & Binkley [PLDI 88; TOPLAS 90]

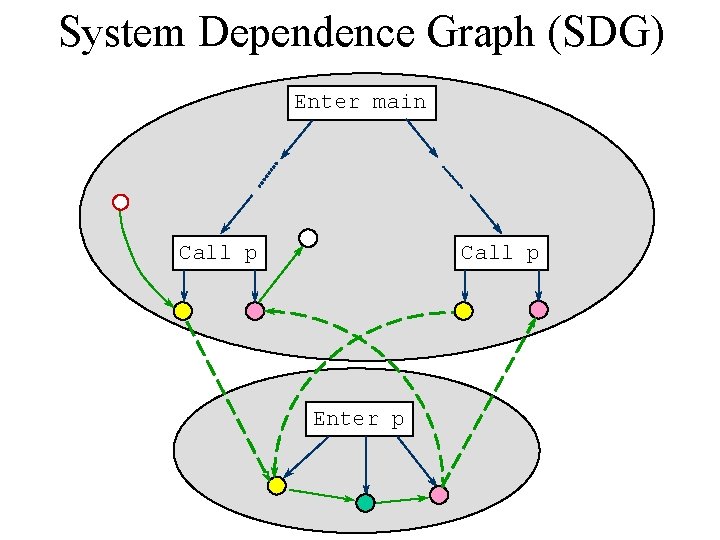
System Dependence Graph (SDG) Enter main Call p Enter p

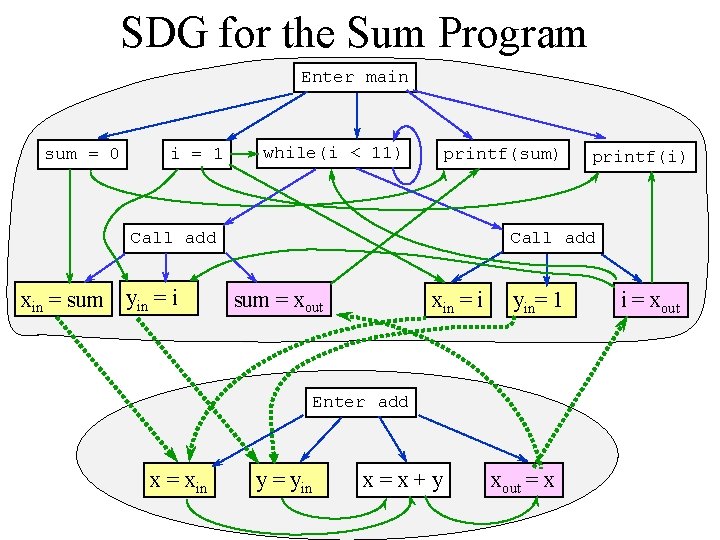
SDG for the Sum Program Enter main sum = 0 i = 1 while(i < 11) printf(sum) Call add xin = sum yin = i sum = xout xin = i yin= 1 Enter add x = xin printf(i) y = yin x=x+y xout = x i = xout

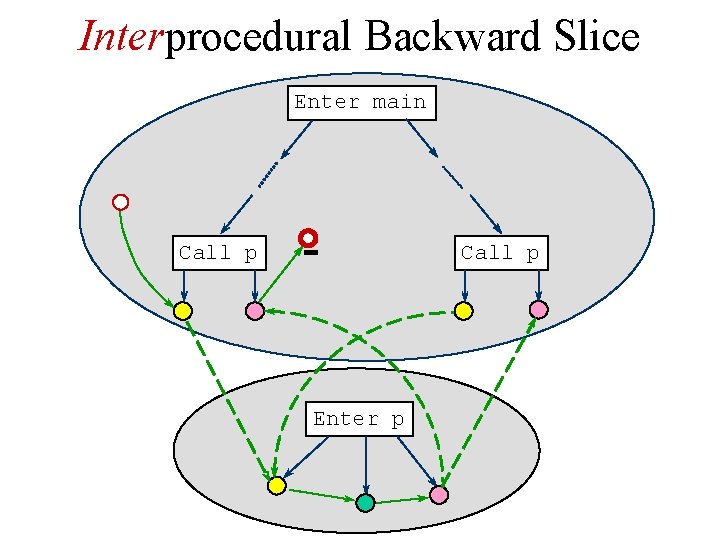
Interprocedural Backward Slice Enter main Call p Enter p

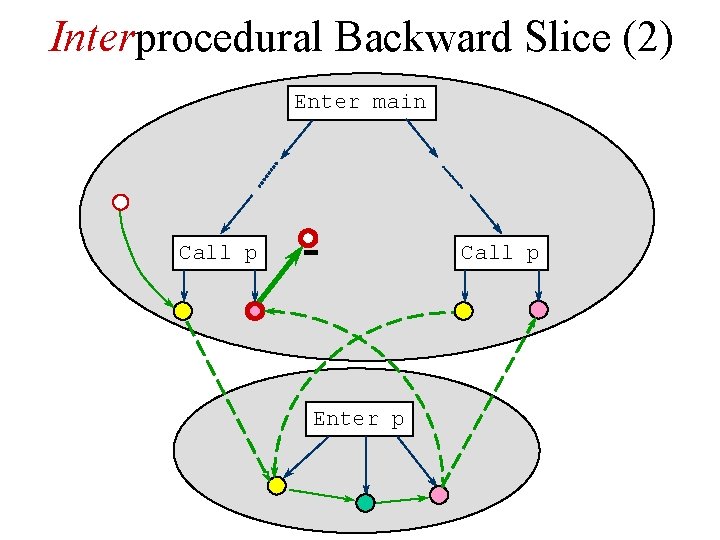
Interprocedural Backward Slice (2) Enter main Call p Enter p

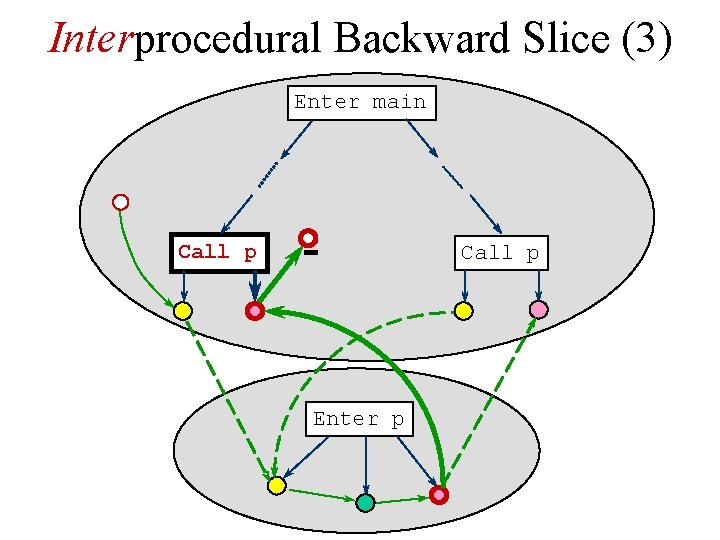
Interprocedural Backward Slice (3) Enter main Call p Enter p

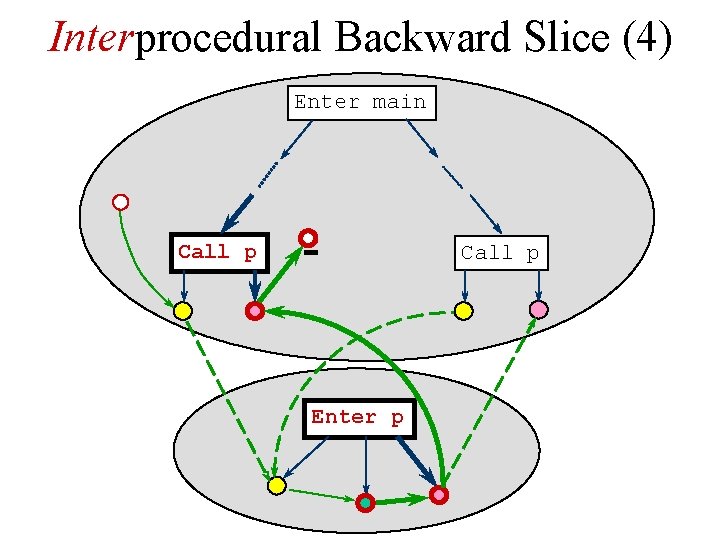
Interprocedural Backward Slice (4) Enter main Call p Enter p

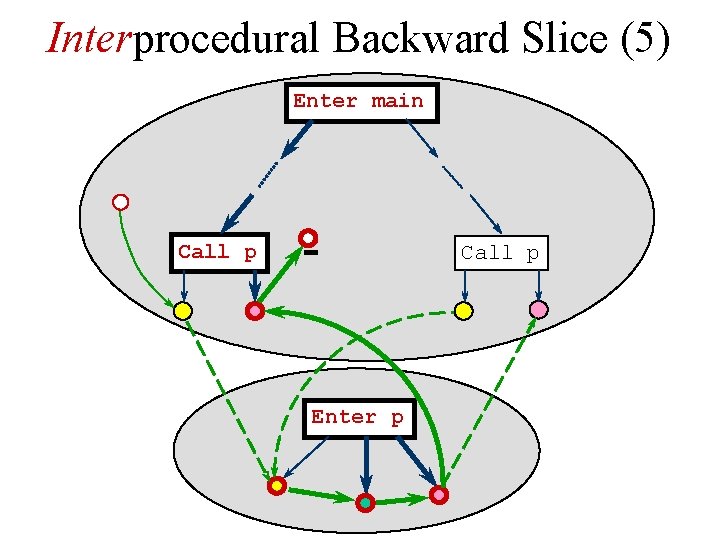
Interprocedural Backward Slice (5) Enter main Call p Enter p

Interprocedural Backward Slice (6) Enter main Call p ) ( [ ] Enter p

Matched-Parenthesis Path ( ) [ )

Interprocedural Backward Slice (6) Enter main Call p Enter p

Interprocedural Backward Slice (7) Enter main Call p Enter p

Slice Extraction Enter main Call p Enter p

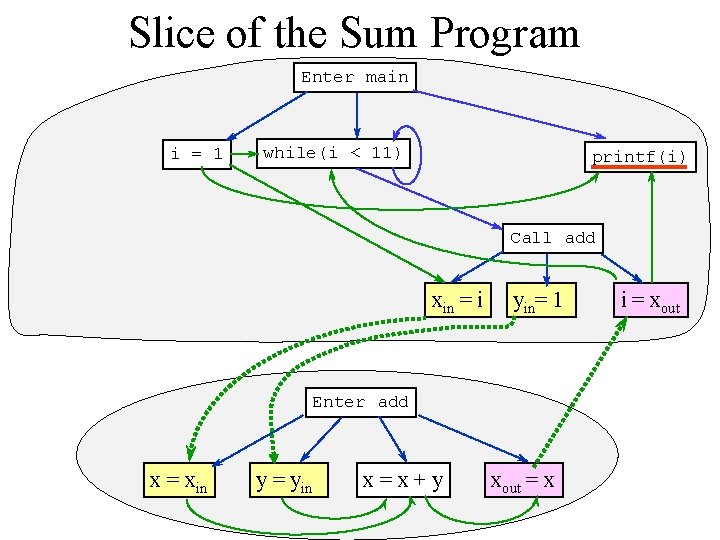
Slice of the Sum Program Enter main i = 1 while(i < 11) printf(i) Call add xin = i yin= 1 Enter add x = xin y = yin x=x+y xout = x i = xout

CFL-Reachability [Yannakakis 90] • G: Graph (N nodes, E edges) • L: A context-free language • L-path from s to t iff • Running time: O(N 3)

Interprocedural Slicing via CFL-Reachability • Graph: System dependence graph • L: L(matched) [roughly] • Node m is in the slice w. r. t. n iff there is an L(matched)-path from m to n

Asymptotic Running Time [Reps, Horwitz, Sagiv, & Rosay 94] • CFL-reachability – System dependence graph: N nodes, E edges – Running time: O(N 3) • System dependence graph Special structure Running time: O(E + Call. Sites % Max. Params 3)

matched | | ( e [ e ] ] e ) ] e [ s ( e [ matched ] ( matched ) matched e e [ e ] ] Ordinary CFL-Reachability Graph Reachability e ) t

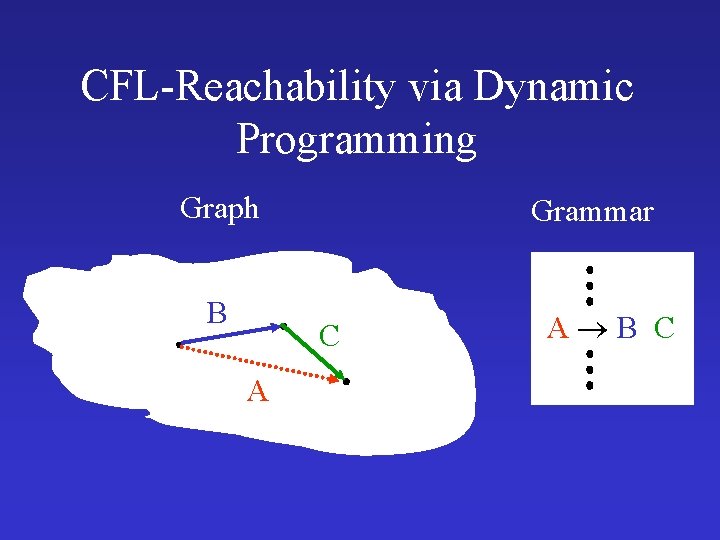
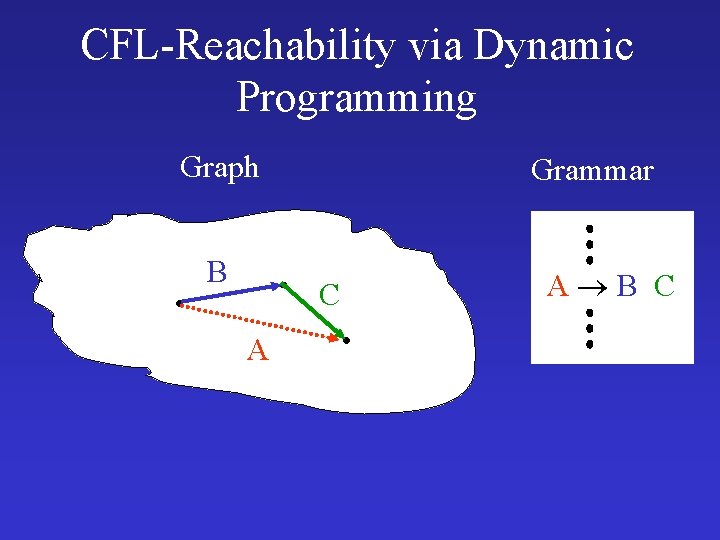
CFL-Reachability via Dynamic Programming Graph B Grammar C A A B C

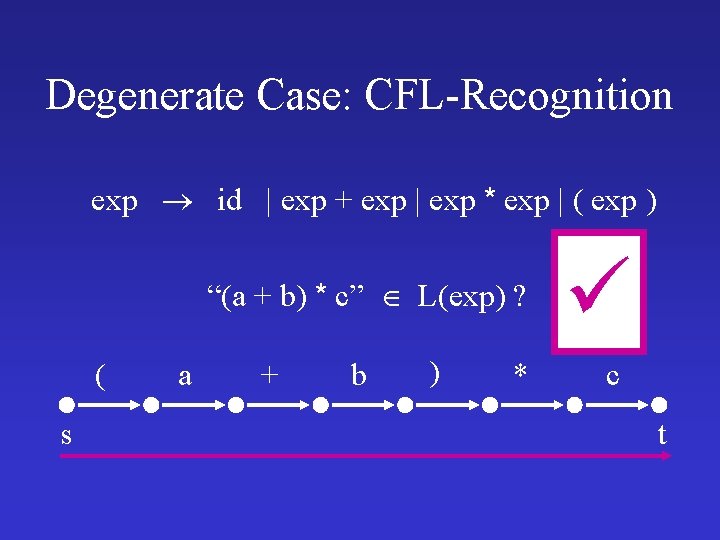
Degenerate Case: CFL-Recognition exp id | exp + exp | exp * exp | ( exp ) “(a + b) * c” L(exp) ? ( s a + b ) * c t

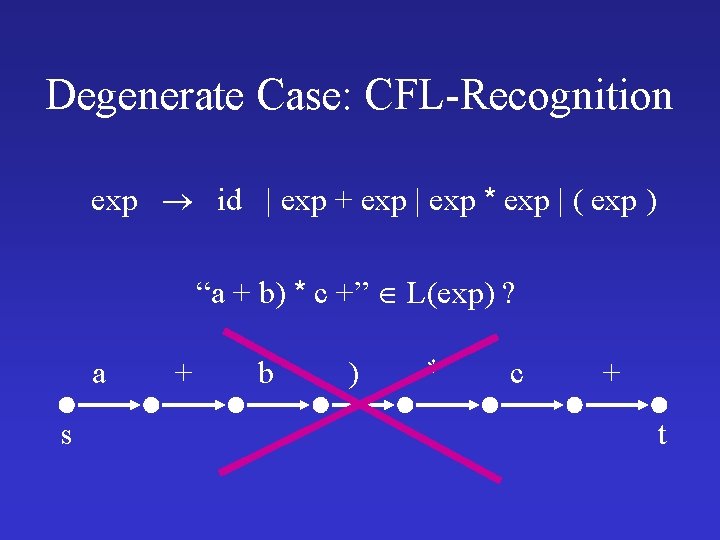
Degenerate Case: CFL-Recognition exp id | exp + exp | exp * exp | ( exp ) “a + b) * c +” L(exp) ? a s + b ) * c + t

CYK: Context-Free Recognition M M M | ( M ) | [ M ] | ( ) | [ ] = “( [ ] ) [ ]” Is L(M)?

CYK: Context-Free Recognition M M M | ( M ) | [ M ] | ( ) | [ ] M M M | LPM ) | LBM ] | ( ) | [ ] LPM ( M LBM [ M

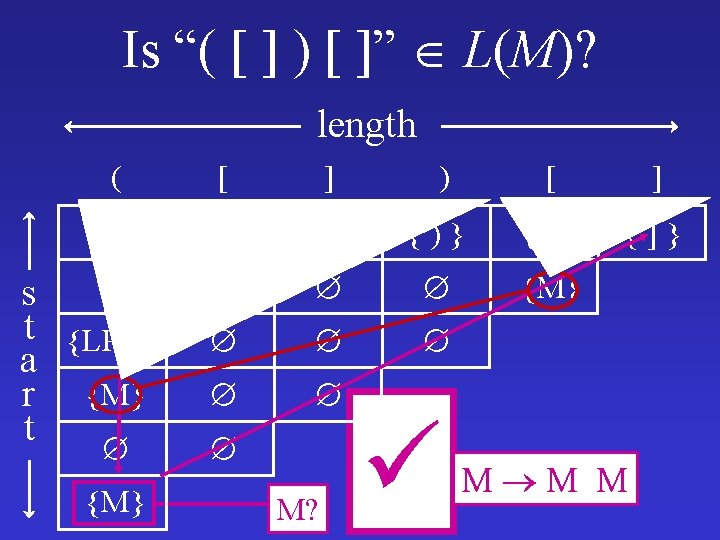
CYK: Graphs vs. Tables Is “( [ ] ) [ ]” L(M)? ( s [ ] ) [ M LPM M | LPM ) LPM ( M ] M M | M t LBM ] | ( ) | [ ] LBM [ M

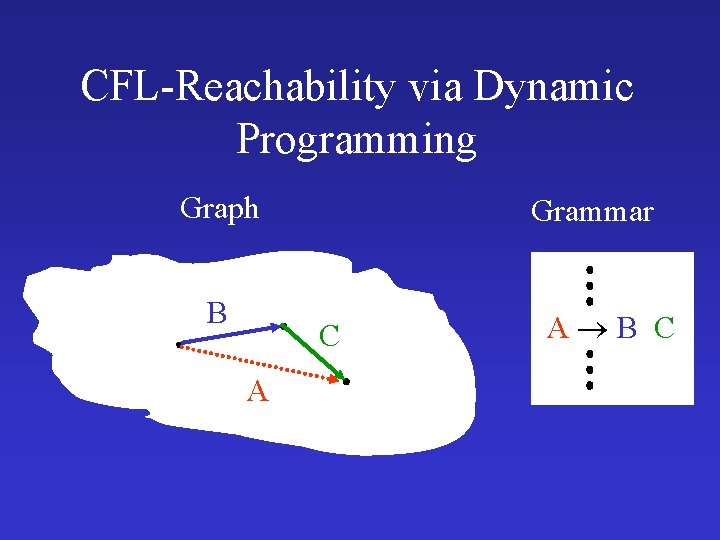
CFL-Reachability via Dynamic Programming Graph B Grammar C A A B C

Dynamic Transitive Closure ? ! • Aiken et al. – Set-constraint solvers – Points-to analysis • Henglein et al. – type inference • But a CFL captures a non-transitive reachability relation [Valiant 75]

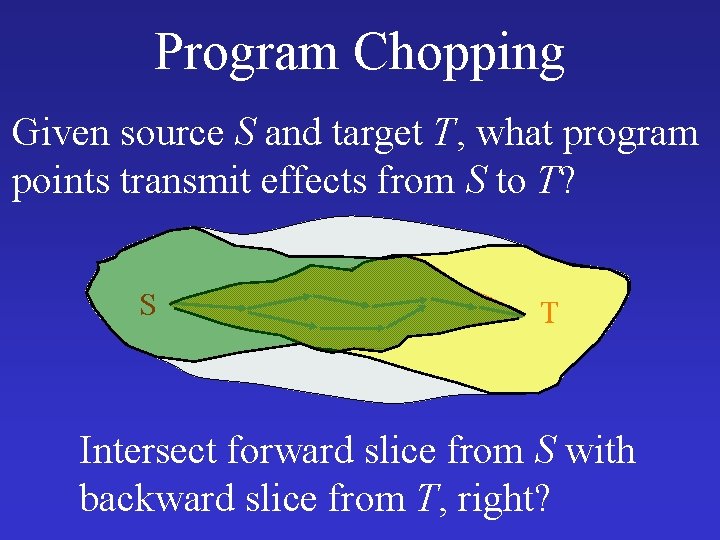
Program Chopping Given source S and target T, what program points transmit effects from S to T? S T Intersect forward slice from S with backward slice from T, right?

Non-Transitivity and Slicing int main() { int add(int x, int y) { int sum = 0; return x + y; int i = 1; } while (i < 11) { sum = add(sum, i); i = add(i, 1); } printf(“%dn”, sum); printf(“%dn”, i); } Forward slice with respect to “sum = 0”

Non-Transitivity and Slicing int main() { int add(int x, int y) { int sum = 0; return x + y; int i = 1; } while (i < 11) { sum = add(sum, i); i = add(i, 1); } printf(“%dn”, sum); printf(“%dn”, i); } Forward slice with respect to “sum = 0”

Non-Transitivity and Slicing int main() { int add(int x, int y) { int sum = 0; return x + y; int i = 1; } while (i < 11) { sum = add(sum, i); i = add(i, 1); } printf(“%dn”, sum); printf(“%dn”, i); } Backward slice with respect to “printf(“%dn”, i)”

Non-Transitivity and Slicing int main() { int add(int x, int y) { int sum = 0; return x + y; int i = 1; } while (i < 11) { sum = add(sum, i); i = add(i, 1); } printf(“%dn”, sum); printf(“%dn”, i); } Backward slice with respect to “printf(“%dn”, i)”

Non-Transitivity and Slicing int main() { int add(int x, int y) { int sum = 0; return x + y; int i = 1; } while (i < 11) { sum = add(sum, i); i = add(i, 1); } printf(“%dn”, sum); printf(“%dn”, i); } Forward slice with respect to “sum = 0” Backward slice with respect to “printf(“%dn”, i)”

Non-Transitivity and Slicing int main() { int add(int x, int y) { int sum = 0; return x + y; int i = 1; } while (i < 11) { sum = add(sum, i); i = add(i, 1); } printf(“%dn”, sum); printf(“%dn”, i); } Chop with respect to “sum = 0” and “printf(“%dn”, i)”

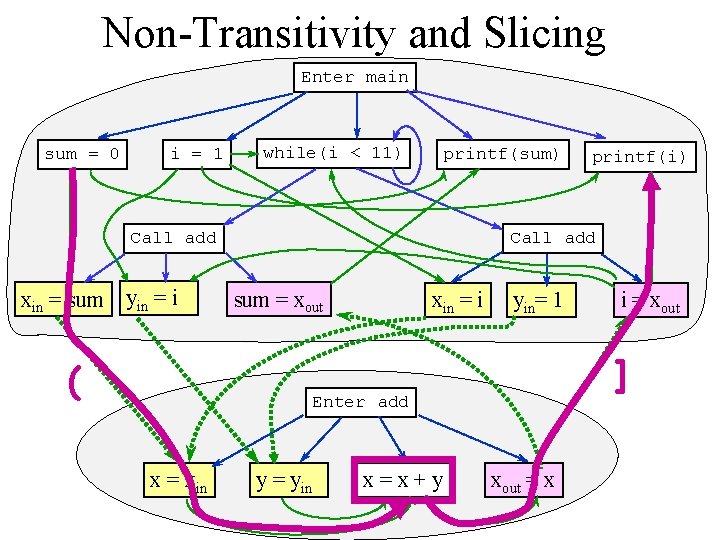
Non-Transitivity and Slicing Enter main sum = 0 i = 1 while(i < 11) printf(sum) Call add xin = sum yin = i ( sum = xout xin = i yin= 1 y = yin x=x+y i = xout ] Enter add x = xin printf(i) xout = x

Program Chopping Given source S and target T, what program points transmit effects from S to T? S T “Precise interprocedural chopping” [Reps & Rosay FSE 95]

CF-Recognition vs. CFL-Reachability • CF-Recognition – Chain graphs – General grammar: sub-cubic time [Valiant 75] – LL(1), LR(1): linear time • CFL-Reachability – General graphs: O(N 3) – LL(1): O(N 3) – LR(1): O(N 3) – Certain kinds of graphs: O(N+E) Gen/kill IDFA GMOD IDFA – Regular languages: O(N+E)

Regular-Language Reachability [Yannakakis 90] • G: Graph (N nodes, E edges) • L: A regular language • L-path from s to t iff • Running time: O(N+E) vs. O(N 3) • Ordinary reachability (= transitive closure) – Label each edge with e – L is e*

Security of Crypto-Based Protocols for Distributed System • “Ping-pong” protocols (1) X —Encrypt. Y(M X) Y (2) Y —Encrypt. X(M) X • [Dolev & Yao 83] – O(N 8) algorithm • [Dolev, Even, & Karp 83] – Less well known than [Dolev & Yao 83] – O(N 3) algorithm

[Dolev, Even, & Karp 83] Id Encrypt. X Id Decrypt. X Id Encrypt. X Id . . . EY Message AX EY Id ? Saboteur AZ

Themes • Harnessing CFL-reachability • Relationship to other analysis paradigms • Exhaustive alg. Demand alg. • Understanding complexity – Linear. . . cubic. . . undecidable • Beyond CFL-reachability

Relationship to Other Analysis Paradigms • Dataflow analysis – reachability versus equation solving • Deduction • Set constraints

Dataflow Analysis • Goal: For each point in the program, determine a superset of the “facts” that could possibly hold during execution • Examples – Constant propagation – Reaching definitions – Live variables – Possibly uninitialized variables

Useful For. . . • • Optimizing compilers Parallelizing compilers Tools that detect possible logical errors Tools that show the effects of a proposed modification

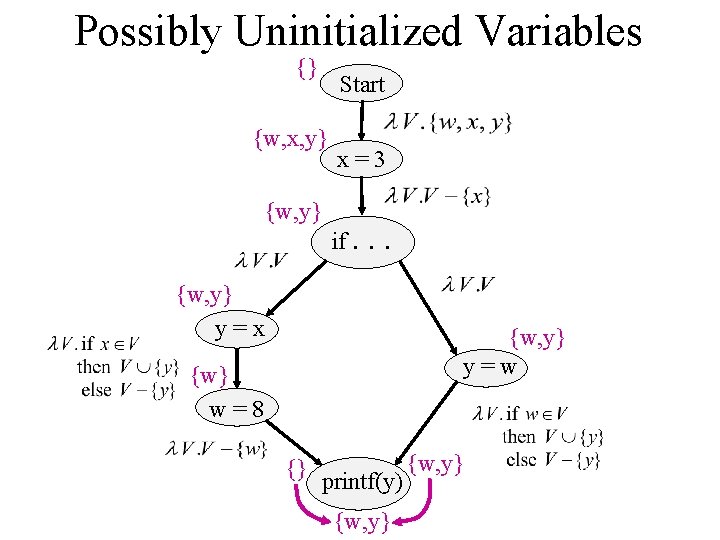
Possibly Uninitialized Variables {} Start {w, x, y} {w, y} x=3 if. . . {w, y} y=x {w, y} y=w {w} w=8 {} printf(y) {w, y}

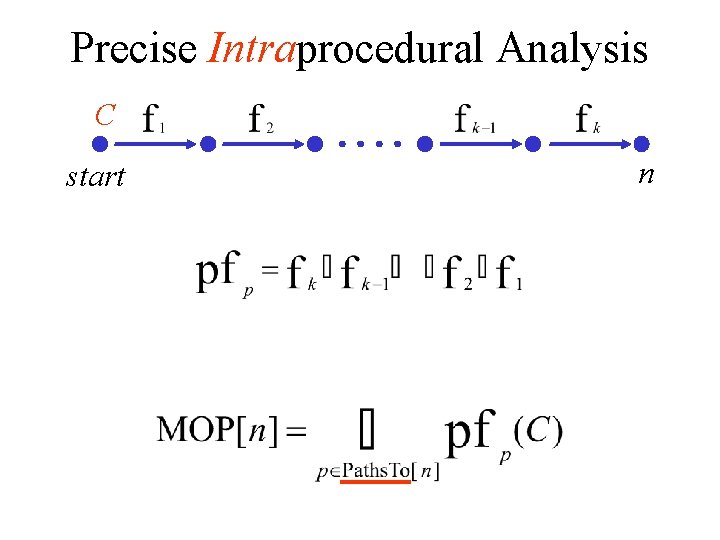
Precise Intraprocedural Analysis C start n

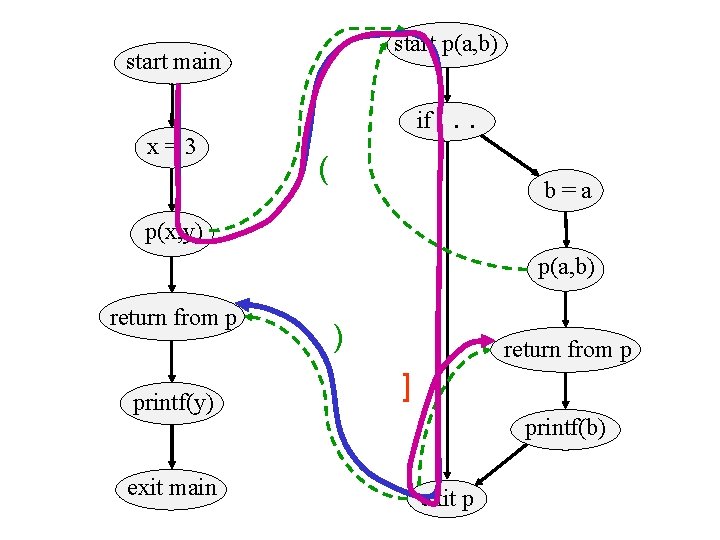
start p(a, b) start main x=3 if. . . ( b=a p(x, y) p(a, b) return from p printf(y) exit main ) return from p ] printf(b) exit p

Precise Interprocedural Analysis ret C start ( ) [Sharir & Pnueli 81] n

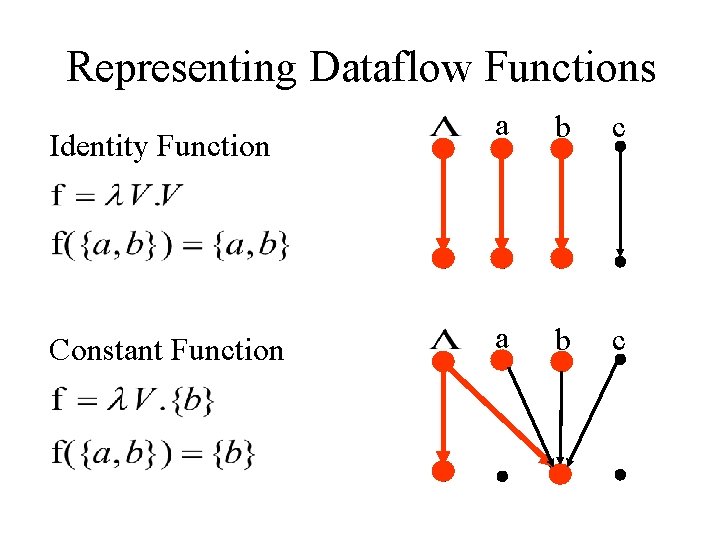
Representing Dataflow Functions Identity Function Constant Function a b c

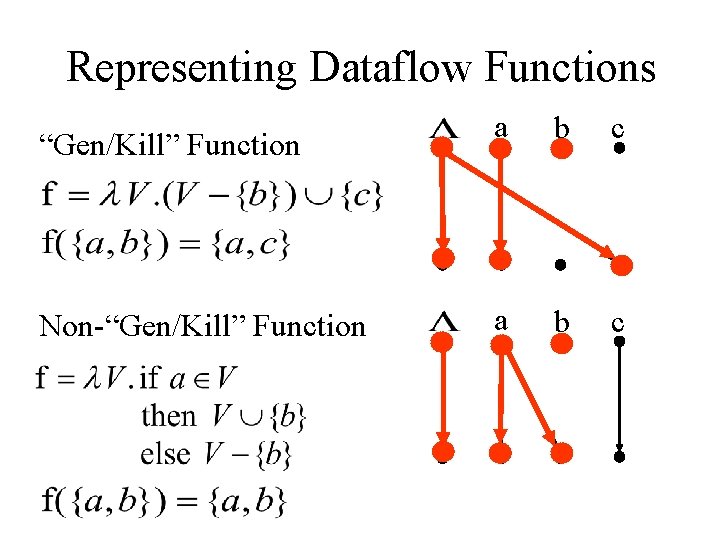
Representing Dataflow Functions “Gen/Kill” Function Non-“Gen/Kill” Function a b c

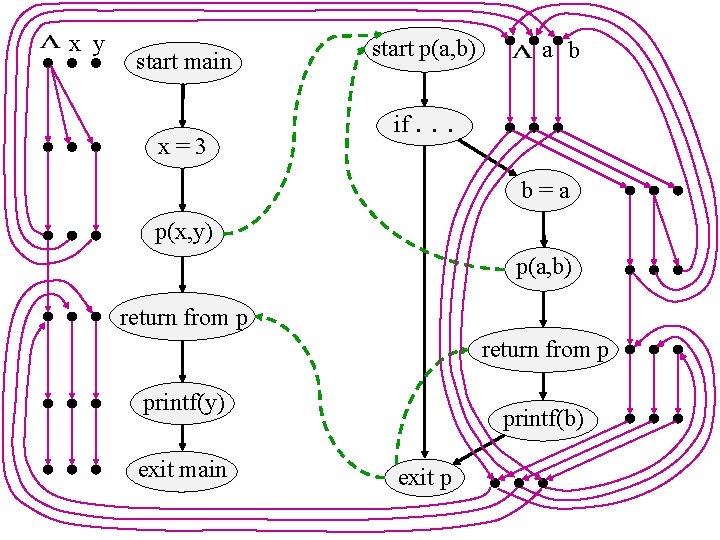
x y start main x=3 start p(a, b) if. a b . . b=a p(x, y) p(a, b) return from p printf(y) exit main printf(b) exit p

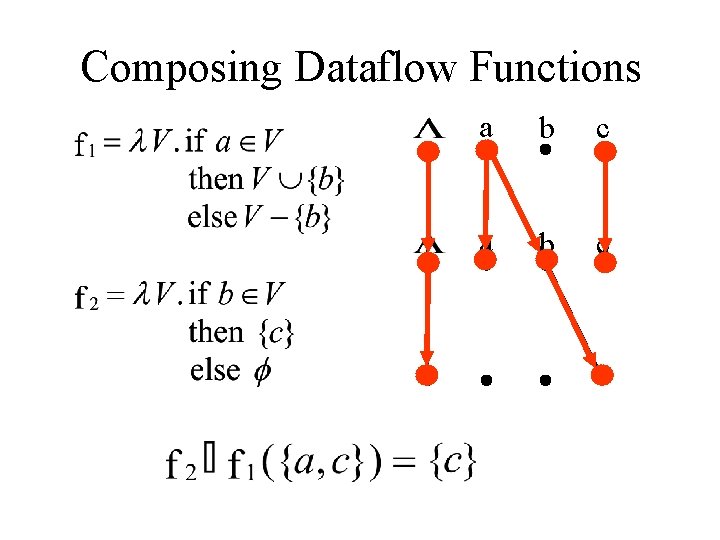
Composing Dataflow Functions a b c

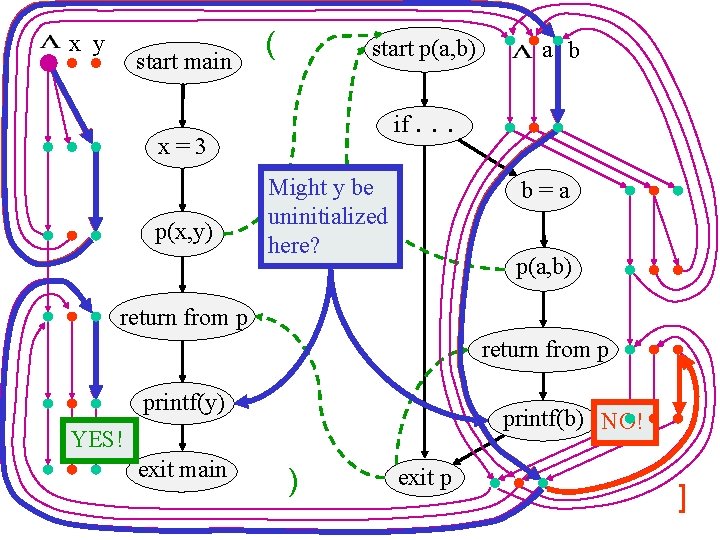
x y start main ( start p(a, b) if. x=3 p(x, y) a b . . Might yb be uninitialized here? b=a p(a, b) return from p printf(y) printf(b) NO! YES! exit main ) exit p ]

matched | | | matched (i matched )i 1 i Call. Sites edge stack Off Limits! ( )( ) ( ( ( ) ) )

unbal. Left | | matched unbal. Left (i unbal. Left 1 i Call. Sites stack Off Limits! ( ) ( ( ( ) ) ( ( )

Interprocedural Dataflow Analysis via CFL-Reachability • Graph: Exploded control-flow graph • L: L(unbal. Left) • Fact d holds at n iff there is an L(unbal. Left)-path from

Asymptotic Running Time [Reps, Horwitz, & Sagiv 95] • CFL-reachability – Exploded control-flow graph: ND nodes – Running time: O(N 3 D 3) • Exploded control-flow graph Special structure Running time: O(ED 3) Typically: E l N, hence O(ED 3) l O(ND 3) “Gen/kill” problems: O(ED)

Why Bother? “We’re only interested in million-line programs” • Know thy enemy! – “Any” algorithm must do these operations – Avoid pitfalls (e. g. , claiming O(N 2) algorithm) • The essence of “context sensitivity” • Special cases – “Gen/kill” problems: O(ED) • Compression techniques – Basic blocks – SSA form, sparse evaluation graphs • Demand algorithms

Relationship to Other Analysis Paradigms • Dataflow analysis – reachability versus equation solving • Deduction • Set constraints

The Need for Pointer Analysis int main() { int add(int x, int y) int sum = 0; { int i = 1; return x + y; int *p = ∑ } int *q = &i; int (*f)(int, int) = add; while (*q < 11) { *p = (*f)(*p, *q); *q = (*f)(*q, 1); } printf(“%dn”, *p); printf(“%dn”, *q); }

The Need for Pointer Analysis int main() { int add(int x, int y) int sum = 0; { int i = 1; return x + y; int *p = ∑ } int *q = &i; int (*f)(int, int) = add; while (*q < 11) { *p = (*f)(*p, *q); *q = (*f)(*q, 1); } printf(“%dn”, *p); printf(“%dn”, *q); }

The Need for Pointer Analysis int main() { int add(int x, int y) int sum = 0; { int i = 1; return x + y; int *p = ∑ } int *q = &i; int (*f)(int, int) = add; while (i < 11) { sum = add(sum, i); i = add(i, 1); } printf(“%dn”, sum); printf(“%dn”, i); }

Flow-Sensitive Points-To Analysis p p s 1 r 2 r 1 s 2 s 3 r 1 r 2 s 2 q q p = &q; p p = *q; p *p = q; p q r 1 r 2 s 1 q r 1 s 2 s 3 r 1 r 2 s 2 q q

Flow-Sensitive Flow-Insensitive start main 1 1 2 5 3 exit main 4 5 2 3 4

Flow-Insensitive Points-To Analysis [Andersen 94, Shapiro & Horwitz 97] p = &q; p p = *q; p *p = q; p q r 1 r 2 s 1 q r 1 s 2 s 3 r 1 r 2 s 2 q q

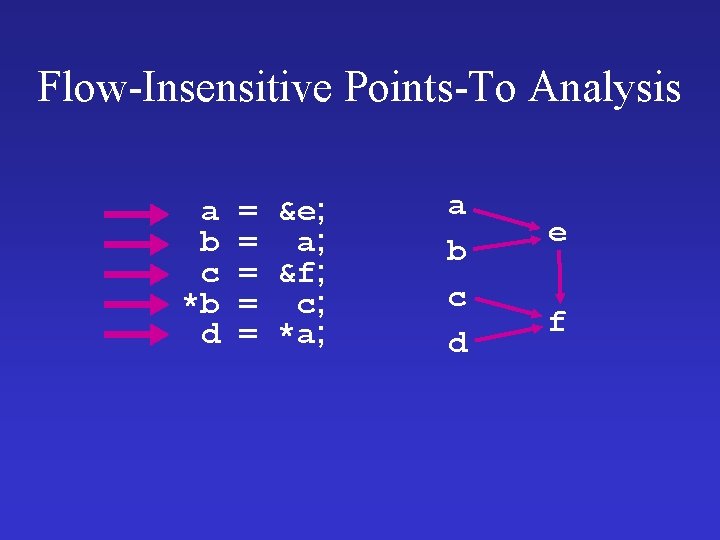
Flow-Insensitive Points-To Analysis a b c *b d = &e; = a; = &f; = c; = *a; a b c d e f

Flow-Insensitive Points-To Analysis • Andersen [Thesis 94[ – Formulated using set constraints – Cubic-time algorithm • Shapiro & Horwitz (1995; [POPL 97]) – Re-formulated as a graph-grammar problem • Reps (1995; [unpublished]) – Re-formulated as a Horn-clause program • Melski (1996; see [Reps, IST 98]) – Re-formulated via CFL-reachability

CFL-Reachability via Dynamic Programming Graph B Grammar C A A B C

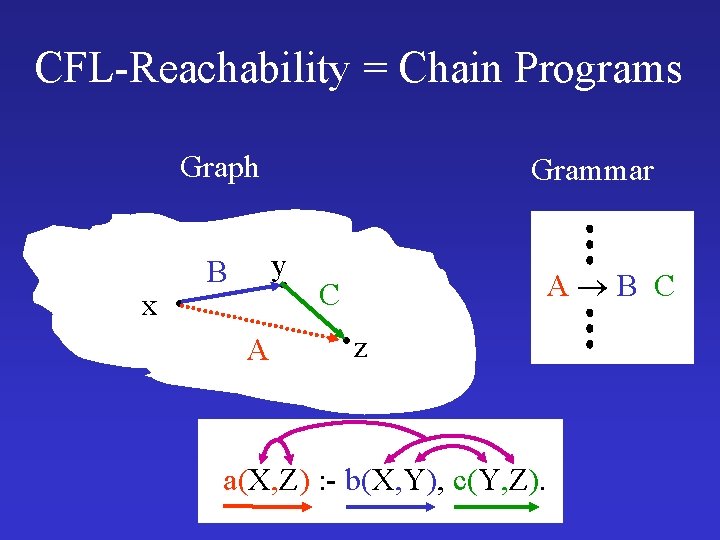
CFL-Reachability = Chain Programs Graph x Grammar y B A A B C C z a(X, Z) : - b(X, Y), c(Y, Z).

Base Facts for Points-To Analysis p = &q; assign. Addr(p, q). p = q; assign(p, q). p = *q; assign. Star(p, q). *p = q; star. Assign(p, q).

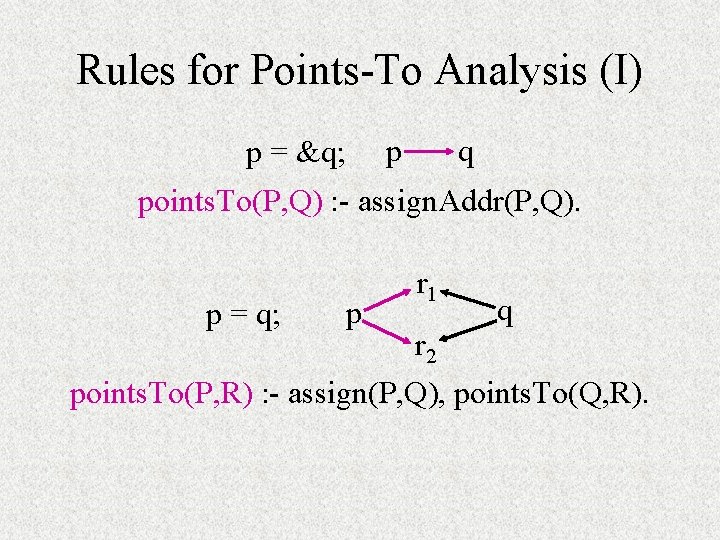
Rules for Points-To Analysis (I) p = &q; p q points. To(P, Q) : - assign. Addr(P, Q). p = q; p r 1 r 2 q points. To(P, R) : - assign(P, Q), points. To(Q, R).

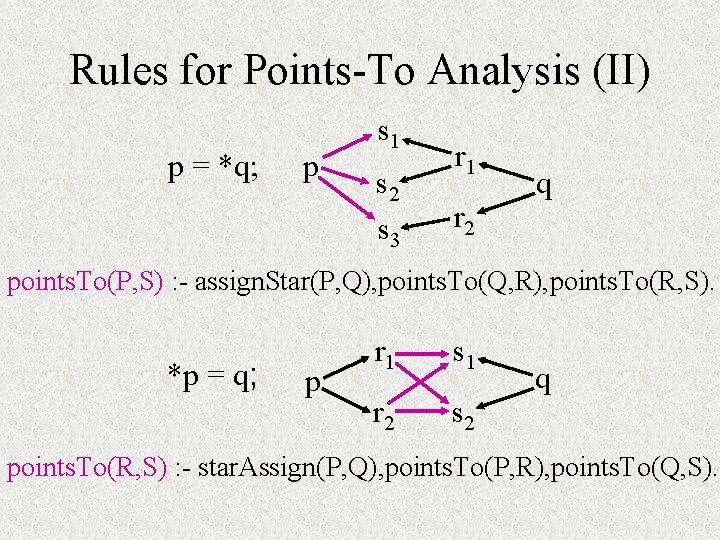
Rules for Points-To Analysis (II) p = *q; p s 1 s 2 s 3 r 1 r 2 q points. To(P, S) : - assign. Star(P, Q), points. To(Q, R), points. To(R, S). *p = q; p r 1 s 1 r 2 s 2 q points. To(R, S) : - star. Assign(P, Q), points. To(P, R), points. To(Q, S).

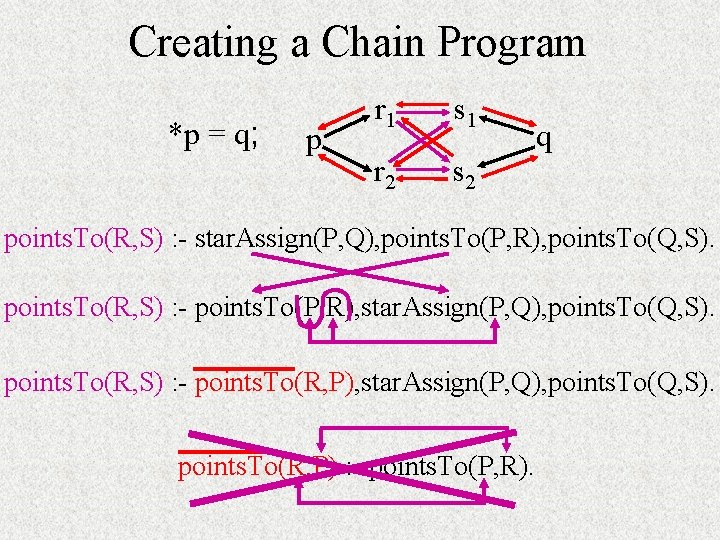
Creating a Chain Program *p = q; p r 1 s 1 r 2 s 2 q points. To(R, S) : - star. Assign(P, Q), points. To(P, R), points. To(Q, S). points. To(R, S) : - points. To(P, R), star. Assign(P, Q), points. To(Q, S). points. To(R, S) : - points. To(R, P), star. Assign(P, Q), points. To(Q, S). points. To(R, P) : - points. To(P, R).

Base Facts for Points-To Analysis p = &q; assign. Addr(p, q). assign. Addr(q, p). p = q; assign(p, q). assign(q, p). p = *q; assign. Star(p, q). assign. Star(q, p). *p = q; star. Assign(p, q). star. Assign(q, p).

Creating a Chain Program points. To(P, Q) : - assign. Addr(P, Q). points. To(Q, P) : - assign. Addr(Q, P). points. To(P, R) : - assign(P, Q), points. To(Q, R). points. To(R, P) : - points. To(R, Q), assign(Q, P). points. To(P, S) : - assign. Star(P, Q), points. To(Q, R), points. To(R, S). points. To(S, P) : - points. To(S, R), points. To(R, Q), assign. Star(Q, P). points. To(R, S) : - points. To(R, P), star. Assign(P, Q), points. To(Q, S). points. To(S, R) : - points. To(S, Q), star. Assign(Q, P), points. To(P, R).

. . . and now to CFL-Reachability points. To assign. Addr points. To assign points. To assign points. To assign. Star points. To assign. Star points. To star. Assign points. To

Relationship to Other Analysis Paradigms • Dataflow analysis – reachability versus equation solving • Deduction • Set constraints

1987 1993 1994 1995 1996 1997 1998 Slicing & Applications Dataflow Analysis Demand CFL Algorithms Reachability Structure. Transmitted Dependences Set Constraints

Structure-Transmitted Dependences [Reps 1995] Mc. Carthy’s equations: car(cons(x, y)) = x cdr(cons(x, y)) = y w = cons(x, y); v = car(w); x y w v

Set Constraints w = cons(x, y); v = car(w); Mc. Carthy’s Equations Revisited Semantics of Set Constraints

CFL-Reachability versus Set Constraints • Lazy languages: CFL-reachability is more natural – car(cons(X, Y)) = X • Strict languages: Set constraints are more natural – car(cons(X, Y)) = X, provided I(Y) g v • But. . . SC and CFL-reachability are equivalent! – [Melski & Reps 97]

Solving Set Constraints W is “inhabited” X is “inhabited” Y is “inhabited” X is “inhabited” W is “inhabited”

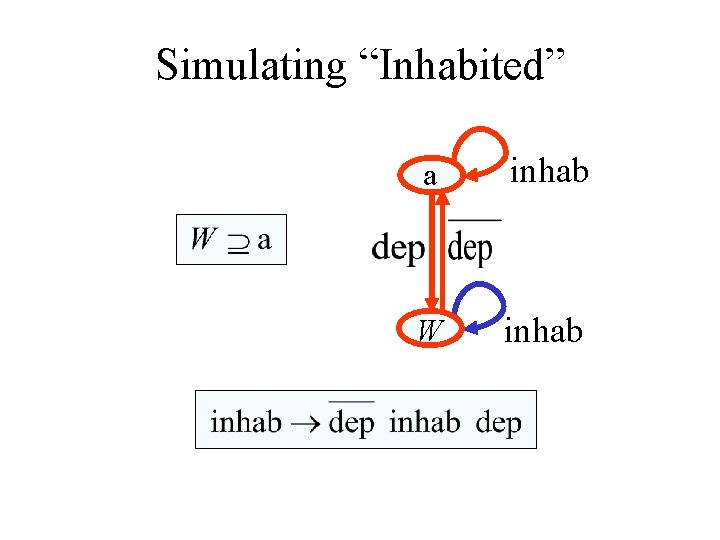
Simulating “Inhabited” a inhab W inhab

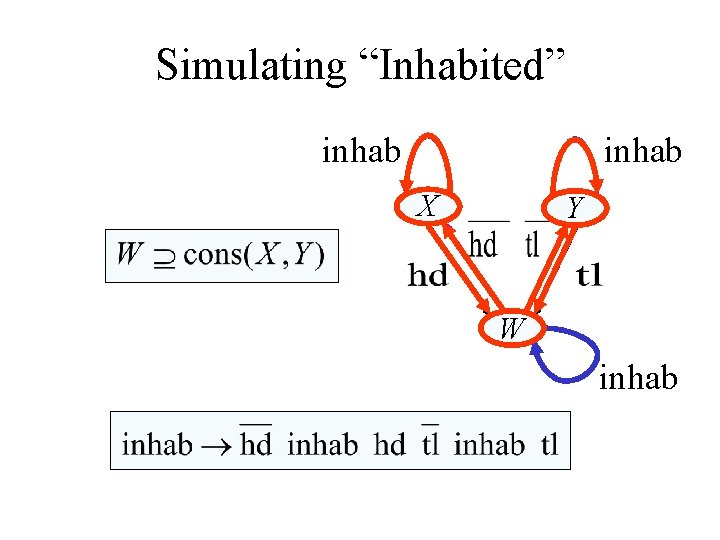
Simulating “Inhabited” inhab X Y W inhab

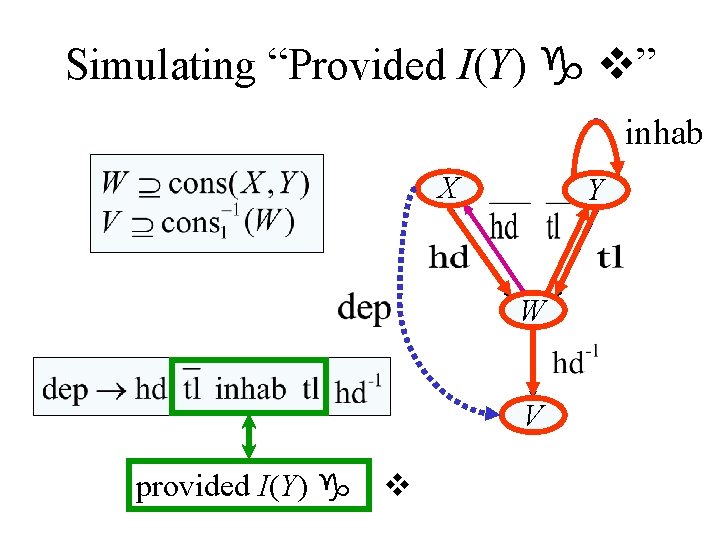
Simulating “Provided I(Y) g v” inhab X Y W V provided I(Y) g v

Themes • Harnessing CFL-reachability • Relationship to other analysis paradigms • Exhaustive alg. Demand alg. • Understanding complexity – Linear. . . cubic. . . undecidable • Beyond CFL-reachability

Exhaustive Versus Demand Analysis • Exhaustive analysis: All facts at all points • Optimization: Concentrate on inner loops • Program-understanding tools: Only some facts are of interest

Exhaustive Versus Demand Analysis • Demand analysis: – Does a given fact hold at a given point? – Which facts hold at a given point? – At which points does a given fact hold? • Demand analysis via CFL-reachability – single-source/single-target CFL-reachability – single-source/multi-target CFL-reachability – multi-source/single-target CFL-reachability

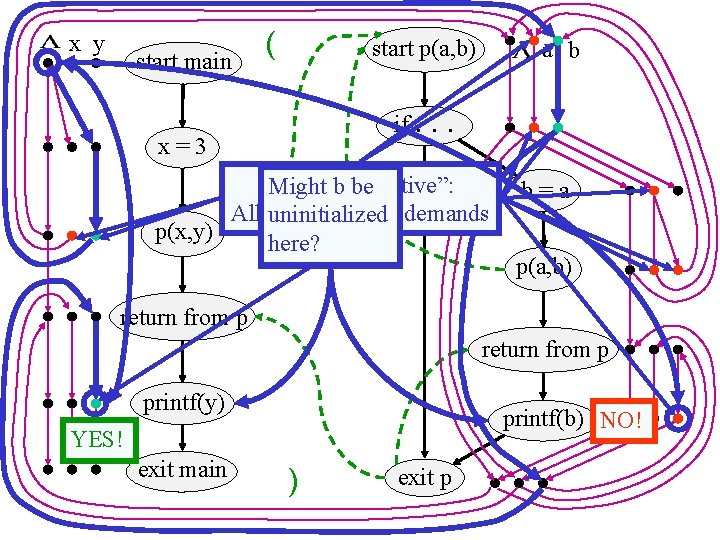
x y start main ( start p(a, b) if. x=3 a b . . “Semi-exhaustive”: Might by be All “appropriate” uninitialized demands p(x, y) here? b=a p(a, b) return from p printf(y) printf(b) NO! YES! exit main ) exit p

Experimental Results [Horwitz , Reps, & Sagiv 1995] • 53 C programs (200 -6, 700 lines) • For a single fact of interest: – demand always better than exhaustive • All “appropriate” demands beats exhaustive when percentage of “yes” answers is high – Live variables – Truly live variables – Constant predicates –. . .

A Related Result [Sagiv, Reps, & Horwitz 1996] • ]Uses a generalized analysis technique[ • 38 C programs (300 -6, 000 lines( – copy-constant propagation – linear-constant propagation • All “appropriate” demands always beats exhaustive – factor of 1. 14 to about 6

Exhaustive Versus Demand Analysis • Demand algorithms for – Interprocedural dataflow analysis – Set constraints – Points-to analysis

Demand Analysis and LP Queries (I) • Flow-insensitive points-to analysis – Does variable p point to q? • Issue query: ? - points. To(p, q). • Solve single-source/single-target L(points. To)reachability problem – What does variable p point to? • Issue query: ? - points. To(p, Q). • Solve single-source L(points. To)-reachability problem – What variables point to q? • Issue query: ? - points. To(P, q). • Solve single-target L(points. To)-reachability problem

Demand Analysis and LP Queries (II) • Flow-sensitive analysis – Does a given fact f hold at a given point p? ? - df. Fact(p, f). – Which facts hold at a given point p? ? - df. Fact(p, F). – At which points does a given fact f hold? ? - df. Fact(P, f). • E. g. , flow-sensitive points-to analysis ? - df. Fact(p, points. To(x, Y)). ? - df. Fact(P, points. To(x, y)). etc.

Themes • Harnessing CFL-reachability • Relationship to other analysis paradigms • Exhaustive alg. Demand alg. • Understanding complexity – Linear. . . cubic. . . undecidable • Beyond CFL-reachability

Interprocedural Backward Slice Enter main Call p ) ( [ ] Enter p

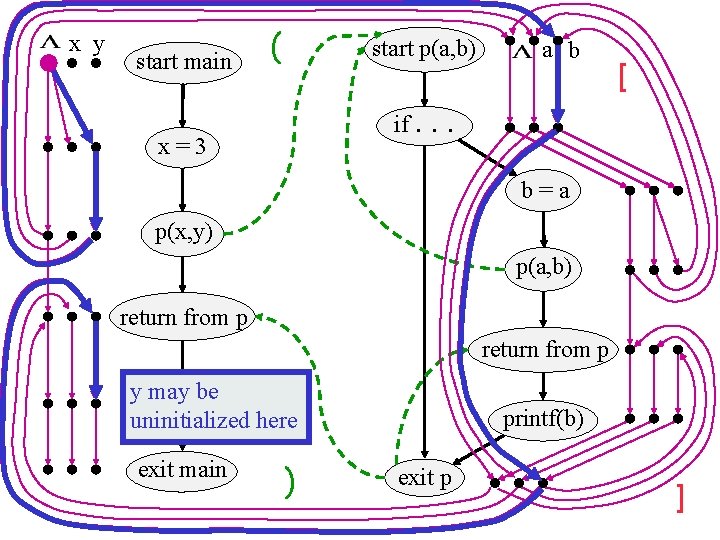
x y start main ( start p(a, b) if. x=3 a b [ . . b=a p(x, y) p(a, b) return from p y printf(y) may be uninitialized here exit main ) printf(b) exit p ]

Structure-Transmitted Dependences [Reps 1995] Mc. Carthy’s equations: car(cons(x, y)) = x cdr(cons(x, y)) = y w = cons(x, y); v = car(w); x y w v

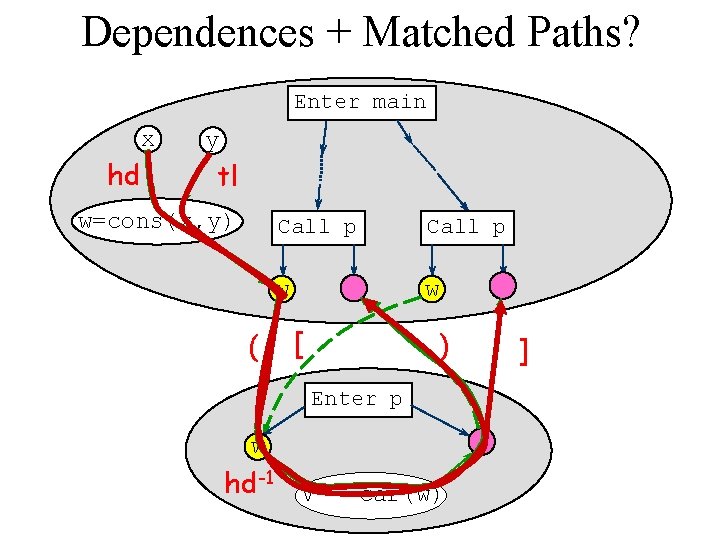
Dependences + Matched Paths? Enter main x hd y tl w=cons(x, y) ( Call p w w [ ) Enter p w hd-1 v = car(w) ]

Undecidable! [Reps, TOPLAS 00] hd ( hd-1 Interleaved Parentheses! )

Themes • Harnessing CFL-reachability • Relationship to other analysis paradigms • Exhaustive alg. Demand alg. • Understanding complexity – Linear. . . cubic. . . undecidable • Beyond CFL-reachability

CFL-Reachability via Dynamic Programming Graph B Grammar C A A B C

Beyond CFL-Reachability: Composition of Linear Functions x. 3 x+5 x. 2 x+1 x. 6 x+11 ( x. 2 x+1) ( x. 3 x+5) = x. 6 x+11

Beyond CFL-Reachability: Composition of Linear Functions • Interprocedural constant propagation – [Sagiv, Reps, & Horwitz TCS 96] • Interprocedural path profiling – The number of path fragments contributed by a procedure is a function – [Melski & Reps CC 99]

Model-Checking of Recursive HFSMs [Benedikt, Godefroid, & Reps (in prep. )] • Non-recursive HFSMs [Alur & Yannakakis 98] • Ordinary FSMs – T-reachability/circularity queries • Recursive HFSMs – Matched-parenthesis T-reachability/circularity • Key observation: Linear-time algorithms for matched-parenthesis T-reachability/cyclicity – Single-entry/multi-exit [or multi-entry/single-exit] – Deterministic, multi-entry/multi-exit

T-Cyclicity in Hierarchical Kripke Structures SN/SX MN/SX non-rec: O(|k|) ? rec: O(|k|3) rec: ? SN/SX O(|k|) SN/MX O(|k|) MN/SX O(|k|) MN/MX ? MN/MX O(|k|3) O(|k||t|) [lin rec] O(|k|) [det]

Recursive HFSMs: Data Complexity SN/SX SN/MX MN/SX LTL non-rec: O(|k|) ? rec: P-time rec: ? MN/MX ? CTL O(|k|) bad CTL* O(|k|2) [L 2] bad bad ? ?

Recursive HFSMs: Data Complexity SN/SX LTL O(|k|) SN/MX O(|k|) MN/SX O(|k|) CTL* O(|k|) bad O(|k|) Not Dual Problems! MN/MX O(|k|3) O(|k||t|) [lin rec] O(|k|) [det] bad

CFL-Reachability: Scope of Applicability • Static analysis – Slicing, DFA, structure-transmitted dep. , points-to analysis • Verification – Security of crypto-based protocols for distributed systems [Dolev, Even, & Karp 83] – Model-checking recursive HFSMs • Formal-language theory – CF-, 2 DPDA-, 2 NPDA-recognition – Attribute-grammar analysis

CFL-Reachability: Benefits • Algorithms – Exhaustive & demand • Complexity – Linear-time and cubic-time algorithms – PTIME-completeness – Variants that are undecidable • Complementary to – Equations – Set constraints – Types –. . .

Most Significant Contributions: 1987 -2000 • Asymptotically fastest algorithms – Interprocedural slicing – Interprocedural dataflow analysis • Demand algorithms – Interprocedural dataflow analysis [CC 94, FSE 95] – All “appropriate” demands beats exhaustive • Tool for slicing and browsing ANSI C – Slices programs as large as 75, 000 lines – University research distribution – Commercial product: Code. Surfer (Gramma. Tech, Inc. )

Most Significant Contributions: 1987 -2000 • Unifying conceptual model – [Kou 77], [Holley&Rosen 81], [Cooper&Kennedy 88], [Callahan 88], [Horwitz, Reps, &Binkley 88], . . . • Identifies fundamental bottlenecks – Cubic-time “barrier” – Litmus test: quadratic-time algorithm? ! – PTIME-complete limits to parallelizability • Existence proofs for new algorithms – Demand algorithm for set constraints – Demand algorithm for points-to analysis

References • Papers by Reps and collaborators: – http: //www. cs. wisc. edu/~reps/ • CFL-reachability – Yannakakis, M. , Graph-theoretic methods in database theory, PODS 90. – Reps, T. , Program analysis via graph reachability, Inf. and Softw. Tech. 98.

References • Slicing, chopping, etc. – Horwitz, Reps, & Binkley, TOPLAS 90 – Reps, Horwitz, Sagiv, & Rosay, FSE 94 – Reps & Rosay, FSE 95 • Dataflow analysis – Reps, Horwitz, & Sagiv, POPL 95 – Horwitz, Reps, & Sagiv, FSE 95, TR-1283 • Structure dependences; set constraints – Reps, PEPM 95 – Melski & Reps, Theor. Comp. Sci. 00

References • Complexity – Undecidability: Reps, TOPLAS 00? – PTIME-completeness: Reps, Acta Inf. 96. • Verification – Dolev, Even, & Karp, Inf & Control 82. – Benedikt, Godefroid, & Reps, In prep. • Beyond CFL-reachability – Sagiv, Reps, Horwitz, Theor. Comp. Sci 96 – Melski & Reps, CC 99, TR-1382