Profiling the Pulse of Scientific Fronts Balanced Binary

搜集 · 评估 · 分析 · 决策 Profiling the Pulse of Scientific Fronts Balanced Binary Search Trees 胡智文 | 博士 & 教授 浙江 商大学 计算机与信息 程学院 手机: 13676458899 邮箱:huzhiwen@zjgsu. edu. cn 网址:http: //zhiwenhu. hustoj. com/ 地址:中国 · 浙江 · 杭州 下沙高教园区学正街 18号

Objectives p. To know what an AVL tree is (§ 26. 1). p. To understand how to rebalance a tree using the LL rotation, LR rotation, RR rotation, and RL rotation (§ 26. 2). p. To know how to design the AVLTree class (§ 26. 3). p. To insert elements into an AVL tree (§ 26. 4). p. To implement node rebalancing (§ 26. 5). p. To delete elements from an AVL tree (§ 26. 6). p. To implement the AVLTree class (§ 26. 7). p. To test the AVLTree class (§ 26. 8). p. To analyze the complexity of search, insert, and delete operations in AVL trees (§ 26. 9). Data Structures 2
Agenda 提纲 01 Introduction 02 03 04 05 Rebalancing Trees The AVLTree class Chapter Summary Brainstorm
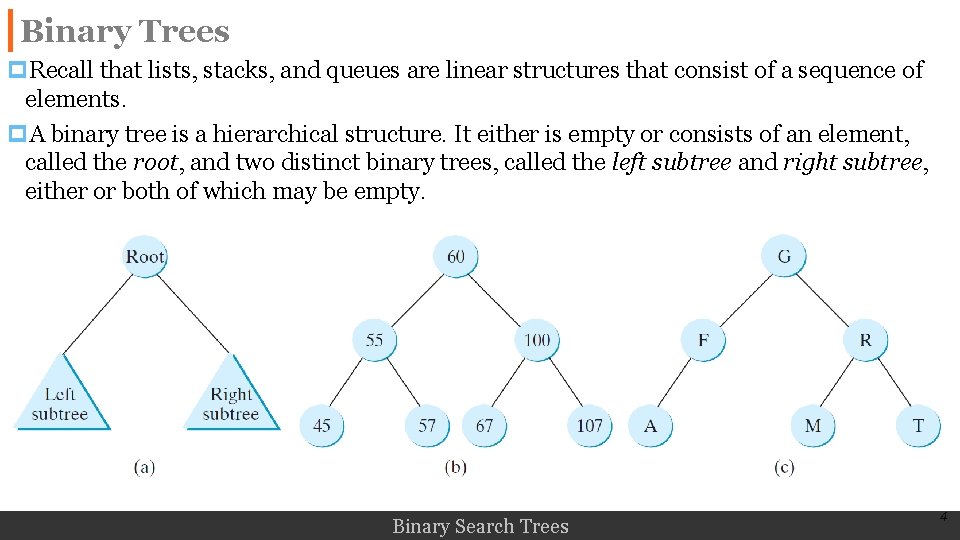
Binary Trees p. Recall that lists, stacks, and queues are linear structures that consist of a sequence of elements. p. A binary tree is a hierarchical structure. It either is empty or consists of an element, called the root, and two distinct binary trees, called the left subtree and right subtree, either or both of which may be empty. Binary Search Trees 4
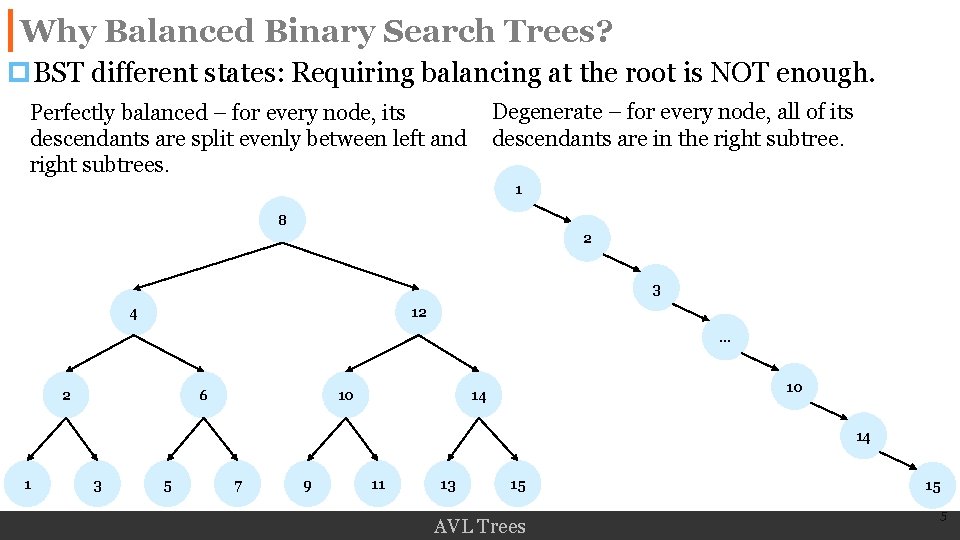
Why Balanced Binary Search Trees? p. BST different states: Requiring balancing at the root is NOT enough. Degenerate – for every node, all of its descendants are in the right subtree. Perfectly balanced – for every node, its descendants are split evenly between left and right subtrees. 1 8 2 3 4 12 … 2 6 10 10 14 14 1 3 5 7 9 11 13 15 AVL Trees 15 5

Why Balanced Binary Search Trees? p. The search, insertion, and deletion times for a binary tree depend on the height of the tree. In the worst case, the height is O(n). p. If a tree is perfectly balanced—that is, a complete binary tree—its height is log n. p. Can we maintain a perfectly balanced tree? Yes, but doing so will be costly. p. The compromise is to maintain a well-balanced tree—that is, the heights of every node’s two subtrees are about the same. Right subtree HL Left subtree bt Height=max(HL, HR)+1 HR AVL Trees 6

What is an AVL Tree? p. AVL trees were invented in 1962 by two Russian computer scientists, G. M. Adelson. Velsky and E. M. Landis (hence the name AVL). Гео ргий Макси мович Адельсо н-Ве льский Евгений Михайлович Ландис (8 January 1922~) Russian (1921. 10. 6~1997. 12) Russian Adelson-Velskii, G. ; E. M. Landis (1962). An algorithm for the organization of information. Proceedings of the USSR Academy of Sciences 146: 263 -266. 7
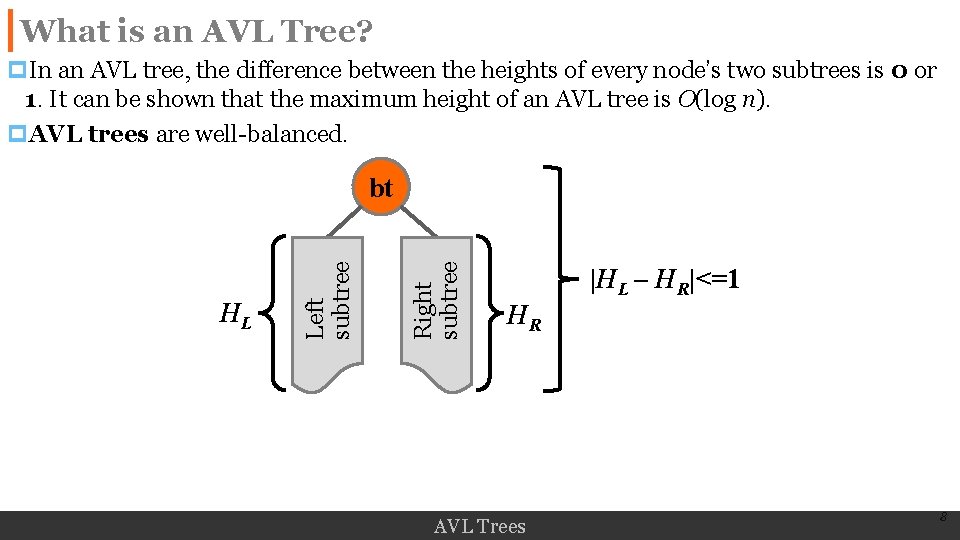
What is an AVL Tree? p. In an AVL tree, the difference between the heights of every node’s two subtrees is 0 or 1. It can be shown that the maximum height of an AVL tree is O(log n). p. AVL trees are well-balanced. Right subtree HL Left subtree bt |HL – HR|<=1 HR AVL Trees 8
Agenda 提纲 01 Introduction 02 03 04 05 Rebalancing Trees The AVLTree class Chapter Summary Brainstorm
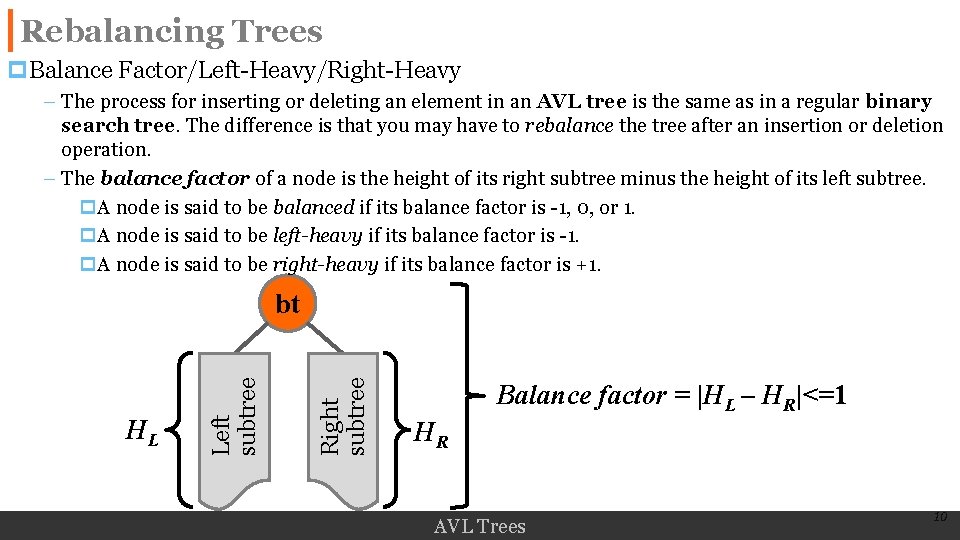
Rebalancing Trees p. Balance Factor/Left-Heavy/Right-Heavy – The process for inserting or deleting an element in an AVL tree is the same as in a regular binary search tree. The difference is that you may have to rebalance the tree after an insertion or deletion operation. – The balance factor of a node is the height of its right subtree minus the height of its left subtree. p. A node is said to be balanced if its balance factor is -1, 0, or 1. p. A node is said to be left-heavy if its balance factor is -1. p. A node is said to be right-heavy if its balance factor is +1. Right subtree HL Left subtree bt Balance factor = |HL – HR|<=1 HR AVL Trees 10
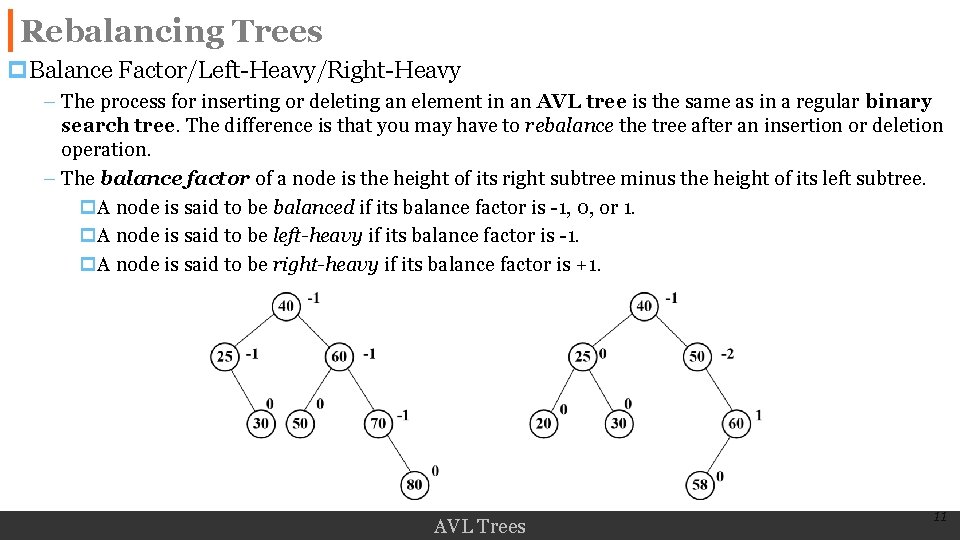
Rebalancing Trees p. Balance Factor/Left-Heavy/Right-Heavy – The process for inserting or deleting an element in an AVL tree is the same as in a regular binary search tree. The difference is that you may have to rebalance the tree after an insertion or deletion operation. – The balance factor of a node is the height of its right subtree minus the height of its left subtree. p. A node is said to be balanced if its balance factor is -1, 0, or 1. p. A node is said to be left-heavy if its balance factor is -1. p. A node is said to be right-heavy if its balance factor is +1. AVL Trees 11
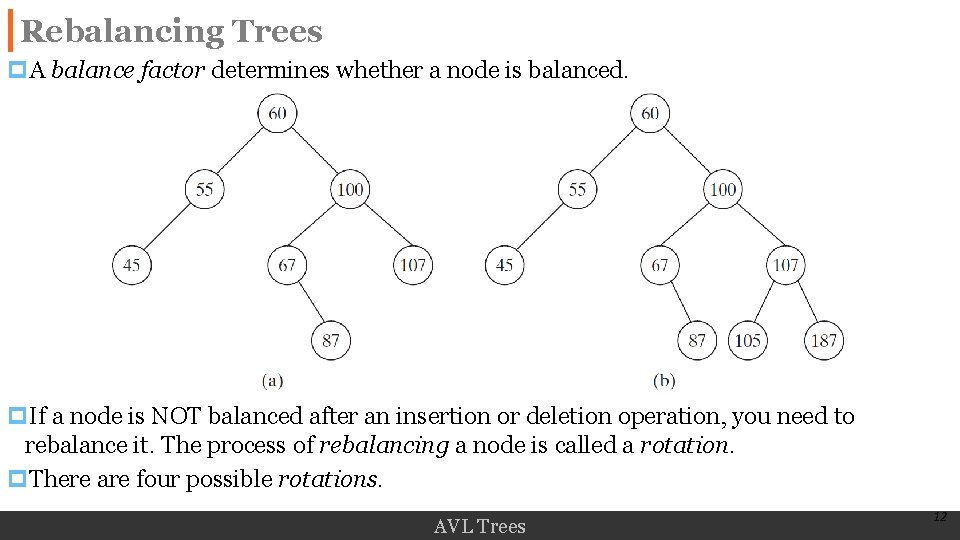
Rebalancing Trees p. A balance factor determines whether a node is balanced. p. If a node is NOT balanced after an insertion or deletion operation, you need to rebalance it. The process of rebalancing a node is called a rotation. p. There are four possible rotations. AVL Trees 12

Rebalancing Trees AVL Trees 13
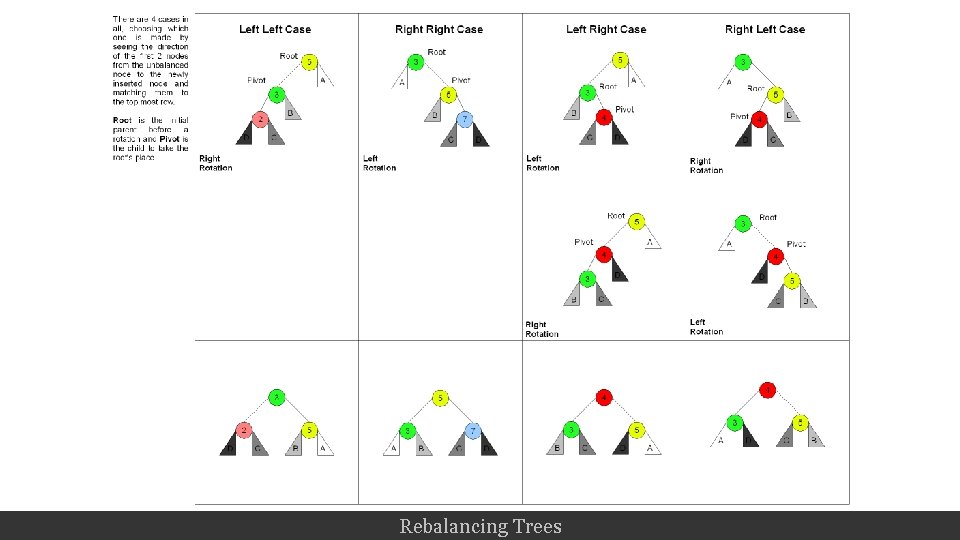
Rebalancing Trees
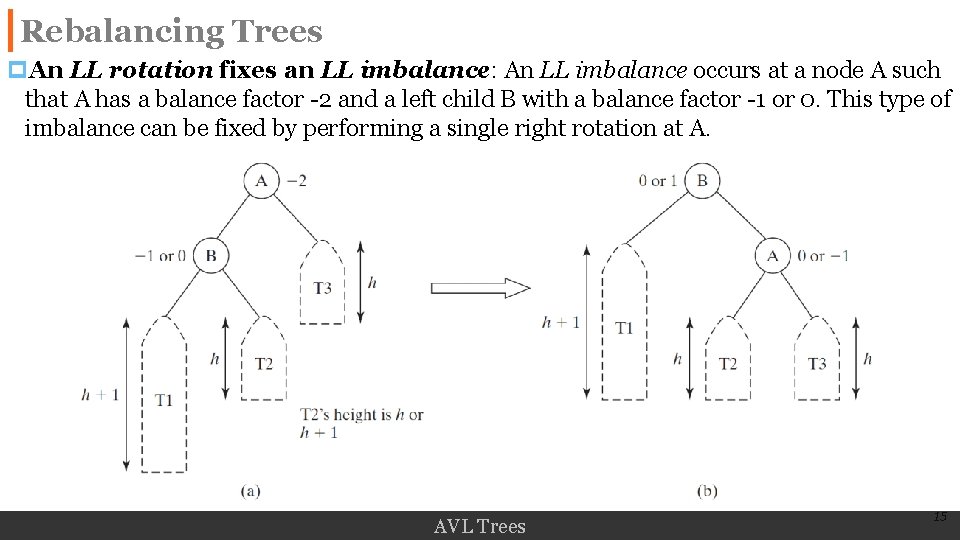
Rebalancing Trees p. An LL rotation fixes an LL imbalance: An LL imbalance occurs at a node A such that A has a balance factor -2 and a left child B with a balance factor -1 or 0. This type of imbalance can be fixed by performing a single right rotation at A. AVL Trees 15
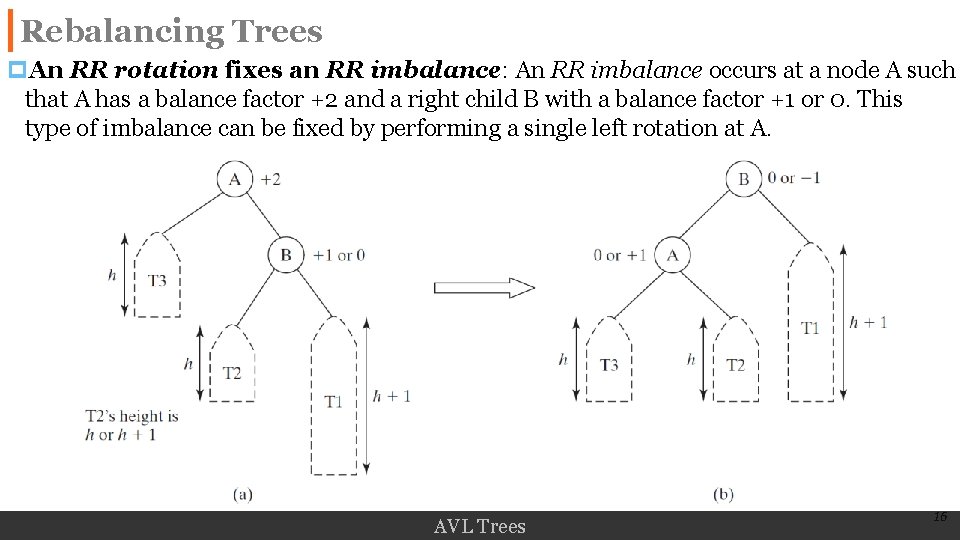
Rebalancing Trees p. An RR rotation fixes an RR imbalance: An RR imbalance occurs at a node A such that A has a balance factor +2 and a right child B with a balance factor +1 or 0. This type of imbalance can be fixed by performing a single left rotation at A. AVL Trees 16
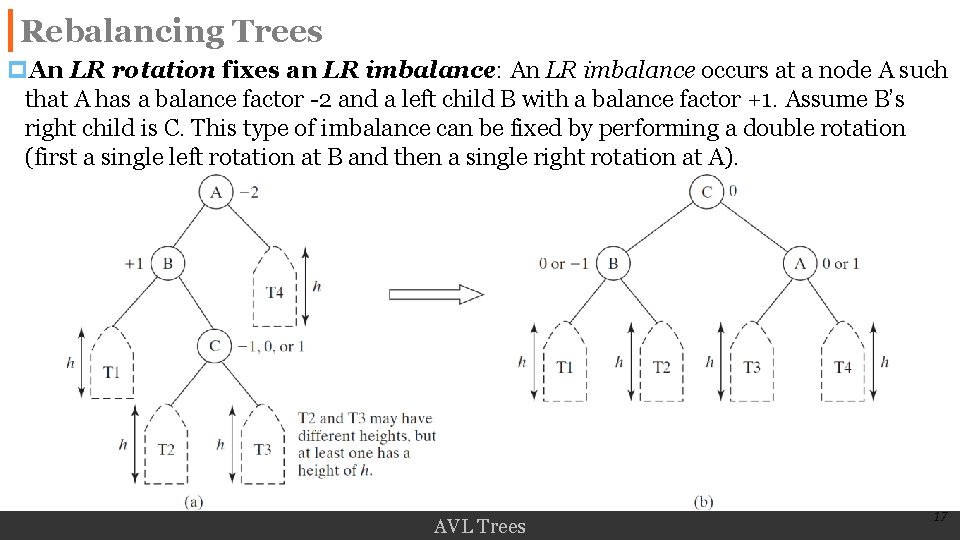
Rebalancing Trees p. An LR rotation fixes an LR imbalance: An LR imbalance occurs at a node A such that A has a balance factor -2 and a left child B with a balance factor +1. Assume B’s right child is C. This type of imbalance can be fixed by performing a double rotation (first a single left rotation at B and then a single right rotation at A). AVL Trees 17
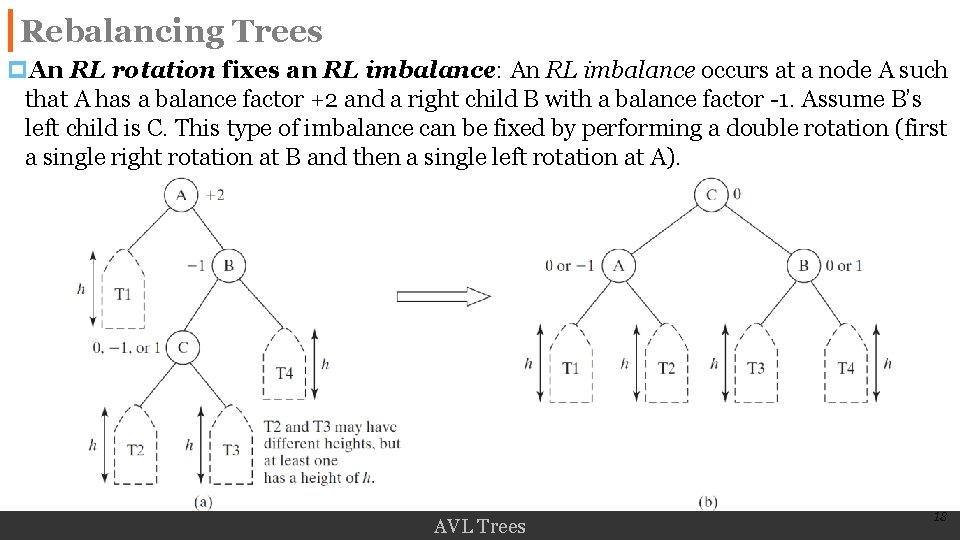
Rebalancing Trees p. An RL rotation fixes an RL imbalance: An RL imbalance occurs at a node A such that A has a balance factor +2 and a right child B with a balance factor -1. Assume B’s left child is C. This type of imbalance can be fixed by performing a double rotation (first a single right rotation at B and then a single left rotation at A). AVL Trees 18
Agenda 提纲 01 Introduction 02 03 04 05 Rebalancing Trees The AVLTree class Chapter Summary Brainstorm

Designing Classes for AVL Trees p. An AVL tree is a binary tree. So you can define the AVLTree class to extend the BST class. AVL Trees 20

Designing Classes for AVL Trees p. In order to balance the tree, you need to know each node’s height. – For convenience, store the height of each node in AVLTree. Node and define AVLTree. Node to be a subclass of BST. Tree. Node. – Note that Tree. Node is defined as a static inner class in BST. AVLTree. Node will be defined as a static inner class in AVLTree. Node contains the data fields element, left, and right, which are inherited by AVLTree. Node. p. An AVLTree. Node contains the protected data fields element, height, left, and right. AVL Trees 21

Overriding the insert Method p. Inserting an element into an AVL tree is the same as inserting it to a BST, except that the tree may need to be rebalanced. p. A new element is always inserted as a leaf node. As a result of adding a new node, the heights of the new leaf node’s ancestors may increase. p. After inserting a new node, check the nodes along the path from the new leaf node up to the root. If an unbalanced node is found, perform an appropriate rotation using the algorithm. p. The algorithm considers each node in the path from the new leaf node to the root. Update the height of the node on the path. If a node is balanced, no action is needed. If a node is NOT balanced, perform an appropriate rotation. AVL Trees 22

Overriding the insert Method p. Inserting an element into an AVL tree is the same as inserting it to a BST, except that the tree may need to be rebalanced. AVL Trees 23

Implementing Rotations p. An unbalanced tree becomes balanced by performing an appropriate rotation operation. p. Here, we give the algorithm for the LL rotation: p. Note the height of nodes A and B can be changed, but the heights of other nodes in the tree are NOT changed. You can implement the RR, LR, and RL rotations in a similar manner. AVL Trees 24

Implementing the delete Method p. Deleting an element from an AVL tree is the same as deleting it from a BST, except that the tree may need to be rebalanced. Deleting Elements from a BST, to delete an element from a binary tree, the algorithm first locates the node that contains the element. Let current point to the node that contains the element in the binary tree and parent point to the parent of the current node. The current node may be a left child or a right child of the parent node. p. Two cases arise when deleting an element: – Case 1: The current node does NOT have a left child. p. To delete the current node, simply connect the parent node with the right child of the current node. p. The height of the nodes along the path from the parent node up to the root may have decreased. AVL Trees 25

Implementing the delete Method – Case 2: The current node has a left child. p. Let right. Most point to the node that contains the largest element in the left subtree of the current node and parent. Of. Right. Most point to the parent node of the right. Most node. p. The right. Most node cannot have a right child, but may have a left child. p. Replace the element value in the current node with the one in the right. Most node, connect the parent. Of. Right. Most node with the left child of the right. Most node, and delete the right. Most node. p. The height of the nodes along the path from parent. Of. Right. Most up to the root may have decreased. AVL Trees 26
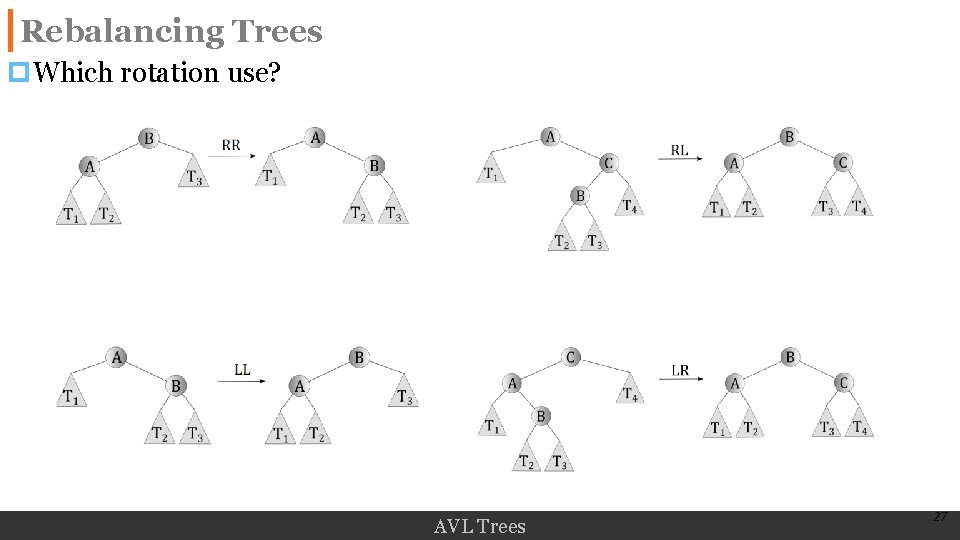
Rebalancing Trees p. Which rotation use? AVL Trees 27

『Case Study: The AVLTree Class』

AVLTree. java § This example gives the complete source code for the AVLTree class. § The AVLTree class extends the BST class (see Ch 08) to override the insert and delete methods to rebalance the tree if necessary. 29
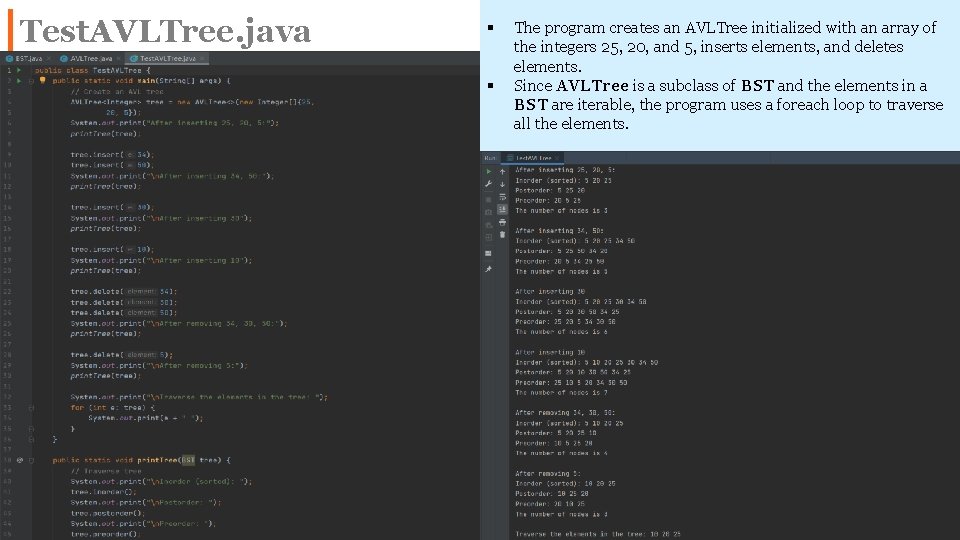
Test. AVLTree. java § § The program creates an AVLTree initialized with an array of the integers 25, 20, and 5, inserts elements, and deletes elements. Since AVLTree is a subclass of BST and the elements in a BST are iterable, the program uses a foreach loop to traverse all the elements. 30
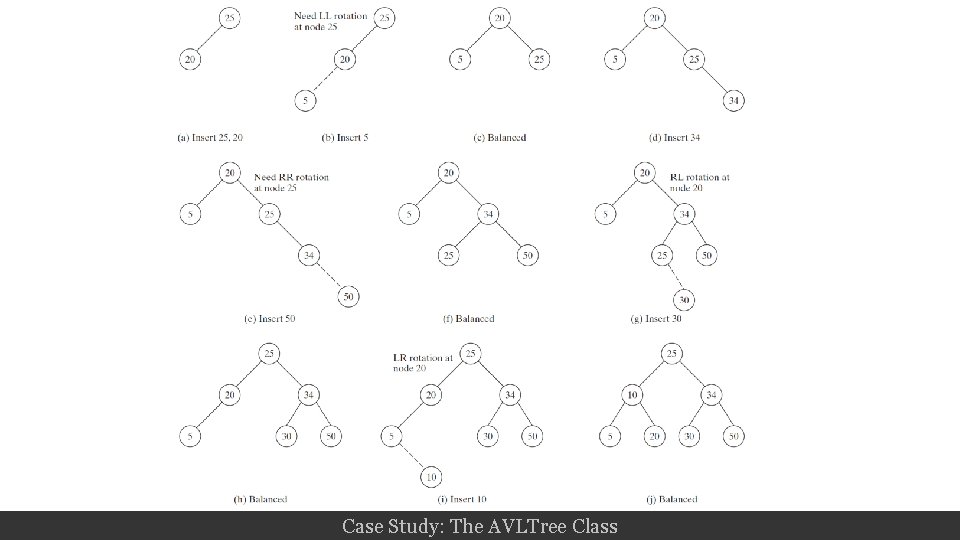
Case Study: The AVLTree Class

AVL Tree Time Complexity Analysis p. Since the height of an AVL tree is O(log n), the time complexity of the search, insert, and delete methods in AVLTree is O(log n). The time complexity of the search, insert, and delete methods in AVLTree depends on the height of the tree. We can prove that the height of the tree is O(log n). – Let G(h) denote the minimum number of nodes in an AVL tree with height h. Obviously, G(1) is 1 and G(2) is 2. The minimum number of nodes in an AVL tree with height h >= 3 must have two minimum subtrees: one with height h - 1 and the other with height h - 2. Thus, G(h) = G(h - 1) + G(h - 2) + 1 – Recall that a Fibonacci number at index i can be described using the recurrence relation F(i) = F(i - 1) + F(i - 2). Therefore, the function G(h) is essentially the same as F(i). It can be proven that h <1. 4405 log(n + 2) - 1. 3277 where n is the number of nodes in the tree. Hence, the height of an AVL tree is O(log n). – The search, insert, and delete methods involve only the nodes along a path in the tree. – The update. Height and balance. Factor methods are executed in a constant time for each node in the path. The balance. Path method is executed in a constant time for a node in the path. Thus, the time complexity for the search, insert, and delete methods is O(log n). AVL Trees 32
Agenda 提纲 01 Introduction 02 03 04 05 Rebalancing Trees The AVLTree class Chapter Summary Brainstorm

Chapter Summary p 1. An AVL tree is a well-balanced binary tree. In an AVL tree, the difference between the heights of two subtrees for every node is 0 or 1. p 2. The process for inserting or deleting an element in an AVL tree is the same as in a binary search tree. The difference is that you may have to rebalance the tree after an insertion or deletion operation. p 3. Imbalances in the tree caused by insertions and deletions are rebalanced through subtree rotations at the node of the imbalance. p 4. The process of rebalancing a node is called a rotation. There are four possible rotations: LL rotation, LR rotation, RR rotation, and RL rotation. p 5. The height of an AVL tree is O(log n). Therefore, the time complexities for the search, insert, and delete methods are O(log n). Summary 34
Agenda 提纲 01 Introduction 02 03 04 05 Rebalancing Trees The AVLTree class Chapter Summary Brainstorm

What’re the Pros and Cons of AVL Trees?

AVL Trees: Pros and Cons p AVL Trees 37
AVL Trees: Pros and Cons p. Further Reading – Pugh, W. Skip lists: a probabilistic alternative to balanced trees. Commun. ACM 33, 668– 676 (1990). AVL Trees 38

B tree

B tree p. The B tree was first described by Rudolf Bayer and Edward M. Mc. Creight in 1972. B Tree is a selfbalancing search tree. In most of the other self-balancing search trees (like AVL and Red-Black Trees), it is assumed that everything is in main memory. To understand the use of B-Trees, we must think of the huge amount of data that cannot fit in main memory. Rudolf Bayer (7 May 1939~) Germany 2001 ACM SIGMOD Edgar F. Codd Innovations Award Edward M. Mc. Creight Switzerland Rudolf Bayer and Mc. Creight, E. M. Organization and Maintenance of Large Ordered Indexes. Acta Informatica, 1, 173 -189, 1972. 40

Brainstorm Scientific Mindset 41

Brainstorm Further Information q The Java™ Tutorials. https: //docs. oracle. com/javase/tutorial/ q A brief history of java. https: //education. oracle. com/file/general/4955_Brief. History. Of. Java_7. pdf q Introduction to Java Programming and Data Structures, Comprehensive Version (11 th Edition). https: //media. pearsoncmg. com/ph/esm/ecs_liang_ijp_11/cw/content/source-code. php q Algorithms and Data Structures Animations. http: //www. cs. armstrong. edu/liang/animation. html q Check. Exercise. https: //liveexample-ppe. pearsoncmg. com/Check. Exercise/faces/Check. Exercise. xhtml q Data Structures and Algorithms in Java, 6 th Edition. http: //bcs. wiley. com/he-bcs/Books? action=chapter&bcs. Id=8634&item. Id=1118771338&chapter. Id=96645 q Data Structures and Algorithms in Python. https: //www. wiley. com/en-us/Data+Structures+and+Algorithms+in+Python-p-9781118290279 q Data Structures and Algorithm Analysis in C (2 nd Edition). https: //www. amazon. com/Data-Structures-Algorithm-Analysis-2 nd/dp/0201498405 q Source Code for Data Structures and Algorithm Analysis in C (Second Edition). https: //users. cs. fiu. edu/~weiss/dsaa_c 2 e/files. html q Mark Allen Weiss. https: //users. cs. fiu. edu/~weiss/ q Data Structures. http: //www. datastructures. info/ q Dictionary. http: //www. nist. gov/dads/ q Interactive Data Structure Visualizations. http: //www. student. seas. gwu. edu/~idsv/idsv. html q Java : Algorithms and Data Structure. https: //github. com/phishman 3579/java-algorithms-implementation q Algorithm Visualizer. https: //algorithm-visualizer. org/ q Visu. Algo - visualising data structures and algorithms. https: //visualgo. net/en 42

Confidential› 遇见更好的自己 The Power of Believing that You Can Improve. Dr. Zhiwen Hu @ http: //zhiwenhu. hustoj. com This presentation, slides, or hardcopy may NOT be used for short courses, industry seminars, or consulting purposes. The names of actual companies and products mentioned herein may be the trademarks of their respective owners. All rights reserved. Copyright © 2020. ›
- Slides: 43