PROFIL REGRESI I KORELASI I REGRESI DAN KORELASI

PROFIL REGRESI I KORELASI I REGRESI DAN KORELASI SEMESTER 2 REGRESI II KORELASI II PENUTUP

Profil kelompok 7 PROFIL REGRESI I KORELASI I Defita puteriyanti 11141477 Sherent haris syahputri 11141495 Muetia winda astuti 11141641 Dini nur indah diswari 11141682 Rahma aprilia handayani 11141704 REGRESI II Situs web kami: KORELASI II http: //statistikadeskriptifhlw 112 a 0507. wordpress. com/ PENUTUP NEXT

Tampilan web kelompok PROFIL REGRESI I KORELASI I REGRESI II KORELASI II PENUTUP BACK

Muetia winda astuti PROFIL REGRESI I NIM 11141641 KORELASI I Link web pribadi: https: //mutiawinda. wordpress. com/ REGRESI II KORELASI II PENUTUP NEXT

Tampilan web pribadi PROFIL REGRESI I KORELASI I REGRESI II KORELASI II PENUTUP BACK NEXT

Pengertian Regresi PROFIL REGRESI I KORELASI I REGRESI II KORELASI II q Regresi dan Korelasi digunakan untuk mempelajari dan mengukur hubungan statistik yang terjadi antara dua atau lebih. q Analisis regresi merupakan salah satu analisis yang bertujuan untuk mengetahui pengaruh suatu variabel terhadap variabel lain. q variabel yang mempengaruhi disebut variabel independent (variabel bebas) , biasanya dinyatakan dengan variabel X dan variabel yang dipengaruhi disebut dependent variabel (variabel terikat), biasanya dinyatakan dengan variabel Y. q jika dalam persamaan regresi hanya terdapat satu variabel terikat, maka disebut sebagai regresi sederhana. Sedangkan jika variabel bebasnya lebih dari satu, maka disebut sebagai persamaan regresi berganda. PENUTUP BACK NEXT

Rumus Regresi PROFIL REGRESI I y = a + bx rumus untuk meramalkan persamaan regresi maka nilai A dan B : KORELASI I REGRESI II KORELASI II PENUTUP BACK NEXT

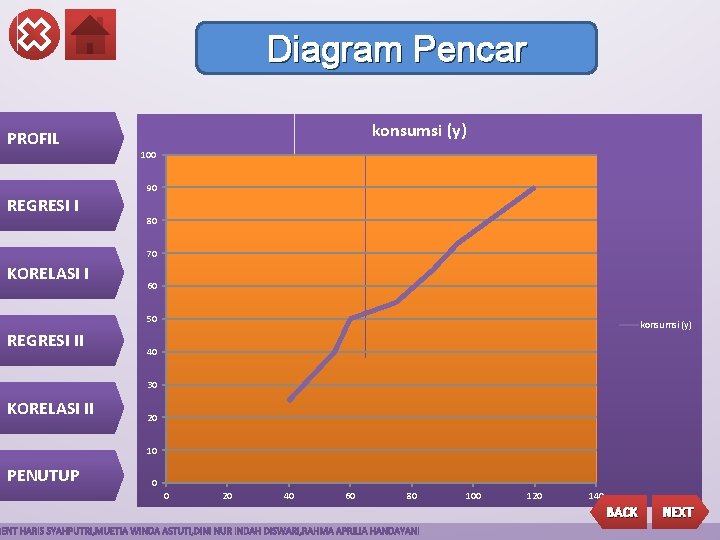
Contoh kasus PROFIL REGRESI I KORELASI I Apabila x= pendapatan (puluhan ribu rupiah) Y= konsumsi (puluhan ribu rupiah) x 40 55 60 75 87 95 120 y 25 40 50 55 65 73 90 REGRESI II KORELASI II PENUTUP a). Buatlah diagram pencarnya. b). Tentukan persamaan regresinya. c). Perkirakanlah besarnya pengeluaran untuk konsumsi jika pendapatannya Rp. 230. 000, 00 BACK NEXT

Diagram Pencar PROFIL konsumsi (y) 100 90 REGRESI I 80 70 KORELASI I 60 50 REGRESI II konsumsi (y) 40 30 KORELASI II 20 10 PENUTUP 0 0 20 40 60 80 100 120 140 BACK NEXT

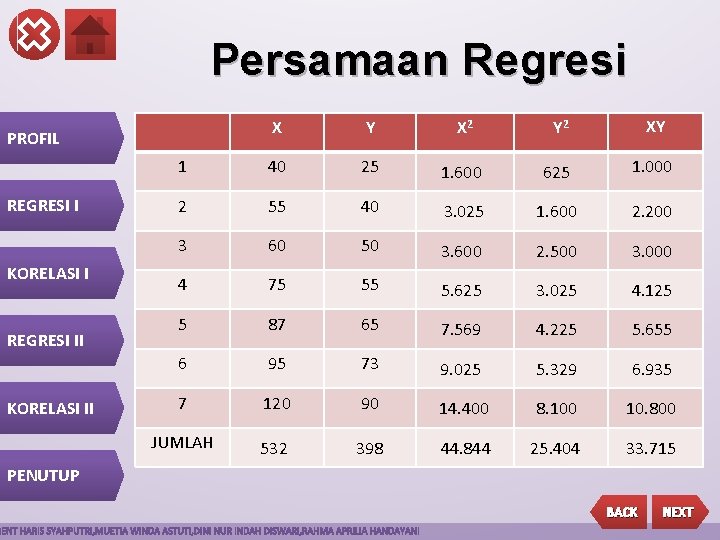
Persamaan Regresi X Y X 2 Y 2 XY 1 40 25 1. 600 625 1. 000 2 55 40 3. 025 1. 600 2. 200 3 60 50 3. 600 2. 500 3. 000 4 75 55 5. 625 3. 025 4. 125 5 87 65 7. 569 4. 225 5. 655 6 95 73 9. 025 5. 329 6. 935 7 120 90 14. 400 8. 100 10. 800 JUMLAH 532 398 44. 844 25. 404 33. 715 PROFIL REGRESI I KORELASI I REGRESI II KORELASI II PENUTUP BACK NEXT

Dari tabel di peroleh: N= 7 X=532 Y=398 X 2 =44. 845 Y 2 = 25. 404 XY= 33. 715 PROFIL REGRESI I KORELASI I REGRESI II KORELASI II PENUTUP BACK NEXT

Dari tabel di peroleh: N= 7 X=532 Y=398 X 2 =44. 845 Y 2 = 25. 404 XY= 33. 715 PROFIL REGRESI I KORELASI I REGRESI II KORELASI II PENUTUP BACK NEXT

PROFIL REGRESI I KORELASI I REGRESI II Y=-2, 864+0, 7858 x KORELASI II PENUTUP BACK NEXT

PROFIL REGRESI I KORELASI I REGRESI II KORELASI II § Perkirakanlah besarnya pengeluaran utk konsumsi jika pendapatannya Rp. 230. 000 : § Jika x=23 maka: Y= 2, 864+0, 7858(23) Y=2, 864+18, 0734 Y=20, 9374 PENUTUP BACK

Sherent haris syahputri PROFIL REGRESI I Nim 11141495 Link web pribadi: KORELASI I https: //sherenths. wordpress. com/ REGRESI II KORELASI II PENUTUP NEXT

Tampilan web prinadi PROFIL REGRESI I KORELASI I REGRESI II KORELASI II PENUTUP BACK NEXT

Korelasi PROFIL REGRESI I KORELASI I REGRESI II KORELASI II PENUTUP q. Analisa korelasi digunakan untuk mengukur kekuatan keeratan hubungan dua variabel melalui sebuah bilangan yang disebut KOEFISIEN KORELASI. q. Koefisien korelasi (r) adalah ukuran hubungan linier antara dua variabel x dan y untuk mengukur sejauh mana titik -titik menggerombol sekitar sebuah garis lurus regresi. BACK NEXT

Rumus Korelasi PROFIL REGRESI I KORELASI I REGRESI II KORELASI II PENUTUP BACK NEXT

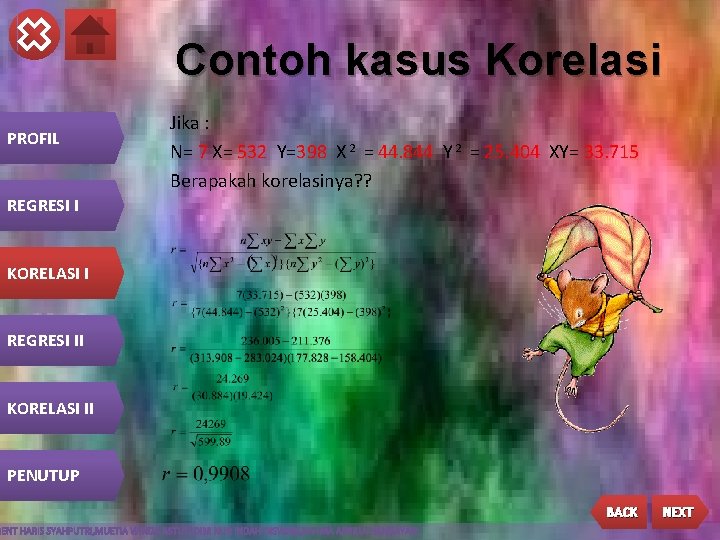
Contoh kasus Korelasi PROFIL Jika : N= 7 X= 532 Y=398 X 2 = 44. 844 Y 2 = 25. 404 XY= 33. 715 Berapakah korelasinya? ? REGRESI I KORELASI I REGRESI II KORELASI II PENUTUP BACK NEXT

Koefisien Determinasi PROFIL REGRESI I KORELASI I REGRESI II KORELASI II q. Koefisien determinasi adalah kuadrat dari koefisien korelasi q. Nilainya antara 0 dan 1 q. Untuk menyatakan proporsi keragaman total nilai-nilai peubah y yang dapat dijelaskan oleh nilai-nilai peubah x melalui hubungan linier tersebut. PENUTUP BACK NEXT

Contoh kasus Determinasi PROFIL REGRESI I Jika koefisien korelasi adalah 0, 9908 berapakah r 2 nya? ? ? KORELASI I REGRESI II KORELASI II PENUTUP BACK

Profil Pribadi PROFIL Dini Nur Indah Diswari 11141682 REGRESI I KORELASI I REGRESI II https: //dininurindah. wordpress. com/ KORELASI II PENUTUP BACK NEXT

Tampilan web pribadi PROFIL REGRESI I KORELASI I REGRESI II KORELASI II PENUTUP BACK NEXT

Definisi Regresi PROFIL REGRESI I KORELASI I REGRESI II Regresi adalah satu analisis yang bertujuan untuk mengetahui pengaruh suatu variabel terhadap varibel lain. . Dalam analisis regresi, variabel yang mempengaruhi disebut variabel independent variabel (variabel bebas) dan variabel yang dipengaruhi disebut dependent variabel (variabel terikat). jika dalam persamaan regresi hanya terdapat satu variabel terikat, maka disebut sebagai regresi sederhana. KORELASI II PENUTUP BACK NEXT

Untuk menentukan persamaan hubungan antar variabel, langkah-lakahnya sebagai berikut PROFIL 1. REGRESI I KORELASI I Mengumpulkan data dari variabel yang dibutuhkan misalnya X sebagai variabel bebas dan Y sebagai variabel tidak bebas. 2. Menggambarkan titik-titik pasangan (x, y) dalam sebuah sistem koordinat bidang. Hasil dari gambar itu disebut Scatter Diagram (Diagram Pencar/Tebaran) dimana dapat dibayangkan bentuk kurva halus yang sesuai dengan data. REGRESI II KORELASI II PENUTUP BACK NEXT

Rumus Regresi Sederhana PROFIL REGRESI I KORELASI I REGRESI II Y = a + b. X Keterangan : Y = variabel terikat (dependent variabel) X = variabel bebas (inpendent variabel) a = konstanta: dan b = koefisien regresi KORELASI II PENUTUP BACK NEXT

Dari Rumus Y = a + bx PROFIL REGRESI I KORELASI I REGRESI II KORELASI II PENUTUP BACK NEXT

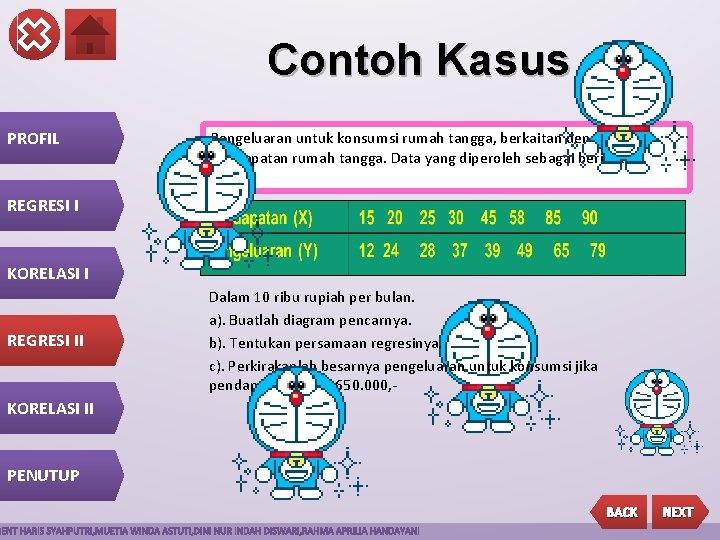
Contoh Kasus PROFIL Pengeluaran untuk konsumsi rumah tangga, berkaitan dengan pendapatan rumah tangga. Data yang diperoleh sebagai berikut: REGRESI I KORELASI I REGRESI II Dalam 10 ribu rupiah per bulan. a). Buatlah diagram pencarnya. b). Tentukan persamaan regresinya. c). Perkirakanlah besarnya pengeluaran untuk konsumsi jika pendapatannya Rp. 650. 000, - KORELASI II PENUTUP BACK NEXT

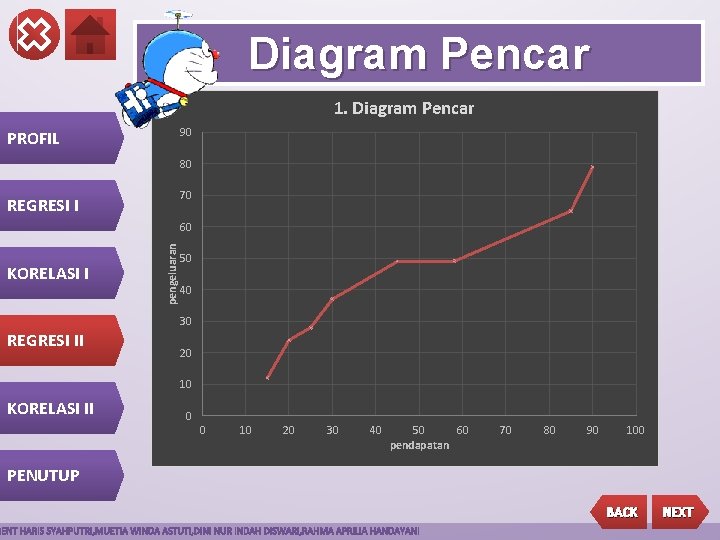
Diagram Pencar 1. Diagram Pencar 90 PROFIL 80 70 REGRESI I KORELASI I pengeluaran 60 50 40 30 REGRESI II 20 10 KORELASI II 0 0 10 20 30 40 50 60 pendapatan 70 80 90 100 PENUTUP BACK NEXT

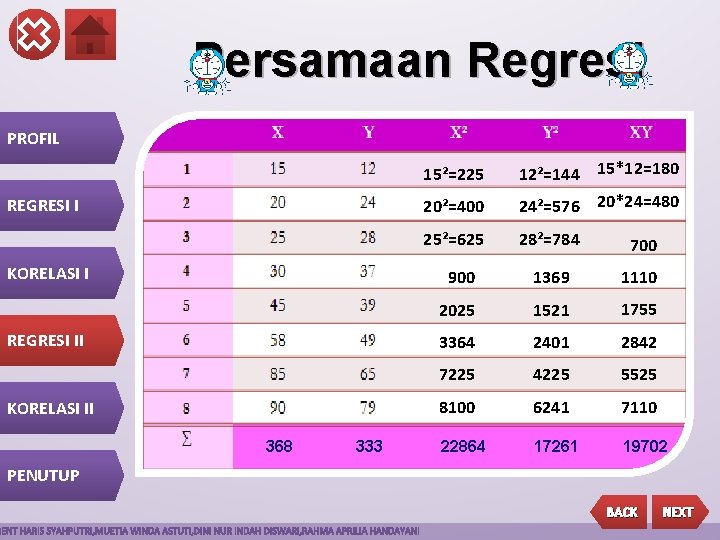
Persamaan Regresi PROFIL 20²=400 12²=144 15*12=180 24²=576 20*24=480 25²=625 28²=784 700 900 1369 1110 2025 1521 1755 3364 2401 2842 7225 4225 5525 8100 6241 7110 22864 17261 19702 15²=225 REGRESI I KORELASI I REGRESI II KORELASI II 368 333 PENUTUP BACK NEXT

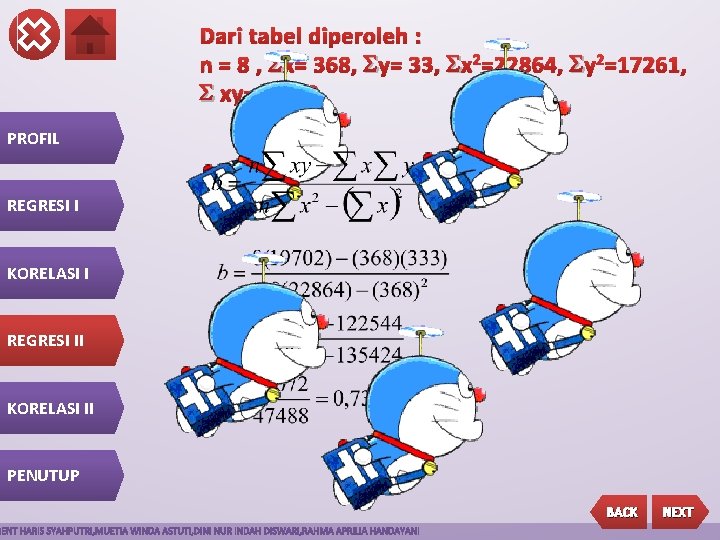
Dari tabel diperoleh : n = 8 , x= 368, y= 33, x 2 =22864, y 2 =17261, xy=19702 PROFIL REGRESI I KORELASI I REGRESI II KORELASI II PENUTUP BACK NEXT

Dari tabel diperoleh : n = 8 , x= 368, y= 33, x 2=22864, y 2=17261, xy=19702 PROFIL REGRESI I KORELASI I REGRESI II KORELASI II PENUTUP BACK NEXT

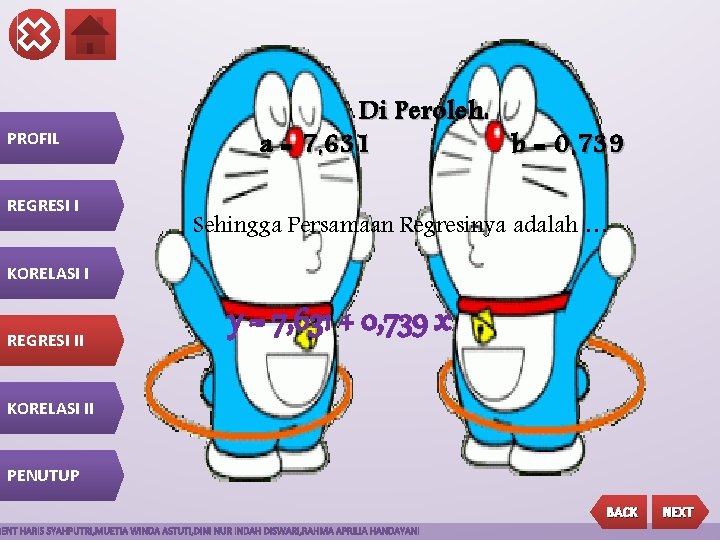
PROFIL REGRESI I Di Peroleh: a = 7, 631 b = 0, 739 Sehingga Persamaan Regresinya adalah … KORELASI I REGRESI II y = 7, 631 + 0, 739 x KORELASI II PENUTUP BACK NEXT

PROFIL REGRESI I KORELASI I REGRESI II Perkirakanlah besarnya pengeluaran untuk konsumsi jika pendapatannya Rp. 650. 000, Jika X = 65, maka: Y = 7, 631 + 0, 739 x Y = 7, 631 + 0, 739 (65) Y = 7, 631 + 48, 035 Y = 55, 666 KORELASI II PENUTUP BACK

Rahma Aprilia Handayani PROFIL REGRESI I KORELASI I Nim 11141704 Link web pribadi: https: //rahmaaprilia 271. wordpress. com/ REGRESI II KORELASI II PENUTUP NEXT

Tampilan Web Pribadi PROFIL REGRESI I KORELASI I REGRESI II KORELASI II PENUTUP BACK NEXT

Pengertian korelasi PROFIL REGRESI I KORELASI I REGRESI II Koefisien korelasi linier (r) adalah ukuran hubungan linier antara variabel/peubah acak X dan Y untuk mengukur sejauh mana titik-titik menggerombol sekitar sebuah garis lurus. KORELASI II PENUTUP BACK NEXT

Rumus Korelasi PROFIL REGRESI I KORELASI I REGRESI II KORELASI II PENUTUP BACK NEXT

Contoh kasus korelasi PROFIL Contoh : Pengeluaran untuk konsumsi rumah tangga berkaitan dengan pendapatan rumah tangga. Data yang diperoleh sebagai berikut : REGRESI I KORELASI I Pendapatan (X) 15 20 Pengeluaran (Y) 12 24 25 30 45 58 85 90 28 37 39 49 65 79 REGRESI II KORELASI II ØBuatlah koefisien korelasi ØBuatlah koefisien determinasi (r²) PENUTUP BACK NEXT

Contoh Kasus korelasi PROFIL REGRESI I KORELASI I REGRESI II KORELASI II PENUTUP Dari tabel diperoleh : n = 8, x= 368, y=333, x 2=22864, y 2=17261, xy=19702

Koefisien determinasi (r²) PROFIL REGRESI I KORELASI I untuk menyatakan proporsi keragaman total nilai peubah Y yang dapat dijelaskan oleh nilai peubah X melalui linier. REGRESI II KORELASI II PENUTUP BACK NEXT

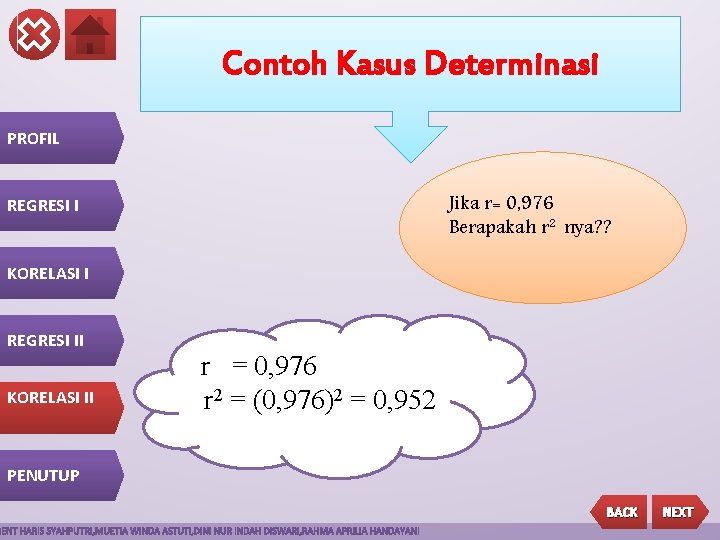
Contoh Kasus Determinasi PROFIL Jika r= 0, 976 Berapakah r 2 nya? ? REGRESI I KORELASI I REGRESI II KORELASI II r = 0, 976 r 2 = (0, 976)2 = 0, 952 PENUTUP BACK NEXT

PROFIL REGRESI I KORELASI I REGRESI II KORELASI II PENUTUP