Prof MSc Marcus Vinicius Santana https pt linkedin




























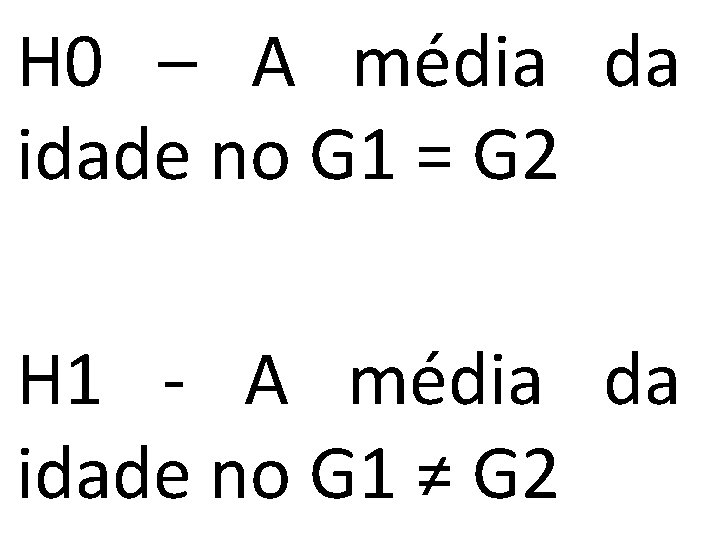
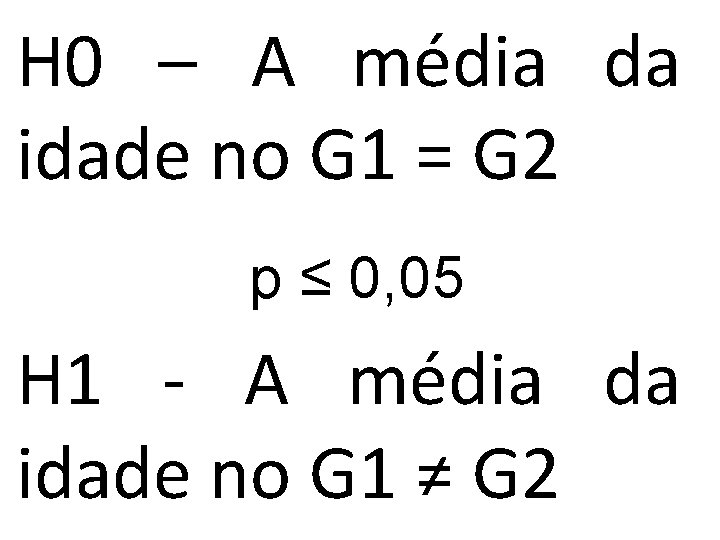

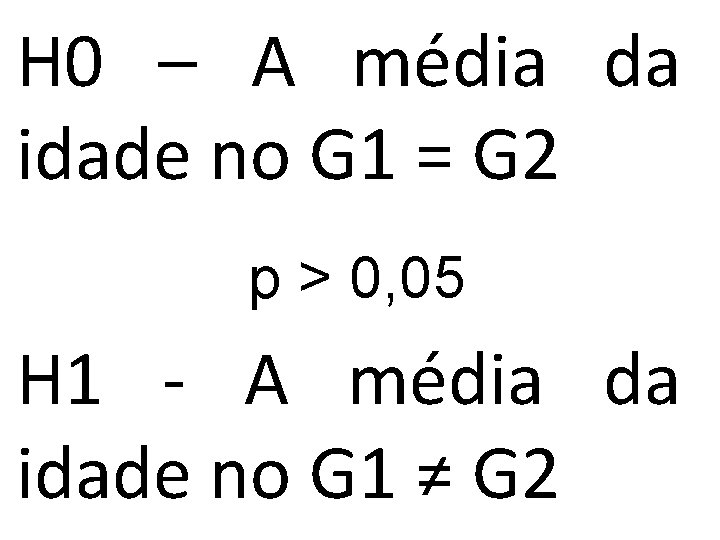



- Slides: 47

Prof. MSc Marcus Vinicius Santana

https: //pt. linkedin. com/pulse/como-mentir-com-estat%C 3%ADstica-um-guia-para-o-planejador-silveira http: //blog. opinionbox. com/mais-livros-essenciais-para-quem-faz-pesquisa-de-mercado/

https: //grazielase. wordpress. com/2014/01/17/geracao-barulho-nada-acrescenta-ao-pais-so-acrescenta-n-nas-estatisticas-deperturbacao-do-sossego-alheio/

http: //seguindopassoshistoria. blogspot. com. br/2012/03/falando-grego. html http: //tamararumoaoporto. blogspot. com. br/2014/07/rumo-grecia-aprendendo-grego. html Estatística

Variável • Quantitativa – Discreta – Contínua • Qualitativa – Nominal – Ordinal

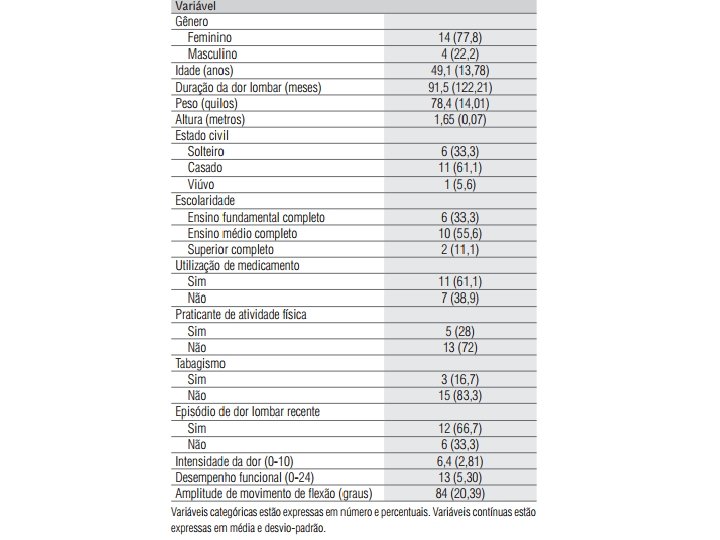
PARTICIPANTS INTERVENTION COMPARISONS OUTCOMES STUDY DESIGN

P A R T I C I P A N T S – Dor lombar crônica I N T E R V E N T I O N – Intervenções fisioterapêuticas C O M P A R I S O N S – Duas intervenções O U T C O M E S - Dor S TU DY D E S I G N – Ensaio clínico

• Estatística: é a ciência que coleta, sumariza, apresenta e interpreta informações (dados quantitativos), usando para isso, quando indicado, testes de hipóteses. http: //conre 3. org. br/novo_site/? q=content/banco-de-imagens

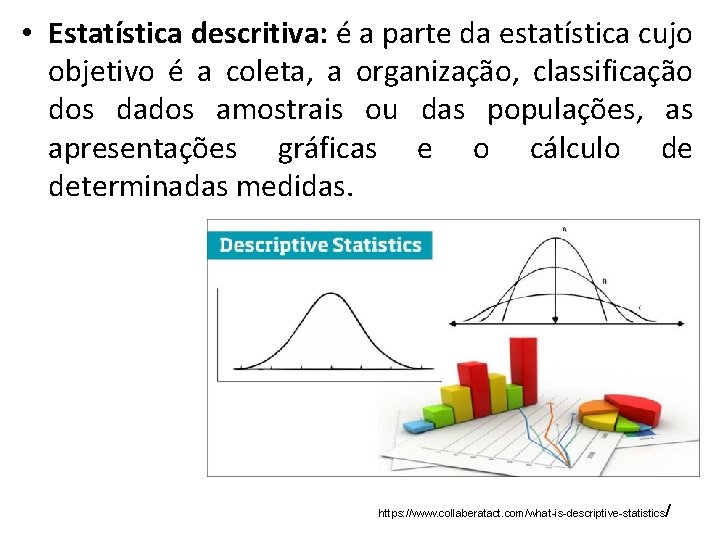
• Estatística descritiva: é a parte da estatística cujo objetivo é a coleta, a organização, classificação dos dados amostrais ou das populações, as apresentações gráficas e o cálculo de determinadas medidas. / https: //www. collaberatact. com/what-is-descriptive-statistics


Conceitos básicos • Medidas de tendência central • A maioria dos dados apresenta uma tendência de se concentrar em torno de um ponto central • Valor que descreve o conjunto – Média – Moda – Mediana

Média • Soma de todos os valores da observação dividido pelo número de observações envolvidas • Um ou mais valores discrepantes do conjunto podem distorcer a tendência apresentada pela média

Mediana • Expressa a posição central da distribuição quando a quantidade de números é ímpar • Números expressos em ordem crescente ou decrescente

Moda • Número ou números que mais se repetem

Um pouco de prática? http: //www. gazetadopovo. com. br/vida-publica/justica-e-direito/lei-de-arbitragem-aumenta-alcance-da-pratica-no-pais 8 nj 8 nmomnco 2 a 70 r 77 zt 7 czo 4

• A média ainda que considerada como um número que tem faculdade de representar uma série de valores não pode , por si mesma, destacar o grau de homogeinedade ou heterogeinedade que existe entre valores que compõem o conjunto

• Medida de dispersão É a maior ou menor diversificação dos valores de uma variável em torno de um valor de tendência central tomado como ponto de comparação

• Consideremos os seguintes conjuntos de valores das variáveis X, Y e Z: • X = { 70, 70, 70 } • Y = { 68, 69, 70 , 71 , 72 } • Z = { 5, 15, 50, 120, 160 } • Observamos então que os três conjuntos apresentam a mesma média aritmética = 350/5 = 70 • X é o grupo menos disperso

• Amplitude total • 40, 45, 48, 62 e 70 – At=70 – 40 = 30 • Amplitude interquartil • Terceiro – primeiro quartil • Desvio padrão • Mais utilizado porque envolve todos os valores

• Amplitude total • 40, 45, 48, 62 e 70 – At=70 – 40 = 30 • Amplitude interquartil • Terceiro – primeiro quartil • Desvio padrão • Mais utilizado porque envolve todos os valores

• Amplitude total • 40, 45, 48, 62 e 70 – At=70 – 40 = 30 • Amplitude interquartil • Terceiro – primeiro quartil • Desvio padrão http: //aprendendogestao. com. br/como-funciona-funcaoquartil-no-excel/ • Mais utilizado porque envolve todos os valores

• 40, 45, 48, 62 e 70 – At=70 – 40 = 30 • Amplitude interquartil • Terceiro – primeiro quartil • Desvio padrão • Mais utilizado porque envolve todos os valores http: //valeucara. blogspot. com. br/ 2016/10/media-desvio-e-erropadrao-no. html http: //brasilescola. uol. com. br/matematica/medidas-dispersao-variancia-desvio -padrao. htm • Amplitude total

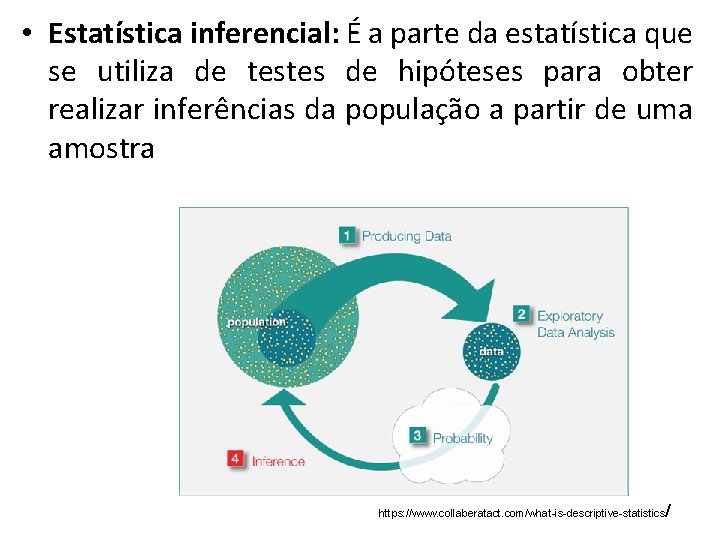
• Estatística inferencial: É a parte da estatística que se utiliza de testes de hipóteses para obter realizar inferências da população a partir de uma amostra / https: //www. collaberatact. com/what-is-descriptive-statistics

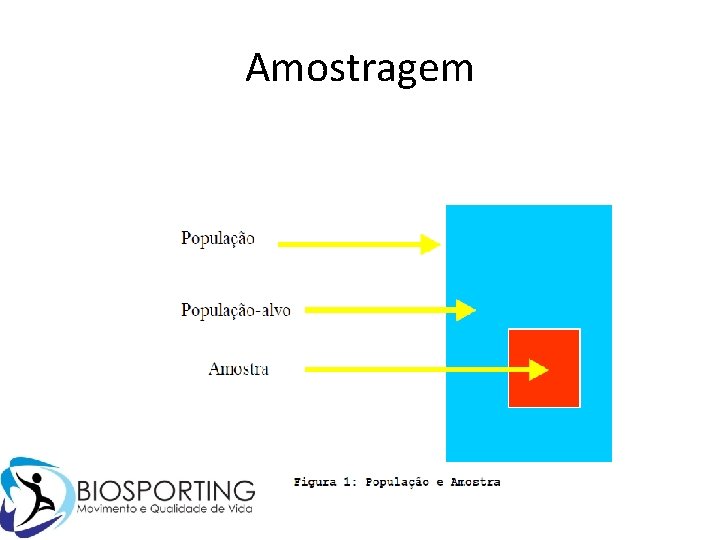
Amostragem

Exercício • Distribuição de dados – {2, 2, 3, 5} • • Média ? Desvio padrão Mediana Intervalo interquartil

Exercício • Distribuição de dados – {2, 2, 3, 5} • • Média ? – 2+2+3+5/4 = 3 Desvio padrão Mediana Intervalo interquartil

Exercício • Distribuição de dados – {2, 2, 3, 5} • • Média ? – 2+2+3+5/4 = 3 Desvio padrão (2 -3)²+(3 -3)²+(5 -2)² = ? Mediana Intervalo interquartil

Exercício • Distribuição de dados – {2, 2, 3, 5} • • Média ? – 2+2+3+5/4 = 3 Desvio (2 -3)²+(3 -3)²+(5 -2)² = 11 Mediana Intervalo interquartil

Exercício • Distribuição de dados – {2, 2, 3, 5} • • Média ? – 2+2+3+5/4 = 3 Desvio (2 -3)²+(3 -3)²+(5 -2)² = 11 Mediana Intervalo interquartil

Exercício • Distribuição de dados – {2, 2, 3, 5} • Média ? – 2+2+3+5/4 = 3 • Desvio padrão (2 -3)²+(3 -3)²+(5 -2)² = 11/4 -1 = 11/3 = 3. 66 SD =1. 91 • Mediana • Intervalo interquartil 3 ± 1. 91

Exercício • Distribuição de dados – {2, 2, 3, 5} • Média ? – 2+2+3+5/4 = 3 • Desvio padrão (2 -3)²+(3 -3)²+(5 -2)² = 11/4 -1 = 11/3 = 3. 66 • Mediana (2+3/2 = 2, 5) • Intervalo interquartil

Exercício • Distribuição de dados – {2, 2, 3, 5} • Média ? – 2+2+3+5/4 = 3 • Desvio padrão (2 -3)²+(3 -3)²+(5 -2)² = 11/4 -1 = 11/3 = 3. 66 • Mediana (2+3/2 = 2, 5) • Intervalo interquartil Q 1 = n+1/4 = 1, 25 = 2 • Q 3 = 3(n+1)/4 = 3, 75 = 4 2, 5 (4 -2)

Um pouco de prática? http: //www. gazetadopovo. com. br/vida-publica/justica-e-direito/lei-de-arbitragem-aumenta-alcance-da-pratica-no-pais 8 nj 8 nmomnco 2 a 70 r 77 zt 7 czo 4

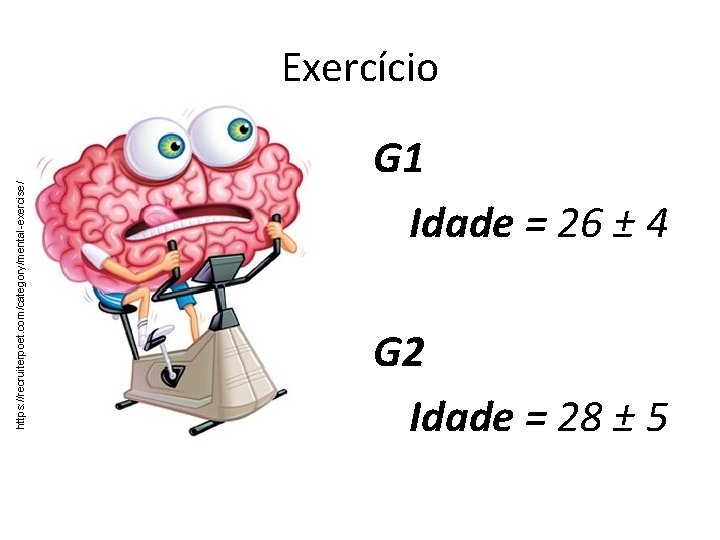
https: //recruiterpoet. com/category/mental-exercise/ Exercício G 1 Idade = 26 ± 4 G 2 Idade = 28 ± 5
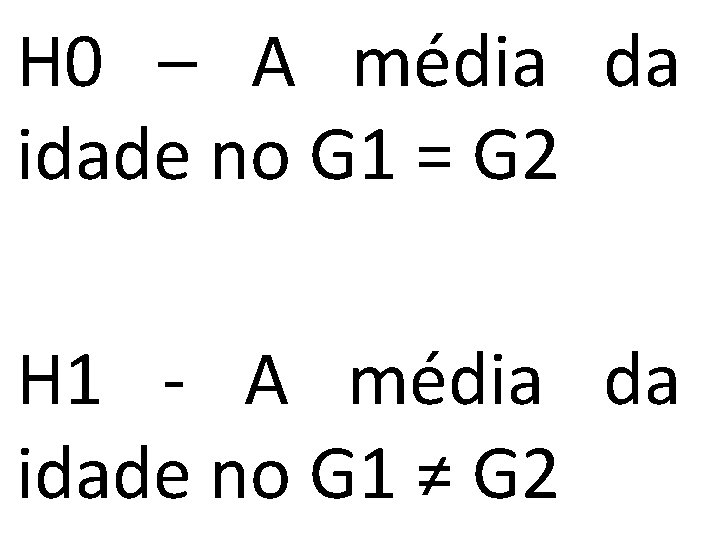
H 0 – A média da idade no G 1 = G 2 H 1 - A média da idade no G 1 ≠ G 2
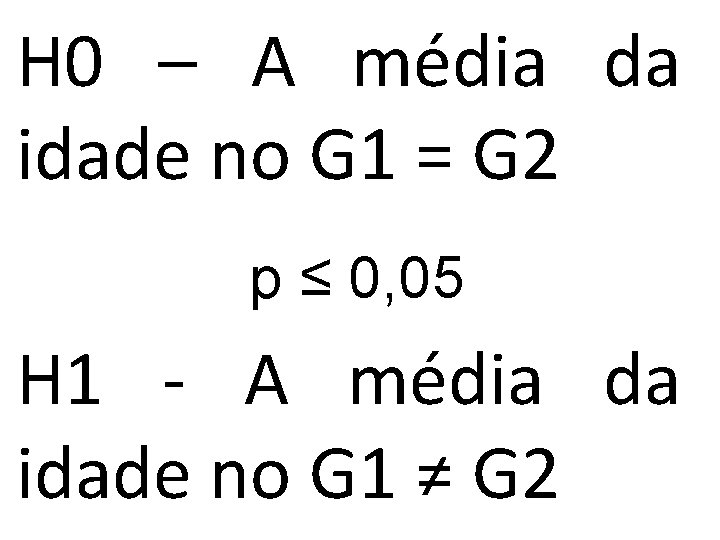
H 0 – A média da idade no G 1 = G 2 p ≤ 0, 05 H 1 - A média da idade no G 1 ≠ G 2

H 0 – A média da idade no G 1 = G 2 p ≤ 0, 05 H 1 - A média da idade no G 1 ≠ G 2
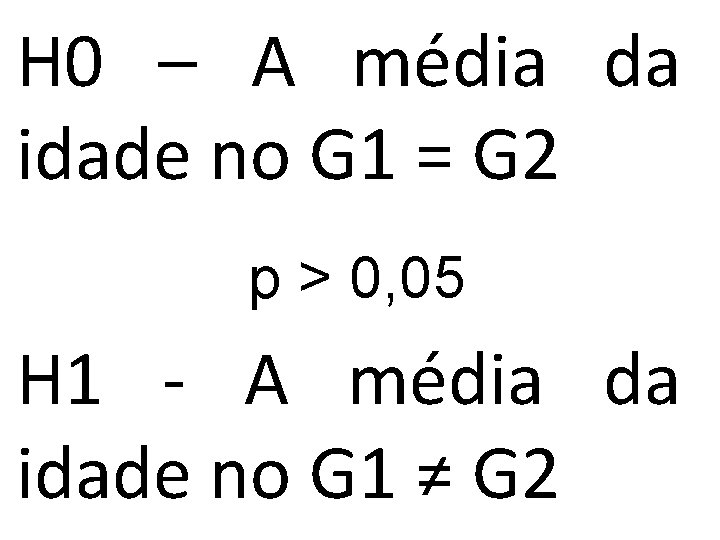
H 0 – A média da idade no G 1 = G 2 p > 0, 05 H 1 - A média da idade no G 1 ≠ G 2

H 0 – A média da idade no G 1 = G 2 p > 0, 05 H 1 - A média da idade no G 1 ≠ G 2

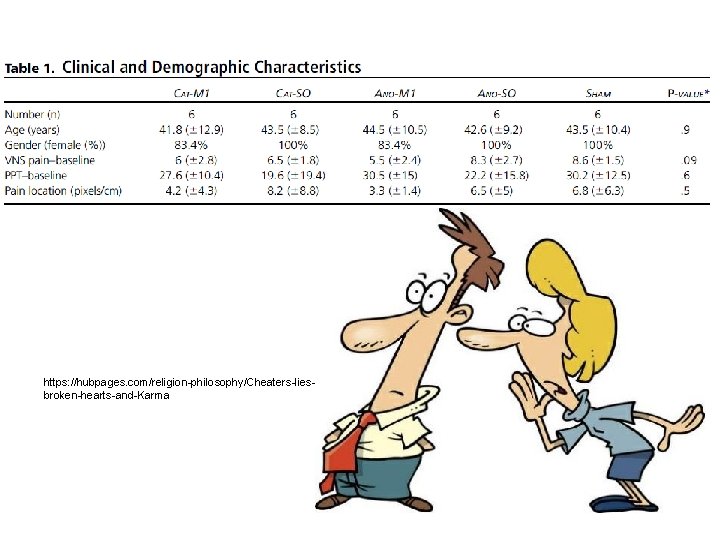
https: //hubpages. com/religion-philosophy/Cheaters-liesbroken-hearts-and-Karma


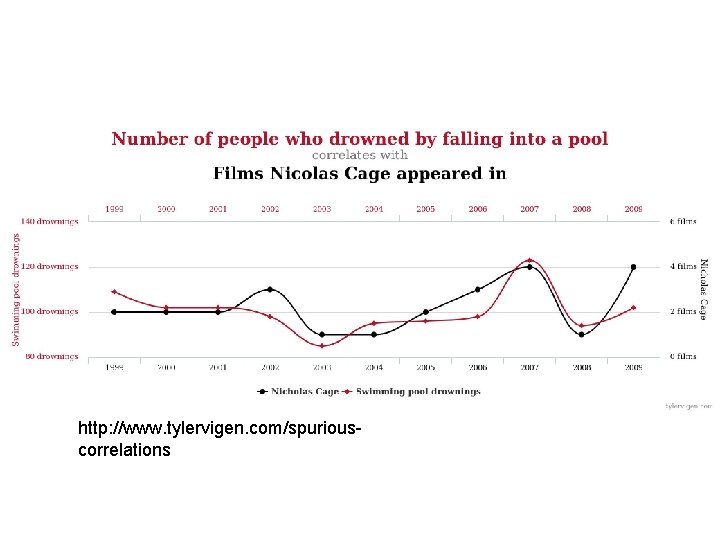
http: //www. tylervigen. com/spuriouscorrelations

http: //www. tylervigen. com/spuriouscorrelations

http: //www. tylervigen. com/spuriouscorrelations

http: //www. tylervigen. com/spuriouscorrelations


Insanidade é continuar fazendo sempre a mesma coisa e esperar resultados diferentes Albert Einstein