PRODUCT MOMENTS OF BIVARIATE RANDOM VARIABLES 8 1

PRODUCT MOMENTS OF BIVARIATE RANDOM VARIABLES 8. 1. Covariance of Bivariate Random Variables Definition 8. 1. Let X and Y be any two random variables with joint density function f(x, y). The product moment of X and Y , denoted by E(XY ), is defined as

Theorem 8. 1. Let X and Y be any two random variables. Then Cov(X, Y ) = E(XY ) − E(X)E(Y ). Proof: Cov(X, Y ) = E((X − μX) (Y − μY )) = E(XY − μX Y − μY X + μX μY ) = E(XY ) − μX E(Y ) − μY E(X) + μX μY = E(XY ) − μX μY − μY μX + μX μY = E(XY ) − E(X)E(Y ).

Example 8. 1. Let X and Y be discrete random variables with joint density What is the covariance "XY between X and Y. Answer: Cov(X, Y ) = E(XY ) − E(X)E(Y ) The marginal of X is

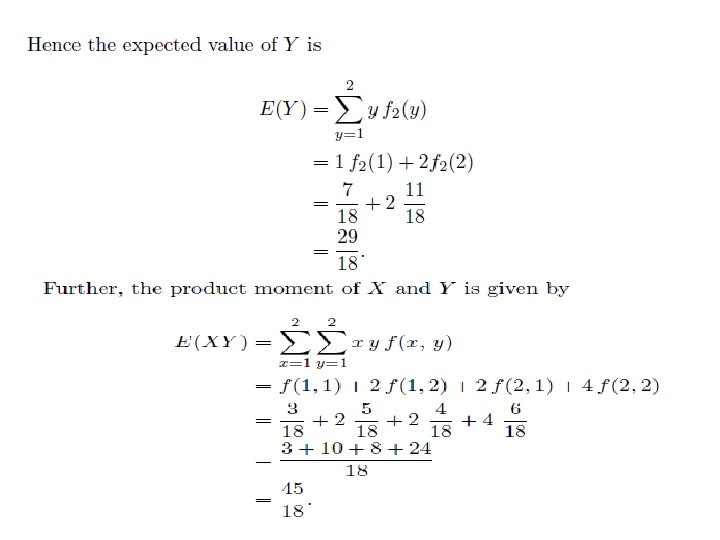
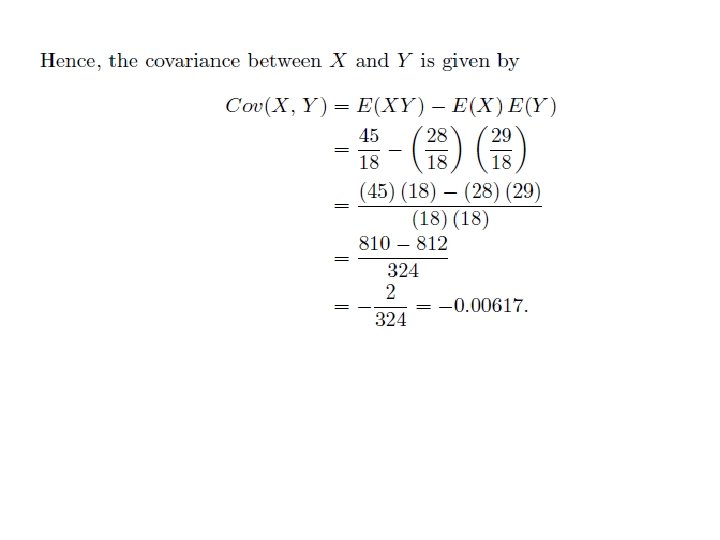

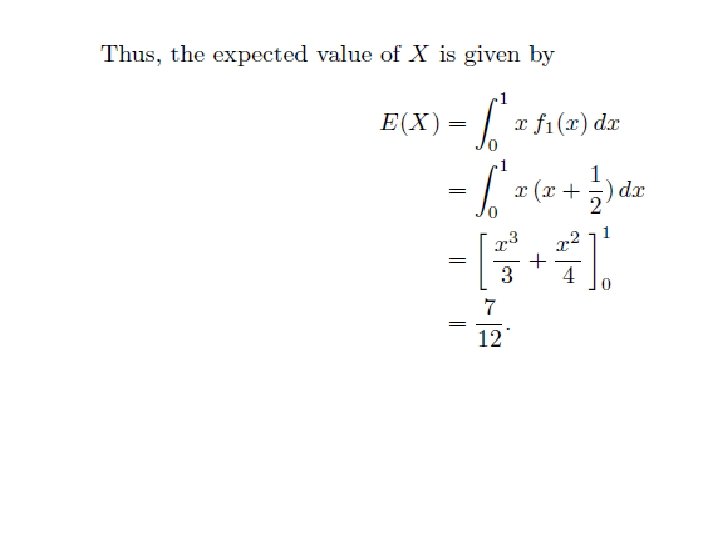


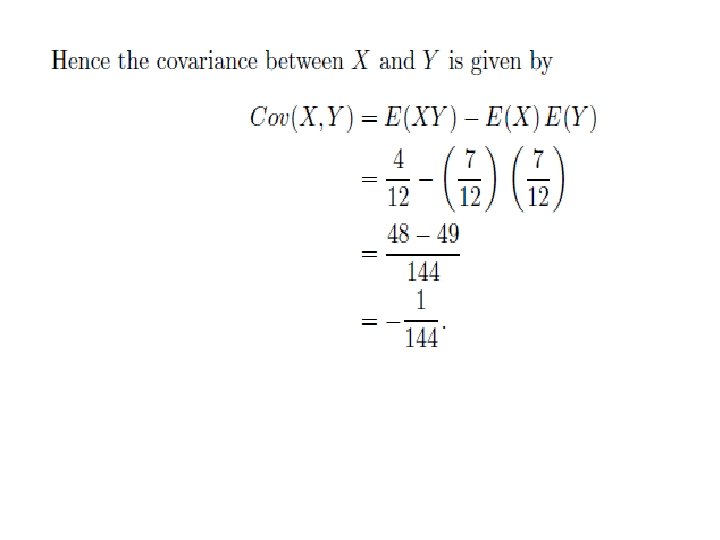

8. 2. Independence of Random Variables Theorem 8. 3. If X and Y are independent random variables, then E(XY ) = E(X)E(Y ). Theorem 8. 4. If X and Y are independent random variables, then the covariance between X and Y is always zero, that is Cov ( X, Y ) = 0.

Example 8. 6. Let the random variables X and Y have the joint density What is the covariance of X and Y ? Are the random variables X and Y independent?
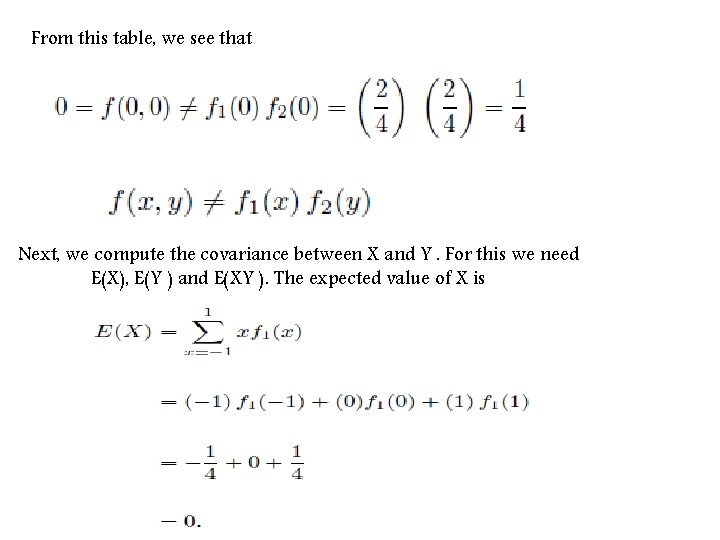
From this table, we see that Next, we compute the covariance between X and Y. For this we need E(X), E(Y ) and E(XY ). The expected value of X is

Hence, the covariance between X and Y is given by Cov(X, Y ) = E(XY ) − E(X)E(Y ) = 0

8. 4. Correlation and Independence Theorem 8. 7. If X and Y are independent, the correlation coefficient between X and Y is zero.

8. 5. Moment Generating Functions

What is the joint moment generating function for X and Y ? Answer: The joint moment generating function of X and Y is given by

Example 8. 11. If the joint moment generating function of the random variables X and Y is what is the covariance of X and Y ? Answer:

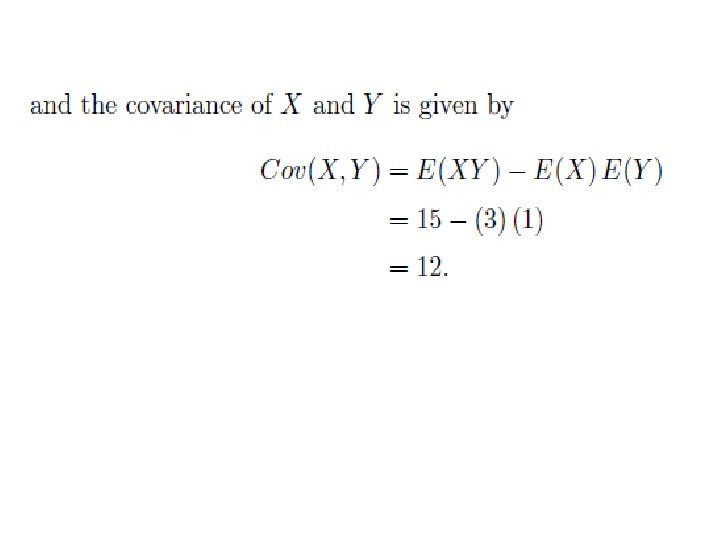
- Slides: 21