Product Moment Correlation Coefficient Use when you want

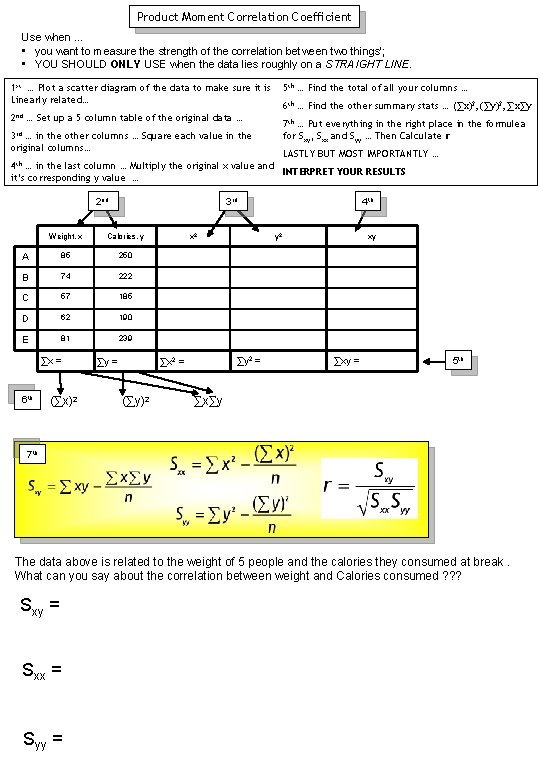
Product Moment Correlation Coefficient Use when … • you want to measure the strength of the correlation between two things’; • YOU SHOULD ONLY USE when the data lies roughly on a STRAIGHT LINE. 1 st … Plot a scatter diagram of the data to make sure it is Linearly related… 2 nd 5 th … Find the total of all your columns … 6 th … Find the other summary stats … (∑x)2, (∑y)2, ∑x∑y … Set up a 5 column table of the original data … 7 th … Put everything in the right place in the formulea for Sxy, Sxx and Syy … Then Calculate r 3 rd … in the other columns … Square each value in the original columns… LASTLY BUT MOST IMPORTANTLY … 4 th … in the last column … Multiply the original x value and INTERPRET YOUR RESULTS it’s corresponding y value … 2 nd 3 rd Weight, x Calories, y A 85 250 B 74 222 C 57 185 D 62 190 E 81 239 ∑x = 6 th (∑x)2 ∑y = x 2 (∑y)2 y 2 ∑y 2 = ∑x 2 = 4 th xy ∑xy = 5 th ∑x∑y 7 th The data above is related to the weight of 5 people and the calories they consumed at break. What can you say about the correlation between weight and Calories consumed ? ? ? Sxy = Sxx = Syy =

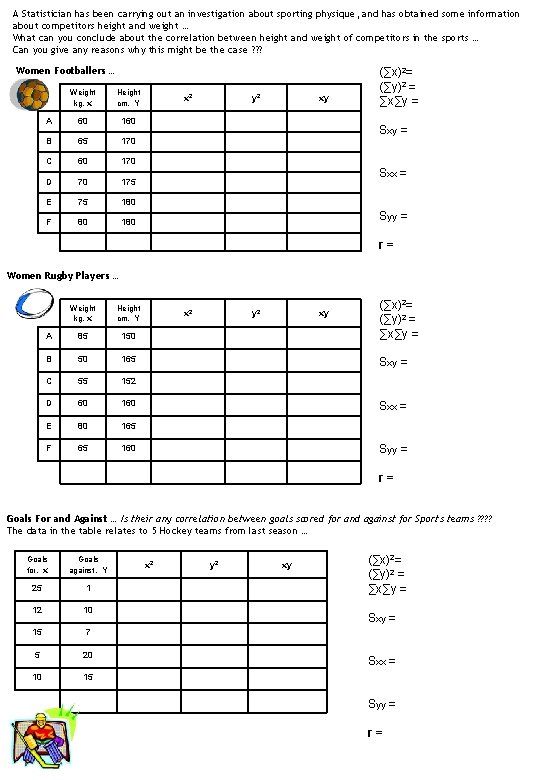
A Statistician has been carrying out an investigation about sporting physique, and has obtained some information about competitors height and weight … What can you conclude about the correlation between height and weight of competitors in the sports … Can you give any reasons why this might be the case ? ? ? Women Footballers … Weight kg, x Height cm, Y A 60 160 B 65 170 C 60 170 D 70 175 E 75 180 F 80 180 x 2 y 2 xy (∑x)2= (∑y)2 = ∑x∑y = Sxx = Syy = r= Women Rugby Players … Weight kg, x Height cm, Y A 85 150 B 50 165 C 55 152 D 60 160 E 80 165 F 65 160 x 2 y 2 xy (∑x)2= (∑y)2 = ∑x∑y = Sxx = Syy = r= Goals For and Against … Is their any correlation between goals scored for and against for Sports teams ? ? The data in the table relates to 5 Hockey teams from last season … Goals for, x Goals against, Y 25 1 12 10 15 7 5 20 10 15 x 2 y 2 xy (∑x)2= (∑y)2 = ∑x∑y = Sxx = Syy = r=