Processing and Analysis of Geometric Shapes Fast Marching

Processing and Analysis of Geometric Shapes Fast Marching Methods 1 Fast marching methods The continuous way © Alexander & Michael Bronstein, 2006 -2009 © Michael Bronstein, 2010 tosca. cs. technion. ac. il/book 048921 Advanced topics in vision Processing and Analysis of Geometric Shapes EE Technion, Spring 2010

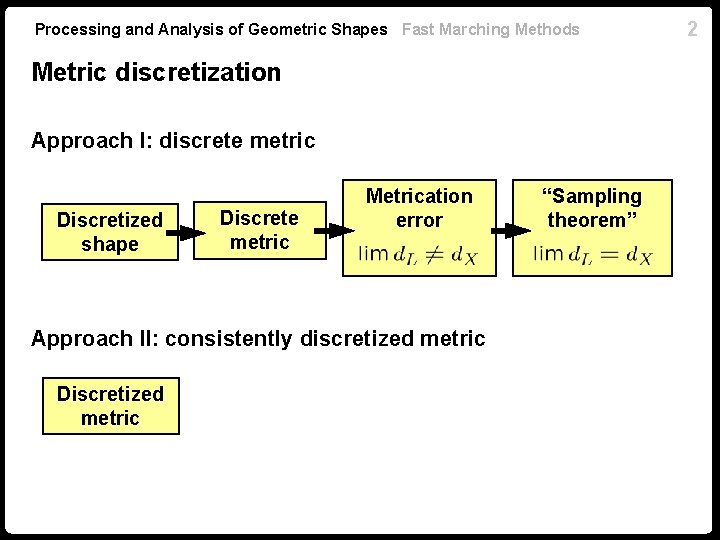
Processing and Analysis of Geometric Shapes Fast Marching Methods Metric discretization Approach I: discrete metric Discretized shape Discrete metric Metrication error Approach II: consistently discretized metric Discretized metric “Sampling theorem” 2

Processing and Analysis of Geometric Shapes Fast Marching Methods Fast marching algorithms 3

Processing and Analysis of Geometric Shapes Fast Marching Methods Forest fire n Fire starts at a source at . n Propagates with constant velocity n Arrives at time to a point n Fermat’s (least action) principle: The fire chooses the quickest path to travel. n Governs refraction laws in optics (Snell’s law) and acoustics. n Fire arrival time distance map = from source. . 4

Processing and Analysis of Geometric Shapes Fast Marching Methods Distance maps on surfaces n Distance map on surface n Mapped locally to the tangent space n A small step in the direction n changes the distance by is directional derivative in the direction . 5

Processing and Analysis of Geometric Shapes Fast Marching Methods Intrinsic gradient n For some direction , n The perpendicular direction is the direction of steepest change of the distance map. n is referred to as the intrinsic gradient. n Formally, the intrinsic gradient of function at a point is a map satisfying for any 6

Processing and Analysis of Geometric Shapes Fast Marching Methods Extrinsic gradient n Consider the distance map as a function n The extrinsic gradient of at a point . is a map satisfying for any direction n In the standard Euclidean basis n Usually called “the gradient” of . n What is the connection between intrinsic and extrinsic gradients? 7

Processing and Analysis of Geometric Shapes Fast Marching Methods Intrinsic and extrinsic gradients n Intrinsic gradient = projection of extrinsic gradient on tangent plane n In coordinates of a parametrization , n is the Jacobian matrix whose columns span . 8

9 Processing and Analysis of Geometric Shapes Fast Marching Methods Eikonal equation n Let be a minimal geodesic between and . n The derivative is the fire front propagation direction. n In arclength parametrization . n Fermat’s principle: n Propagation direction = direction of steepest increase of n Geodesic is perpendicular to the level sets of on . .

Processing and Analysis of Geometric Shapes Fast Marching Methods Eikonal equation n Eikonal equation (from Greek εικων) n Hyperbolic PDE with boundary condition n Minimal geodesics are characteristics. n Describes propagation of waves in medium. 10

Processing and Analysis of Geometric Shapes Fast Marching Methods Uniqueness of solution n In classic PDE theory, a solution is a continuous differentiable function satisfying n PDE theory guarantees existence and uniqueness of solution. n Distance map is not everywhere differentiable. n Solution is not unique! 1 D example 11

Processing and Analysis of Geometric Shapes Fast Marching Methods 12

Processing and Analysis of Geometric Shapes Fast Marching Methods Sub- and super-derivatives (1 D case) n Superderivative: the set of all slopes above the graph n Subderivative: the set of all slopes below the graph n where is differentiable. 13

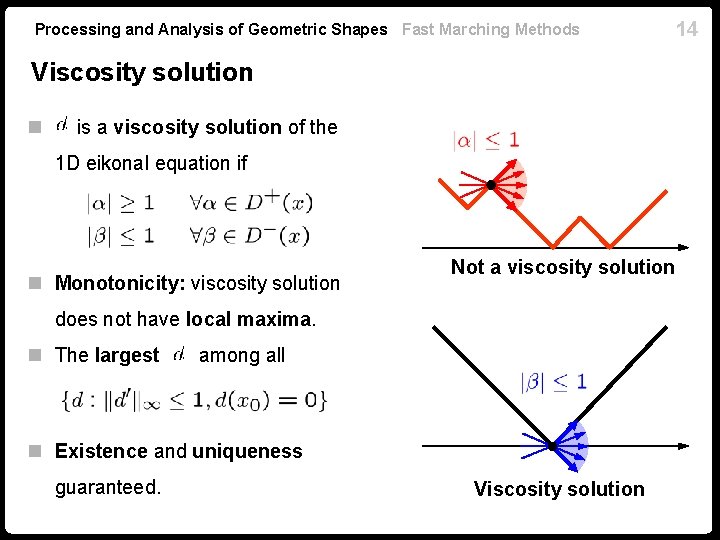
Processing and Analysis of Geometric Shapes Fast Marching Methods 14 Viscosity solution n is a viscosity solution of the 1 D eikonal equation if n Monotonicity: viscosity solution Not a viscosity solution does not have local maxima. n The largest among all n Existence and uniqueness guaranteed. Viscosity solution

Processing and Analysis of Geometric Shapes Fast Marching Methods Fast marching methods (FMM) n A family of numerical methods for solving eikonal equation. n Finds the viscosity solution = distance map. n Simulates wavefront propagation from a source set. n A continuous variant of Dijkstra’s algorithm. n Consistently approximate the intrinsic metric on the surface. 15

16 Processing and Analysis of Geometric Shapes Fast Marching Methods Dijkstra’s algorithm n Initialize and for the rest of the graph; Initialize queue of unprocessed vertices . n While n Find vertex with smallest value of , n For each unprocessed adjacent vertex n Remove from n Return distance map , . .

17 Processing and Analysis of Geometric Shapes Fast Marching Methods Fast marching algorithm n Initialize and mark it as black. n Initialize for other vertices and mark them as green. n Initialize queue of red vertices . n Repeat n Mark green neighbors of black vertices as red (add to ) n For each red vertex n For each triangle sharing the vertex Update n Mark from the triangle. with minimum value of as black (remove from n Until there are no more green vertices. n Return distance map . )

Processing and Analysis of Geometric Shapes Fast Marching Methods 18 Update step Dijkstra’s update n Vertex updated from adjacent vertex n Distance computed from n Path restricted to graph edges Fast marching update n Vertex n Distance from updated from triang computed and n Path can pass on mesh faces

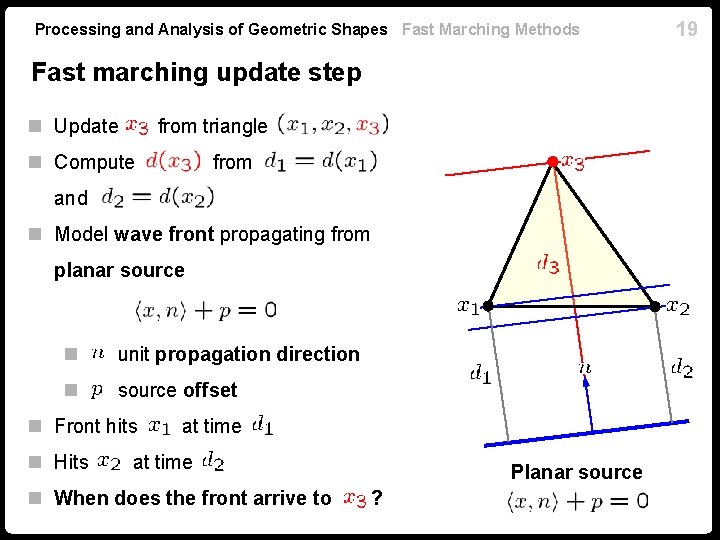
Processing and Analysis of Geometric Shapes Fast Marching Methods Fast marching update step n Update from triangle n Compute from and n Model wave front propagating from planar source n unit propagation direction n source offset n Front hits n Hits at time n When does the front arrive to Planar source ? 19

20 Processing and Analysis of Geometric Shapes Fast Marching Methods Fast marching update step n Assume w. l. o. g. n and . is given by the point-to-plane distance n Solve for parameters and using the point-to-plane distance n In vector notation where , n In a non-degenerate triangle matrix , and is full-rank .

Processing and Analysis of Geometric Shapes Fast Marching Methods Fast marching update step n Apparently, we have two equations with three variables. n However, is a unit vector, hence where . n Substitute . and obtain a quadratic equation 21

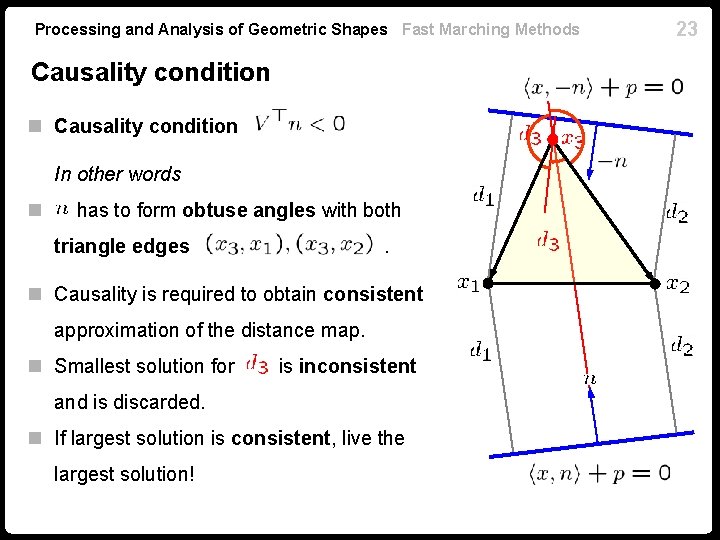
Processing and Analysis of Geometric Shapes Fast Marching Methods Causality condition n Quadratic equation is satisfied by both and . n Two solutions for n Causality: front can propagate only forward in time. n Causality condition 22

Processing and Analysis of Geometric Shapes Fast Marching Methods Causality condition n Causality condition In other words n has to form obtuse angles with both triangle edges . n Causality is required to obtain consistent approximation of the distance map. n Smallest solution for is inconsistent and is discarded. n If largest solution is consistent, live the largest solution! 23

Processing and Analysis of Geometric Shapes Fast Marching Methods Monotonicity condition n Viscosity solution has to be a monotonically increasing function. n Monotonicity condition: increase when In other words: n Differentiate w. r. t obtaining or increase. 24

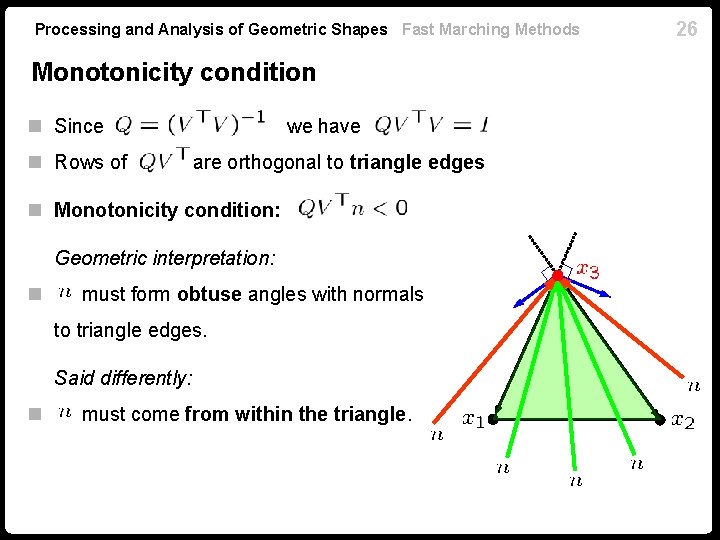
Processing and Analysis of Geometric Shapes Fast Marching Methods 25 Monotonicity condition n Substitute n Monotonicity satisfied when both coordinates of have the same sign. n is positive definite n Causality condition: n Monotonicity condition: At least one coordinate of is negative

Processing and Analysis of Geometric Shapes Fast Marching Methods Monotonicity condition n Since n Rows of we have are orthogonal to triangle edges n Monotonicity condition: Geometric interpretation: n must form obtuse angles with normals to triangle edges. Said differently: n must come from within the triangle. 26

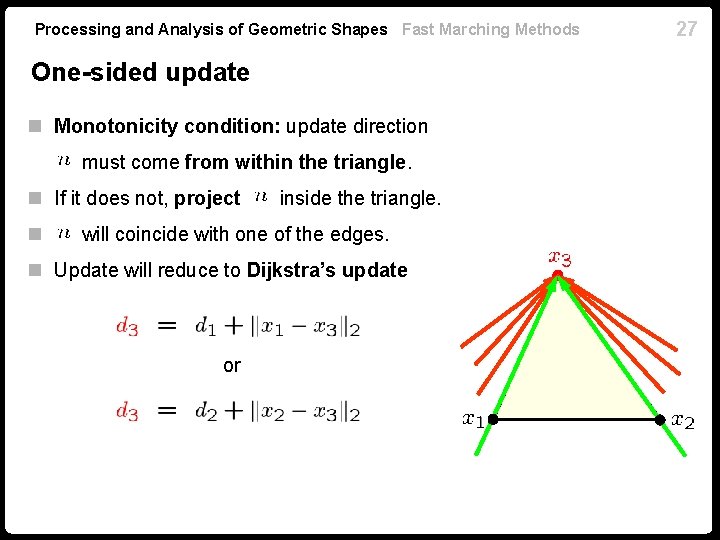
Processing and Analysis of Geometric Shapes Fast Marching Methods One-sided update n Monotonicity condition: update direction must come from within the triangle. n If it does not, project n inside the triangle. will coincide with one of the edges. n Update will reduce to Dijkstra’s update or 27

Processing and Analysis of Geometric Shapes Fast Marching Methods Fast marching update n Solve the quadratic equation and select the largest solution n Compute propagation direction n If monotonicity condition n Set is violated, 28

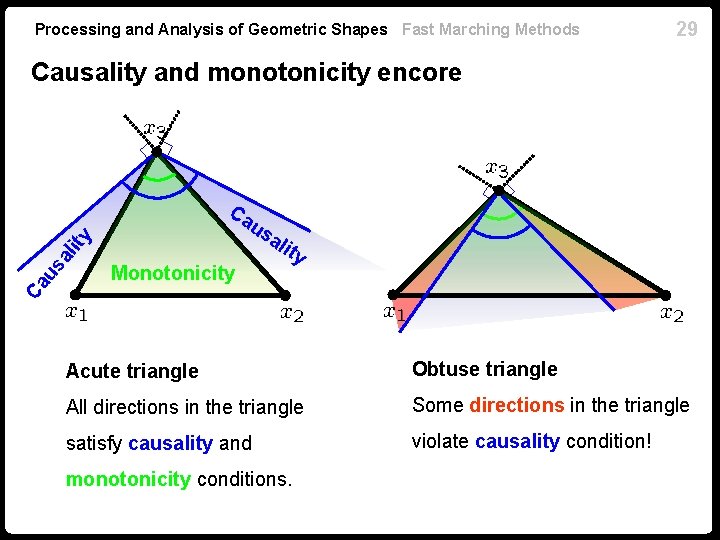
Processing and Analysis of Geometric Shapes Fast Marching Methods 29 Causality and monotonicity encore Ca us al ity Ca us Monotonicity ali ty Acute triangle Obtuse triangle All directions in the triangle Some directions in the triangle satisfy causality and violate causality condition! monotonicity conditions.

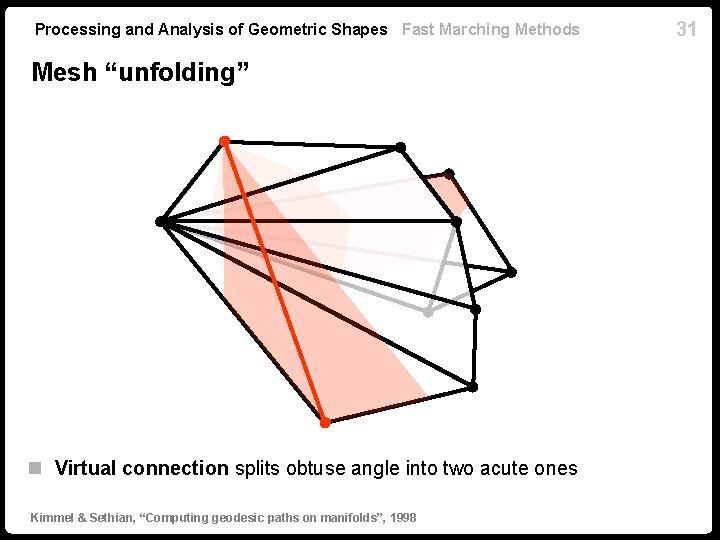
Processing and Analysis of Geometric Shapes Fast Marching Methods Fast marching on obtuse meshes n Inconsistent solution if the mesh contains obtuse triangles n Remeshing is costly n Solution: split obtuse triangles by adding virtual connections to non-adjacent vertices n Done as a pre-processing step in Kimmel & Sethian, “Computing geodesic paths on manifolds”, 1998 30

Processing and Analysis of Geometric Shapes Fast Marching Methods Mesh “unfolding” n Virtual connection splits obtuse angle into two acute ones Kimmel & Sethian, “Computing geodesic paths on manifolds”, 1998 31

Processing and Analysis of Geometric Shapes Fast Marching Methods ® MATLAB intermezzo Fast marching 32

Processing and Analysis of Geometric Shapes Fast Marching Methods 33

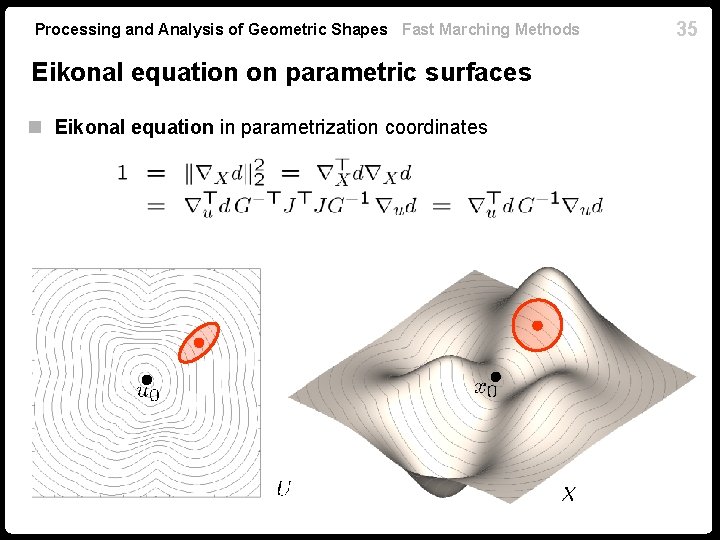
Processing and Analysis of Geometric Shapes Fast Marching Methods Eikonal equation on parametric surfaces n Parametrization of n Compute distance map from source over , . n Chain rule n Extrinsic gradient in parametrization coordinates n Intrinsic gradient in parametrization coordinates . 34

Processing and Analysis of Geometric Shapes Fast Marching Methods Eikonal equation on parametric surfaces n Eikonal equation in parametrization coordinates 35

Processing and Analysis of Geometric Shapes Fast Marching Methods Fast marching on parametric surfaces n Solve eikonal equation in parametrization domain n March on discretized parametrization domain. n We need to express update step in parametrization coordinates. 36

Processing and Analysis of Geometric Shapes Fast Marching Methods Fast marching on parametric surfaces n Cartesian sampling of with unit step. n Some connectivity (e. g. 4 - or 8 -neighbor). n Vertex updated from triangle n Assuming w. l. o. g. or in matrix form 37

Processing and Analysis of Geometric Shapes Fast Marching Methods Fast marching on parametric surfaces n Inner product matrix n Describes triangle geometry. n lengths of the edges. n n Substitute cosine of the angle. into the update quadratic equation n Only first fundamental form coefficients and grid connectivity are required for update. n Can measure distances when only surface gradients are known. 38

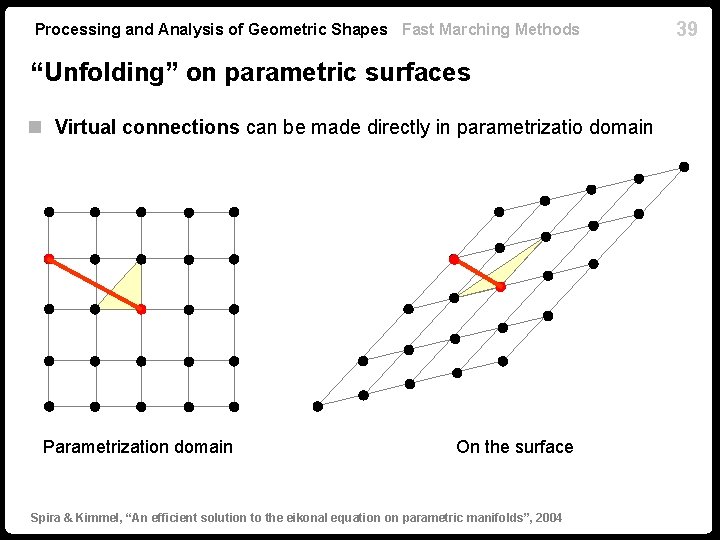
Processing and Analysis of Geometric Shapes Fast Marching Methods “Unfolding” on parametric surfaces n Virtual connections can be made directly in parametrizatio domain Parametrization domain On the surface Spira & Kimmel, “An efficient solution to the eikonal equation on parametric manifolds”, 2004 39

40 Processing and Analysis of Geometric Shapes Fast Marching Methods Heap-based grid update n Fast marching and Dijkstra’s algorithm use heap-based grid update. n Next vertex to be updated is decided by extracting the smallest . n Update order is unknown and data-dependent. n Inefficient use of memory system and cache. n Inherently sequential algorithm – next update depends on previous one. n Can we do better? n Regular access to memory (known in advance). n Vectorizable (parallelizable) algorithm.

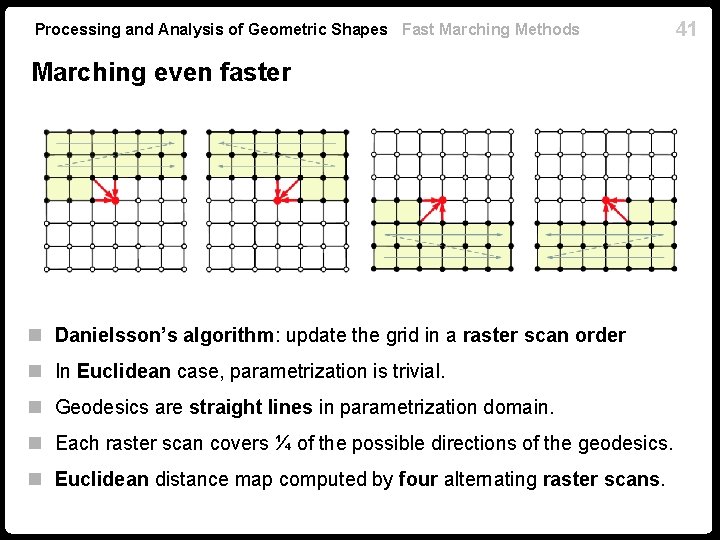
Processing and Analysis of Geometric Shapes Fast Marching Methods Marching even faster n Danielsson’s algorithm: update the grid in a raster scan order n In Euclidean case, parametrization is trivial. n Geodesics are straight lines in parametrization domain. n Each raster scan covers ¼ of the possible directions of the geodesics. n Euclidean distance map computed by four alternating raster scans. 41

42 Processing and Analysis of Geometric Shapes Fast Marching Methods Raster scan fast marching n Generally, geodesics are curved in parametrization domain. n Raster scans have to be repeated to 1 iteration 4 iterations 2 iterations 5 iterations 3 iterations 6 iterations produce a convergent solution. n Iterative algorithm. n Number of iterations depends on geometry and parametrization. n Practically, few iterations are required.

Processing and Analysis of Geometric Shapes Fast Marching Methods ® MATLAB intermezzo Raster scan fast marching 43

Processing and Analysis of Geometric Shapes Fast Marching Methods Raster scan fast marching n What we lost: n No more a one-pass algorithm. n Computational complexity is data-dependent. n What we found: n Coherent memory access, efficient use of cache. n No heap, each iteration is . n Raster scans can be parallelized. BBK, "Parallel algorithms for approximation of distance maps on parametric surfaces”, 2007 44

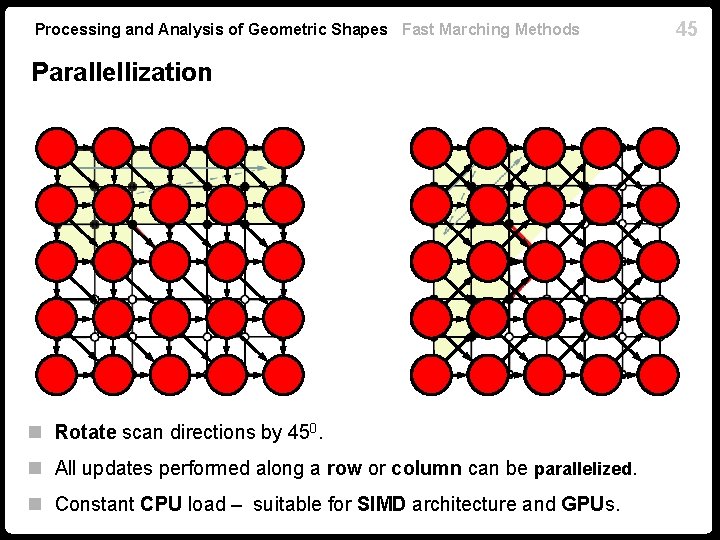
Processing and Analysis of Geometric Shapes Fast Marching Methods Parallellization n Rotate scan directions by 450. n All updates performed along a row or column can be parallelized. n Constant CPU load – suitable for SIMD architecture and GPUs. 45

Processing and Analysis of Geometric Shapes Fast Marching Methods Parallel marching n Rotate scan directions by 450. n All updates performed along a row or column can be parallelized. n Constant CPU load. n Suitable for SIMD architecture and GPUs. n GPU implementation computes geodesic on grid with 10, 000 vertices in less than 50 msec. n About 200 million distances per second! 46

Processing and Analysis of Geometric Shapes Fast Marching Methods Minimal geodesics n We have a numerical tool to compute geodesic distance. n Sometimes, the shortest path itself is needed. n Minimal geodesics are characteristics of the eikonal equation. In other words: n Along geodesic, eikonal equation becomes an ODE with initial condition n Solve the ODE for . . 47

Processing and Analysis of Geometric Shapes Fast Marching Methods 48 Minimal geodesics n To find a minimal geodesic between two points n Compute distance map from n Starting at to all other points. , follow the direction of n Steepest descent on the distance map. In the parametrization coordinates n Let be the preimage of in until is reached.

Processing and Analysis of Geometric Shapes Fast Marching Methods Minimal geodesics n Substitute into characteristic equation n Steepest descent on surface = scaled steepest descent in parametrization domain. 49

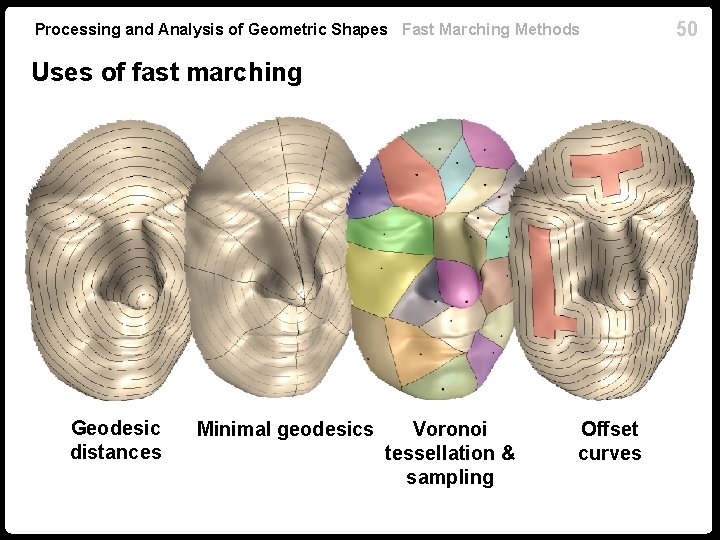
Processing and Analysis of Geometric Shapes Fast Marching Methods Uses of fast marching Geodesic distances Minimal geodesics Voronoi tessellation & sampling Offset curves 50

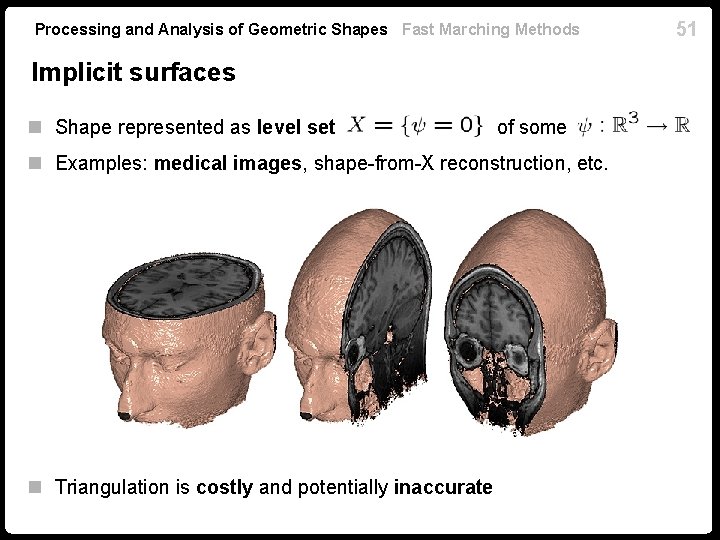
Processing and Analysis of Geometric Shapes Fast Marching Methods Implicit surfaces n Shape represented as level set of some n Examples: medical images, shape-from-X reconstruction, etc. n Triangulation is costly and potentially inaccurate 51

Processing and Analysis of Geometric Shapes Fast Marching Methods Implicit surfaces n Two-manifold n Narrow band of radius n Co-dimension 1 n Three-manifold with boundary n smooth if 52

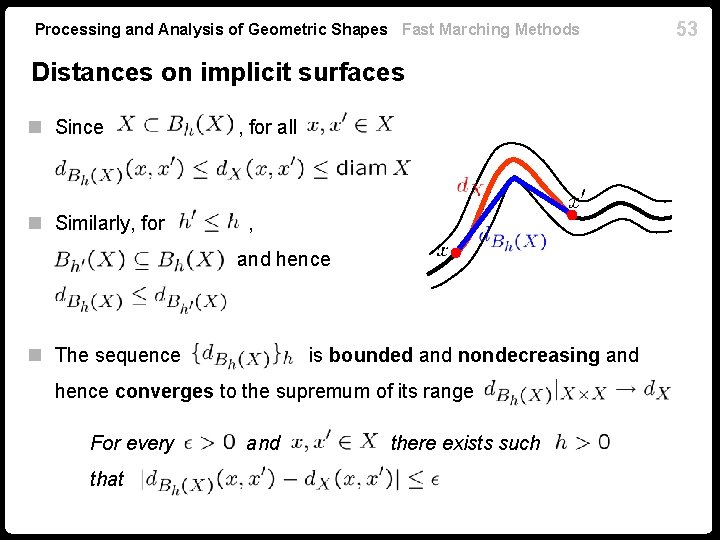
Processing and Analysis of Geometric Shapes Fast Marching Methods Distances on implicit surfaces n Since n Similarly, for all , and hence n The sequence is bounded and nondecreasing and hence converges to the supremum of its range For every that and there exists such 53

Processing and Analysis of Geometric Shapes Fast Marching Methods 54 Distances on implicit surfaces n Uniform convergence of geodesic distances: For every there exists an such that for every , n If then where is a constant dependent on the geometry of n Convergence of minimal geodesics: Let be a unique minimal geodesic between and let geodesic on be a minimal. Then Memoli & Sapiro, “Fast computation of weighted distance functions and geodesics on implicit hyper-surfaces”, 2001

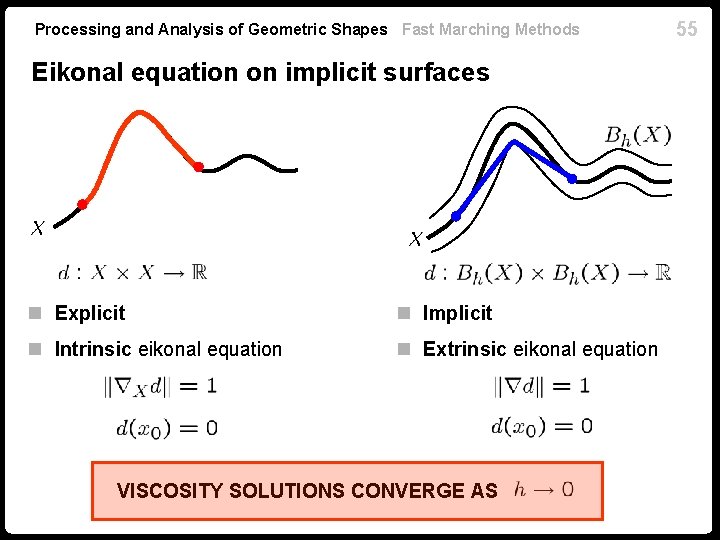
Processing and Analysis of Geometric Shapes Fast Marching Methods Eikonal equation on implicit surfaces n Explicit n Implicit n Intrinsic eikonal equation n Extrinsic eikonal equation VISCOSITY SOLUTIONS CONVERGE AS 55

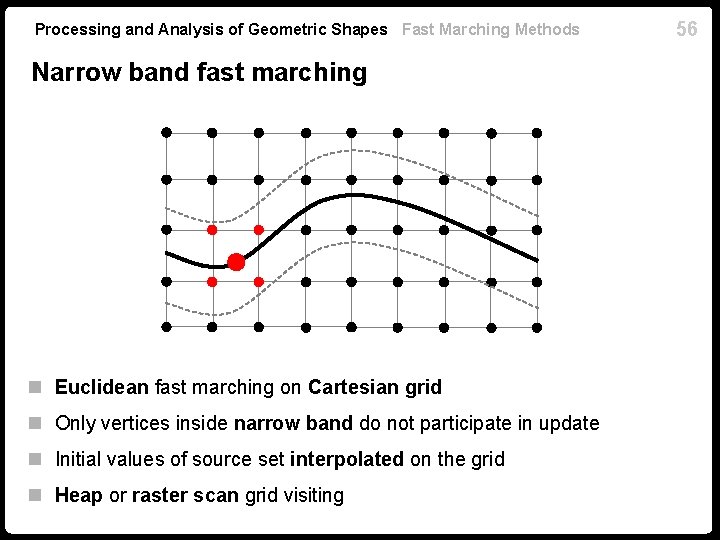
Processing and Analysis of Geometric Shapes Fast Marching Methods Narrow band fast marching n Euclidean fast marching on Cartesian grid n Only vertices inside narrow band do not participate in update n Initial values of source set interpolated on the grid n Heap or raster scan grid visiting 56