PROCESS UNDERSTANDING The Foundation of process control is

PROCESS UNDERSTANDING The Foundation of process control is “ Process Understanding”

System Representation 1. System Representation (Mathematically) (Differential Equations of a system) (Transfer function of A system) (Modeling of some Analogous Systems) (Mechanical-Electrical) (State Space Equations) 2. System Representation (Graphically) (Block Diagram & Block Diagram Reduction) (Signal Flow Graph)

System Representation 1. System Representation (Mathematically) Differential Equations (DEs) Models derived from basic physical laws that describe the process. - Ohm’s law, Kirchoff’s law - Newton’s law Transfer Function (TF) State Space Equations (SS) TF=Laplace Transform(system output)/Laplace Transform (system input) under assumption all initial conditions equal zero. SS transforms n th order differential equation into n set of first order differential equations. System Analysis requires transformation of DEs into TF. It introduces state variable/s that could be used to define any entity within the system that sometimes is not possible to measure but affects the system.

System Representation Mathematically-Differential Equations (Modeling of some Analogous Systems) (Translational Mechanical-Electrical)

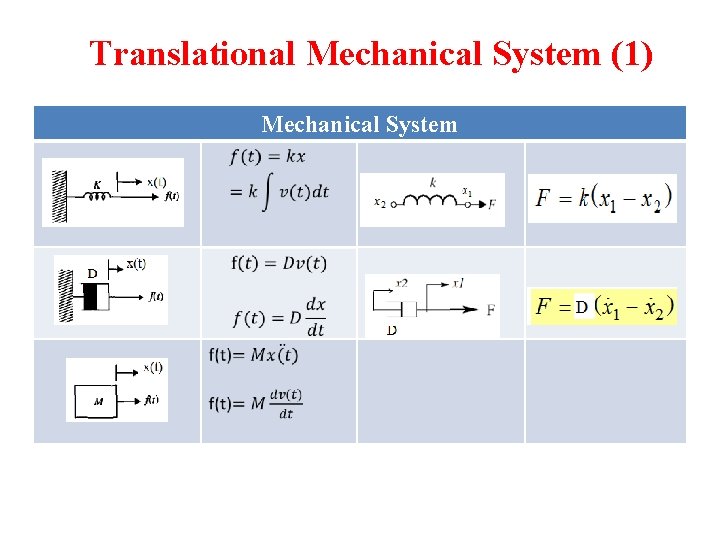
Translational Mechanical System (1) Mechanical System

Translational Mechanical System (2) • The general procedure for mechanical systems is as follows i. iii. iv. v. vii. Adopt a suitable co-ordinate system with an appropriate sign convention. For linear motion, up is positive and left to right is positive. Identify any disturbing forces acting on the system (inputs to the system). Identify displacements and/or velocities (outputs from the system). Draw a free body diagram for each mass showing all the forces and moments acting on it. Apply Newton's 2 nd Law to each free body diagram (F = Mass x Acceleration). Rearrange the equation(s) into a suitable form for solution by a convenient method. Note that unless otherwise specified, ignore gravitational effects.

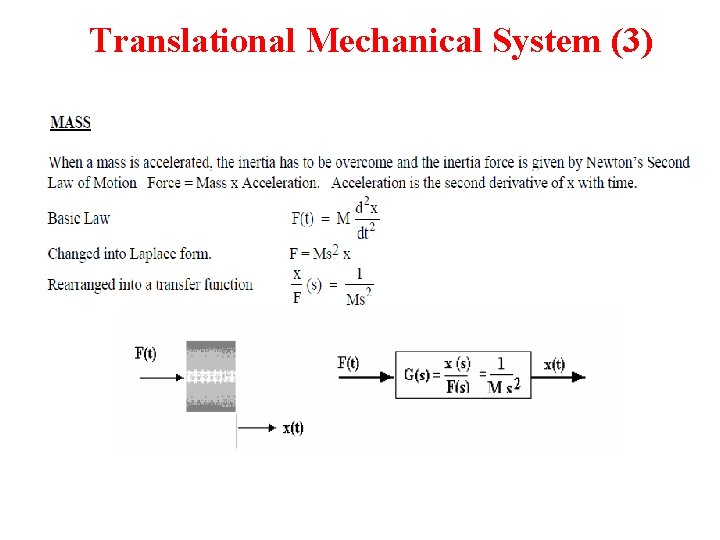
Translational Mechanical System (3)

Translational Mechanical System (4)

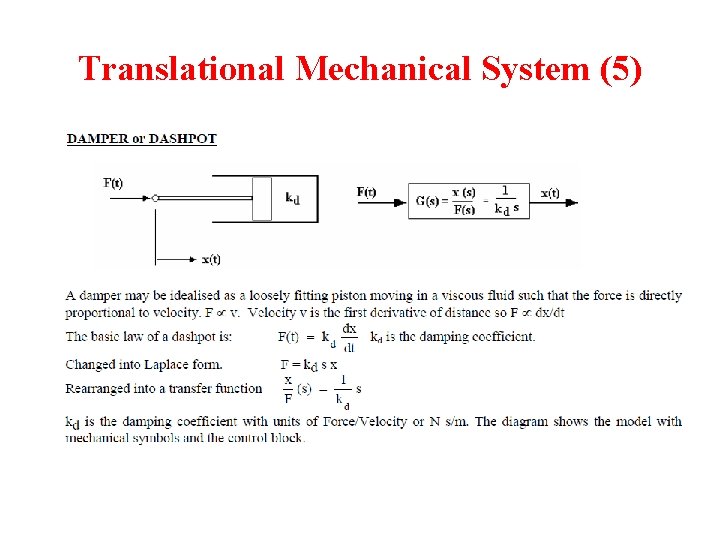
Translational Mechanical System (5)

Translational Mechanical System (6)

Translational Mechanical System (7)

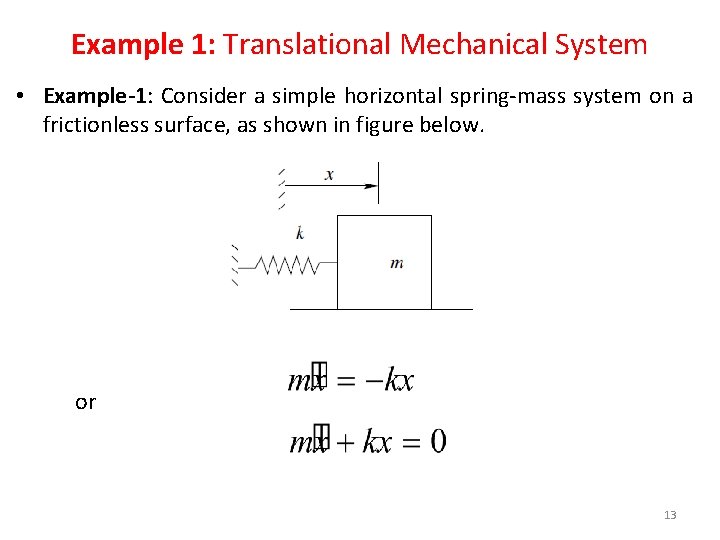
Example 1: Translational Mechanical System • Example-1: Consider a simple horizontal spring-mass system on a frictionless surface, as shown in figure below. or 13

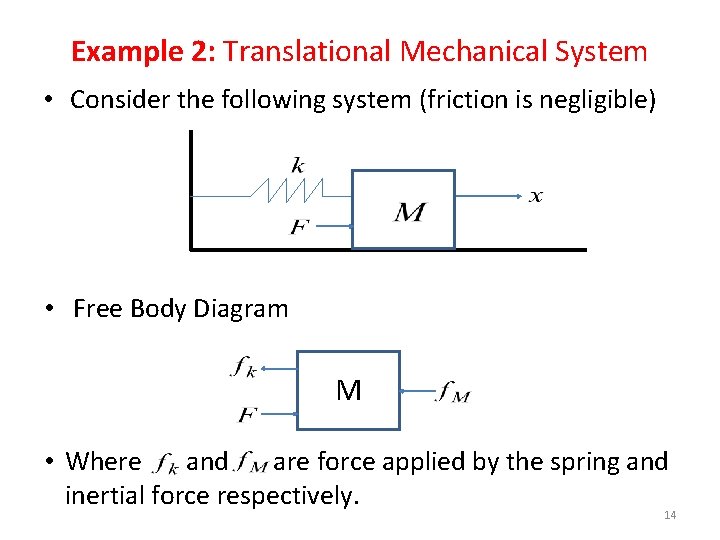
Example 2: Translational Mechanical System • Consider the following system (friction is negligible) • Free Body Diagram M • Where and are force applied by the spring and inertial force respectively. 14

Example 2: Translational Mechanical System M • Then the differential equation of the system is: • Taking the Laplace Transform of both sides and ignoring initial conditions we get 15

Example 2: Translational Mechanical System • The transfer function of the system is • if 16

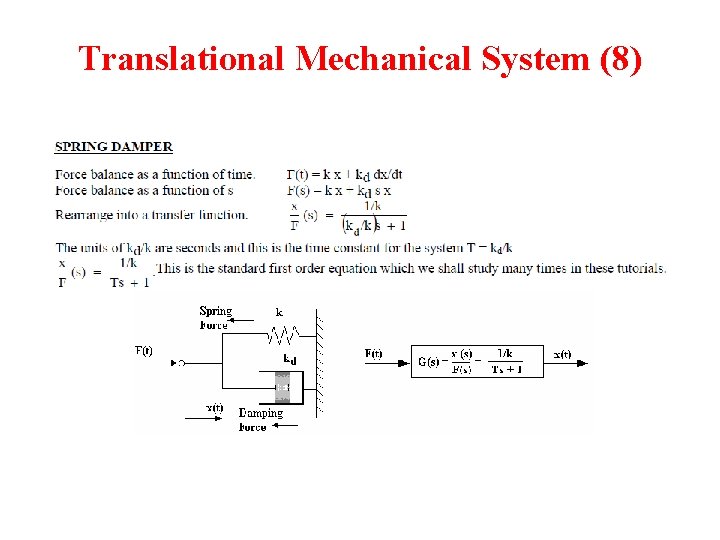
Translational Mechanical System (8)

Translational Mechanical System (9)

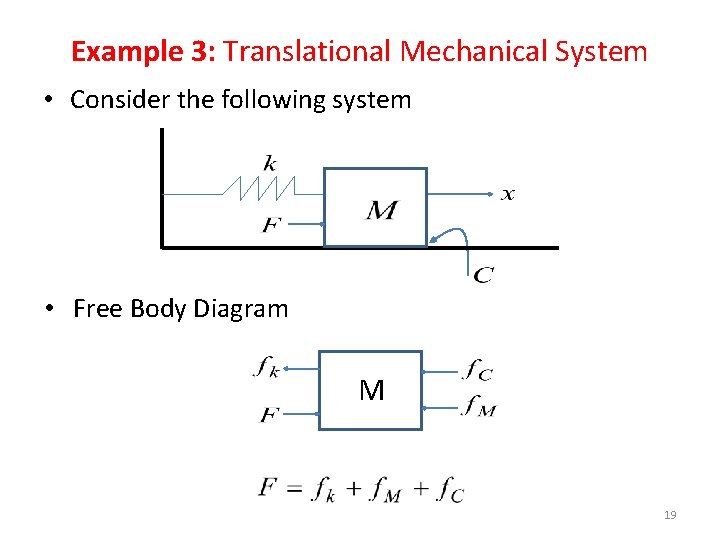
Example 3: Translational Mechanical System • Consider the following system • Free Body Diagram M 19

Example 3: Translational Mechanical System Differential equation of the system is: Taking the Laplace Transform of both sides and ignoring Initial conditions we get 20

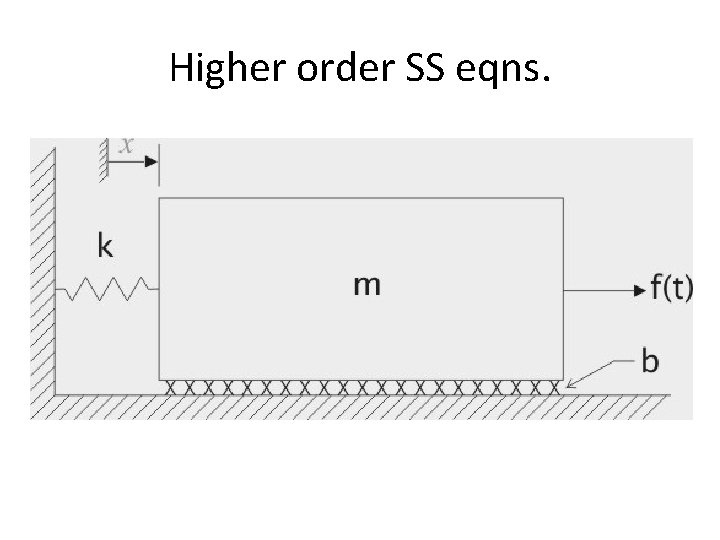
Higher order SS eqns.

• f(t) - kx - bx' - mx" = 0 • Taking the Laplace Transform of the governing equation results in: • F(s) - k[X(s)] - b[s. X(s)] - m[s 2 X(s)] = 0 • Collecting all the terms involving X(s) and factoring leads to: • [ms 2 + bs + k] X(s) = F(s) 22

Transfer Function • The transfer function is defined as the output Laplace Transform over the input Laplace Transform, and so the transfer function of this second order system is: • X(s)/F(s) = 1/[ms 2 + bs + k] • COMMAND: transferfunction = tf(num, den) 23

• Input X(s)/F(s) = 1/[ms 2 + bs + k] into MATLAB: • Let m = 2, b = 5, and k = 3. • >> m = 2; >> b = 5; >> k = 3; >> num = [ 1 ]; >> den = [ m b k ]; >> tutorial_tf = tf(num, den) • Transfer function: 1 -------2 s^2 + 5 s + 3 24

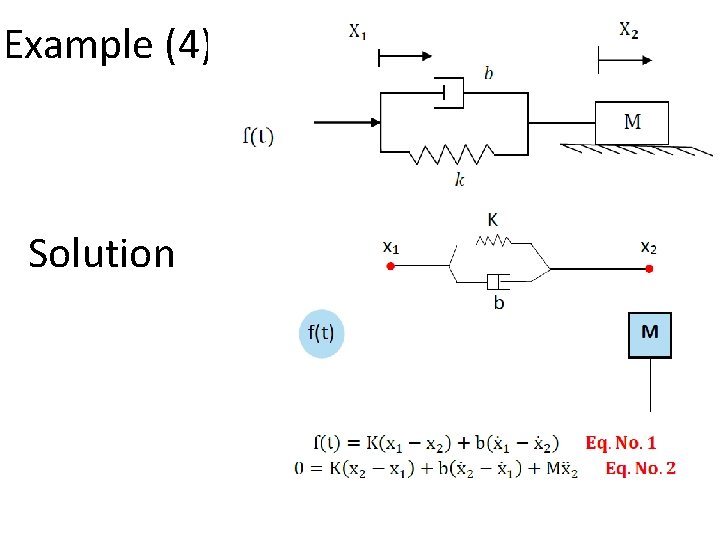
Example (4) Solution

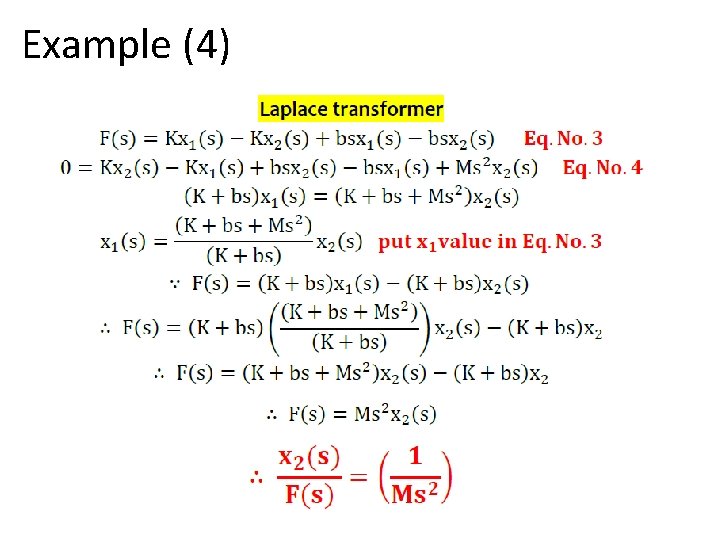
Example (4)

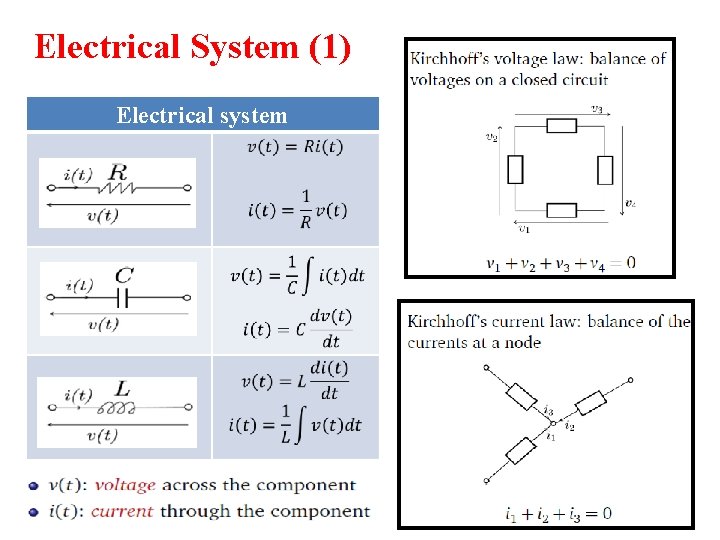
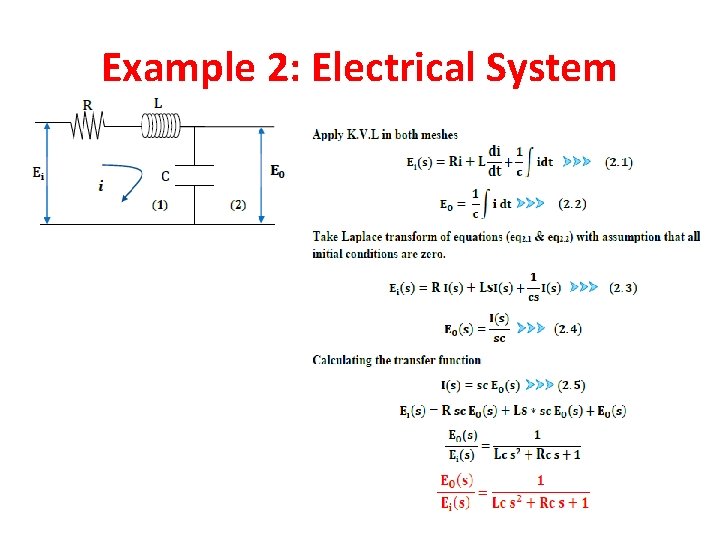
Electrical System (1) Electrical system

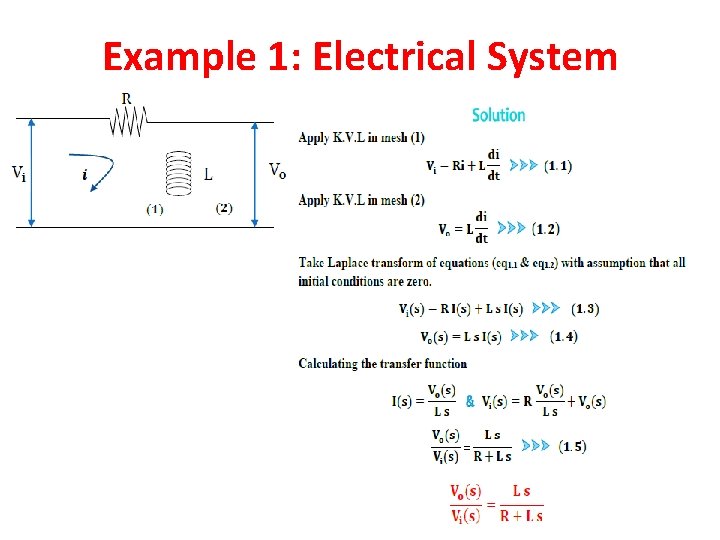
Example 1: Electrical System

Example 2: Electrical System